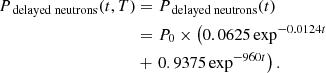| Issue |
EPJ Nuclear Sci. Technol.
Volume 10, 2024
|
|
|---|---|---|
| Article Number | 9 | |
| Number of page(s) | 83 | |
| DOI | https://doi.org/10.1051/epjn/2024010 | |
| Published online | 07 October 2024 | |
https://doi.org/10.1051/epjn/2024010
Regular Article
An introduction to Spent Nuclear Fuel decay heat for Light Water Reactors: a review from the NEA WPNCS
1
Reactor Physics and Thermal hydraulic Laboratory, Paul Scherrer Institut, Villigen, Switzerland
2
Instituto de Fisica Corpuscular, IFIC (CSIC-Univ. Valencia), Valencia, Spain
3
Institute for Nuclear Research (Atomki), H-4001 Debrecen, Hungary
4
CIEMAT – Centro de Investigaciones Energéticas, MedioAmbientales y Tecnològicas, Madrid, Spain
5
Institut de Radioprotection et de Sureté Nucléaire, 92260 Fontenay aux Roses, France
6
EDF, DIPNN-DT, 69007 Lyon, France
7
Universidad Politecnica de Madrid, Madrid, Spain
8
National Nuclear Laboratory, Workington, UK
9
Commissariat à l’énergie atomique et aux énergies alternatives, Cadarache, 13108 Saint-Paul-lez-Durance, France
10
Kernkraftwerk Goesgen-Däniken AG, Däniken, Switzerland
11
Nuclear Transport Solutions (NTS), Risley, UK
12
KIT-Karlruhe Institue of Technology, Karlruhe, Germany
13
Subatech (CNRS/IN2P3, IMT Atlantique, Université de Nantes), 44307 Nantes, France
14
SCK CEN, Belgian Nuclear Research Center, Mol, Belgium
15
Federal Agency for nuclear Control, Brussels, Belgium
16
VTT Technical Research Centre of Finland Ltd., Espoo, Finland
17
Gesellschaft für Anlagen- und Reaktorsicherheit (GRS) gGmbH, Garching bei München, Germany
18
Framatome, Erlangen, Germany
19
Université Paris-Saclay, CEA, Service d’Études des Réacteurs et de Mathématiques Appliquées, 91191, Gif-sur-Yvette, France
20
Oak Ridge National Laboratory, Oak Ridge, TN, USA
21
University of Warsaw, Warsaw, Poland
22
Jožef Stefan Institute, Ljubljana, Slovenia
23
Rolls Royce, Derby, UK
24
EDF – DPNT – DCN – PAD, 93200 Saint Denis, France
25
Orano NC Recycling, 50444 Beaumont Hague, France
26
Orano NPS, 78180 Montigny-le-Bretonneux, France
27
EDF R&D, 91120 Palaiseau, France
28
Division of Nuclear Science and Education, OECD Nuclear Energy Agency (NEA), 75775 Paris, Cedex 16, France
29
AXPO Power AG, Baden, Switzerland
30
Japan Atomic Energy Agency, Ibaraki, Japan
31
Central Research Institute of Electric Power Industry (CRIEPI), Tokyo, Japan
32
Science Engineering Associates S.L. (SEA), Madrid, Spain
33
Sofia University “St. Kliment Ohridski”, Sofia, Bulgaria
34
PreussenElektra GmbH, Hannover, Germany
35
Nagra – Nationale Genossenschaft für die Lagerung radioaktive Abfälle, Wettingen, Switzerland
36
Studsvik Scandpower, Inc., Newton, Massachusetts, USA
37
Swedish Nuclear Fuel and Waste Management Co. (SKB), Sweden, Sweden
38
Dept. of Nuclear Physics, Lund University, Lund, Sweden
39
Uppsala University, Uppsala, Sweden
40
WTI GmbH, Jülich, Germany
* e-mail: dimitri-alexandre.rochman@psi.ch
Received:
9
January
2024
Received in final form:
28
May
2024
Accepted:
2
July
2024
Published online: 7 October 2024
This paper summarized the efforts performed to understand decay heat estimation from existing spent nuclear fuel (SNF), under the auspices of the Working Party on Nuclear Criticality Safety (WPNCS) of the OECD Nuclear Energy Agency. Needs for precise estimations are related to safety, cost, and optimization of SNF handling, storage, and repository. The physical origins of decay heat (a more correct denomination would be decay power) are then introduced, to identify its main contributors (fission products and actinides) and time-dependent evolution. Due to limited absolute prediction capabilities, experimental information is crucial; measurement facilities and methods are then presented, highlighting both their relevance and our need for maintaining the unique current full-scale facility and developing new ones. The third part of this report is dedicated to the computational aspect of the decay heat estimation: calculation methods, codes, and validation. Different approaches and implementations currently exist for these three aspects, directly impacting our capabilities to predict decay heat and to inform decision-makers. Finally, recommendations from the expert community are proposed, potentially guiding future experimental and computational developments. One of the most important outcomes of this work is the consensus among participants on the need to reduce biases and uncertainties for the estimated SNF decay heat. If it is agreed that uncertainties (being one standard deviation) are on average small (less than a few percent), they still substantially impact various applications when one needs to consider up to three standard deviations, thus covering more than 95% of cases. The second main finding is the need of new decay heat measurements and validation for cases corresponding to more modern fuel characteristics: higher initial enrichment, higher average burnup, as well as shorter and longer cooling time. Similar needs exist for fuel types without public experimental data, such as MOX, VVER, or CANDU fuels. A third outcome is related to SNF assemblies for which no direct validation can be performed, representing the vast majority of cases (due to the large number of SNF assemblies currently stored, or too short or too long cooling periods of interest). A few solutions are possible, depending on the application. For the final repository, systematic measurements of quantities related to decay heat can be performed, such as neutron or gamma emission. This would provide indications of the SNF decay heat at the time of encapsulation. For other applications (short- or long-term cooling), the community would benefit from applying consistent and accepted recommendations on calculation methods, for both decay heat and uncertainties. This would improve the understanding of the results and make comparisons easier.
© D. Rochman et al., Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The characterization of Spent Nuclear Fuel (SNF) assemblies is an inherent process of the safety assessment pertaining to the back-end of the nuclear fuel cycle. It concerns the SNF assembly handling and storage, design and operation at reprocessing facilities or final repositories, and is also of prime importance for safeguard and fuel cycle decisions [1]. Many quantities play a key role in such characterization, including the fuel composition, dose, (sub) criticality level, fission gas release, fuel, and cladding behavior, corrosion, material accountability, and decay heat.
The decay heat from nuclear fuel can be defined as the recoverable energy released from the decay of radionuclides during irradiation and after the reactor cycle’s shutdown and corresponds to the released thermal power (historically called decay heat, and more accurately defined today as thermal power). During the operation of a reactor cycle, heat is released in the core mainly from the prompt fission process; the contribution from decay heat is of lesser importance, nevertheless reaching about 7% of the total thermal power in the case of typical Light Water Reactors (LWR) [2], during cycle operation and up to its end. On the contrary, once the reactor cycle is stopped (as part of planned maintenance, reload, or unplanned safety shutdown), the prompt fission heat source dies away and the energy from the decay of fission products, actinides,
activation products and possibly delayed fission becomes the sole heat source. It decreases approximately as a sum of exponentials with different characteristic time parameters as a function of cooling time after the end of the cycle and is emitted at different rates either by assemblies in their end-of-life or by assemblies planned to be used again in following cycles.
Decay heat is a substantial amount of power (being in the order of MW or tens of MW, depending on the reactor core power), and for the next seconds to hours or days (defined as short cooling periods), it can eventually damage the primary and secondary safety barriers if not properly evacuated, resulting in the release of radioactive materials to the environment. Then from days to years of cooling time, the decay heat needs to be taken into account for the SNF handling and wet or dry storage, by having sufficient heat removal capacities. Therefore the design of storage pools, transport casks and surface dry pad storage has to account for this potential hazard. For longer cooling periods, the SNF can be reprocessed or disposed of. In both cases, the decay heat needs to be accounted for. The main influential parameters for its quantification are the following:
-
integral fuel irradiation level, or burnup (in MWd/t), especially important after a long cooling period,
-
initial fuel composition, including its enrichment and initial mass of actinides,
-
cooling time
-
fuel assembly irradiation rate (in MW/t) during the reactor operation, especially important at short cooling times (just after the reactor shutdown or during the fuel unloading for instance),
-
use of burnable poisons (mainly during the first irradiation cycle),
-
other manufacturing and irradiation parameters (such as dimensions, densities, temperatures, and void).
During the past decades, national and international programs were dedicated to studying and understanding the evolution of the SNF decay heat, covering specific ranges for the most relevant parameters, in agreement with the industry standards at that period of exploitation. Such programs included measurements (see Sect. 5), estimations based on different calculation methods (such as summation or standard methods, see Sect. 6), and validation programs (see Sect. 8). For instance, national programs, as in France, provided research and understanding of the long-term behavior of SNF for storage and geological disposal, including decay heat [3], and international collaborations were framed at the Nuclear Energy Agency (NEA) with dedicated meetings and benchmarks, as presented in refences [4–7]. As shown in these studies, before the year 2000, the initial fuel enrichments for UO2 fuel rarely exceeded 3.8% in 235U, with average assembly burnup values generally lower than 55 MWd/kgU. Consequently, measurements and computational efforts were focused on these values and below. Missing are also direct decay heat measurements on MOX assemblies, or also on VVER or CANDU assembly types.
This observation leads to the first justification for developing new efforts toward a re-evaluation of the decay heat prediction capabilities. Since the year 2000, the nuclear fuel design and usage have changed with the evolution of the nuclear industry. The initial enrichment steadily increased until it reached 5.0% in 235U, and the assembly average burnup nowadays extends to 70 MWd/kgU, and occasionally to higher values. Additionally, the use of MOX fuel has increased in some countries, whereas other ones also have it stored from past use. An example is presented in Figure 1 for typical assemblies used before the years 2000 (low enrichment, low burnup, see the curve labeled “case 1”) and 20 years later (higher enrichment, higher burnup, see curves labeled “case 2” and “case 3”).
 |
Fig. 1. Examples of calculated decay heat for typical UO2 assemblies (top), having different burnup and enrichment values; bottom: comparison between typical MOX and UO2 SNF assemblies. |
In the case of UO2 fuel, one can see a significant increase in decay heat between cases 1 and 2, especially for cooling time from 1 to 100 years. This has consequences for the storage of SNF assemblies, as during this period, such assemblies may potentially be moved from one place to another and eventually from cask to canisters, with canisters going into long-term repository. Accordingly, new calculations are needed, implying new validation efforts, hopefully, based on new decay heat measurements. As presented in the same figure (bottom part), the decay heat coming from MOX fuel is also higher than UO2 fuel (in the presented cases, for cooling periods longer than one month). In this case, there are no available direct decay heat measurements at the assembly level, making the validation of calculations with direct measurements unfeasible. These examples illustrate today’s need with respect to the SNF characterization, including among other quantities, nuclide concentrations and decay heat. The precise knowledge of the decay heat for fuel with low and high initial 235U enrichments, low and high burnup values, and short and long cooling times, directly affect the safety and economy of the back-end of the fuel cycle.
The second justification for new efforts in the prediction of SNF decay heat comes from the need for smaller uncertainties and well-assessed biases in measurements and calculations. This stems from stringent safety rules and higher economic constraints. An example of the impact of the knowledge of SNF decay heat concerns the number of required canisters for the final geological disposal. In a simplistic approach, each canister, for instance containing four PWR SNF assemblies, must have a total decay heat value lower than a given limit; high uncertainties or biases on the SNF decay heat values will increase the number of required canisters. Considering that 1% change in the estimation of the SNF decay heat can change the number of required canisters roughly by the same amount, the economical implications of the decay heat knowledge become straightforward.
A third justification for the re-assessment of the SNF decay heat originates from the need for a larger experimental database for validation. As mentioned in Section 5, the majority of measurements for SNF decay heat come from the Clab facility in Sweden, with additionally a limited number of cases from two decommissioned American facilities. Due to their high quality and small uncertainties, the values from the Clab facility represent the current state of the art with respect to measurements and are used for all code validations. While it is a tremendous advantage to be able to access these measurements and all necessary information on the irradiated assemblies, there is an inherent risk in using experimental values coming from a single facility, as possible correlations between measured values are not mitigated with other experimental sources. Additionally, these measurements do not cover all characteristics of today’s SNF assemblies, in terms of initial enrichment, burnup, and fuel type.
In this context, the working group SG12 has been organized under the auspice of the OECD Nuclear Energy Agency (NEA) and the Working Party on Criticality Safety (WPNCS) [8], and is dedicated to “Spent nuclear fuel decay heat: assessing the confidence level in experimental and computational estimations (SNF-DH)”. In order to narrow the field of study of SG12, the primary focus is the existing SNF assemblies from current LWRs, and the main goals of SG12 are as follows:
-
Allowing interested participants to exchange their experience related to the prediction of SNF decay heat (current knowledge, interests, and needs).
-
Provide a state-of-the-art report for the estimation of the decay heat from existing SNF (the present report), including an overview on the calculation capabilities, possible sources of uncertainties and a description of the available experimental data.
-
When applicable, raise awareness for relevant needs, in terms of calculations and measurements.
-
Finally, provide recommendations for improving the SNF decay heat estimation, with respect to measurements, simulations, input information, and best practices.
Such studies are part of other international efforts, such as the International Atomic Energy Agency (IAEA) Coordinated Research Project on Spent Fuel Characterization (running from 2020 to 2024), as well as the European Union joint Strategic Programme of Research and knowledge management activities, dedicated to supporting radioactive waste management studies, called EURAD (running from 2019 to 2024). Another important international project concerns the measurements and the evaluations of decay heat at Clab, Sweden, between SKB, Vattenfall, and EPRI. When completed, one of the outcomes of this project will be the measured decay heat for a number of new SNF assemblies as well as the necessary information to perform decay heat calculations.
2. Motivation
As mentioned in the introduction, the estimation of the SNF decay heat is important at various cooling periods, from seconds after a reactor shutdown, up to millions of years later for the safety case of geological repositories. Our capability to calculate this quantity (linked to other ones such as nuclide inventory), as well as to provide well-justified uncertainties and biases has direct implications on the simulations of accident scenarios, as well on the safety of the back-end of the fuel cycle, and naturally on involved cost. Our ability to excel in such estimations, and to improve safety and cost are the main motivations for presenting the state of the art from the aspects of measurement, simulation, and validation.
The availability of a limited number of measurements for SNF decay heat is directly affecting the confidence level of simulations. Such experiments are expensive and currently only one facility exists worldwide. The domain of validation is therefore restrained, potentially leading to increased safety margins. Raising awareness of the need for new and independent measurements is consequently the first priority of this work.
Understanding and informing about the different possibilities in simulations and the impact of different parameters is the second priority. Various methods, guidelines, and recommendations exist among institutes and countries, leading to different calculated decay heat values, even when starting from the same measurement database. Such variations of results should be made visible and explained to specialists and non-specialists.
Both previous points directly affect validation results. The scarcity of experimental values, as well as different simulation methods, may lead to different consequences for the outcome of a validation procedure (such as safety factors, confidence intervals, or uncertainties). Additionally, different validation procedures can also have different impacts on application quantities. Again, making such differences explicit, and understanding them is the third priority of this work.
Additional details are given in the following paragraphs, articulated around these three axes: measurements, simulations and validation.
2.1. General observations on current knowledge
Validation of the existing codes with measured SNF decay heat is currently considered a necessity by most existing national and international regulations (see for instance the IAEA Safety Guide Refs. [9, 10]). Part of the motivation to continue performing analysis and measurements for SNF decay heat is due to today’s trend of increasing burnup and initial enrichment values, and also due to the need to improve current predictions. To illustrate our current capabilities for predictions, Figure 2 represents one aspect of the validation of codes used in the calculations of SNF decay heat.
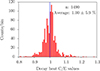 |
Fig. 2. Histogram of the ratios of calculated (C) over experimental (E) decay heat values from literature studies for calorimetric measurements of full fuel assemblies. Both PWR and BWR assemblies are included. |
This figure presents the histogram for C/E ratios (being Calculated over Experimental values) for SNF decay heat coming from calorimetric studies. All (tabulated) values from the open literature are used for this figure, mixing PWR and BWR assemblies, different simulation codes, nuclear data libraries, calculation procedures, and experimental sources. Such results do not represent the outcome of a validated procedure, but rather a snapshot on the existing published data. In total, 1490 calculated over experimental ratios were found, and the average of such histogram is 1.003, with a standard deviation of 0.059. Such figures indicate at first sight that the simulation capabilities can satisfactory reproduce measured decay values for SNF with calorimetric measurements. One standard deviation is found to be close to 6%, and almost 86% of the data are within ±1σ. By considering two standard deviations, almost 97% of the cases are covered; a three-sigma interval leads to 98.8% of the cases (five sigmas cover 99.6%). Numbers are changing if ones differentiate between PWR and BWR SNF assemblies, as indicated in Table 1.
Calculated over experimental ratios for LWR SNF assemblies (average and 1 standard deviation).
As observed in previous work, the spread of C/E is larger for BWR than for PWR. This is certainly linked to the fact that BWR cases are more challenging to simulate, for instance, due to the heterogeneity of the irradiation conditions (such as radial and axial void variations). Depending on the application, such numbers can be considered as adequate or not. It is nevertheless important to understand the limitations of the experimental database used to perform such validation. In some cases, considering one standard deviation is not enough, as too many cases are left outside the ±1σ band. Table 2 is presenting the number of C/E cases (from Tab. 1) which are included in various multipliers of ±σ.
It can be seen that if a specific application requires that more than 99% of the cases are covered, one needs to consider 3σ for the PWR SNF assemblies (corresponding to 1.000 ± 0.138), and 5σ for the BWR SNF assemblies (corresponding to almost 1.009 ± 0.395). Such large uncertainties, in terms of standard deviations, can have important consequences on facility designs, and it is therefore of high interest to improve the prediction capabilities.
Another quantity of high interest is the average value presented in Table 1. It can be defined as an average simulation bias, which is for instance of less than 2% in the case of the PWR SNF assemblies. The mentioned references are based on calculations performed with available measured SNF cases, implying a strong correlation between the presented values. More recently, a blind benchmark performed with 5 PWR SNF assemblies at the Clab facility, with more than 30 participants, has indicated an average bias of 0.978 (± 0.022) [15]. Later re-analysis of the experimental values (as of mid-2023) indicates an overestimation of the measurements, but such original value based on a blind exercise is in disagreement with the average values from Table 1. It is indicating that a more adequate understanding of possible bias sources is required.
2.2. Limitations
The main impediment to the results presented in the previous section lies in the limits of the application of the existing experimental database. Such validation (average C/E values and standard deviations) is based on a very limited set of measurements:
-
Three facilities worldwide delivered 268 publicly available measurements for 164 SNF assemblies, up to the year 2006 (see for instance lists in Refs. [13, 14])1. See Tables 11 and 12 for details,
-
among these three facilities, two do not exist nowadays (GE-Morris and HEDL-EMAD),
-
out of 268 measurements, more than 50% come from the Swedish Clab facility and 40% from the American GE-Morris facility (currently shutdown),
-
only UO2 SNF assemblies for PWR and BWR were measured (no MOX fuel, no other design such as for VVER),
-
the highest enrichment is 4%, which is lower than the ones typically used in current reactors,
-
the highest assembly average burnup is 51 MWd/kgU, which is also lower than the values reached in current reactors,
-
the cooling time ranges from 2 to 27 years, which does not cover all cooling ranges of interest.
As mentioned, the estimation of decay heat is relevant for fuel management over a large period of cooling periods: short (e.g. for Loss Of Coolant Accident or Reactivity Insertion Accident), intermediate (for on-site SNF storage) and long (for off-site storage or disposal such as deep geological repository); some general information related to such needs is provided in the following section.
2.3. Needs
Note that the influential parameters (see the bullet list in the introduction) do not have the same weight depending on whether one considers the SNF just after the reactor shutdown or after a long cooling period in the SNF pool.
2.3.1. Decay heat for short cooling times
A conservative evaluation of decay heat is paramount for the proper design of heat removal systems of nuclear power plants (for an adequate mitigation of loss of coolant accidents for instance). The typical period of interest in safety studies goes from the reactor shutdown to about ten days. The number of contributing radionuclides is well over a thousand just after the reactor shutdown, and that number decreases rapidly, as presented in Figure 3 reproduced from reference [16].
 |
Fig. 3. Number of nuclides that have to be computed to obtain a fraction (99%, 99.9%,..., 100% – ϵ, with ϵ = 10−12%) of the total decay heat computed by DARWIN with the JEFF-3.0 nuclear data library. Left: short cooling time in seconds from 0.1 to 1013 seconds. Right: long cooling time in days from 1 day to 1011 years. |
During this short cooling time period, the decay heat is nearly proportional to the reactor power before the reactor shutdown (“thumb rule” to be used with caution), as most of the contributing radionuclides are short-lived. For the same reason, it depends less on fuel burnup.
2.3.2. Decay heat for intermediate cooling times
In the 5 to 25-day period after reactor shutdown, the main application of decay heat evaluation is the safe unloading of the core into the nearby pool. Systems must take into account penalized values to cover fuel variability in power and irradiation during the fuel transfer. In case of suspected fuel leakage, the assembly decay heat must be lower than a given threshold to enable a vacuum-canister sipping procedure. In this intermediate period, the decay heat is still strongly linked to the assembly power before the reactor shutdown. However, the irradiation level has an increasing influence on cooling time.
Safety systems must be able to remove the decay heat of the complete unloaded core added to one of the fuel assemblies already stored in the pool. Once the fuel is partially reloaded back into the core, the safety systems still have to remove the decay heat from the definitively unloaded assembly batch and the fuel already stored in the pool.
2.3.3. Decay heat for long cooling times
Long cooling times correspond to fuel assemblies that have cooled down several months or years. Typical needs for decay heat evaluation are:
-
Design of spent fuel pool heat exchangers,
-
design of canisters and cylinders for fuel managing and fuel storage,
-
design of casks for fuel transport,
-
verification of fuel compliance with the heat thresholds of the mentioned containers.
The decay heat for long cooling times is not very sensitive to the fuel power before shutdown. It is mainly dependent on fuel burnup. Other decay heat evaluation needs for long cooling times are related to fuel reprocessing, radioactive material vitrification and naturally radioactive waste storage or repository. As mentioned in the introduction, the estimation of the SNF decay heat is important at various cooling periods, from seconds after a reactor shutdown, up to millions of years later for the safety case of geological repositories. Our capability to calculate this quantity (linked to other ones such as nuclide inventory), as well as to provide well-justified uncertainties and biases has direct implications on the simulations of accident scenarios, as well on the safety of the back-end of the fuel cycle, and naturally on involved cost. Our ability to excel in such estimations, and to improve safety and cost are the main motivations for presenting the state of the art from the aspects of measurement, simulation and validation.
The availability of a limited number of measurements for SNF decay heat is directly affecting the confidence level of simulations. Such experiments are expensive and currently only one facility exists worldwide. The domain of validation is therefore restrained, potentially leading to increased safety margins. Raising awareness on the need of new and independent measurements is consequently the first priority of this work.
Understanding and informing about the different possibilities in simulations and the impact of different parameters is the second priority. Various methods, guidelines and recommendations exist among institutes and countries, leading to different calculated decay heat values, even when starting from the same measurement database. Such variation of results should be made visible and explained for specialists and non specialists.
Both previous points directly affect validation results. The scarcity of experimental values, as well as different simulation methods may lead to different consequences for the outcome of a validation procedure (such as safety factors, confidence intervals or uncertainties). Additionally, different validation procedures can also have different impacts on application quantities. Again, making such differences explicit, and understanding them is the third priority of this work.
Additional details are given in the following paragraphs, articulated around these three axes: measurements, simulations, and validation.
2.4. General observations on current knowledge
Validation of the existing codes with measured SNF decay heat is currently considered as a necessity by most of existing national and international regulations (see for instance the IAEA Safety guide Refs. [9, 10]). Part of the motivation to continue performing analysis and measurements for SNF decay heat is due to today’s trend of increasing burnup and initial enrichment values, and also due to the need in improving current predictions. To illustrate our current capabilities for predictions, Figure 2 represents one aspect of the validation of codes used in the calculations of SNF decay heat.
This figure presents the histogram for C/E ratios (being Calculated over Experimental values) for SNF decay heat coming from calorimetric studies. All (tabulated) values from the open literature are used for this figure, mixing PWR and BWR assemblies, different simulation codes, nuclear data libraries, calculation procedures, and experimental sources. Such results do not represent the outcome of a validated procedure, but rather a snapshot of the existing published data. In total, 1490 calculated over experimental ratios were found, and the average of such histogram is 1.003, with a standard deviation of 0.059. Such figures indicate at first sight that the simulation capabilities can satisfactorily reproduce measured decay values for SNF with calorimetric measurements. One standard deviation is found to be close to 6%, and almost 86% of the data are within ±1σ. By considering two standard deviations, almost 97% of the cases are covered; a three-sigmas interval leads to 98.8% of the cases (five sigmas cover 99.6%). Numbers are changing if ones differentiate between PWR and BWR SNF assemblies, as indicated in Table 1.
As observed in previous work, the spread of C/E is larger for BWR than for PWR. This is certainly linked to the fact that BWR cases are more challenging to simulate, for instance due to the heterogeneity of the irradiation conditions (such as radial and axial void variations). Depending on the application, such numbers can be considered adequate or not. It is nevertheless important to understand the limitations of the experimental database used to perform such validation. In some cases, considering one standard deviation is not enough, as too many cases are left outside the ±1σ band. Table 2 is presents the number of C/E cases (from Tab. 1) which are included in various multipliers of ±σ.
It can be seen that if a specific application requires that more than 99% of the cases are covered, one needs to consider 3σ for the PWR SNF assemblies (corresponding to 1.000 ± 0.138), and 5σ for the BWR SNF assemblies (corresponding to almost 1.009 ± 0.395). Such large uncertainties, in terms of standard deviations, can have important consequences on facility designs, and it is therefore of high interest to improve the prediction capabilities.
Another quantity of high interest is the average value presented in Table 1. It can be defined as an average simulation bias, which is for instance less than 2% in the case of the PWR SNF assemblies. The mentioned references are based on calculations performed with available measured SNF cases, implying a strong correlation between the presented values. More recently, a blind benchmark performed with 5 PWR SNF assemblies at the Clab facility, with more than 30 participants, has indicated an average bias of 0.978 (± 0.022) [15]. Later re-analysis of the experimental values (as of mid 2023) indicates an over estimation of the measurements, but such original value based on a blind exercise is in disagreement with the average values from Table 1. It is indicating that a more adequate understanding of possible bias sources is required.
2.5. Limitations
The main impediment of the results presented in the previous section lies in the limits of application of the existing experimental database. Such validation (average C/E values and standard deviations) is based on a very limited set of measurements:
-
Three facilities worldwide delivered 268 publicly available measurements for 164 SNF assemblies, up to the year 2006 (see for instance lists in Refs. [13, 14])2. See Tables 11 and 12 for details,
-
among these three facilities, two do not exist nowadays (GE-Morris and HEDL-EMAD),
-
out of 268 measurements, more than 50% come from the Swedish Clab facility and 40% from the American GE-Morris facility (currently shutdown),
-
only UO2 SNF assemblies for PWR and BWR were measured (no MOX fuel, no other design such as for VVER),
-
the highest enrichment is 4%, which is lower than the ones typically used in current reactors,
-
the highest assembly average burnup is 51 MWd/kgU, which is also lower than the values reached in current reactors,
-
the cooling time ranges from 2 to 27 years, which does not cover all cooling ranges of interest.
As mentioned, the estimation of decay heat is relevant for fuel management over a large period of cooling periods: short (e.g. for Loss Of Coolant Accident or Reactivity Insertion Accident), intermediate (for on-site SNF storage), and long (for off-site storage or disposal such as deep geological repository); some general information related to such needs is provided in the following section.
2.6. Needs
Note that the influential parameters (see the bullet list in the introduction) do not have the same weight depending on whether one considers the SNF just after the reactor shutdown or after a long cooling period in the SNF pool.
2.6.1. Decay heat for short cooling times
A conservative evaluation of decay heat is paramount for the proper design of heat removal systems of nuclear power plants (for an adequate mitigation of loss of coolant accidents for instance). The typical period of interest in safety studies goes from the reactor shutdown to about ten days. The number of contributing radionuclides is well over thousand just after the reactor shutdown, and that number decreases rapidly, as presented in Figure 3 reproduced from reference [16].
During this short cooling time period, the decay heat is nearly proportional to the reactor power before the reactor shutdown (“thumb rule” to be used with caution), as most of the contributing radionuclides are short-lived. For the same reason, it depends less on fuel burnup.
2.6.2. Decay heat for intermediate cooling times
In the 5 to 25 days period after reactor shutdown, the main application of decay heat evaluation is the safe unloading of the core into the nearby pool. Systems must take in account penalized values to cover fuel variability in power and irradiation during the fuel transfer. In case of suspected fuel leakage, the assembly decay heat must be lower than a given threshold to enable a vacuum-canister sipping procedure. In this intermediate period, the decay heat is still strongly linked to the assembly power before reactor shutdown. However, the irradiation level has an increasing influence with cooling time.
Safety systems must be able to remove the decay heat of the complete unloaded core added to the one of the fuel assemblies already stored in the pool. Once the fuel is partially reloaded back into the core, the safety systems still have to remove the decay heat from the definitively unloaded assembly batch and the fuel already stored in the pool.
2.6.3. Decay heat for long cooling times
Long cooling times correspond to fuel assemblies that have cooled down several months or years. Typical needs for decay heat evaluation are:
-
design of spent fuel pool heat exchangers,
-
design of canisters and cylinders for fuel management and fuel storage,
-
design of casks for fuel transport,
-
verification of fuel compliance with the heat thresholds of the mentioned containers.
The decay heat for long cooling times is not very sensitive to the fuel power before shutdown. It is mainly dependent on fuel burnup. Other decay heat evaluation needs for long cooling times are related to fuel reprocessing, radioactive material vitrification, and naturally radioactive waste storage or repository.
3. Definition
In the following, the meaning of a number of quantities related to decay heat is explained. Even though the level of details can be appreciably extended, a minimum amount of information is provided in the following, allowing the reader to understand each term, and possibly to explore mentioned citations for additional details.
3.1. Spent nuclear fuel
In the present context, several complementary definitions of “Spent Nuclear Fuel” assembly (or simply SNF) can be used:
-
SNF, also called spent fuel or depleted fuel, is a nuclear fuel that has been irradiated in a nuclear reactor (usually at a nuclear power plant or an experimental reactor) and that may be replaced by fresh fuel if it can no longer sustain fission in that environment due to physical, regulatory/licensing or economical limitations. Nuclear fuel becomes spent when its fissionable nuclides have been partially consumed and fission-product poisons have accumulated in it. SNF is characterized by its burnup (see Sect. 3.5) which is a measure of its utilization level.
-
SNF is a nuclear fuel withdrawn from a nuclear reactor following irradiation. SNF has not been chemically separated from its constituent elements by reprocessing: it includes the special nuclear material, by-product material, source material, and other radioactive materials associated with fuel assemblies.
SNF can also be called “Used Nuclear Fuel” (or UNF) and both terms are often interchangeable. They nevertheless do not refer to the same views, as the term SNF implies the concept of waste to be disposed of, whereas UNF suggests a possible reuse. Different institutions use either terms (NRC [17], IAEA [18], NWMO [19]), or a mix of both (US DOE). In this document, SNF is used with the broader meaning “nuclear fuel that has been irradiated in a nuclear reactor”.
3.2. Spent nuclear fuel characterization
Decay heat is one of the most important quantities for SNF characterization (or SFC for Spent Fuel Characterization). There is not a unique definition for the SFC, and one can refer to the ASTM C 1682:21 Standard Guide for Characterization of Spent Nuclear Fuel in Support of Interim Storage, Transportation, and Geologic Repository Disposal [20], which guides testing (involved in characterizing the physical and chemical nature of SNF) in support of its interim storage, transport, and disposal in a geologic repository. In this context, the experimental and computational characterization efforts can be defined as:
Any test conducted principally to furnish information for a mechanistic understanding of alteration (for example, electrochemical polarization tests, leach tests, solubility tests, etc)
where the “alteration” is defined as any change to the form, state, or properties of the material under consideration. A non-exhaustive list of possible test fields is given below:
-
Physical appearance, Extent, and distribution of visible cladding damage
-
Weight/size/dimensions of SNF assemblies
-
Radionuclide and fissile content
-
Criticality-safety
-
Metallography/optical microscopy
-
Water content and drying characteristics
-
Oxidation kinetics
-
Ignition characteristics
-
Dissolution characteristics
-
Deliquescence and advective flow.
One of the challenging aspects of the SFC is the change of the SNF characteristics as a function of cooling time. Several experimental tests can be done at a certain time, and they need to be combined with theoretical models to understand the long-term evolution of given observables. Typical examples concern the change in the nuclide concentrations (due to natural decay), or in oxidation, directly affecting criticality values for hundreds of thousands of years.
Understanding the characteristics of SNF is essential in all spent fuel management activities, the SFC being a prerequisite for such safe and economical management. The IAEA Joint Convention on the Safety of Spent Fuel Management and the Safety of Radioactive Waste Management in 1997 defines spent fuel management as follows [21]:
“spent fuel management” means all activities that relate to the handling or storage of spent fuel, excluding off-site transportation.
One can also note that the important characteristics in spent fuel management mainly depend on the evaluated quantities. Important characteristics for criticality-safety in spent fuel pools may differ from those important in transport, dry storage, or final disposal repository.
3.3. Decay heat
The term “decay heat”, generally expressing the recoverable energy generated by the decay of nuclides from nuclear fuel, does not correspond to the correct modern terminology. The term heat is nowadays used to describe energy transfer, for instance, based on the mechanism of conduction or radiation (without the transfer of matter). As an energy, the proper unit of heat is Joule, or sometimes calorie. A better designation is “decay power”, therefore correctly expressed in Watts, or eventually in Watt per ton (of matter). As the term “decay heat” was historically used from the 1940s, it is still employed today, with the understanding that the quantity of interest is expressed in Watt.
The term “thermal power” (or “residual thermal power”) is also sometimes used (as in the DIN standard [22]), although the word “thermal” refers to the power generated in the reactor core, commonly called thermal power (to differentiate it from the electrical power). Specific definitions can be found in different guides or countries:
-
US DOE: it is considered that decay heat is a particular problem associated with nuclear reactors. Even though the reactor is shut down, heat is produced from the decay of fission fragments (note that this definition does not include the contribution from actinides). Limits for each particular reactor are established to prevent damage to fuel assemblies due to decay heat [23]. This reference provides two definitions of decay heat generation rate. The first definition is related to the physical process of decay heat generation as a result of a fission reaction and obtained products that contain excess energy. The second definition is related to the energy excess in the form of heat, which appears to be a safety feature. There should be established limits, based on the engineering design, not to be exceeded. Therefore, the decay heat generation rate is not only a physics feature but also an engineering concept.
-
US NRC: the heat produced by the decay of radioactive fission products after a reactor has been shut down (March 2021). As mentioned, it should be noted that such a definition does not include the contribution of actinides.
-
US NRC Regulatory guide 3.54, revision 2: the heat generation rate of the spent fuel assembly is the recoverable thermal energy (from radioactive decay) of the assembly per unit of time and per unit of fuel mass. Heat generation rate has also been referred to as decay heat rate, afterheat, or afterheat power.
-
ASN, (France, not translated to avoid modifications): La puissance résiduelle est la puissance thermique développée par un réacteur nucléaire après l’arrêt, provenant essentiellement de la radioactivité du combustible nucléaire et des autres matériaux ainsi que des fissions résiduelles.
-
According to the ISO standard of 1992 [24], “The decay heat power of nuclear fuels is the thermal power produced by radioactive decay of fission and activation products of the nuclear fuel following the shutdown of a nuclear reactor” (note that the contribution from actinides is also missing).
-
In the German DIN standard [22, 25], the decay power is defined as the “thermal power generated by the decay of nuclides in the nuclear fuel”.
It should be noted that if these definitions differ in their formulation and on some specific points, they all agree on the physical phenomenon: released energy from the nuclear components and other materials after the reactor shutdown (although many definitions do not include the contribution from actinides, and one can consider as well that the decay heat is also produced during a reactor cycle).
3.4. Decay heat standards
Standard methods and reference guides for the calculation of SNF decay heat have been established in different countries; details can be found in Section 6.3. They provide acceptable procedures for calculating such decay heat (mathematical methods, range of applications, and often examples), which sensibly differ from the summation method (see Sect. 6.4.1). The main advantages of these methods are that they can be applied given a limited set of parameters representing the SNF and its irradiation, such as average burnup, cooling time, initial enrichment, and partial fission contributions from the main actinides. They do not necessitate neutron transport and fuel depletion calculations and can provide values a short calculation time. Examples of such methods are the ANS-5.1 [26], ISO [27], NRC-3.54 [28], and the DIN 25463-1 [22] standards.
3.5. Burn up (or burnup)
The burnup is a measure (not in the experimental meaning) of the utilization level of the fuel. Depending on the perspective of the final user, different approaches are commonly encountered to quantify the burnup. One of them reflects the number of fissions that have taken place:
-
It can be expressed as the fission density, i.e. the number of fissions in a given volume. Units such as fiss./cm3 or fiss./m3 are commonly used in the research reactor community; those are simply obtained by integrating, over time, the fission rate, itself being the product of neutron flux with the fuel macroscopic fission cross-section.
-
It may also be described as the relative fraction of actinides that has fissioned. Radiochemists often use the term “Fissions per Initial Heavy Metal Atom”, or FIMA, unit in spent fuel assays, before converting that to more practical units for the end-users.
However, by far, the most common approach to commercial fuel burnup is to describe its specific thermal energy output. Indeed, for commercial reactor operations, the total thermal core power is known through the thermal balance at the core inlet and outlet. Integrated over time for a given cycle, one obtains the cycle thermal energy generation, which translates into the cycle performance. That latter quantity is often characterized by the number of effective full-power days i.e., the equivalent number of days at nominal power corresponding to the cycle thermal energy output. The relative distribution of fissions and, hence, the nominal power in the core is known from core physics calculations and/or from in-core instrumentation.
The product of the fuel assembly nominal power, for example in MW, with the number of effective full-power days enables a fast evaluation of the thermal power output of each assembly, as well as its specific thermal output if divided by the fuel mass or by the initial heavy-metal mass. The natural units to express the burnup level for commercial reactors are therefore MWd/kgHM, or variants involving GW or tHM (HM refers to Heavy Metals). Those units are also often used from licensing and/or regulatory perspectives.
An equivalence, or conversion factors, between those units, can easily be established if one assumes an effective energy release of 200 MeV per fission event and a density of 10 960 kg/m3 for UO2 fuel:
As presented in reference [29], “fuel burnup measures how much energy is extracted from nuclear fuel and is a measure of fuel depletion.”.
As a simple representative example of this quantity, it can be considered that the fission of a single nucleus of 235U induced by a thermal neutron releases about 200 MeV of recoverable energy. To produce 1 Watts of power, a total of 3.1 × 1010 fissions per second is needed. To reach an energy (or burnup) of 1 MWd (megawatt-day), one needs about 2.5 × 1021 fissions. If every nucleus undergoes fission, the same amount of nuclei is necessary, which is roughly contained in 1 gram of any fissile material.
It is important to note that this relation between burnup and the number of fissions is only a rough approximation. The average recoverable energy per fission depends on the fissioned nuclide as well as on the contribution from other, non-fission, neutron-induced reactions, which depends also on system design and operational parameters. The actual value may vary by up to about 5%. In addition to these definitions, the following distinctions are often useful:
-
Core burnup: averaged burnup over entire core (for all fuel assemblies).
-
Assembly burnup: averaged burnup over a single fuel assembly.
-
Assembly node burnup: average burnup value for a vertical segment of an assembly. A vertical segment usually represents 10 cm to 20 cm.
-
Pin burnup: averaged burnup over a single fuel pin or fuel rod.
-
Local burnup: burnup values within a single fuel pellet.
The assembly burnup is one of the most important quantities for the determination of the assembly decay heat. It can unfortunately not be directly measured and is either calculated or derived from the measurements of related quantities. Due to its importance for the estimation of assembly decay heat, some general information is provided hereafter. Details can be found for instance in references [30, 31].
3.5.1. Calculated burnup
As indicated in the following, the assembly burnup can be calculated by performing a full-core calculation (such as in core follow-up calculations), or part of the rod burnup can be assessed with a single-assembly calculation (such as during lattice code validation). The second one still depends on the information provided by the core simulator, implying that the knowledge of the calculated assembly burnup cannot be better than the performance of the core simulator. Biases and uncertainties for the calculated burnup should not be assumed negligible.
From lattice code
Lattice codes are often used for the calculation of nuclide concentrations in specific samples obtained from irradiated rods or assemblies (in Post Irradiation Examination, or PIE). Such calculations are of importance as they are often used in code validation (see Sect. 8), which may eventually impact the conditions of SNF transport and storage. These calculated concentrations are then compared to measured ones, for instance for samples contained in the SFCOMPO database [32]. In such lattice calculations, the sample burnup is first obtained based on core simulator data (see next paragraph). The accepted practice is that to compensate for the lack of knowledge of the full irradiation conditions, the sample burnup can be modified so that the calculated concentration of a specific nuclide matches its measured value, for instance for a burnup indicator, such as 148Nd.
In this approach, the sample burnup value cannot be known better than the concentration uncertainty of the selected nuclides (varying from tens of a percent, up to 5%). Such sample value is of course different from assembly burnup, and the extrapolation is not straightforward, due to the normalization effect to a measured nuclide concentration, and to the axial and radial burnup distributions. An example of the radial burnup distribution is presented in Figure 4 for the ARIANE sample GU3 [33].
 |
Fig. 4. Comparison between the CASMO5 (single-assembly calculation, left) and SIMULATE (full-core calculation right) pin burnup values for the GU3 sample. The sample location is indicated with an orange square [33]. |
On the left is a lattice calculation performed with the code CASMO5, assuming reflective boundaries outside the assembly of interest (usually, no information for the neighboring assemblies is provided for PIE analysis). Consequently, there is a symmetry for the burnup distribution of the concerned segment. On the right is the calculated burnup distribution from the code SIMULATE, considering the realistic assemblies surrounding the assembly of interest. It can be observed that the two burnup distributions are different, illustrating the burnup simplification obtained in lattice calculations.
Example of single assembly burnup calculations for a UO2 and a MOX assembly. Both are initially enriched at 4% in fissile materials. Calculations are performed with CASMO5. “Fis.” corresponds to the fissile nuclides and “Fer.” to the fertile nuclides.
Concerning the normalization of the lattice calculation to the measured concentration of burnup indicators (148Nd, 137Cs, or a few Nd isotopes), helps assess solely the effect of a specific code, its nuclear data library and the modeling method, based on irradiation parameters (usually) provided by a core simulator. The normalization removes the effect observed on the right side of Figure 4 (neighboring assemblies). But it also does not allow to disentangle fission contributors (such as 235U and 239Pu, as their productions of 148Nd are roughly equivalent); the power history (and the sample burnup) can consequently be incorrect, even if the agreement with specific nuclide concentrations is acceptable. A way to bypass this issue is to normalize the power history to match the ratio of measured nuclides concentrations which are differently produced from 235U and 239Pu, such as 90Sr over 150Nd [34] (different fission yields for the two main fission contributors can help to better assess if individual contributions are correctly captured during the simulation).
From core simulator
The assembly burnup, as well as the assembly node burnup profile, can be calculated based on various in-core detectors (e.g. fission chambers), measured core thermal output (based on temperature and flow measurements), and validated core simulator. Alternatively, the methods to calculate the assembly burnup may vary from one code to another, and have evolved over time (a possible consequence is a change of attributed assembly burnup over time).
Because the estimation of the burnup often relies on core simulators for the vast majority of burned assemblies, the decay heat of such SNF can be directly affected by the burnup values obtained from such simulations. A recent analysis of the possible errors in assembly reactivity, based on in-core measurements can be found in reference [35]. Such analysis provides an estimated error in assembly reactivity as a function of the assembly node burnup, using in-core flux map measurements for different PWR cores. The method is based on varying assembly burnup values and calculating the impact on the comparison between the measured and calculated power maps. The impact of such variations is compared to the nominal values (best estimate burnup values) and possible biases are derived. The conclusion of this study mainly concerns the reactivity biases at hot full power (HFP) and cold conditions. Assembly burnup values were modified by a factor between 0.85 and 1.15, but a agreement between calculated and measured in-core flux was found with factors generally within ±5%.
Although a detailed study should be performed to analyze the distribution of such factors (not available from the mentioned reference), this study indicates that a certain degree of freedom exists for the estimation of the assembly burnup, probably within the range of a few percent.
3.5.2. Example of calculated burnup
As presented earlier, a very simple calculation indicates that the fission of all nuclei contained in 1 gram of fissile material provides about 1 MWd. This is naturally a simplification, as other reactions happen in the fuel, due to the mixture of initial nuclides (235U and 238U, and in some cases Pu isotopes), and the build-up of fission products. Neutron capture on actinide nuclides and fission products also produces energy, which modifies the simple previous account. Two examples of calculated burnup values from realistic assemblies are presented in Table 3: one UO2 and one MOX assembly, both initially enriched at 4% in fissile materials. These examples were obtained from lattice calculation (single assembly) with the code CASMO5.
One can then observe that for realistic assemblies and irradiation conditions, more than one nuclide contributes to the total released energy. Modern depletion codes can consider the contribution from different nuclides and provide relatively precise burnup values. Naturally, the underlying nuclear data used for these calculations (Q-values, energy release as a function of the neutron energy, fission and capture cross sections) are not perfectly known, which can modify the calculated assembly burnup. As previously mentioned, changes in an assembly burnup value directly affect the assembly decay heat.
As a last example of calculated burnup, the case of burnup values from core simulators is considered in the following. For a realistic PWR cycle, two different calculations are performed with the same core simulation code, but different versions (nonetheless the same nuclear data library), called in the following V1 and V2. Often, a new code version implies an additional update in the input file for the cycle description, and the input file was therefore modified. Both calculations were validated against in-core data and showed similar performances. There were nevertheless changes in the calculated burnup values, both for assembly average and pin-wise values, and differences in percent are presented in Figure 5.
 |
Fig. 5. Burnup differences for assembly and pin values, for a realistic cycle calculation, from two different versions of the same core simulator. |
As observed, the changes for the average assembly burnup are within ±2%, with higher deviations at low burnup. The pin burnup values present a larger spread. This is an indication that the assembly burnup values from a core simulator are not uniquely defined, and a certain amount of uncertainty is also propagated to decay heat values.
3.5.3. Measured burnup
The term “measured burnup” is by itself not correct, as burnup or fissile content values are not directly measured, but can be derived from other measured quantities combined with specific calculations and assumptions. Such measurements concern the neutron and gamma radiations emitted from an assembly. The build-up of minor actinides during the depletion of the assembly leads to the emission of a number of α particles due to the relatively short half-life of such nuclides (e.g. isotopes of Am, Cm). The rate of α emission is generally high enough to produce a significant amount of neutrons and gamma rays from (α,n) reactions and spontaneous fission. A strong dependence between the neutron emission rate and the burnup exits can be used to infer the assembly’s average burnup [36]. In practice, complications can arise as the measurements of gamma-ray spectra represent a mixture of fission products, activation products, and actinides that have built up during the assembly irradiation.
Different techniques exist to measure gamma-ray or neutron emissions (see for instance Ref. [37]). In active neutron detection, an external neutron source is used, consequently increasing the neutron flux from neutron-induced fission events occurring in the residual fissile material; the time dependence of the neutron count rate is used to infer the quantify the amount of fissile material. In the case of gamma-ray measurements, specific gamma-ray energies are measured, corresponding to the decay of well-known fission products. Such fission products need to be produced in significant amounts (high fission yield), having a half-life long enough to allow gamma-ray measurements, and gamma-ray energies which are easy to identify. 137Cs is consequently a good candidate (half-life of 30.07 years, with a gamma-ray energy of 661.7 keV), being the main gamma-ray emitter after a few years of cooling time. During this type of measurement, background subtraction can be significant, implying long counting times to reach adequate statistical accuracy. Details can be found in Section 5.2.2 and in Appendix C. A third method used to experimentally infer the assembly burnup is the passive neutron measurement technique. It consists in detecting emitted neutrons from spontaneous fission of minor actinides, mainly from 244Cm, with a half-life of 18.1 years. 244Cm emits more than 90% of the neutrons from an irradiated assembly for cooling times ranging from 10 years to 100 years. Its concentration is highly sensitive to the assembly burnup, but also measurement factors (such as detector positioning). Additionally, the SNF irradiation conditions need to be well known to correctly calculate the concentration of 244Cm.
4. Physical origin of decay heat, key contributors
The complexity of the decay heat process originates from the fact that one handles with byproducts of radioactive decay, which can be understood from the quantum mechanics theory. In particular, one refers to the internal energy levels of the nuclei. As the density of those levels increases with the atomic mass (with an important dependence on nuclear structure [38]), one expects an enhanced number of decay transitions mainly for mid and heavy nuclides. Such decays are subject to uncertainties, probabilities, and half-life definitions of decay patterns, which are not obvious.
The decay process and its uncertainties become more cumbersome as far as decay heat is concerned as very often the daughter product is also radioactive and can generate even more heat by further shorter decay processes. Ultimately, as will be shown in this section one has to deal with some unique decay pairs, or even to some extent decay chains, each of which, with its branching ratios and own heat production over different time scales.
As mentioned in the introduction, the integral amount of heat is well known to be around 7% of the operational power and a detailed analysis is not relevant. For long storage periods, the contribution of specific nuclides becomes considerably important. Considering again the quantum mechanics nature of the decay phenomenon, one has to separate the radioactive nuclides into different groups according to their decay types. Such an analysis includes the half-life time and decay mode. Further, one can analyze the mobility of such radioactive elements within and out of the repository. In the following subsections, the relevant elements are divided into actinides, fission products, and activation products. In addition, the specific pairs of radioactive materials with enhanced importance at different periods after shutdown are presented. The last part of this section demonstrates a quantitative analysis of those nuclides, which dominate the decay heat during the first 100 years, the realistic foreseen time of the temporary storage. The simulation is based upon a decay process of a PWR fuel assembly. For completeness, the decay heat at 300 years cooling time shows that the actinides are practically dominating more than 95% of the decay heat from that time slot, and the importance of other nuclides, in particular 137Cs/137mBa and 90Sr/90Y, fade away. Table 4 presents a list of the main energy fractions for each production mode during irradiation in atypical LWR.
It is relatively clear that the available energy from β decays and isomeric transitions represents about 7 to 8% of the total energy (approximately corresponding to the calculated decay heat from the Borst-Wheeler equation at the time of the reactor shutdown, see Eq. (6) in Sect. 6).
4.1. Overview
Several publications prior to the year 2000s and the older regulatory guides considered decay heat as a single integral quantity, see, for instance, references [40, 41]. More recently, as detailed in Section 6.4.1, the implementation of the summation method in computer codes for decay heat predictions provides a means to further isolate the nuclides responsible for most of the SNF decay heat power as a function of cooling time. Additionally, current decay heat standards treat the decay heat as a sum of individual components based on the physics of the decay process and nuclide generation under neutron irradiation (see details in Sect. 6.3).
Several studies have determined the most important medium-to-long-term decay heat contributors for spent LWR fuel and were used as a source in the following, see for instance reference [42]. This reference ranks individual nuclides by their contribution to the decay heat power. It also addresses the need for accurate source term predictions in commercial LWRs with higher levels of fuel enrichment and burnup. Figure 6 summarizes the findings from reference [42] for 5 years following reactor shutdown.
 |
Fig. 6. Contributions to the UO2 SNF decay heat for 5 years of cooling time. Numbers 3, 4, and 5 correspond to the initial 235U enrichment. |
As indicated in the figure, the decay heat power fractions of 90Sr and 90Y are added up as the two nuclides quickly reach a secular equilibrium. The same holds for 137Cs and 137mBa and 144Ce and 144Pr. The fractions of the total decay heat power produced by individual nuclides are displayed as a function of burnup and initial enrichment. Results are equivalent for both BWR and PWR and suggest a marginal dependence of the nuclide importance to decay heat on the LWR reactor type for cooling times longer than 1 year.
In the following paragraphs, the key nuclides contributing to the total decay heat of spent LWR uranium-fuel are discussed. Their production routes in a typical LWR are highlighted based on summation calculations using the simplified PWR model, as proposed in reference [43].
 |
Fig. 7. Actinide production scheme in irradiated reactor fuel. |
4.2. Delayed fission
A part of the decay heat comes from delayed fission events, induced by delayed neutrons. As delayed neutron precursors have relatively short half-lives, the delayed fission contribution is limited to the first 100 seconds after shutdown (in the case of a heavy water reactor, the photo-neutron source due to deuterium is large enough to affect the neutron population immediately after shutdown). The importance of delayed fission for decay heat after shutdown is presented in references [44, 45]. In reference [39], it was also shown that taking into account the delayed fission in reactivity-initiated accident (RIA) simulations significantly changes the calculated decay heat for a short time (a few seconds).
4.3. Actinides
During the irradiation of uranium fuel, transuranic nuclides build up mostly as a combination of multiple neutron capture reactions (n,γ) in the initial uranium and radioactive decay. Other threshold reactions such as (n,2n) or (n,p) occur at a much lower rate, making these production routes often negligible. In low-enriched uranium fuel, most of the neutron captures occur in 238U, producing fissile nuclide 239Pu from the rapid decay of 239U and 239Np. Many of the actinides created as a result of nuclear transmutation have much shorter half-lives than those of the uranium isotopes present in fresh fuel and can significantly contribute to the decay heat of spent LWR fuel. An overview of the transmutation mechanisms for the actinides buildup in irradiated nuclear fuel is shown in Figure 7. Only a few actinides are responsible for decay heat in UO2 fuel at any cooling time in comparison with a large amount of significantly contributing fission products.
Within the first few years following reactor shutdown fission products are the primary source of decay heat and the radioactive decay of actinides only generates a small fraction of it. In the first few hours/days of cooling this contribution comes mainly from the radioactive decay of the 239U and 239Np produced from the transmutation3 of 238U [47, 48]. As for other short-lived nuclides, their concentration and their role in decay heat is a function of problem-specific parameters such as the reactor-specific power. The 239U/239Np contribution dies out within a few days, after which alpha-emitter 242Cm, with a half-life of 142 days, contributes up to 90% of the actinide decay heat power up to 1 year. All other actinides with a non-negligible concentration at shutdown decay with longer half-lives and their contribution is only relevant for the long-term decay heat. In general in MOX fuel the actinide contribution exceeds the fission product decay heat power already after a few years of cooling. More than 99.5% of the total actinide decay heat in spent LWR fuel from 30 days up to more than 200 years from discharge is produced by seven actinides: 241Am, 242Cm, 244Cm, 238Pu, 239Pu, 240Pu and 241Pu [28].
239U/239Np
Days after discharge the actinide decay contribution comes primarily from the decay of short-lived nuclides 239U and 239Np, which have radioactive half-lives of 23.46 min and 2.356 days, respectively. 239U is produced from neutron capture in 238U and quickly beta decays into 239Np emitting beta and gamma radiation. The daughter nuclide 239Np further beta decays into 239Pu also releasing beta-electrons and gamma-rays. This decay sequence is reported in equation (2) and not only it represent the only significant production route of 239U and 239Np during irradiation, but also of the fissile nuclide 239Pu.
The 239U and 239Pu decay heat power was derived analytically in the decay heat standards [24, 26, 49], which cover explicitly their contribution to the decay heat of LWRs. A value for the 239U and 239Np short-term decay heat of spent LWR fuel strongly depends on the reactor operation condition. However, publications from the early 2000s and earlier show that it can represent up to more than 90% of the actinide decay heat power fraction (equivalent to about 20% of the total decay heat power) after the first day of cooling and it goes down to about 70% within 5 to 10 days [44, 47, 48].
239Pu/240Pu
239Pu is continuously created from the irradiation of 238U following the production route already presented in equation (2). Further irradiation of the nuclear fuel gives rise to plutonium isotopes 240Pu, 241Pu, and 242Pu as a result of neutron captures starting with 239Pu.
During nuclear fuel irradiation in a LWR this is essentially the only plutonium production route. 239Pu build-up gradually saturates with burnup as its fission rate increases. On the other hand, the production of the heavier plutonium isotopes accelerates at higher burnup values: an effect that is visible in Figure 8 for 242Pu because of its lower disappearance rate.
 |
Fig. 8. Build-up of the Pu isotopes in a LWR as a function of the assembly burnup. |
For 240Pu and 241Pu, which have respectively large capture and fission cross sections in a thermal LWR, the production and disappearance rates already balance out for burnup values of the order of a few tens of GWd/tHM or lower, depending on the fuel’s initial enrichment.
239Pu and 240Pu are both long-lived alpha-particle emitters with half-lives, of 24 110 and 6560 years, respectively. They release alpha particles with average energies of 5.156 MeV and 5.238 MeV. Because of the magnitude of these half-lives the decay of 239Pu and 240Pu is irrelevant during the fuel irradiation but becomes important to the SNF decay heat power already after 100 years of cooling with a contribution of a few percent and up to 20% after one thousand years. These numbers do not significantly vary with burnup and initial enrichment.
241Am
241Am naturally decays into long-lived 237Np with a half-life of 432.8 years. For one disintegration of 241Am an alpha particle is emitted with an average energy of about 5.48 MeV. Independently on whether the fuel is irradiated in a reactor or left to decay, the only significant production route of 241Am is from the radioactive beta decay of 241Pu (half-life of 14.33 years).
About 70 years after shutdown 241Am becomes the largest source of decay heat power in spent LWR fuel and it remains as such for a few thousand years. After one hundred years it generates almost half of the total decay heat power [42, 43], and about 70% of the actinide decay heat power fraction [44]. Its relative importance to decay heat is significantly affected by the SNF burnup. At high burnup and depending on the fuel’s initial enrichment the 241Am buildup during irradiation slows down as the 241Pu loss via neutron-induced fission increases. The 241Am relative contribution to the decay heat power in SNF with 70 GWd/tHM burnup and 5% initial enrichment drops to about 30% at 100 years of cooling time [42].
242Cm
The only significant production process of 242Cm in an LWR is from the neutron irradiation of 241Am. Neutron capture reactions in 241Am create 242Am, in its ground state with a probability higher than 90%. 242Am either beta decays into 242Cm or produces 242Pu from electron capture with a ratio of 83/17% and a half-life of 16.01 hours. The amount of 242Am in its first metastable state (i.e. 242mAm at 48.6 keV) formed during irradiation decays by internal conversion to its ground state with a probability of 99.5% and a longer half-life of 141 years. Despite being the only production process of 242Cm after shutdown, the decay chain of 242mAm is negligible to decay heat. 242Cm decays with a half-life of 162.9 days and emits alpha particles with a peak energy of 6.11 MeV (74% emission probability) which constitutes the majority of the recoverable decay energy. Already a few years after discharge essentially all of the 242Cm would be converted into 238Pu.
As for the other curium isotopes, 242Cm in nuclear fuel is generated from multiple neutron captures and, as such, its production accelerates at higher burnup levels. The 242Cm decay heat power fraction in spent LWR fuel is the highest after several hundred days of decay and it constitutes 80–90% of the actinides share [47]. This contribution remains below 5% of the total decay heat power [43, 50] as fission products are still the largest decay heat source within this time scale. For irradiated MOX fuel, 242Cm can contribute to more than 15% of the total decay heat at 1 year of cooling. For both fuel types, the relative importance of 242Cm for decay heat drops already a couple of years after discharge.
238Pu
238Pu naturally decays with a relatively long half-life of 87.7 years, principally by emitting alpha radiation and by a marginal fraction undergoing spontaneous fission. The emitted alpha particles have an average energy of 5.58 MeV per disintegration making 238Pu a considerable heat source with a specific power of about 0.55 W/g [51]. More than 90% of the 238Pu content in spent LWR fuel is produced via the neutron activation of 237Np shown in equation (3).
In turn, 237Np builds up either from a series of neutron capture reactions in 235U or as a result of the (n,2n) reaction in 238U. The fraction of decay heat power produced by 238Pu strongly increases with burnup. This effect is enhanced at longer cooling times to the detriment of 241Am, which ultimately saturates. The 238Pu contribution after 5 years of cooling varies from a few percent at low burnup up to more than 8% at high burnup. After 100 years it produces from 20% to 30% of the total decay heat power for a burnup range between 50 and70 GWd/tHM.
244Cm
At burnup higher than 30–40 GWd/tHM (or lower burnup for initial enrichments below 5%) 244Cm becomes the most present curium isotope in irradiated nuclear fuel. In SNF, 244Cm is practically entirely generated from neutron captures at 243Am, followed by the disintegration of the resulting 244Am in equation (4). Both isomers of 244Am beta decay into 244Cm with similar half-lives (i.e. 10.1 hours the ground state and 26 min the metastable state).
Basically, all the 243Am in irradiated fuel is created from the sequence of neutron captures in the plutonium isotopes reported in equation (5).
Other production routes including 242Am electron capture decay, neutron captures in americium or lighter curium isotopes are negligible. 244Cm decays with a half-life of 18.1 years emitting alpha particles with an average energy of 5.9 MeV.
4.4. Fission products
Radioactive fission products are mainly neutron-rich nuclides that carry most of the energy generated by the fission reaction in the form of kinetic energy. The majority of these fission products decay to more stable states via a combination of isomeric transitions and beta radioactive decays within seconds from their creation and up to a few hundred years. The gamma and beta-radiation released in the decay process is much smaller than that of a fission reaction, but it represents the largest share of decay heat load in uranium fuel up to nearly 100 years of cooling time. For typical LWRs the fission products generate up to 80% of the integrated decay energy between 1 and 10 years, that is when the decay heat power release is still large and a limiting factor for the licensing of storage installations [52].
For low-enriched uranium fuels in LWRs, more than 99% of the fission products contributing to the SNF decay heat are generated from neutron-induced fissions of four major fissioning nuclides: 235U, 239Pu, 238U, and 241Pu [28]. For each of these four nuclides, Figure 9 and Table 3 show how their fission rate fraction evolves as a function of burnup.
Up to more than 90% of fission events at the beginning of irradiation happens in the driver fissile nuclide 235U [53]. As 235U is consumed with burnup, more and more fissions occur in the 239Pu (and in a later stage in 241Pu) produced by neutron capture in 238U. For a lower initial enrichment, the fraction of fissions in plutonium becomes dominant at lower burnups. About 10% or fewer fission events occur in 238U because of its large abundance of uranium fuel, a figure that remains essentially constant with burnup.
Fission products contribute to the spent fuel thermal output to an extent that depends on their half-life and density in the fuel. Their decay heat power rapidly degrades because of the radioactive decay of the more significant energy emitters. Several decay steps along a decay chain are generally involved before reaching a stable nuclide. For cooling times longer than 30 days (and up to a few tens of years) about 95% of the total decay heat power is produced by 10 to 15 fission products, i.e. 89Sr, 91Y, 95Zr, 95Nb, 103Ru, 106Rh, 140Ba, 140La, 141Ce, 144Ce, 144Pr [54, 55]. By the end of the decay chains, longer-lived radioactive nuclides are typically formed such as 90Sr and 137Cs.
At cooling times between 1 and 70 years following shutdown, the fission products responsible for most of the decay heat power are only a handful. The dominant contributors are mostly parent-daughter pairs in secular equilibrium including 137Cs/137mBa, 90Sr/90Y, 106Rh/106Ru, and 144Ce/144Pr [56]. Since their precursors have fully decayed out along their decay chains, the content of these fission products in SNF can be qualitatively assessed from the analysis of their cumulative fission yields.
A significant decay heat power contribution also comes from nuclides created by neutron capture reactions in fission products during the irradiation of the fuel, such as 154Eu and 134Cs. The latter is identified by the decay heat standards as the dominant decay heat-generating nuclide resulting from neutron capture by fission products [24, 26, 57].
For cooling times between 1 and 5 years, the largest share of decay heat is produced by the decay chains of the relatively short-lived fission products 144Ce and 106Ru, and by the decay of activation product 134Cs generated by neutron irradiation of the stable fission product 133Cs. 10 to 30 years after shutdown the decay chains of 137Cs and 90Sr alone generate more than half of the decay heat rate of spent LWR fuel. 137Cs and 90Sr have similar half-lives and contribute in almost equal parts to the decay heat power for several decades until the role of the actinides becomes dominant. The 137Cs and 90Sr relative contribution increases marginally for less irradiated fuel because of the lower 134Cs buildup. For irradiated MOX fuel, the importance of these two nuclides drops by a factor of three because of the coincident contribution of actinides such as 238Pu and 244Cm.
106Ru/106Rh
106Ru is a short-lived fission product that emits beta radiation with a half-life of about one year. Practically the whole 106Ru content in spent LWR fuel is produced from fission reactions with cumulative product yields of 0.41% and 4.34% [58], respectively for thermal neutron-induced fissions in 235U and 239Pu (see Fig. 10).
 |
Fig. 10. Build up of the 106Rh nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
The heat generation from 106Ru is for a large majority produced by the radioactive decay of its daughter 106Rh. 106Ru disintegrates to the ground state of 106Rh emitting low-energy beta particles, and without releasing gamma radiation [59]. Its disintegration via neutron-induced reactions is negligible. The 106Rh half-life of only 30.1 seconds, much shorter than the half-life of 106Ru, implies a secular equilibrium between the two radionuclides. 106Rh decays by beta decay into 106Pd. About 10% of the decays goes to excited states that further decay releasing gamma rays. The recoverable energy released with the radioactive decay of 106Rh is 1.41 MeV and 0.21 MeV, respectively for light particles and electromagnetic radiation. The radioactive chain 106Ru/106Rh is ranked second amongst the decay heat power contributors for UO2 fuel at one year of cooling. The fraction of the total decay heat power after 5 years of cooling slightly increases with lower burnup and initial enrichment.
144Ce/144Pr
The 144Ce/144Pr decay chain produces the largest contribution to the decay heat power of spent LWR fuel 1 year after shutdown, with a growing relative importance for fuel with lower burnup. With cumulative yields of 5.48% and 3.76%, respectively for 235U and 239Pu thermal neutron-induced fissions, 144Ce is generated mostly as a fission product, see Figure 11.
 |
Fig. 11. Build up of the 144Ce nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
Only a relatively small fraction results from the activation of fission product 143Ce. 144Ce decays by beta decay into the ground state of 144Pr with a branching ratio of 98.85%, while the remaining 1.15% goes into the 144mPm (half-life of 7.2 minutes) at 59 keV above the ground state. In turn, 144Pr beta decays into long-lived 144Nd (half-life of 2.29 × 1015 years). Since the half-life of the daughter nuclide 144Pr is much shorter than the one of its parent 144Ce, i.e. respectively 17.29 min and 284.89 days, the two nuclides attain a secular equilibrium within about two hours [60]. The radioactive decay of both nuclides involves gamma-ray transitions of low intensity, and while 144Ce emits low energy beta electrons, the largest decay heat recoverable energy is associated with the high energy beta electrons of 144Pr, i.e. average recoverable energy of light particles of 1.026 MeV.
134Cs
Since 134Cs comes after the stable nuclide 134Xe in the A = 134 decay chain, its generation as a fission product from the A = 134 chain is limited to the direct contribution from fission, i.e. its cumulative fission yield equals its independent fission yield. In practice, because of the small value of this fission yield, the only significant 134Cs production path in a nuclear reactor is from neutron capture in the stable fission product 133Cs. Being at the end of the A = 133 mass chain, which only includes short-lived nuclides, the 133Cs cumulative fission product yield is relatively well known, especially for a thermal neutron-induced fission of 235U, i.e. 6.653%. Its cumulative yield for a 239Pu thermal neutron-induced fission is 6.844%, thus making the 133Cs production relatively invariant to the type of the fissioning system. 133Cs is an effective neutron absorber with a sufficiently large capture cross section for the formation of the 134Cs in its ground state and, with a probability lower than 1%, of its first metastable state at 138.7 keV [61]. 134Cs is constantly removed via radioactive decay and, during irradiation, additionally by neutron capture (see Fig. 12).
 |
Fig. 12. Build up of the 134Cs nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
134Cs mainly beta decays with a relatively short half-life of 2.064 years into excited states of 134Ba. Electron capture transition is also possible with very low probability, but it is irrelevant for practical purposes. The recoverable energy per disintegration consists of 163.5 keV and 1.555 MeV, respectively for light particles and electromagnetic radiation, with signature energies of 1365.2 keV (emission probability 3.02%) and 604.7 keV (emission probability 97.6%).
The 134Cs relative contribution to the decay heat rate of spent LWR fuel is the highest after about 3 years of cooling. After 5 years it ranks third, behind the decay chains of 90Sr/90Y and 137Cs/137mBa. Its production scheme makes its dependence on burnup close to quadratic (Fig. 12). As a consequence, its relative importance increases for higher burnup. In irradiated MOX fuel, the 134Cs fractional contribution is about two-fold lower compared to UO2 fuel.
137Cs/137mBa
137Cs has a low neutron capture cross-section (0.27 b at thermal energy), a relatively long half-life of about 30 years and large cumulative fission product yields that are only marginally dependent on the fissioning nuclide and neutron energy (i.e. 6.09% and 6.58% respectively for 235U and 239Pu thermal neutron-induced fission, see Fig. 13). Production from neutron capture by fission products in the A = 136 mass chains is excluded because of the low neutron absorption cross sections.
 |
Fig. 13. Build up of the 137Cs nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
These characteristics, together with the possibility of its clear identification via non-destructive gamma-ray measurements, make 137Cs universally used for fuel burnup measurements [62], as its concentration shows a near-linear dependence on burnup [53]. The only decay mode of 137Cs is via beta transition, with average recoverable energy for light particles of 179.89 keV, and the release of low-energy gammas-rays. The decay process yields stable nuclide 137Ba in its ground state with a probability of 5.64% and short-lived 137mBa with a probability of 94.36%. With a half-life of 2.552 min, 137mBa transitions into its ground state emitting a signature 661.7 keV gamma-ray with an emission probability of 85.1%, whose magnitude surpasses any generated bremsstrahlung [63]. Due to its short half-life, 137mBa cannot be treated separately and always in equilibrium with 137Cs.
Already after 5 years of cooling the 137Cs decay chain contributes to at least 20% of the total decay heat power in irradiated spent LWR fuel. This figure is only weakly affected by the initial enrichment and slightly decreases for higher burnup because of the growing importance of 134Cs. The 137Cs decay chain remains central for the characterization of SNF decay heat rate up to 100 years of cooling. In MOX fuel its relative importance diminishes to a maximum of 10% because of the larger actinides build-up and because of the contribution of the 238Pu, already present in the fresh fuel, to the decay heat power.
90Sr/90Y
The only significant production path of 90Sr in nuclear reactors is via neutron-induced fission reactions. The 90Sr production strongly depends on the fissioning system, with a larger cumulative product yield for a 235U thermal neutron-induced fission (5.68%) than for a 239Pu thermal neutron-induced fission (2.08%), see Figure 14.
 |
Fig. 14. Build up of the 90Sr nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
Because of its negligible absorption cross-section, 90Sr builds up almost linearly for small burnup, that is when the number of fissions in 239Pu is significantly smaller than the number of fissions in 235U.
With a half-life of 28.8 years, 90Sr undergoes beta decay without the emission of gamma rays. Its daughter product (90Y in its ground state) also beta decays into the stable nuclide 90Zr, with a half-life of 2.67 days and a negligible gamma-ray yield. The average recoverable energy of light particles from the decay chain includes both contributions of 90Sr and 90Y, respectively of 193.5 keV and 933.8 keV. As the half-life of 90Y is much shorter than that of 90Sr, both nuclides are normally in secular equilibrium. As for 137Cs/137mBa, also 90Sr/90Y contributes to slightly higher fractions to the total decay heat for less irradiated fuel. In irradiated MOX fuel, the fraction of decay heat coming from the 90Sr decay chain is much less significant because of the lower 239Pu fission product yield.
154Eu
154Eu has a negligible direct fission product yield as its decay chain is blocked by the stable nuclide 154Sm. Then, its production is almost exclusively driven by the neutron absorption in 153Eu (312.6 b at thermal energy), whose production from thermal neutron-induced fission in 239Pu is larger than in 235U: cumulative fission yields of 0.38% and 0.15%, respectively (see Fig. 15). 154Eu has a large neutron-absorption cross-section of 1353.1 b at thermal energies and it is continuously depleted during irradiation. Because of the 154Eu relatively long half-life of 8.6 years, radioactive decay plays a minor role in the nuclide loss during the reactor operation, with the primary destruction channel being neutron-induced capture reactions. 154Eu disintegrates almost entirely (> 99.9%) via beta decay to excited states of the stable nuclide 154Gd. Of the emitted beta decay energy, on average 270.242 keV and 1.244 MeV are recoverable respectively from light particles and electromagnetic radiation. Given its relatively long half-life and strong gamma-ray signature, 154Eu is frequently used as a burnup monitor for long cooling times [64, 65].
 |
Fig. 15. Build up of the 154Eu nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
4.5. Activation products
Light elements are also present together with the nuclear fuel inside the core, in the form of rod cladding (usually made of zirconium alloys), or grids (also called spacers) to hold together rods (usually also made of zirconium alloys, or stainless steel). These elements were selected for their neutronic characteristics (low absorption) and also because they are corrosion-resistant materials. But still, neutrons can interact with these structural materials, via neutron capture, and create radionuclides which will eventually decay and produce an amount of decay heat.
Additionally, in the case of some older generation 3 loop PWR, part of the reactor internals are made of hard metal alloys, which contain a substantial amount of cobalt. Specific fuel assembly spacers can also be found with cobalt impurities, as high as 10 000 ppm. The nuclide 60Co is therefore of time, both for immediate dose rate, but also as an activation product.
4.6. Example of nuclide contributions for typical PWR burnup simulation
To illustrate the contributions described in the previous paragraphs, a number of examples are provided in the following. The relevant nuclides are shown from 6 months to several tens of years of cooling. The main characteristic calculations were performed for a typical theoretical PWR operating up to 55 MWd/kgHM (with an average enrichment of 4% and a total mass of 20 tons). The calculations employed the standard option of the NUCLEONICA Program [66] for the spent fuel inventory, using the JEFF-3.1 nuclear data library. The list of nuclides in Table 5 presents more than 98% of the nuclides contributing to the decay heat at 6 months cooling time and therefore are the main nuclides to be looked at for cooling times in this range.
Heat generated by the most dominant nuclides (98.2% of the generated heat), 6 months after reactor shut down for a representative 55 MWd/kgHM burnup.
Four nuclides have a very short half-life and their precursors should be examined too. 144Pr with a half-life time of 17.28 min is a decay product of 144Ce, which appears also on the list and has thereafter a particular importance, contributing about 25% to the total generated heat. This pair is mentioned in Section 4.4.
Another important nuclide is rhodium 106Rh with a half-life time of 30 seconds. Its precursor is ruthenium 106Ru with a half-life time of 1.02 years. At such time after shutdown, the decay of 106Ru is of crucial importance and, through the daughter decay of 106Rh, accounts for about 22% of the whole generated heat. This pair is mentioned as well in Section 4.4.
The third nuclide is the isomer 137mBa. This is a daughter product of 137Cs. Its importance is not as large as the contributions of the above-mentioned two nuclides, as it represents only about 4% of the heat at this period of time. Nevertheless, the 137Cs have a half-life time of about 30 years and, through 137mBa, the main contributor to heat production at later time periods as will be discussed below. Further details of the pair 137Cs/137mBa are also found in Section 4.4.
The same arguments mentioned above for 137Cs are also valid for 90Y and its precursor 90Sr. Again, as for 137Cs, the 90Sr has a half-life time of about 28 years, which increases its importance at longer decay times (see also 90Sr/90Y in Sect. 4.4).
The calculations for the same operational conditions as in Table 5 were repeated for a cooling time of 2 years. In this case, Table 6 shows the growing importance of 137Cs and 90Sr while the nuclides with half-lives of up to a few months like 89Sr, 103Ru etc. die away. Table 6 presents the spent fuel vector after 2 years for elements contributing about 98.2% of the heat produced, where indeed the contributions of 89Sr and 103Ru are marginally small and the contributions from these nuclides are neglected.
Past 5 years of decay time, 137Cs and 90Sr become the most dominating nuclides as far as the generated heat is concerned.
In a benchmark calculation led by SKB Sweden [15], the nuclides that contribute to the decay heat were isolated and analyzed by several codes. The importance of the main nuclides can be seen for five cases, from 4 years, up to 22 years of cooling time, in Table 7. The pairs 137Cs/137mBa and 90Sr/90Y generate about 40% up to 61% of the decay heat at the time range of 4.5 to 21.5 y respectively. Again, as shown by the former calculation, the contribution of 134Cs (half-life time 2 y) vanishes in this period as well as the contribution of 106Ru.
After 20 years, the importance of the decay heat has a direct impact on the geological disposal beyond the interim storage. As far as the nuclides are concerned, the minor actinides become more dominant. Nevertheless, the pairs 137Cs/137mBa and 90Sr/90Y generate about 50% of the heat. However, the overall heat is about two orders of magnitude smaller in comparison with the decay heat after 2 years. With half-lives of about 30 years, the influence of 137Cs and 90Sr decreases strongly towards 300 years, while as mentioned above, the actinides start to dominate the heat generation of the spent fuel.
At periods of about 40 to 50 years, the quantity of SNF that can be disposed of together depends on its heat load and on the geological conditions. Salt rocks can conduct heat better than clay. However, for the safety of a waste disposal, the mobility of potential radioactive materials within the hosting rock becomes one of the crucial criteria for the loading scheme within the disposal casks, with the aim of controlled heat removal and radioactive dose in the storage gallery. Those issues are beyond the scope of this chapter.
However, the change of the governing nuclides as far as their heat decay is concerned is emphasized in Tables 8 to 10, for 40, 100 and finally 300 years of decay time. The daughter products 90Y and 137mBa from 90Sr and 137Cs respectively die away after 300 years equal to about 10 half-life time periods of those pairs.
5. Measurements
Measured data of decay heat are of prime interest for the understanding of the energy released by SNF and for the validation of decay heat codes, standard methods, and nuclear data. The quality of such data ultimately determines the confidence users have in their simulation tools. Substantial efforts to measure total energy releases from irradiated samples, and also separated contributions from isomeric transitions and β decays, were made more than 50 years ago: pulse and long irradiations on small enriched actinides samples, using thermal or fast neutrons, from 0.1 seconds to tens of thousands of minutes of cooling time, and more recently on full scale irradiated spent fuel assemblies.
Despite these extensive campaigns, limited experimental data are available for the validation of simulation codes and nuclear data libraries. Some of the first measurements suffer from large uncertainties (concerning today’s capabilities), inconsistencies, and more recently, integral decay heat measurements on full SNF present high correlations between themselves due to the limited number of facilities and studied cases. It was also noticed that the existing set of measured SNF decay heat values does not cover the characteristics of today’s fuel: high enrichment, high burnup, and interest in short and long coolingtimes.
In the following, a list of the most representative experiments is presented, with some details. Readers will notice that pulse irradiation of small samples were not performed for decades and that integral SNF decay heat measurements nowadays rely on a unique facility (Clab, Sweden), notwithstanding the worldwide importance of SNF storage.
5.1. Calorimetric measurements
First calorimetric measurements were performed in the 50s using galvanometers and ion chambers for irradiated uranium rods, or the decay energy absorbed by the full-scale reactor, see references [67, 68] for details. These experiments were able to cover a cooling range from 0.1 to 108 seconds. These types of measurements are not described in the following but are the predecessor of more modern calorimetric measurements for SNF assemblies. A general overview of more recent integral measurements of decay heat for entire SNF assemblies, using calorimeters is presented in Table 11. Some details are provided below.
Summary of existing integral decay heat measurements using calorimetric methods.
Summary of existing decay heat measurements using calorimetric methods on LWR SNF assemblies.
5.1.1. General information
United States
Comprehensive summary of measurements performed in the U.S. has been compiled by Roddy and Mailen in 1987, representing the HEDL and GE-Morris Operation facilities [69]. A schematic overview of both calorimeters is presented in Figure 16 [70, 71].
The General Electric spent fuel storage facility in Morris, Illinois (GE-Morris facility) used a pool calorimeter and in total 111 different decay heat measurements were performed between 1980 and 1985 on 14 PWR fuel assemblies (reactors Point Beach 2 and San Onofre 1) and 61 BWR assemblies (reactors Cooper, Dresden and Monticello) [52, 72, 73]. Seven decay heat measurements were also reported on five PWR assemblies from the Turkey Point 3 reactor. These measurements were performed between 1980 and 1983 using a boil-off calorimeter operated at the Engine Maintenance Assembly and Disassembly facility (EMAD) on the Nevada Test site of the Handford Engineering Development Laboratory (HEDL facility) [70, 74]. No measurements were reported in the USA after the decay heat measurements of spent fuel coming from the Monticello reactor and the calorimeters have been decommissioned since.
A summary of the US decay heat measurements associated with fuel design description, and reactor operating data needed to perform decay heat calculations benchmarks are given in the validation report of the SCALE code for LWR Spent Nuclear Fuel by Gauld et al. in reference [52]. This validation study is based on the data compiled by the Energy Information Administration of the U.S. Department in Nuclear Fuel Data Survey Form RW-859 of 2004. Complementary information is also available in the Schmittroth and Roddy reports published by HEDL and ORNL laboratories [69, 70, 74].
The systematic bias for the GE-Morris measurements is about ±4% in the 200 W range and ±2% around 700 W. For the HEDL decay heat measurements, ±10% in the 100 W range was reported and drops to ±5% for values greater than 1000 W, as mentioned in reference [52].
Finally, it is worth noticing the use of an underwater calorimeter at the Bettis Atomic Power Laboratory [75] for the measurements on small samples (a few grams for 233, 235U and 239Pu).
Sweden
In 2004, SKB initiated a program at the Clab facility (Central Interim Storage Facility for Spent Nuclear Fuel) to provide decay heat data in support of the characterization of spent fuel applicable to the design and operation of wet and dry facilities and also for the future national fuel repository at Forsmark [76]. The Clab calorimeter used a design similar to the GE-Morris one. Up to 2006, 145 calorimeter measurements on full-length assemblies were reported for 34 PWR assemblies (reactors Ringhals 2 and Ringhals 3) and 50 BWR assemblies (reactors Barsebäck 1, Barsebäck 2, Forsmark 1, Forsmark 2, Forsmark 3, Oskarshamn 2, Oskarshamn 3, Ringhals 1); experimental values, assembly data and operation history were reported in reference [76], as well as in SCALE analysis [76–78].
In 2014, additional measurements performed between 2006 and 2010 were reported by Ilas et al. [79]. They mainly concern the same SNF as in previous references but with more recent measurements. These cases (not yet publicly available at the time of writing) would be interesting as they represent multi-measurements over a few years.
In 2017, five new measurements for 5 different PWR assemblies were proposed by SKB for the so-called “blind decay heat calculation benchmark”, and results were published in reference [15, 80]. These PWR assemblies corresponded to higher enrichments and burnup values compared to the previous Clab reported data in reference [76], therefore nicely complementing the existing set. More recently, reference [12] is referring to new Clab measurements performed from 2015 to the present. It is also indicated that the description of such 60 new measurements will be published soon.
Japan
These Japanese-reported experiments are the only ones currently performed on MOX assemblies [81–84]. Such assemblies were designed to be used in the experimental sodium-cooled fast reactor JOYO and therefore do not correspond to designs of LWR MOX fuel. Enrichments in 235U and Pu were reported sensibly higher than for LWR for the measured assemblies (13 to almost 30%). These measurements are reported in Table 11 but cannot simply be used or compared to measurements for LWR assemblies.
France
In France, two different types of measurements were realized: one on the decay heat for the full core of the sodium-cooled fast reactors Phénix and Superphénix [85] and one on a single UO2 rod [86]. One can add measurements performed at the ZOE reactor on small samples (a few grams) with a dedicated calorimeter [87].
In the case of Phénix and Superphénix, experiments on decay heat measurements on French Sodium Fast Reactors (SFR) were performed between 1979 and 1996. However, due to the final shutdown of Phénix scheduled in 2010, it was decided to perform a new test as part of the Phénix end-of-life experiments: the PUIREX experiment [88]. A calorimetric method based on the thermal balance of the reactor circuits was used. No actual calorimeter such as in Clab or GE-Morris was needed. The decay heat of the full core was deduced for low power (about 10 MW) and predicted calculations were validated. This type of experiment, giving access to the decay heat of the entire reactor is only feasible in sodium-fast reactors thanks to the sodium inertia in the pool configuration of the reactor. As in the case of the JOYO measurements, such results are not of relevance to the present work but correspond to the only published decay heat data for afull core.
The second published measurement, part of the MERCI program, concerns the irradiation of a single UO2 rod, at the periphery of the experimental reactor OSIRIS [86]. Characteristics of the irradiation can be seen in Table 11. The decay heat was measured using the MOSAÏC calorimeter (by means of heat transfer to water). The main advantage of this case consists of its short cooling time and low burnup, helping to validate decay heat calculations linked to 235U fission products.
The experimental uncertainties for the measured decay heat are also relatively low: between 1 and 3%.
5.1.6. Details
MERCI-1 experiment (France)
A fresh PWR UO2 fuel rod sample (active length of 40 cm) with a 3.7 wt.% content in 235U and zircaloy-4 cladding, within a stainless steel containment, was irradiated during 55 equivalent full power days in the periphery of the OSIRIS reactor [86]. The layout of the MERCI device in the OSIRIS pool is reported in Figure 17.
The discharge burnup of the MERCI fuel rod was about 3.6 GWd/tHM. The fuel rod was transferred in 26 min from its irradiation location to a hot cell to be inserted into the MOSAÏC calorimeter. The released decay heat was measured from 27 min to 45 days after shutdown. Over this period the decay heat decreases from about 200 W to 4 W. Post-irradiation examinations were also performed at the CEA/LECI laboratory in order to measure the concentrations of the main actinides (uranium, plutonium) and burnup trackers (neodymium, cesium) in a sample located at the middle of the fuel rod. These post-irradiated examinations allowed an accurate evaluation of the fuel rod burnup and axial distribution. The fuel rod axial distribution was also measured by gamma-ray scanning inside the OSIRIS pool with a high-purity germanium detector system.
The OSIRIS reactor is an experimental reactor with a thermal power of 70 MW. It is a light water reactor, open-core pool type. The MERCI device was located in the periphery of the OSIRIS reactor core and was made up of two mechanical components: the fuel rod to be transferred and its support structure, equipped with core instrumentation, i.e. rhodium self-powered neutron detectors to measure the thermal neutron flux, cobalt detectors for safety purposes, one removable fission chamber, and activation dosimeters to measure the axial neutron fluence profile.
The MOSAÏC calorimeter was designed [89] and patented by the CEA [90]. The MOSAÏC calorimeter design is based upon the heat pipe principle where the cold element is the condenser and the warm element is a tungsten cylinder, which also reduces gamma-ray leakage thanks to its high density (about 18 g/cm3), see Figure 18. The tungsten absorbs about 96% of the total gamma-ray emission. The gamma-ray leakage was evaluated by calculation. The MOSAÏC calorimeter was designed with the particular goal to have a precision of 1% and to have minimal heat losses. The residual heat is deduced by a heat balance measurement on the secondary system using accurate instrumentation such as platinum resistance thermometers and Coriolis flowmeters.
Two analysis of the MERCI-1 experiment were performed, one with the 3D full pointwise Monte Carlo code TRIPOLI-4® [91] and one with the deterministic 2D lattice code APOLLO2 [92] coupled with the depletion code PEPIN2 [93], which performs the depletion calculation with very precise depletion chains describing the buildup and disappearance of more than 3800 nuclides and the exact depletion history of the MERCI-1 experiment.
The axial neutron flux calculated by TRIPOLI-4 is corrected in order to fit with the measured axial gamma-ray scanning. At the end of the depletion and cooling period, the nuclide concentrations are compared to the measured ones, and the neutron fluence is adjusted in order to minimize the discrepancies on the main actinides and burnup trackers.
In addition to this calculation, the gamma-ray leakage and the activation of the structural components are also evaluated by computation. The gamma-ray leakage has been evaluated with TRIPOLI-4 and PEPIN2 (JEFF-3.1.1 nuclear data library) by integrating the energy of the gamma-rays that escape the first enclosure of the MOSAÏC device. The calculated gamma-ray heat loss fraction (gamma-ray heat loss/total decay heat) is plotted in Figure 19. The gamma-ray leakage is comprised between 2% (around 42 days) and 4% (around 30 min). The gamma-ray leakage follows mainly the gamma heat loss of the 140La, which has high gamma-ray energy (1.6 MeV). The 140La is also the main contributor to the decay heat between 17 hours and the end of the measurement period. The energy produced by the activation of the cladding has also been evaluated with PEPIN2 calculations. It appeared that the contribution of the cladding to the total decay heat is comprised of between 0 and 2.25% at the maximum around 1.5 hours of cooling.
Between 27 min and 45 min a measurement bias was observed due to an unexpected thermal transient after the introduction of the MERCI fuel rod inside the calorimeter: the MERCI fuel rod stored heat during the transfer phase from the reactor pool to the hot cell. Thus, during the first 800 seconds, the measurement overestimates the effective residual heat produced by the MERCI fuel. This unforeseen energy storage amount cannot be calculated or estimated because of a lack of appropriate instrumentation.
The measurement uncertainty with the MOSAÏC calorimeter is between ±1% and ±2% depending on the cooling time. This uncertainty has been evaluated from the propagation through the MOSAÏC calorimeter numerical model of measurement errors (temperature, mass flow rate) and thermo-physical properties (density, specific heat, enthalpy, thermal conductivity). The uncertainty due to the neutron flux adjustment is ±0.7%. Bias due to the calculation scheme has been estimated to be under ±0.2%. This point has been checked by using two different methods for the neutron calculation (Monte Carlo and deterministic), in addition to several sensitivity studies on the calculation scheme choices.
The nuclear data uncertainties were recently reevaluated with both deterministic and stochastic methods that produced very similar results [94]. The nuclear data uncertainty on the decay heat of the MERCI fuel is about 4% at the beginning of the measurement period and rises up to 11% at the end of the measurement period. The main contributors to the variance of the decay heat are the independent fission yields of 235U in the thermal range (for this calculation, independent fission yields are not correlated, which maximizes the total uncertainty in this time period). All these uncertainties are independent of each other and result in a global uncertainty calculated by quadratic summation comprised between 5% and 12% at 2 standard deviations.
The calculation-over-experiment discrepancies (C/E − 1) are plotted in Figure 20. The gray area represents the total uncertainty at two standard deviations. A satisfactory agreement is observed between 5 and 42 days of cooling where the discrepancies are under ±1%. The maximum discrepancy is about 6% at 12.5 hours of cooling. Between 45 min and 36 hours, the discrepancies are included in the analysis uncertainty at 2 standard deviations. Between 36 hours and 42 days, the discrepancies are within the analysis uncertainty at 1 standard deviation.
 |
Fig. 20. Calculation over measurement discrepancies (red line) associated with the total uncertainty (measurement, modeling, and nuclear data) at two standard deviations [94]. |
MERCI-1 is the first experiment that enables the integral validation of decay heat issued from the disintegration of 235Uth fission products and the 239U/239Np decay. This program demonstrated the feasibility of such an experiment, at very short cooling times and with a very low experimental uncertainty. Nevertheless, additional experiments at higher burnup or with depleted UO2 fuel or MOX fuel are mandatory. Indeed, a recent work has been performed on the MERCI-1 experiment in order to quantify the similarity of this experiment to a UO2 fuel irradiated in a PWR regarding nuclear data [95]. The results show that the similarity of the MERCI-1 experiment with the UO2 fuel decreases drastically with the burnup of the UO2 fuel. Even at 10 GWd/tHM, the contributions of the 239Pu fission products cannot be neglected, which makes the MERCI-1 experiment not appropriate to validate codes for the decay heat of PWR UO2 fuels at burnup higher than 10 GWd/tHM.
Concerning additional decay heat measurements performed at the PHENIX reactor (France), called the PUIREX experiment, details can be found in Appendix A.
The Clab experiments (Sweden)
The intermediate fuel storage facility at Clab allows for performing calorimetric measurements of nuclear fuel assemblies for BWRs and PWRs [76]. As mentioned, the design of the Clab calorimeter is similar to that used at GE-Morris. A five-meter-long cylinder is placed inside a water pool and can contain the full length of a nuclear fuel assembly, thus allowing for a non-destructive measurement, see Figure 21. The calorimeter is hermetically sealed to prevent water in the pool from comeing into contact with the water inside the calorimeter during the measurement. A centrifugal pump circulates water in the calorimeter to maintain a homogeneous temperature in the measurement chamber. Sixteen temperature sensors are located in the water inside the calorimeter, on the internal and external surfaces of the calorimeter, and in the water outside the calorimeter to measure the increase in temperature. The calorimeter is calibrated with an electric heater with well-known power. Dose rate monitors are placed outside the calorimeter to measure the quantity and radial distribution of the gamma-ray radiation that escapes from the calorimeter. Corrections are applied for the fraction of the released gamma-ray heat absorbed outside of the calorimeter.
The decay heat of a nuclear fuel assembly is determined with the temperature increase method. The measured increase rate of the temperature is compared to the corresponding calibration measurements and the decay power is determined. The gamma-ray radiation field is also measured and the power escaped gamma-ray heat is determined. The total decay heat power is derived from the sum of the measured decay power and the measured power from the escaped gamma rays. This method has the advantage of being relatively independent of the gamma-ray heat leakage since leakage also occurs during calibration. On the other hand, compensating factors must be added to account for the fact that fuel assemblies have a different volume, mass, and material composition than the electric heater. The realistic measurement time necessary to carry out a calorimetric measurement for one fuel assembly is one day.
After the measurement campaign involving the “blind decay heat benchmark” in 2017, a new analysis of the experiments, including calibration, escaped gamma-rays (simulations) and detectors was undertaken until 2023, in collaboration with EPRI. New measured decay heat values are planned to be publicly distributed, with low uncertainties (in the vicinity of a few percent).
The calorimeter project in Switzerland
The development, installation, and commissioning of a new full-scale calorimeter to measure the decay heat of spent fuel assemblies at Gösgen Nuclear Power Plant (KKG) is currently under consideration. This calorimeter would allow the measurement of UO2 PWR fuel with very high burnup (up to ∼70 GWd/t) and high enrichment (up to 5%), as well as MOX fuel. The concept of the calorimeter is aimed at achieving a high level of measurement precision.
The mechanical structure of the Gösgen calorimeter is shown in Figure 22 and consists of a shaft for holding the fuel assembly, with vacuum insulation to minimize heat transfer between the calorimeter and the vessel basin and a lid that is closed to perform the measurement. The lid is made of polyethylene and is pressed against a seal by a slight under pressure, preventing uncontrolled mass transfer with the basin contents. This implies that if there is no active circulation, the lid is released, and the fuel is cooled by natural convection (internal KKG safety condition). The calorimeter has a modular design and can be operated in three different modes (three main feed/intake points, as illustrated in Fig. 22). One of the three possible functionalities is depicted in Figure 22, where the mass flow is depicted by arrows (mass flow from the lower inlet line to the upper section line). A lead, steel-coated, shielding is also designed to absorb almost 100% of the gamma-ray losses (to increase the measurement accuracy). The decay heat is determined by temperature differences between outlet and inlet lines and the water mass flow, in a reached steady-state system.
 |
Fig. 22. Layout of KKG calorimeter (left) and cross-section of the shielding design (right). |
The measuring station will be set up at the edge of the container basin of the external wet storage facility. The calorimeter will be mounted on a fuel rack normally used for fuel inspection, under ∼7 m water. More details will be published in the coming years if the project successfully continues.
5.2. Gamma-ray and beta-particle measurements
Apart from the calorimetric measurements presented in the previous section, for “large” samples, a number of other experiments, using specific calorimeters were also performed on small samples (as previously mentioned at Bettis [75], ZOE [87], but also in the UK [96]). Dedicated γ-ray and β-electron emission detectors were also used. Some details are provided in the following.
5.2.1. Historical measurements
In the 1960s and 1970s, a number of experiments were performed to measure the decay energy release rates from fission events, from short irradiation of small samples. These data are extremely useful for code validation (see for instance Ref. [97]), as presented later in Section 6.4.4. Additionally, a number of experiments, with some code inputs were compiled by the IAEA under the CoNDERC project. A summary of some measurements is presented in Table 13 and in mentioned references.
Summary of existing differential decay heat measurements for neutron-induced fission on specific systems. Measurements are given in MeV/s/fission.
Note that additional measurements were performed on other actinides, such as 232Th, 233, 238U and 237Np. Depending on the type of experiment, the total energy release rates, with or without the β-electron and γ-ray components are measured and presented. Selected measurements are presented in this section and a more detailed description of a number of experiments can be found in reference [118].
Liquid scintillator
A number of measurements for the total energy release were performed with a large absorption scintillator, absorbing virtually all beta-electrons and gamma-rays [75, 103, 105, 110, 119]. Typically, such calorimeters were very large (a few thousand liters), and made of different modules of plastic cylinders coupled to photomultiplier tubes. A rabbit system was used to bring irradiated samples to this instrument in a matter of seconds. Samples (for instance enriched uranium deposited on aluminum backing) were irradiated with a moderated neutron source (for instance 252Cf surrounded by water) for various periods, each of them followed by a calorimetric measurement.
Separated β-electron and γ-ray measurements
In order to obtain the contributions from the β-electron and γ-ray emissions, some measurements were performed with scintillators such as NaI for γ-ray detection, and with Si(Li) detectors for β-electrons. Small samples were irradiated with thermal or fast neutrons, and transported with a pneumatic system in front of the dedicated detectors. Measurements were separately performed for β-electron and for γ-ray detection, see, for instance, references [108, 120, 121]. A different approach is followed in reference [96], based on Calvet microcalorimeter measurements: it corresponds to a multicel calorimeter using a uranium shell surrounding the sample and absorbing a large part of the emitted γ-rays.
Compilation and data selection
The previous experiments for the total or β-electron and γ-ray energy release rates are currently extensively used for code and nuclear data validation (mainly fission yields and decay data), as presented in Figures 28, 31 and 32. They are nevertheless not directly compared to calculations, but the comparisons are based on specific compilations, or evaluations, as from Tobias et al. [122], on selected and trusted sets of measurements from Dickens, Akiyama, and Schier (Lowell) [107, 123–127]. For more details on the validation of nuclear data with these data, see Sections 6.4.3 and 6.4.4.
5.2.2. Detection of gamma-rays from short-lived fission products
The description provided in the following concerns the detection of gamma rays from short-lived fission products at KUCA and KURNS-LINAC in Japan. More details on these studies can be found in reference [128].
Introduction
For new types of reactor cores, the residual heat removal system must be designed carefully to prevent elevation of the temperature of fuel cladding. For the design, the residual heat during the initial quarter of an hour after the shutdown of the core is naturally of high relevance. The residual heat is mainly determined by the decays of fission products (FPs) with a half-life of less than an hour. The yields of FPs and their decay data (yields and decay types) have comprehensively been evaluated up to now. However, isotopic validations of those yields and data are not trivial.
Recently, radiations were measured at Kyoto University Critical Assembly facility (KUCA) and at Kyoto University LINAC pulsed neutron source facility for specific purposes. As byproducts, gamma rays from short-lived FPs were measured. In the following, the measurements were reported.
Critical experiments
Some of neutron-induced reactions are followed by emissions of gamma rays of intrinsic spectra to the reactions. Thus, gamma-ray spectrometry would give information on the ratio of rates of some reactions occurring in neutron multiplication systems including a critical core. Then a mocked-up was built for the critical core in a light water tank at KUCA and the gamma rays outside the tank were measured as shown in Figure 23 left.
 |
Fig. 23. Left: Side view of the critical core and HPGe detector. Yellow lines are of aluminum alloy. Right: Measured γ-ray spectrum for critical core. |
428 sheets of plate-type fuel of uranium (U) and aluminum (Al) alloy were loaded vertically to the core bottom base made of stainless steel. The 235U enrichment of the fuel is 93 wt.%. An HPGe with 30% relative efficiency was used for the gamma-ray detection. The photo-electric (PE) peaks of gamma-rays from capture reactions of 1H, 27Al, 53Cr, 56Fe, and 58Ni and 235U were detected as well as the single and the double escape peaks (DE, SE) of those. Gamma-ray peaks from de-excitation of 16mO are also found. The pulse height spectrum from 2900 to 4900 keV is shown in Figure 23 right. The base continuum spectrum is due to the prompt gamma-rays from fission of 235U. Above the continuum part, small peaks stick out. Except for PE, DE, and SE components originated in the 27Al(n,γ) reaction, more than ten peaks are found. The spectrum was compared to the evaluation in JENDL/FPY+FPD-2011, followed by the identification of peaks of which the count rate is dominated by the decay of 88Br, 89Kr, 90, 90m, 91, 92Rb, 95, 97, 98Y, and 136Te.
The peak-to-base ratio is small due to the intense prompt fission gamma-rays and the statistical errors of those peaks range from 2 to 20% for four hours of measurement with a power of 4.6 mW. In this measurement, the FP gamma-ray was measured during neutron irradiation so that FP of half-lives shorter than 4 seconds (97Y) was detected.
Out-of-phase measurement for small sample
Gamma-ray spectra were measured for a small U sample of the natural 235U enrichment irradiated by a pulsed neutron source at KU-LINAC. The neutron was generated by photo-interactions with a tungsten target and the fast neutron was slowed down in light water moderator. The pulse frequency was 50 Hz and the time from pulse generation to a gamma-ray detection was measured to determine incident neutron energy for the gamma-ray emission reaction. The flight path length was approximately 11 m. The time spectrum for the gamma-ray detection is shown in Figure 24 left.
 |
Fig. 24. Left: Time of flight spectrum for estimation of energy of incident neutron. Right: γ-ray spectrum at time background. Nuclides in labels denote β-decay parents of delayed γ-rays. |
The original purpose of this experiment was to detect 238U(n,γ) gamma-rays for the thermal and the resonance energy neutrons and so peak structures are found in Figure 24 left. However, after decay out of the thermal neutrons, gamma-ray events were still detected, corresponding to out-of-phase events. In such a case, there is no neutron, indicating that the fission and capture reactions would not be induced. Such events are therefore due to some radioactive decay. Currently, it is expected that those decay were from FPs originating in 235U in the sample although the initial enrichment was 0.72 wt.%. The gamma-ray spectra for the out-of-phase events are shown in Figure 24 right, where peak components can be observed. By the attenuation of the prompt fission component, the peak-to-base ratio of them is better than those in Figure 23 right. Comparing the measured data to the JENDL/FPY+FPD-2011, peaks dominated by 89Kr, 90, 91Rb, 95, 97, 98Y were identified. Gamma-rays were also measured during neutron irradiation, the gamma rays from 97Y were also measured by this method.
Future plan
The new techniques are potentially useful for the validation of fission product yields and their associated decay data. In these critical experiments, the estimation of the detection efficiency of the FP gamma-rays needs to be determined. A possible method is to rely on gamma-ray transport calculation with the PHITS or the MCNP-6 codes assuming or calculating spatial fission distribution. Currently, the normalization of the calculated efficiency is under study. Another issue is related to the background from 27Al(n,γ) gamma-rays. Accordingly, critical experiments with fuels with different ratios of Al/U in another facility might be beneficial.
In the out-of-phase measurement, an open question is related to the amount of 238U fission events since the neutron spectrum above 30 eV was not measured at the facility. To remedy this, it is planned to perform Cd filtered and non-filtered measurements were scheduled with enriched U samples. Those decay data have recently been re-evaluated in the JENDL-5 nuclear data library, and comparisons between the measured and calculated gamma-ray spectra will be highly beneficial.
6. Calculation methods
As the decay heat of SNF is seldom measured, the importance of its estimation through calculations is crucial. There are globally three different possibilities:
-
based on a single formula, with various degrees of complexity,
-
based on more advanced methods presented in various national and international standards,
-
and based on the summation method.
Historically, the first developments have led to the derivation of formulas, which depended on a limited number of parameters, and are therefore labeled in the following as “simple formula”. Such an approach followed the calculation capabilities at that time, as well as the past needs. Valuable information was obtained (such as the well-accepted value of “7%” residual heat after a reactor shutdown, or general aspects of exponential decay of the decay heat), and allowed some finer developments integrated into the decay heat standard methods. Such methods were developed over decades (from the 1970s to today) and will be presented in the following. Both simple formulas and standard approaches generally have a range of applicability and cannot be applied to any cooling time and fuel type.
More recently, the ability to perform accurate decay heat calculations based on a summation approach (coupled with a precise neutron transport and depletion calculations) has sensibly improved, mostly due to the availability of evaluated nuclear data as well as more affordable computer power. Such developments will also be presented in this section.
6.1. Simple formula
Under specific needs, the decay heat can sufficiently be well approximated by the known Borst Wheeler formalism [2] (see Appendix B for details):
where the Borst Wheeler function definition contains P(t, T), the power emitted at time t after the shutdown of a reactor that operated for time T, as well as P0, the reactor power.
The origin of this expression comes from the idea of dealing with the heat contribution of isomeric transitions and β decays. Borst and Wheeler (as well as Glasstone and Sasonke [129]) use the classical approach based on Way and Wigner [38]. The difference is the weight given to the β(t) and the γ(t) decay. Nevertheless, by combining both contributions of the γ(t) and the β(t) decay, one can get very similar results.
It is of course “tempting” to adjust this formula to measured values. The 200 MeV/fission used in the above equation can be adjusted to the more correct energy release per fission 202 MeV/fission (for 235U thermal neutron induced fission in a typical LWR), etc., the 2.7 MeV/s can also be changed to other numbers beyond the 2.8 MeV/s as proposed by Glasstone [129]. Further ideas appear in more complicated expressions.
In reference [129], Glasstone introduces a more general method where two parameters, a (multiplier) and b (power parameter), can be changed. One can explain this procedure by the fact that the α decay is not included in the original considerations and as compensation, a better fitting to measured data occurs by tuning the existing parameters (see Fig. 25 for a simple comparison with different approaches).
 |
Fig. 25. Decay heat ratio P/P0 as presented in equations (8)–(B.12), compared to the early ANS-5.1/N18.6 standard from 1971. The irradiation time T is considered infinite (1013 seconds). |
Todreas and Kazimi [130] proposed a more detailed approach for the exact evaluation of the decay heat, at the very beginning of the shutdown phase.
They additionally define the heat generated by delayed neutrons in a very short time (0–80 seconds) after shutdown. In parallel, a more fundamental approach for the shutdown is given by Duderstadt & Hamilton [131], based on the point kinetic equation and derive the decay heat power by integrating the time over the changing reactivity during the fall of the shutdown control rods.
Except for the very sophisticated approach mentioned above, the approach of Way & Wigner [38] that was adopted by Borst Wheeler, Glasstone, and others to provide a very good solution for times from 0 to about 106 seconds. Beyond that period, the impact of the α decay is noticeably growing, and as it is not included, the results are expected to be worse. In addition, the fact that most of the reactors are idle for maintenance for about 30 days between successive cycles is also a source of inaccuracy, as it is not taken into account in the formula shown above.
In view of the mentioned limitations, the Borst Wheeler formula was tested against several measurements obtained from reference [15]. The decay time was between 108 and 109 seconds. The maintenance time between the cycles was ignored which indeed showed more conservative results. Overall, the decay heat ratio (decay heat to nominal power heat of the reactor) was over-estimated by a maximum of 60%. Using the solution of Glasstone [129, 132] (which is supposed to be applicable up to 8 × 108 seconds) underestimates the results by up to 60%, which is for safety reasons not conservative, and hence not recommended. Full adaption to the measurable results can also be mathematically achieved by further adjustments of the time parameters, albeit without physical foundation.
Consequently, the safety considerations for waste disposal afford much higher accuracy, which can be only achieved by “tedious” burnup calculations. Nevertheless, some of these early studies of the pioneers of the nuclear technology can support and provide useful guidance for the range of decay heat one is concerned with, even at relevant long-time disposal.
6.2. Delayed fission
After a reactor shutdown, fission events can continue to happen, not initiated by prompt neutrons (emitted about 10−14 seconds after a fission event), but due to neutrons emitted by fission products after β decays (delayed neutrons), by (α,n) or (γ,n) reactions, or simply from spontaneous fission. Delayed neutrons can be emitted from milliseconds up to a few hundred seconds (for the longest-lived precursor 87Br), as long as precursors are produced. These sources of delayed neutrons can also induce fission events, called delayed fission, therefore contributing to decay heat. In practice, such contribution from β decays is rapidly vanishing compared to other sources, as indicated in Figure 26.
 |
Fig. 26. Example of decay heat (with delayed fission); Top: for a UO2 fuel, enriched at 3.5%, with a burnup value of 33 MWd/kgU. Bottom: Same for a MOX fuel enriched at 5.30% (Pu content) with a burnup value of 60 MWd/kgHM. Extracted from a French REP900 [133]. |
In the present context, delayed fission is therefore different from the definition given in references [134, 135], where it corresponds to a nuclear decay process that couples 13 decay and fission, mainly corresponding to an exotic decay mode of excited heavy actinides.
In reference [133], two examples for different fuel assemblies (one UO2 and one MOX) are presented, with the calculated contributions from delayed fission to the total decay heat (see Fig. 26). As observed, although delayed fission is the main contributor shortly after shutdown, its contribution becomes negligible after about 100 seconds. It can be considered that delayed fission is of no importance for SNF storage, but on the contrary, it can be of high importance in the case or slow or fast transients [39].
6.3. Standards
Standard methods for decay heat calculation were originally developed to provide a means to determine decay heat values with an accuracy comparable to that of summation methods but with less computational effort and without the need for excessive nuclear data libraries.
Due to the limited number of input quantities the standard methods are often easier to use than summation methods, especially for users who are not experts in the field of decay heat. Some methods also provide guidance for a specific application. With regards to licensing procedures, depending on the regulatory framework in a given country, the usage of decay heat standards may also reduce the effort in a license application or in some cases even be mandatory.
Nowadays, calculations based on best-estimate codes, using the summation method, are more easily accessible than historically, rendering the use of standards less unavoidable. As presented in the following and in the example in Section 6.3.7, standard values can sensibly depart from values based on the summation method. It is also interesting to realize that standard methods often require as inputs quantities such as “power per irradiation steps”, or fission fractions per irradiation steps (fraction of 235U, 238U, 239Pu and 241Pu to the total fission rates, for each irradiation steps), which can only be accurately obtained from best-estimate codes (e.g. SCALE/POLARIS, CASMO5, Serpent).
6.3.1. Overview
A variety of standards (or standard methods) was developed over time, with numerous releases and updates. The latest releases at the time of the present work are as follows: the JAERI-M 91-034 from 1991 [57], the ANSI/ANS-5.1 from 2014 [136], the DIN 25462-1 and -2 from 2014 [22, 25], the U.S. NRC RG 3.54, Rev. 2, from 2018 [28], and finally the ISO 10645, from 2022 [27].
Despite some differences in the methods and the level of self-sufficiency, the latest revisions of the standards adopted a common approach. The total decay heat power is computed as a sum of contributing sources instead of the empirical formulation based on tabulated correction factors used in the earlier revisions. The identified major decay heat sources considered in the latest releases are:
-
Fission products,
-
actinides, and
-
neutron capture (n,γ) on fission products.
The standards usually neglect spacial effects of energy disposition (from γ radiation) and the decay heat contribution from delayed neutrons and activated structural components. Each of these standards presents limits on the applicability, defined based on
-
Reactor type (PWR or BWR),
-
fuel type (UO2 or MOX),
-
decay time after irradiation,
-
fuel properties, burnup, and enrichment.
The mentioned standards apply almost identical methods for the evaluation of the decay heat due to the decay of fission products, except those generated by neutron capture on fission products.
Similar semi-empirical methods are used, except in DIN 25463 1/2 (2014), for the decay heat due to neutron capture in fission products and fully empirical for the decay heat from the actinides. Indeed, the DIN standard is using explicit analytical methods for the evaluation of the decay heat from the decay of fission products generated by neutron capture in fission products as well as from the decay of the actinides.
In terms of self-sufficiency, the standards can be divided into entirely self-sufficient, such as the DIN 25463 1/2 (2014) and U.S. NRC RG 3.54 Rev.2 (2018), and standards requiring special input data, dependent on operating conditions, reactor type or fuel type, prepared by the user: ANSI/ANS-5.1 (2014) and ISO 10645 (2022). For example, the ANSI/ANS-5.1 (2014) requires knowledge (and justification) of the fission fractions for the major four fissionable nuclides 235U, 238U, 239Pu and 241Pu, at each irradiation interval, the production rate of 239U from capture on 238U at end of irradiation, as well as the number of fissions per initial fissile atom (FIFA). Similarly, the ISO 10645 (2022) requires the fission fractions however provides a formula for the production rate of 239U from capture on 238U. Tables 14 and 15 summarize the main standard characteristics and applicability area; details will be provided in the following sections, but readers are encouraged to read the original standard publications for a full understanding.
Main standard characteristics concerning their latest releases.
Main standard limits and applicability concerning their latest releases.
In the case of MOX fuel for the DIN standard, the amount of Pu fissile content is defined as (239Pu+241Pu) divided by (U+Pu+Am). Therefore the amount of 241Am is indirectly included in the Pu fissile content. Increasing the amount of 241Am may lead to leaving the area of applicability by lowering the Pu fissile content. 241Am is not added to 239Pu and 241Pu in the numerator since it is not fissile in the sense that the capture cross section is usually larger than the fission cross section in the thermal spectrum (this is also reflected in cross-section data given in the standard).
6.3.2. DIN 25463-1 and -2 standards, 2014
The standard provides the basis for calculating the decay heat power of uranium oxide nuclear fuel in pressurized water reactors by taking into account the contribution of fission products from nuclear fission, the contribution of actinides, and the contribution of decay heat power resulting from neutron capture in fission products. By its definition, the standard is entirely self-sufficient hence requires no special, reactor, or fuel type, or operating conditions-dependent data to be supplied by the user.
History
The history of the German standard for the calculation of decay heat power, DIN-25463, begins in 1982:
-
Fission products: from summation of 23 exponential terms for 235U, 238U and 239Pu from ANSI/ANS-5.1-1979,
-
Actinides: 239U and 239Np,
-
Correction term to account for actinides other than 239U and 239Np,
-
Explicit formula with approximated neutron flux for 134Cs production,
-
G-factor for neutron capture in fission products other than 133Cs.
DIN 25463 1990:
-
241Pu is added as fissionable nuclide
-
Fission products: 24 exponential terms for 235U, 238U, 239Pu and 241Pu,
-
Minor corrections.
DIN 25463-2 2008:
-
newly developed standard for PWR MOX fuel.
DIN 25463-1/2 2014:
-
Decay time < 2 × 109 sec. (≃63 years),
-
MOX fuel
-
Fission products: 24 exponential terms for 235U, 238U, 239Pu and 241Pu,
-
Actinides: explicit depletion chains,
-
Neutron capture in fission products: explicit activation chains,
-
Extended range of applicability for enrichment and burnup.
Besides the standards for light water reactor fuel, there is also a DIN standard for nuclear fuels of high-temperature reactors with spherical fuel elements [137]. This standard will not be further discussed here since it is outside the scope of the present paper and has been withdrawn lately.
Applicability and limitations
The standards are applicable UO2 and MOX fuel irradiated in pressure water reactors (PWR), under the following conditions:
-
Not applicable to fuel depleted in BWRs,
-
Decay time shorter than 2 × 109 s (≃ 63 years),
-
Uranium enrichment: 3 − 5 wt.%,
-
Fissile plutonium in HM: 1.8 − 7.5 wt.%,
-
Fissile plutonium in total plutonium: 50 − 80 %,
-
Fuel to moderator ratio: 1.8 − 2.4,
-
Maximum burnup for UO2: 80 MWd/kgHM, and for MOX: 60 MWd/kgHM,
-
Maximum 235U in MOX fuel: 0.72 wt.%,
-
Decay heat power from activation products in structural materials and fission power from delayed neutron-induced fission are not included.
Methodology
The total decay heat rate/power Pz after a decay time t which follows a power period T, is a sum of contributions from fission products, actinides, and decay heat generated by nuclides formed by neutron capture in fission products:
with
-
PS: the decay heat rate from fission products from fission of 235U, 238U, 239Pu, and 241Pu.
-
PR: the decay heat rate from actinides and neutron capture in fission products.
The decay heat from fission products PS is computed by approximating a pulse power function by a sum of 24 exponential terms multiplied by the reaction rates Ri of the four main fissile nuclides and integrated over the power intervals k. The pulse power function, fi(t), represents the decay heat power per fission, following an instantaneous pulse of a significant number of fission events. The data represent fi(t) and its assigned 1σ uncertainty for thermal fission of 235U, 239Pu, and 241Pu, and for fast fission of 238U. The decay heat power is obtained in (MeV/fission⋅s) and converted to W⋅s by ϵ = 1.6022 × 10−13 W⋅s/MeV:
with
-
ϵ: conversion coefficient from MeV/s to W,
-
λi, j, αi, j: the coefficients in the 24-term exponential fit for the fission products decay heat power,
-
Ri, j: the fission fractions of nuclide i (235U, 238U, 239Pu and 241Pu) in step k,
-
−T,t the time on power and cooling time, for the step k.
The fission fractions, Ri, j, are determined by burnup calculations, depleting the actinides.
The decay heat due to radioactive decay of actinides and decay of nuclides generated by neutron capture in fission products is treated explicitly by solving the burnup equations for the nuclide atom densities Nn via prescribed depletion and decay paths, with cross sections, decay constants λn and recoverable energies Qn provided by the DIN documentation:
with Nn(t, T) the solution of system of burnup differential equations for 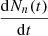 .
.
The actinides included explicitly are: 234 − 239U, 237 − 239Np, 238 − 243Pu, 241, 242, 243, 244Am, 242, 244Cm. The nuclides included in the decay heat due to capture in fission products are: 110mAg, 134Cs, 136Cs, 140La, 148, 148mPm and 154, 156Eu.
The DIN provides a set of effective data: cross sections, neutron capture and fission along with the basic decay data such as atomic masses, decay constants, fission yields, and recoverable energies, in the form of interpolation tables. The data interpolation for UO2 fuel is defined by enrichment and moderator-to-fuel ratio. An additional parameter, the fissile share in plutonium, is used in the interpolations for MOX fuel. The standard provides a formulation for the neutron flux which is determined for each burnup step by an iterative procedure. The uncertainty in the computed decay heat power is determined from the uncertainties of the sources contributing to decay heat power: fission products without neutron capture in fission products, actinides, neutron capture in fission products, and the uncertainty in the operating power. The uncertainty of the computed total decay heat is calculated by:
with
-
n: the statistical uncertainty in term of [sigma],
-
ΔPS: the uncertainty decay heat power from fission products,
-
ΔPR: the uncertainty in decay heat power from actinides and neutron capture in fission products,
-
 : the relative uncertainty in the nominal thermal power,
: the relative uncertainty in the nominal thermal power, -
Qi, ΔQi: nuclide energy per fission and uncertainty,
-
λi, j, βi, j: coefficients in the 24-term exponential fit for FP uncertainties,
-
Ri, k: fission rate fraction of isotope (235U, 238U, 239Pu and 241Pu) in step k,
-
t, T: time on power and cooling time (same for step k: tk, Tk).
For the uncertainty decay heat power from fission products (ΔPS), the expression is given by
and
For the uncertainty due to the actinides and neutron capture in fission products, ΔPR can be expressed as follows, following the same definitions as previously mentioned:
6.3.3. US NRC RG 3.54, revision 2, 2018
It is stated that the regulatory guide (RG) provides methods that are acceptable to the U.S. Nuclear Regulatory Commission (NRC) staff for calculating spent nuclear fuel heat generation rates for use as design input for an independent spent fuel storage installation (ISFSI). By its definition, the regulatory guide is entirely self-sufficient hence requires no special, reactor, fuel type, or operating conditions (apart from the power history) dependent data to be supplied by the user.
History
Revision 1, 1999
-
Empirical formula with table interpolated factors with dependency on burnup and enrichment,
-
Maximum burnups of 45 MWd/kgU (BWR), and 50 MWd/kgU (PWR).
Revision 2, 2018
-
Extended ranges for burnup and enrichment,
-
The empirical procedure is replaced by sum of contributing sources,
-
Fission products: 9 exponential terms for 235U, 238U, 239Pu and 241Pu from ANSI/ANS-5.1-2014,
-
Actinides: semi-empirical procedure for 7 actinides,
-
Neutron capture: explicit for 134Cs production; tabulated correction factor for the rest,
-
Activation products in structural materials: tabulated corrections factor.
Applicability and limitations
The methodology used in the guide is appropriate for computing the heat generation rates of fuel assemblies from LWRs as a function of burnup, specific power, decay time, and enrichment up to 5 weight-percent (wt.%) 235U in uranium.
-
Applicable for UO2 depleted in either PWR or BWR,
-
Not applicable for MOX fuel,
-
Decay times from 1 year to 110 years,
-
Initial 235U enrichment : 2 to 5 wt.%,
-
PWR, burnup applicability range: 10 to 65 MWd/kgU,
-
BWR, burnup applicability range: 10 to 60 MWd/kgU,
-
Average power: from 12 to 50 kW/kgU.
Methodology
The total decay heat, PT(t, T), after a decay time t which follows a power period T, is computed as a sum of the following separate sources and corrected by a safety factor FS:
with
-
PF: decay heat power from fission products,
-
PC: decay heat power from neutron capture in 133Cs to product 134Cs,
-
PE: decay heat power from neutron capture in other fission products,
-
PA: decay heat power from actinides,
-
PS: decay heat power from activated structural materials, and
-
FS: a safety factor.
The decay heat from fission products, PF(t, T), is computed by approximating a pulse power function by a sum of 9 exponential terms multiplied by the reaction rates Ri of the four main fissile nuclides and integrated over the power intervals k. The pulse power function, fi(t), represents decay heat power per fission following an instantaneous pulse of a significant number of fission events. The decay heat power is obtained in (MeV/fission⋅s) and converted to W⋅s by ϵ = 1.6022 × 10−13 W⋅s/MeV:
The method and the data are those developed for ANSI/ANS-5.1-2014. The nine group coefficients λi, j and αi, j, provided by the standard, are applicable for SDC times longer than 1 year. The PC(t, T), the decay heat due to radioactive decay of 134Cs generated by neutron capture in 133Cs is given by the following equation:
with
-
Y: effective cumulative 133Cs yield per fission (in percent),
-
λ4: decay time constant 134Cs (s−1),
-
σ3: spectrum averaged (n,γ) cross section in 133Cs (barn),
-
σ4: spectrum averaged absorption cross section in 134Cs (barn),
-
E: recoverable energy per decay for 134Cs (MeV),
-
ϕ: total neutron flux (n/cm2.s),
-
S: specific operating power (MeV),
-
Qi: specific energy per fission for the four fissionable nuclides (MeV),
and
The quantity Si, k is the specific thermal operating power generated by the fission of nuclide i for irradiation interval k. The relative power fractions for each of the four fissionable nuclides Si/S is tabulated as a function of initial enrichment and burnup, and reactor types PWR and BWR. The average specific power during step k is determined from the burnup Bk and irradiation time Tk.
The PE(t, T), the decay heat power from neutron capture in fission products except for 133Cs is determined from the decay heat of the fission products PF and reactor independent factors tabulated as a function of decay time H(t):
The decay heat from actinides is calculated as the sum of contributions from seven nuclides: 241Am, 238 − 241Pu, 242Cm, and 244Cm, tabulated via time and power factors. The time-dependent part is computed as:
with 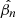 are coefficients calculated as:
are coefficients calculated as:
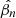 are the tabulated constants depending on reactor, burnup and enrichment, λ1 and λ2 the decay time constant for 241Am and 241Pu, and E1, E2 the recoverable energy for 241Am and 241Pu. The decay heat power from the decay of actinides is obtained by applying a correction factor to the average power:
are the tabulated constants depending on reactor, burnup and enrichment, λ1 and λ2 the decay time constant for 241Am and 241Pu, and E1, E2 the recoverable energy for 241Am and 241Pu. The decay heat power from the decay of actinides is obtained by applying a correction factor to the average power:
with Savg the average power is computed as:
The PS(t, T) component, the decay heat power from activation in structural materials is designed to account mainly for the production of 60Co. The decay heat power is determined from the decay heat of the fission products PF and factors tabulated as a function of decay time A(t):
As for the safety factor, FS(t), the definition given by the guide is: “An additional safety factor is applied to allow for uncertainties in the predicted values of the decay heat power obtained using the methods and data in this guide”. The safety factor is tabulated as a functions of decay time.
The guide does not provide methods or data related to the uncertainties. It is quoted: “The uncertainty is found to be relatively small and largely independent of burnup over the range of the data. The methods are found to yield conservative estimates of decay heat on average. The safety factor includes additional statistical allowance to ensure that the values obtained using the guide are conservative with respect to 95 percent of the measurement data at a 95-percent confidence level. The safety factor also addresses potential non conservatism resulting from the procedures of the guide and other approximations”.
6.3.4. JAEA standard, JAERI-M 91-034, 1991
The decay heat and related quantities reported in this work correspond to recommendations from the “Committee of Standardization of Decay Heat Power in Nuclear Reactors”, organized by the “Atomic Energy Society of Japan” [49, 138]. It applies to LWR (also to Fast Breeder Reactors), and corresponds to decay heat from fission products, including the decay of 239U and 239Np, but excluding the decay heat from actinides, from the activation products in structural materials, as well as from delayed neutron-induced fission.
Fission products from five origins are considered in this work: thermal neutron-induced fission of 235U, 239, 241Pu and fast neutron-induced fission of 238U and 240Pu.
6.3.5. ANS standards
The standards provided by the American Nuclear Society (ANS) have evolved and refined over the past decades. We present here a very simplified history, to understand the developments of such ANS standards. Because the ANS standards are being developed using rules allowing each standard to be approved by the American National Standards Institute (ANSI), the standards are often referred to as ANSI/ANS, followed by a specific reference number and year.
Prior to the standard released in 1979, the first draft standard (ANS-5.1/N18.6) was based on predictions of fission products’ decay heat by Shure [139]. Such “evaluation” effort was based on computational and experimental works [140, 141]. The decay heat refers to reactors initially loaded with uranium fuels and operated at constant power (P0), as expressed by the previous functions presented in previous paragraphs; Figure 25 presents the calculated decay heat as ratios of P/P0, for the 1973 ANS-5.1 standard, as well as the calculated curves from the various equations. A detailed history of the development of the 1973 standard (as well as the following one of 1979) can be found in reference [142].
Such draft standard was suffering from two main inaccuracies: (1) that the decay heat contributions from different fission products were equal, and (2) that the neutron capture effects were negligible. The correction of such deficiencies has led to a new standard, issued in 1979 (ANSI/ANS-5.1-1979), and reaffirmed4 in 1985. Details of the new standard can be found in reference [143]. It mainly focuses on cooling time less than 104 seconds, although it covers cooling periods up to 109 seconds, based on an upper bound for the capture correction. It also explicitly accounts for differences in the fission products from 235U, 238U, and 239Pu; neutron capture in fission products is taken into account using a correction factor, as it will be later done in many decay heat standards. Additionally, this 1979 standard considered changes in fissile content during the fuel life (this was a new development compared to the previous standard and to the previous functions presented in the above paragraphs). In the ANSI/ANS-5.1-1979 standard, the decay heat from fission products is represented in two ways.
Differences in the ANS standard versions (1979, 1994, 2005, 2014, and 2019) consist in the number of considered fissioning systems (241Pu is taken into account from 1994), the considered measured and calculated decay heat values.
-
ANSI/ANS-5.1-1994
-
ANSI/ANS-5.1-2005
-
ANSI/ANS-5.1-2014 (reaffirmed in 2019)
History
This American National Standard provides values for the decay heat power from fission products and actinides following the shutdown of light water reactors operated with nuclear fuel consisting of uranium. ANSI/ANS-5.1 was first proposed in 1971, the revised proposal submitted in 1973, and officially released in 1979 notified as ANSI/ANS-5.1-1979.
-
Applicable to t < 109 seconds,
-
Fission products: summation of 23 exponential terms for 235U, 238U and 239Pu,
-
Actinides: 239U and 239Np, and
-
Neutron capture in fission products by a G-factor.
In the 1994 revision, the following changes were applied:
-
Applicable to t < 1010 s,
-
241Pu is added as fissionable nuclide,
-
Updated 238U data, and
-
Revised uncertainty data.
For the ANSI/ANS-5.1-2005, minor corrections and recommendations were implemented, whereas in the latest ANSI/ANS-5.1-2014 revision, correction terms to account for actinides other than 239U and 239Np were added, and the production of 134Cs was taken into account.
Applicability and limitations
The standard is applicable to LWRs containing 235U as the initial major fissile material and 238U as the fertile material. The decay heat contributions from 235U, 238U, 239Pu, and 241Pu are treated explicitly; other fissionable nuclides are accounted for by treating them as 235U:
-
Applicable for decay times shorter than 1010 seconds (about 316 years),
-
Inapplicable for MOX fuel, and
-
Decay heat power from activation products in structural materials and fission power from delayed neutron-induced fission is not included.
Methodology
The total decay heat power from the fission products and actinides is calculated as:
where the contributing decay sources are from
-
P′d(t,T): fission products from fissions of 235U, 238U, 239Pu, and 241Pu,
-
Pdc(t,T): neutron capture in fission products
-
G(t): correction factor,
-
PCs(t, T): decay heat from capture in 133Cs,
-
PdE(t, T): fission products other than 133Cs,
-
PdHE(t, T): for 239U and 239Np, and
-
PdA(t, T): for other actinides.
The decay heat from fission products, P′d(t, T), is computed by approximating a pulse power function by a sum of 23 exponential terms (j = 1, …, 23) multiplied by the fission fraction (Ri) of fissile nuclide (i = 1, 4) and integrated over interval (k = 1, N) at constant power.
with
-
ϵ: conversion factor from MeV/s to W,
-
λi, j (and αi, j): coefficients in the 23-term exponential fit, (i = 4, j = 23),
-
Ri, k: fission rate fraction of nuclide i (235U, 238U, 239Pu, 241Pu) in step k,
-
T, t: time on power and cooing time, step k.
The four sets of 23 coefficients αi, j and λi, j, are provided by the standard for the thermal fissions of 235U, 239Pu and 241Pu, and the fast fissions of 238U. The formulation is derived from the analytical solution of the integral for
The integral gives the decay heat power of fission products resulting in of the fission of fissionable nuclide (i), during irradiation interval at constant power (k). The function fi(t) representing the decay heat power per fission following an instantaneous pulse of a significant number of fission events is defined as:
The fission fractions Ri depends on the fuel type and the operating conditions and must be provided by the user.
The decay heat due to neutron capture in fission products, PdC(t, T), for shutdown times t ≤ 104 seconds is based on corrections to the decay heat of fission products G(t)-factor calculated as:
The irradiation time T is limited to 1.2614 × 108 seconds (about 4 years) and the Fissions per Initial Fissile Atom (FIFA) should be Ψ < 3. The FIFA and Ψ must be evaluated and supplied by the user. For shutdown times t > 104 seconds, the standard provides a tabulated correction factor H(t). In addition, the standard applies explicitly the contribution from 134Cs being produced by the neutron capture in 133Cs:
with parameters as defined earlier:
-
P′d(t, T): fission products from fissions of 235U, 238U, 239Pu and 241Pu,
-
PdCs(t, T): decay heat from capture in 133Cs is defined by
with
-
Y: effective cumulative 133Cs yield per fission (in percent),
-
λ4: decay constant of 134Cs (s−1),
-
σ3: spectrum averaged (n,γ) cross section in 133Cs (barns),
-
σ4: spectrum averaged absorption cross-section in 134Cs (barns),
-
E: average energy per decay for 134Cs (MeV),
-
ϕ: effective neutron flux (n/cm2.s):
-
Sk: specific power density (MW/tUinitial)
-
ϵeff: effective enrichment (wt % of initial 235U)
-
P/Q: effective fission rate defined as
-
Pi, j: specific operating power for nuclide i (MeV),
-
ϵeff: specific energy per fission (MeV).
The PdE(t, T), the decay heat power from neutron capture in fission products except for 133Cs is determined from the decay heat of the fission products P′d and reactor independent factors tabulated as a function of decay time H(t):
The contribution to decay heat power from actinides is computed by two separate sources. The decay heat power from the decay of 239U and 239Np, PdHE(t, T), and the decay heat power from actinides other than 239U and 239Np, PdA(t, T):
with
and
-
EU: average energy from decay of 239U (MeV),
-
ENp: average energy from decay of 239Np (MeV),
-
R: 239U production from capture in 238U at the end of irradiation (at/s),
-
λU: decay constant of 239U (s−1), and
-
λNp: decay constant of 239Np (s−1).
The production of 239U (R-factor) must be computed and provided by the user. The contribution to decay heat of all other actinides is accounted for by a tabulated correction factor, and with dependence on burnup and initial enrichment, applied to the uncorrected contribution for neutron capture decay heat of fission products by the following equation:
with A(t) a tabulated correction factor, B the burnup, ϵeff the effective 235U enrichment (wt.% of initial 235U), and
The total uncertainty is determined from the uncertainty in the fission product decay heat power without neutron capture in fission products and the uncertainty in the operating power. The other terms in the total decay heat, neutron capture in fission products and actinides, are defined to provide conservative overestimates of their contributions to the decay heat power, and the uncertainties in these terms are therefore not included in the total uncertainty:
with P, ΔP the reactor power and reactor power uncertainty. The decay heat uncertainty of fission products ΔP′d is defined by:
The four sets of 23 coefficients βi, j used in the calculations of the uncertainty are provided by the standard for the thermal fissions of 235U, 239Pu, and 241Pu, and the fast fissions of 238U.
6.3.6. ISO 10645 (2022)
The standard provides procedures for calculating the decay heat power of non-recycled nuclear fuel irradiated in light water reactors. The methods apply to light water reactors (pressurized water and boiling water reactors) loaded with a nuclear fuel mixture consisting of 235U and 238U. By its implementation, the methods applied in this standard are very similar to those in ANSI/ANS-5.1-2014.
History
The first released in 1992 is almost identical to DIN 25463 1990:
-
applicable to PWR and BWR,
-
for fission products: 24 exponential terms for 235U, 238U, 239Pu and 241Pu,
-
with explicit formula with approximated neutron flux for 134Cs production,
-
based on a G-factor for neutron capture in fission products other than 133Cs,
-
explicit description for both actinides 239U and 239Np,
-
correction factor to account for actinides other than 239U and 239Np,
-
initial 235U enrichment up to 4.1 wt.%,
-
and a burnup limit of 52 MWd/kqU.
The 2022 implementation has the following characteristics:
-
Fission products: 23 exponential terms for 235U, 238U, 239Pu and 241Pu from ANSI/ANS-5.1-2014,
-
initial 235U enrichment increased up to 5 wt.%,
-
Burnup range is extended to 62 MWd/kgU,
-
Decay time less than 109 seconds,
-
New procedure for neutron capture in 133Cs, and
-
Updated formulations and nuclear data.
Applicability and limitations
The following limitations and range of applications need to be considered:
-
The methods in the standard are applicable to UO2 depleted in either PWR or BWR.
-
The standard is not applicable to MOX.
-
The standard is applicable for cooling times from 0 to 109 seconds.
-
The standard yields conservative results for:
-
Initial enrichment a0, between 1.9 wt.% ≤ a0 ≤ 5 wt.%,
-
Burnup Bf ≤ 12.5 a0 MWd/kgU,
-
Power density S ≥ 5 a0 kW/kgU.
-
Decay heat power from delayed neutron-induced fission and activation of structural materials are not included. The user is advised to evaluate those and appropriately include them in any analysis of decay heat.
Methodology
The total decay heat PN after a decay time t which follows a power period T, is computed as a sum of the following separate sources:
where
-
PS: the decay heat power from fission products,
-
PB: the contribution of 239U and 239Np,
-
PA: the contribution of other nuclides,
-
PCs: the contribution of 134Cs, and
-
PE: the decay heat power from neutron capture in other fission products.
The decay heat from fission products is computed by approximating a pulse power function by a sum of 23 exponential terms multiplied by the reaction rates of the four main fissile nuclides and integrated over the power intervals (k). The power function, the innermost sum in the equation below, represents the decay heat power per fission following an instantaneous pulse of a significant number of fission events:
with the following factors:
-
λij, αij: the coefficients in the 23-term exponential fit for the fission products decay heat power,
-
Pij: the fission rate fraction of nuclide i (235U, 238U, 239Pu and 241Pu) in step k,
-
Qi: the specific energy per nuclide i (235U, 238U, 239Pu and 241Pu), and
-
t, T: the time on power and cooling time for step k.
The method and the data are those developed for ANSI/ANS-5.1-2014. The 239U and 239Np contributions to decay heat are treated separately from the rest of the actinides:
Measured and calculated decay heat value for the Ringhals-3 assembly 0E2.
The term Pk/Q is the total fission rate in time interval k, and the terms FU(tk, Tk) and FNp(tk, Tk) are computed by:
with
-
EU, λU: the mean decay energy and decay constant of 239U,
-
ENp, λNp: the mean decay energy and decay constant of 239Np, and
-
R the ratio of capture in 239U to total fission rate at the end of operating time.
An approximation for R is provided as a function of initial enrichment a0 and final burnup Bf:
For initial enrichments between 1.9 wt.% and 5 wt.%, the approximation yields conservative results. The decay heat from decay of actinides other than 239U and 239Np, is determined from the decay heat power from fission products multiplied by tabulated vs decay time factor A(t):
It stated that it will “yield conservatively high results”, provided the following conditions are fulfilled:
-
Initial enrichment, 1.9 wt.% ≤ a0 ≤ 5.0 wt.%,
-
Burnup ≤ 12.5× a0 MWd/kgU, and
-
Power density ≥ 5.0 × a0 kW/kgU.
The decay heat due to radioactive decay of 134Cs generated by neutron capture in 133Cs is given by the following equation:
with
and
-
y the mean cumulative 133Cs yield per fission,
-
λ4 the decay time constant for 134Cs (in sec−1),
-
σ3 the spectrum averaged (n,γ) cross section in 133Cs (in barn),
-
σ4 the spectrum averaged absorption cross section in 134Cs (in barn),
-
ECs the recoverable energy per decay for 134Cs (in MeV),
-
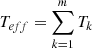 the effective irradiation time excluding outage periods,
the effective irradiation time excluding outage periods, -
Qi the specific energy per fission for the four fissionable nuclides (in MeV),
-
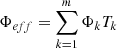 the effective neutron flux (given in n/cm2/s).
the effective neutron flux (given in n/cm2/s).
The value of Φk is given by Φk = Sk/aeff × 2.58 × 1013 with Sk the power density (in kW/kgU) and aeff = a0/2 + 1.0, being the effective enrichment (in wt.%).
The approximate neutron flux yields conservative PCs for typical LWR enrichments and burnups by up to 5%. For burnup values less than 25 MWd/kgU, the approximate solution overestimates PCs by up to 15%.
The PA, the decay heat power from neutron capture in fission products except for 133Cs is determined from the decay heat of the fission products Ps and reactor independent factors tabulated as a function of decay time H(t):
The uncertainty of calculated decay heat power is defined by:
with
-
n is the multiple of standard deviation for the chosen confidence interval,
-
ΔPs the uncertainty in decay heat from fission products, and
-
ΔP/P is the uncertainty of relative thermal power.
“The other contributions to the decay heat power PB, PA, PCs, and PE shall be determined conservatively and therefore do not enter into the calculation of the error bandwidth. Using the approximate methods of this document for these contributions results in conservative estimates of the total decay heat power. Alternative methods, such as those based on comparisons of code predictions and isotopic measurements for the main nuclides contributing to each of these decay heat terms, shall be specified, and justified by the user”.
 |
Fig. 27. Top: comparison of the data presented in Table 16 (dashed lines are the values from the code 1 to 5). Bottom: Comparison for the standard only, with both irradiation histories. |
 |
Fig. 28. Total and electromagnetic decay heat component for pulse irradiation of 235U (top) and 239Pu (bottom) with thermal neutrons. |
6.3.7. Example of application
The standards described in the previous sections can be applied to a large number of cases (see for instance Ref. [55]). They can nevertheless lead to different estimations of decay heat and it is of interest to present an example for a specific SNF case. To facilitate the comparison of decay heat values from standards, some simulation codes automatically include standard decay heat values during depletion calculations (e.g. the SNF code). Additionally, to help compare values within this community, Studsvik made available for all SG12 participants a simplified version of the SNF code, allowing them to calculate, with the same input definition, decay heat values for four standards, as presented in Table 16 for the example of the assembly 0E2. At the time of writing, this code is available from the SG12 webpage [8].
A specific example is presented in the following, extracted from the Clab data presented in the 2006 report [76]. The assembly named 0E2 corresponds to a PWR 17×17 assembly with 3.10% enriched 235U fuel, and its burnup is reported at 41.6 MWd/kgU. The full description can be found in the report, together with the value of one measurement, at a cooling of 5823 days (almost 16 years). Five other measurements were later reported in reference [79], for cooling time between 17 to 22 years. Measured and calculated values from the standards are reported in Table 16.
For these cooling periods, the important contributors to the decay heat are fission products, i.e 137mBa/137Cs and 90Y/90Sr (almost 65% in total), and also 244Cm (10%), 238Pu (10%), and 241Am (another 10%). The remaining parts originate in 240Pu and 154Eu. Therefore, given the similar cooling periods, these 6 measurements are helping to validate the same nuclides. Table 16 presents values from dedicated best estimate calculations (called “code 1” to “code 5” to keep anonymity), partly performed by different laboratories using different nuclear data libraries. Such calculations are very close to the measured values, and well within the reported experimental one-standard deviation. Regarding the application of the standards, two sets of histories are used: one simplified and one more detailed. Both sets can be accepted as corresponding to a good representation of the realistic irradiation history. If one first considers a single history (number 1 or 2), it can be observed that the values provided by the four standards present a large spread, larger than the one from the best-estimate calculations. As expected, three standards are conservative, and one (the DIN standard) is closer to the experimental values (see Fig. 27 top). Differences between standards are still noticeable, especially given the experimental and standard uncertainties. This example illustrates that standard values are not systematically coherent between themselves and are generally conservative (except for the DIN standard, but the conservatism is not systematic, as presented in Ref. [55]). The impact of the irradiation history (and the underlying assumptions) is also not negligible, changing the calculated values by more than 5%, as presented in Figure 27 bottom. A dedicated discussion is out of the scope of this work, but the following remarks can be made for this example:
-
Standard values can be sensibly different compared to the ones from best-estimate codes.
-
Standard values are in general more conservative.
-
Standard values can disagree between themselves.
-
As for best-estimate calculations, standard values are sensitive to assumptions made in simplified irradiation histories.
6.4. Summation and best estimate methods
6.4.1. Summation method
Decay heat (rate) is a unique characteristic for any given nuclide composition of nuclear fuel and in general of radioactive matter. The decay rate (or activity) of a radioactive nuclide i is the product of its number density Ni and its decay constant λi. Multiplying the decay rate λi ⋅ Ni by the recoverable energy ei released as radiation during the decay process gives the decay heat rate contributed by that nuclide,
Then, the total decay heat rate H is given by the sum of each individual contribution
hence the name summation method. Among the different methods to model the decay heat of radioactive nuclear fuel after shutdown, the summation method is considered the most general and comprehensive. Despite being widely accepted and adopted in the earliest nuclear applications especially, for crude predictions of the order of magnitudes in short-term decay heat analysis, simple semi-empirical formulations such as those proposed in the previous section have been generally nowadays superseded by the summation method [144]. The completeness of this method stems from explicitly considering the contributions of all nuclides involved in the decay process, including actinides in the nuclear fuel, fission, and activation products. Despite its simplicity, an accurate knowledge of a large number of nuclear parameters (decay constants, beta-electron, and gamma-ray energies) is required.
Given the radioactive nature of nuclear fuel, its decay heat rate inevitably varies with time according to the nuclide content evolution in the system. For reactor spent fuel it decreases following the time after shutdown, as the majority of the short-lived fission products decay into longer-lived ones. It follows that the accuracy of the summation method strictly depends on the correct solution of the Bateman equations. This step is generally considered more crucial than the summation calculation, as the complexity of the process increases when the fuel is placed in an irradiating environment.
The radioactive decay law formulated in 1902 by Ernest Rutherford and Frederick Soddy [145] indicates that the density variation dN(t)/dt of radioactive matter is proportional to its activity. Here, N(t) is the nuclide field vector containing each ith nuclide number density. In his publication at the beginning of the last century [146], Henry Bateman reported the analytical solution of this set of equations considering only natural decay and under the assumption that only the first nuclide in the decay chain had non-zero density.
Still, the concept can be generalized for radioactive matter placed in a particle-irradiating environment by adopting effective reaction rates (or simply reaction rates) that take into account the transmutation caused by particle-nucleus interactions. Each ith ordinary differential equation (ODE) describes the time-balance of a nuclide i as
where
-
Ni, Nj are the number densities of nuclides i and j, respectively,
-
λi, λj are the decay constants of nuclides i and j, respectively,
-
bj → i is the decay branching ratio for a nuclide j to produce nuclide i,
-
⟨σp, i⟩ is the spectrum-averaged Doppler-broadened disappearance cross-section for nuclide i induced by particle p,
-
⟨σp, j → i⟩ is the spectrum-averaged Doppler-broadened cross section for nuclide i induced by particle p and that generates nuclide j,
-
ϕp is the energy-integral of the flux for particle p, being either neutrons, protons, or other particles5.
The spectrum-averaged cross-sections are
where the energy distribution of the particle flux, i.e. the particle spectrum, is denoted by φp(E). The production rate includes all reactions r with cross-section σp, j, r(E) with a non-zero yield γp, j → i, r(E) that generates the nuclide i of interest. If nuclide i is a direct fission product and nuclide j is an actinide, r represents the fission reaction and γp, j → i, r(E) corresponds to the independent fission yield. An independent fission yield is defined as the fraction of a specific nuclide produced directly from a single neutron-induced fission event of a given parent nuclide after the emission of prompt neutrons and gamma rays and before the radioactive decay of the fission fragments.
The particle flux field, normalized to the requested power production, follows the time-dependent neutron transport equation (see Ref. [147]) and is nonlinearly coupled to the calculation for the nuclide vector.
From the above description, the accuracy of the summation can depend on various approximations performed during the irradiation (see next sections), and also on the quality of nuclear data (see Sect. 6.4.3).
6.4.2. Case specific approximations
The transmutation or decay of fission products with large absorption cross sections or in general of strong neutron absorbers can significantly affect the spatial and energy distribution of the neutron flux on a time scale on the order of hours to days [148–150]. The buildup and depletion of actinides have an analogous effect on a longer time scale. Modifications of the irradiation conditions (e.g. reactor power, control rod position, soluble boron concentration) also alter the neutron flux. The dependence of the flux distribution on the nuclide composition is handled in burnup codes by decoupling the neutron transport calculation from the nuclide depletion problem, exploiting the slow variations of the neutron flux distribution (energy distribution as well as spatial distribution) in short time-scales. A quasi-static version of the space and energy-dependent burnup equations assumes static flux distribution that can be computed at the beginning of the time interval of interest by a deterministic or Monte Carlo-based particle transport solver. Then, this flux distribution and the resulting spectrum-averaged cross sections are used to integrate the depletion equations over the time interval for which the transition matrix can be assumed constant. This methodology reduces a nonlinear process into a series of equations that appear to be linearly coupled at given time instances.
There is a number of approximations, both physical and computational, that need to be applied when the burnup calculation is run. Computational approximations include discretization applied to space and time, i.e. depletion zone division and the number of depletion steps, as well as the burnup algorithm used for obtaining the coupled solution by iteration.
Physics approximations are related to the models used for the interaction physics. For deterministic transport codes this includes, for example, the methods applied for self-shielding, and for Monte Carlo codes the treatment of cross sections in the unresolved resonance range and the elastic scattering kernel. Some approximations, such as the definition of energy released per fission and the handling of fuel temperature distributions, result from simplifications in the computational model. The most significant uncertainties in burnup calculation, however, typically originate from the nuclear data libraries used in the calculation (see Sect. 6.4.3).
Spatial discretization
Because of the large costs in terms of computational power and memory necessary to run SNF depletion calculations for LWRs at the core level, a number of customary practices are nowadays accepted by the nuclear industry to reduce the computational running time, such as:
-
Scaling down the core geometrical model to the assembly level with imposed boundary conditions,
-
using a two-dimensional (2D) model,
-
using a discrete number of depletion zones within the assembly,
-
and using a discrete number of depletion zones within the pin.
The two last assumptions include grouping the depleted materials into homogeneous sub-regions, or depletion zones, inside which the reaction rates are assumed space-independent. If the spatial discretization is not carefully defined the local reaction rates may be under/over-estimated in regions where the neutron flux gradients are steep. This is a condition that typically occurs in presence of high-absorbing materials or at the core boundaries. Refining the spatial sub-division reduces the discretization bias, but in practice the total number of depletion zones is limited by the available computer capacity.
Assembly model
To simulate the depletion of nuclear fuel in a fuel pellet, rod or fuel assembly (FA), computational models focus/extend up to the assembly boundaries. The rest of the core is defined by imposed boundary conditions. The first reason is computational time memory and resources: because of the large costs in terms of computational power and memory necessary to run SNF depletion calculations for LWRs at the core level. A second reason is that in many SNF-related benchmarks operational data are only provided on the reference assembly selected for the experimental campaign, whereas details on the adjacent assemblies are not documented [151, 152]. The assembly shuffling is often not simulated when analyzed samples are taken from interior fuel rods as the impacts of neighboring assemblies on the nuclide contents in such rods were shown to be small after 148Nd normalization, see for instance reference [153]. On the contrary, it has been shown that for fuel rods at the periphery of an FA or if the reference FA is located at one edge of the core, modeling the FA surrounding environment has a significant impact on the accurate prediction of nuclide compositions as a function of burnup [154]. Under these conditions a more accurate representation of the rod environment is achieved by including the adjacent assemblies in the simulation model [155, 156].
The down-scaling of the core model to a single assembly (or group of assemblies) is an acceptable approximation as long as the spatial boundary conditions are representative of the assembly position in the reactor core and evolve according to the fuel in-core reshuffling scheme. For instance, the use of reflective boundary conditions along all directions corresponds to an “infinite system”, which is correct if the neutron flux does not have a spatial gradient for several neutron mean free paths from the domain boundaries. Reflective conditions corresponding to a unitary albedo β = 1 (i.e. the ratio between the neutron currents entering and leaving the FA) preserve the neutronics environment of the reference assembly and they are commonly used to represent a FA surrounded by fuel with the same level of burnup [152]. Other albedo boundary conditions are needed when a change of the surrounding media is expected to take place (i.e. around reflectors or strong absorbers such as control rod). Boundary conditions with albedo β > 1 can be representative of an FA surrounded by fuel with lower burnup or higher enrichment. On the other hand, β < 1 is found for assemblies adjacent to moderator channels or reflectors. It is actually common to find this strategy along in-core fuel management depletion calculations of commercial reactors in well established codes like CASMO-SIMULATE and PHOENIX-POLCA. The constraint in defining a certain type of boundary condition might have an impact on decay heat predictions and it is tightly connected to the computational approximations introduced with a spatial discretization.
Radial depletion zones
The spatial dependence of the depletion in equation (62) is typically approximated by adopting a discrete number of volumes (or depletion zones) in which the model is homogenized. Then, for each depletion zone, a set of ODEs is defined using spatially-averaged reaction rates. If the spatial discretization is not carefully defined the local reaction rates may be under/over-estimated in regions where the neutron flux gradients are steep.
The volume subdivision should be physically driven by the system heterogeneities and by the spatial distribution of the neutron flux, e.g. at the model boundaries or in presence of high-absorbing materials. In an FA, depletion zones could follow the pin cell boundaries or include several adjacent pins. In general, a trade-off is sought between the computational time and the representativeness of the mode, knowing that refining the spatial sub-division reduces the discretization bias. In particular, in Monte Carlo burnup codes the smaller the depletion zones are the longer it takes a transport calculation to achieve a reliable estimate of the reaction rates.
In a FA model the flux distribution is affected by the type of applied boundary conditions. Reflective boundaries along all directions (i.e. β = 1) define an infinite medium with the nonphysical suppression of neutron leakage. Under these circumstances, it is foreseeable that a limited number of depletion zones could correctly reproduce the nuclide buildup in the system, as the neutron flux distribution is approximately flat. Conversely, white boundary conditions in all directions (i.e. β = 0) impose a steep gradient to the flux and more burnable zones should be used.
A volume discretization based on physical metrics such as the neutron flux or burnup spatial gradient can produce optimal results when it comes to accurately predict the nuclide content in SNF. This is particularly true for nuclides such as 134Cs, 241Am, and the curium isotopes whose concentrations do not evolve linearly with burnup. The same conclusions hold for decay heat calculations. Adopting a single depletion zone appears to be a reasonable option only in case of reflective boundary conditions, or for medium-term cooling times, where the most of the decay heat is released by the decay chains of 137Cs and 90Sr, two nuclides whose concentration in SNF is almost linearly dependent on burnup in the case of LWR.
2D vs. 3D
At the beginning of life, the axial distribution of the neutron flux in a LWR FA approaches a cosine, with the neutron leakage being responsible of the flux depression at the vertical extremities of the assembly. Spectral effects generally occur in the same regions and depend on the core configuration above and below the fuel, e.g. presence of cladding, structural components, fertile fuel, axial blanket, coolant. An uneven axial flux distribution depletes the fuel at a higher rate near the axial midsection than at the ends. During operation, the burnup buildup decelerates at the center because of the accumulation of fission products and the depletion of the fissile material [157–160]. The burnup axial profile in a fuel assembly at discharge is relatively flat in the axial center with burnup peaks 1.1-fold the assembly average burnup, and considerably low at the extremities, down to about half the assembly average burnup [161]. In addition, the higher moderator density in the FA bottom half typically generates an axial offset with a higher burnup towards the bottom of the fuel assembly compared to the top. Some assemblies might display a different offset due to the proximity of control rods during their operational history, although this effect should in principle disappear at the time of discharge [158].
Bounding burnup axial profiles have been established for the criticality calculations of commercial LWR assemblies to maximize the effects that the low burnup regions near the ends of spent fuel have on the system reactivity, i.e. so-called “end effect”. However, such profiles do not ensure a conservative generation of the spent fuel nuclide concentrations with respect to decay heat applications. For example, using non-irradiated fuel is a conservative assumption for reactivity calculations, but not for decay heat predictions [162].
An accurate determination of the burnup accumulated axially in the fuel removes biases in the decay heat estimates that are otherwise introduced with simplified modeling assumptions. A typical approach to predict SNF integral quantities such as the decay heat rate of a FA implies using two-dimensional (2D) lattice models, with corrections to account for the axial flux variation [163]. On the other hand, despite burnup codes coupled to 3D transport solvers can accurately model the flux profile, often simplifications are introduced, either to reduce the complexity of the system or for lack of information on the operating conditions [164]. Parameters such as the material composition, temperature, and density in the FA are often homogenized to an average value, under the assumption that they have a linear dependence with the observable of interest.
The parametric study reported in reference [165] for a reference PWR FA assembly model (with an initial enrichment of 3.1%, and an average burnup of 36.7 GWd/tHM) shows that the decay heat rate does not scale linearly with modeling parameters such as the moderator temperature at long cooling times and the cycle power at shorter cooling times (see for instance Ref. [166]).
Time discretization
Despite the latest enormous development in computer technology, depletion codes coupled to Monte-Carlo transport solvers are still considered computationally expensive, primarily because of their more and more frequent application to complex realistic problems such as a whole fuel assembly or a full-core problem. The most common solution adopted to reduce the computational burden is to introduce approximations in the coupled problem. In Monte Carlo burnup codes the solution for the neutron flux field tends to be more computationally expensive than the integration of the depletion equations. Hence, the time steps for complex problems are generally long in order to minimize the number of steady-state neutron transport calculations. Although the neutron flux field generally varies in time at a lower rate compared to many nuclide number densities, a coarse time-discretization might lead to an under- or over-estimation of the reaction rates at which individual nuclide concentrations are built up or depleted. This can result in significant discretization errors. Time-dependent spectral variations within a time step can be accounted for by using predictor-corrector algorithms, with a considerable improvement in the accuracy of the burnup solution [167, 168]. It was demonstrated that the use of implicit predictor-corrector algorithms such as the modified Euler method can also prevent stability issues, e.g. spatial oscillations of the neutron flux driven by the neutron capture in 135Xe or, for longer time steps, by the fuel burnup [148, 169]. Adopting advanced burnup algorithms with reaction rate interpolation/extrapolation capabilities can overcome the bias introduced by longer time-steps. Then, the time-dependence of the transition matrix in a depletion time-step can either be inherently handled by the ODE solver [170] or by further dividing the time-step into a number of sub-intervals [171, 172].
Shortening the time steps reduces the bias on the burnup solutions, but since the total number of depletion steps is increased, so is the overall computational cost. The optimal time-step length is problem-dependent and, as a rule of thumb, it increases as the irradiated material is depleted. Numerical tests suggested that the computational efficiency of Monte Carlo burnup calculations might be actually improved by shortening the time steps and running transport calculations with a larger statistical uncertainty [173]. Following these results, algorithms are being developed to maximize the efficiency of the Monte Carlo burnup simulation by optimizing the time-step length [174].
DBRC
The scattering of neutrons in the epithermal energy range can be significantly affected by thermal motion of target nuclides [175]. The probability of change of a neutron’s initial energy and direction as a consequence of an interaction with a target nucleus (i.e. sampling the scattering kernel) is traditionally simulated in MC codes in reference [176]: (i) using a free gas model or pre-processed thermal neutron scattering kernel tables S(α, β) considering internal changes in the molecule (crystal effect), in the thermal energy range; (ii) sampling the target nuclide velocity from a Maxwellian distribution in the epithermal energy range; and (iii) assuming the target to be stationary at sufficiently high neutron energies (400 kT).
While the traditional approach in the epithermal energy range is valid for light nuclides, heavy nuclides, in particular 238U, should include the fact that the cross section is definitely not constant in the vicinity of the resonances [177]. To take this effect into account, resonant dependent probabilities (i.e. S(α, β) tables) for heavy nuclides were introduced [178]. However, this method is limited since the anisotropy of the azimuth angle between the interacting plane and the scattered neutron plane is not considered, and this is needed for the accurate handling of the scattering kernel [179]. Alternatively, Rothenstein [180] proposed a re-write of the elastic scattering probability density function, which is suitable for numerical calculations, and that it is implemented in state-of-the-art neutron transport codes such as MCNP [181], KENO [182] or SERPENT [183] to account for non-constant scattering cross sections.
6.4.3. Nuclear data
Nuclear data provide important quantities for the calculation of decay heat following the summation method. Precise information on cross sections (e.g. fission and capture), decay data (such as half-lives, released energies, branching ratios) or fission yields are needed if one needs to rely on calculated decay heat. Over the past decades, there have been numerous improvements from the nuclear data libraries (improved cross sections, fission yields, decay data), supported by a large range of validation, leading to more accurate summation calculations. Comparisons between various current nuclear data libraries are presented in Figure 28, for the total and decay heat (electromagnetic component) of 235U and 239Pu thermal fission pulses.
The experimental values and calculations presented in this figure are obtained from references [58, 107, 122, 124]. Such better agreement between calculations, based on the improvement of nuclear decay data along the years, and experimental values provide confidence in the results from the summation method for SNF.
A detailed study on the need for nuclear data related to decay heat can be found in references [184] and [7]. From equation (62), one can see that the quality of the nuclear data directly affects the estimation of the nuclide concentration, and therefore of the calculated decay heat. As an example, the improvement of the decay heat calculations thanks to the TAGS data (see Sect. 6.4.4) was highlighted in many references (see for instance Refs. [185–187]). The quality of fission yields (cumulative as well as independent) also plays a prime role in the estimation of nuclide concentrations. Figure 29 presents two examples of cumulative fission yields, before and after irradiation of two UO2 and MOX assemblies in a realistic core environment.
 |
Fig. 29. Example of weighted cumulative fission yields, before and at the end of irradiation, for two UO2 and MOX assemblies. |
These examples highlight the changes of the so-called “double-hump curve” with burnup, and indicate the variety of nuclides to take into account to obtain an adequate SNF characterization.
6.4.4. TAGS data
Pandemonium effect
Decay heat calculations are based on summation calculations performed with evaluated decay data, as explained in Section 6.4.1. The average β− and γ-ray energies released per decay ( ,
,  ) are obtained from the individual beta decay schemes of the decaying fission products using the Iβ− feeding to each individual state in the daughter nucleus and their discrete γ-rays energies. Usually, the Iβ− intensity distributions are obtained from high-resolution spectroscopy measurements with Ge detectors based on the γ-ray intensity balance technique which relies on the detection of all individual γ-rays coming from the levels fed in the β− process and their placement on the beta decay level scheme. This technique suffers from a well known systematic error called Pandemonium effect pointed out by Hardy et al. in1977 [188].
) are obtained from the individual beta decay schemes of the decaying fission products using the Iβ− feeding to each individual state in the daughter nucleus and their discrete γ-rays energies. Usually, the Iβ− intensity distributions are obtained from high-resolution spectroscopy measurements with Ge detectors based on the γ-ray intensity balance technique which relies on the detection of all individual γ-rays coming from the levels fed in the β− process and their placement on the beta decay level scheme. This technique suffers from a well known systematic error called Pandemonium effect pointed out by Hardy et al. in1977 [188].
 |
Fig. 30. Schematic picture of the Pandemonium effect. |
 |
Fig. 31. Left: light particles decay heat component for pulse irradiation of 235U with thermal neutrons. Right: same for the electromagnetic decay heat component. |
 |
Fig. 32. Left: light particles decay heat component for pulse irradiation of 239Pu with thermal neutrons. Right: same for the electromagnetic decay heat component. |
Using a fictional nucleus called Pandemonium with a complex decay scheme, Hardy et al. showed that 14% of the γ-ray intensity above 1.7 MeV remains undetected under normal experimental conditions using a Ge(Li) detector. Due to the limited peak efficiency of Ge detectors, some γ-ray transitions from levels at high excitation energy are missed and consequently extra β− feeding is incorrectly assigned to low lying states, shifting the apparent Iβ− distribution to lower excitation energies, see Figure 30. This leads respectively to an under-estimation of the γ-ray and over-estimation of the β− energies released in the decay. The largest effect is observed in the decays with large Qβ− values because the level density increases with the excitation energy (providing many possible weak γ decay paths that can remain undetected) and those where the β− strength concentrates close to the end of the Q-value energy window [189].
Total Absorption Gamma-ray Spectroscopy technique
A different experimental technique, the Total Absorption γ-ray Spectroscopy technique (TAGS), based on the detection of the full γ-ray cascades which follow the β− decays instead of detecting the individual γ-rays was developed to overcome the Pandemonium effect. This technique relies on a large detection efficiency of γ-rays, almost 100%, which is usually obtained with large scintillator crystals with a geometry as close as possible to 4π. In the 1990s, a total absorption γ-ray spectrometer coupled to a 252Cf-based ISOL facility was used in a program of systematic study of the distributions of β− decay intensities of fission products by Greenwood et al. [190] aiming to improve decay data needed for decay heat calculations. Results were obtained for 48 nuclei on Rb, Sr, and Y isotopes and the region of Z ≥ 55, with half-lives ranging, generally from more than 5 seconds to less than a few hours. Twenty-nine nuclei had their mean decay energies updated in the JEFF-3.1.1 library using these measurements. The nuclei updated, see Tables D.1 and D.2 (in Appendix D), were only those for which a detailed evaluation was not available [191]. No details were given on the analysis and a conservative 10% uncertainty was applied to all mean energies. The evaluation of these nuclei was also taken into account for the release of the ENDF/B-VII.1 library in 2011. Since then, the analysis methodology of the TAGS technique was considerably improved, especially by the Valencia group (see Refs.[192–195]).
In 2005, a WPEC Subgroup 25 was focused on the assessment and improvement of the evaluated decay data sub-libraries in order to obtain more accurate estimations of decay heat [7]. Recommendations were made to focus on a list of 37 particular fission products that merit measurement by TAGS in order to improve decay heat calculations. Consultant’s meetings were also organized afterward by the Nuclear Data Section of IAEA to improve/complete the initial list of proposed TAGS measurements for decay heat both for U/Pu and Th/U fuel cycles but also for other possible applications associated with the determination of antineutrino spectra in reactors and the study of beta-delayed neutron emitters [196–198]. The meetings also monitored the progress of the different experimental campaigns and their impact. Four experimental campaigns were performed in 2007, 2009, 2014, and 2022 by the European TAS collaboration (CSIC-University of Valencia) Spain and the University of Surrey, UK, joined by the SUBATECH team, Nantes, France in 2009) at the IGISOL facility in Jyväskylä, Finland (see Refs. [199–206]). TAGS experiments were also performed on nuclei from the NEA list at the Holifield Radioactive Ion Beam Facility at the Oak Ridge National Laboratory by the MTAS collaboration (USA, Poland)[207–209]. Tables D.3 and D.4 (Appendix D) list the nuclei that were measured and published by the different teams up to now from the NEA list. The gray cases are the TAGS  and
and 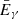 already evaluated and included in the JEFF, JENDL, and ENDF libraries as ELP and EEM values. It should be noted that 102Tc and 101Nb were not included in JEFF-3.3 from the European TAGS measurements because the mean decay energies were almost identical to the values already in JEFF-3.1.1 for the first one and for the second one there was almost 50% uncertainty on the mean gamma-ray energy [191]. These cases were shown to not suffer from the Pandemonium effect(see Refs. [199, 200]).
already evaluated and included in the JEFF, JENDL, and ENDF libraries as ELP and EEM values. It should be noted that 102Tc and 101Nb were not included in JEFF-3.3 from the European TAGS measurements because the mean decay energies were almost identical to the values already in JEFF-3.1.1 for the first one and for the second one there was almost 50% uncertainty on the mean gamma-ray energy [191]. These cases were shown to not suffer from the Pandemonium effect(see Refs. [199, 200]).
Impact on fission pulse decay calculations
Recently, some decay heat calculations of the Light Particle (LP) and Electromagnetic (EEM) components both for 235U and
239Pu thermal fission pulses were performed using the Serpent code [183] to calculate the impact of the TAGS measurements already included in the JEFF, JENDL,
and ENDF evaluated libraries [210]. Decay heat calculations based on different releases of the JEFF library are compared in Figures 31 and 32 with the Tobias evaluation, Dickens, and Lowell decay heat measurements [107, 122, 124]. The decay heat calculations for the thermal fission pulses of 235U and 239Pu obtained with different versions of the series of JEFF libraries in their chronological order illustrate clearly the growing impact of the TAGS measurements with a decrease in the LP and an increase in the EEM decay heat components. This is a direct consequence of the adoption of Pandemonium-free decay data.
Decay heat calculations were also performed on thermal fission pulses in order to compare the performance of the latest evaluated libraries: ENDF/B-VIII.0 [211],
JEFF-3.3 [58], and JENDL-5 [212]. The decay heat curves for the Light Particle component, both for
235U and 239Pu thermal fissions, are in good agreement with the decay heat measurements and their experimental uncertainties. The electromagnetic decay heat component of 235U thermal fission from 2 to 100 seconds cooling times is underestimated per the JEFF-3.3 calculation whereas both ENDF/B-VIII.0 and JENDL-5 calculations agree. At cooling times above 400 seconds, it is rather difficult to conclude as the three sets of measurements exhibit discrepancies that remain unresolved at this stage. For the electromagnetic decay heat component of 239Pu, the peak at cooling times from 30 to 200 seconds is overestimated per the JENDL-5 calculation. Given the importance of 239Pu thermal fission for decay heat, further investigations were performed by repeating the same calculation using the JEFF-3.3 decay data library combined with three different fission yield libraries: ENDF/B-VIII.0, JEFF-3.3 and JENDL-5. As shown in Figure 33, both calculations performed with the ENDF/B-VIII.0 and JEFF-3.3 fission yield libraries reproduce the experimental data whereas the adoption of the JENDL-5 fission yield library leads similarly to an overestimation of the decay heat measurements in the 30–200 seconds cooling range. This overestimation would appear to be associated with the fission yield library and is now studied in detail per the JENDL team with respect to a release of fission yielddata [210].
 |
Fig. 33. Impact of fission yield libraries on electromagnetic decay heat component for pulse irradiation of 239Pu with thermal neutrons. |
6.5. Methods for depletion solvers
The analytical solution of the Bateman equation is the matrix exponential function:
where n(t0) is the nuclide density vector at time t0. The part of the transition matrix A representative influencing the natural decay or the neutron-induced activation of a given nuclide usually contains reaction rates for only a few dozen of nuclides. On the other hand, the time evolution of the fuel composition in a nuclear reactor requires already 30–40 fission products and actinides that characterize the major SNF observables. In addition, several of these nuclides are generated via the decay or neutron-capture processes involving other nuclides, thus extending the list to several hundreds. Eventually, if one wanted to consider all nuclides for which nuclear data are provided in the evaluated radioactive decay data libraries, the number would increase to almost 4000, e.g. the JEFF-3.3 radioactive decay data library provides data for 3852nuclides.
The exponential of a matrix can be computed in many ways involving different approximations [213], still in a transmutation-rich environment their implementation is not straightforward and requires to take into account the following considerations:
-
half-lives (T1/2 = log(2)/λ) can vary from billions of years to small fractions of seconds, thus generating a large spread in the transition matrix eigenvalues and making the system numerically stiff;
-
the large decay constants associated with highly unstable nuclides (e.g. 7B with a half-life T1/2 of about 10−22 seconds) make the problem ill-conditioned, with a matrix norm up to ||A|| ≃ 1021;
-
long time steps also drastically increase the conditioning of the problem.
The main challenge in solving the depletion problem lies not in the mathematical form of the Bateman equations governing the changes in the nuclide concentrations, but rather in the large dimensions and the numerical characteristics of the system. In practice, however, there exists a wide range of state-of-the-art solvers that are capable of handling the depletion problem with a sufficient level of accuracy, and errors resulting from their limitations can be considered negligible compared to other factors. Comparisons of depletion algorithms in terms of performance and numerical accuracy are also reported in references [213, 214]. A number of examples are presented below.
Transmutation trajectory analysis (TTA)
The TTA method [215], also called the linear chain method, implies the analytical solution of one Bateman set of equations per each individual transmutation chain. The time evolution of the nuclide vector is broken down into chains that represent every possible reaction path. This method is used also for non-linear chains after they have been broken down into sets of linear chains. The total nuclide number densities are obtained from the sum of the results of each sub-chain for all the nuclides involved in the problem. Examples of codes that use this method are BISON [216], CINDER [217], MCB [218, 219], and Serpent [183].
The depletion of nuclear fuel involves an enormous network of complex sub-chains that often happen to generate loops that cannot be linearized. As a consequence, assumptions are made to terminate unimportant chains based on multiple criteria, such as ignoring cyclic chains or terminating them after the first few loops. The choice of the termination criterion can play a role in the trade-off between computational speed and accuracy.
Matrix exponential methods
The solution of the Bateman equation can by definition be formally expanded as the Taylor series of the matrix exponential:
The matrix exponential method includes an approximation of the matrix exponential by a truncated Taylor series. This is implemented in the depletion code ORIGEN, available in the SCALE suite [220, 221], and adopted in many coupled neutron transport and fuel depletion codes (see for instance Monteburns [222], MOCUP [223], MCODE, ACAB [224], EVOLVOCODE [225] or VESTA [226]).
The ORIGEN method involves solving the matrix exponential in three phases, in which the contribution of short- and long-lived nuclides is separated. The short-lived nuclides initially present at time t0 in the nuclide vector are treated independently by constructing for each nuclide all the populating chains consisting of only short-lived nuclides and solving them in a way analogous to the TTA method. In the second phase, the contributions of short-lived nuclides to long-lived nuclides are added to the initial densities of the latter. The transition matrix A is then re-constructed by assuming that the short-lived nuclides decay instantly, thus practically removing them from the system. By having removed the instabilities associated with short-lived nuclides, the matrix exponential can now be solved by using a power series. Eventually, the contributions of long-lived nuclides to short-lived nuclides are obtained iteratively using the results of the second phase as an initial guess and assuming a secular equilibrium
valid for short-lived nuclides.
Ordinary Differential Equation Methods
The Bateman equation adopted to describe the time evolution of nuclear fuel composition in a reactor is a system of ordinary differential equations (ODE), therefore it is natural to consider its resolution via numerical integration methods [227]. Ready-to-use packages of ODE solvers [228] are nowadays distributed for the most common computer programming languages.
Among the codes that rely on such methods, there is ALEPH-2 [229], which uses the RADAU IIA implicit Runge-Kutta method of order 5. This method, as well as others involving numerical integration, is easy to use and requires only minimal programming for its implementation. RADAU IIA showed excellent stability for systems containing 3000 and more known nuclides, with the primary disadvantage being the relatively high cost in computer time compared to other solvers like ORIGEN. Still, these methods have been often developed for general nonlinear differential equations, and could potentially achieve much shorter running times if optimized for specific ODE problems.
Other numerical integration schemes (Runge-Kutta, BDF) could be considered for depletion calculations, but are limited by the nuclides with short half-lives that make the problem stiff. Such methods could be used if the short-lived nuclides were handled separately as done by ORIGEN. This is the case of the newest depletion module PHOENIX included in VESTA [226], which solves the Bateman equation either with a fourth-order Runge-Kutta method, a Taylor series development of the matrix exponential or the method of Arnoldi [230], after the separate treatment of the short-lived nuclides.
Chebyshev rational approximation method (CRAM)
CRAM is a method to solve the matrix exponential equation that is implemented e.g. in Serpent [183]. It involves approximating the exponential function ez as a ratio between two polynomials Pk(z) and Qk(z) of order k:
Eventually, the solution of the Bateman equation can be retrieved from solving k/2 linear systems using LU decomposition. The main advantage of this method is that for a chosen polynomial order k and range of values z, the coefficients of the polynomials Pk and Qk need to be determined only once. This method has been proven particularly effective for sparse matrices and, with order k = 16 polynomials, it can provide very accurate solutions to burnup equations without excluding any nuclides. More details can be found in reference [231].
6.6. Sources of uncertainties
As for many other calculated quantities based on reactor simulations involving neutron transport and thermal-hydraulics modules, the assembly decay heat can be affected by various parameters. Additionally, such parameters may not affect the calculated decay heat in the same way as a function of cooling time. For instance, quantities of relevance during (or just after) reactor transients may not be the same as for long-term cooling. As it is challenging to be exhaustive within this study, we will provide a number of examples, mostly for cooling time longer than months after shutdown.
Quantities of relevance, being significant sources of uncertainties for the assembly decay heat are generally classified into different groups: nuclear data, operating conditions, manufacturing tolerances, and eventually burnup-induced technological changes. A number of values for uncertainties from the literature are presented in Table 17. Details are provided below.
Uncertainties for operational parameters, manufacturing tolerances, and burnup-induced technological changes.
6.6.1. Method of uncertainty propagation
In the case of depletion calculations followed by a cooling period, the method of uncertainty propagation mostly used for such non-linear and time-dependent cases is based on simple Monte Carlo: repeating a number of times the same calculation, but each time with a different set of input parameters. This approach allows to access an estimated probability density function for the quantity of interest, from which the uncertainty can eventually be represented by a standard deviation. Such a method is applicable for decay heat, as well as for any other quantities similarly obtained, such as nuclide concentrations or assembly and reactor quantities. Many publications using this method can be found in the literature. One limitation of this approach is due to the required calculation time, which is virtually multiplied by the number of sampled cases. It is therefore not uncommon to estimate uncertainties based on a few hundred of sampled runs. A number of acceleration solutions exist, depending on the type of transport method used: Monte Carlo or deterministic.
Another method of uncertainty propagation is based on sensitivity calculations, under the linearity assumption, combined with the so-called “sandwich formula”. This method requires to calculate the sensitivity of the quantity of interest to a specific input parameter, and then to perform a matrix multiplication between sensitivity vectors and covariance matrices. If this method is in principle faster than the Monte Carlo uncertainty propagation, it is based on the linearity assumption and can become cumbersome in the case of a large number of input quantities (such as nuclear data).
6.6.2. Nuclear data
The impact of nuclear data on decay heat was presented in a number of publications, see for instance references [12, 33, 34, 52, 165, 233–235, 245, 246]. The usual approach to assess the uncertainties due to nuclear data is to consider the covariance matrices provided in the evaluated nuclear data libraries, generate a set of sampled cross-sections or decay data, and repeat transport calculations with these different nuclear data. As long as covariance matrices are provided, the user is well-guided. In the case of missing information, such as for fission yields, users can apply different methods, effectively leading to different calculated uncertainties.
Nuclear data of importance for decay heat are generally cross sections (fission, capture, for both fission products and actinides) and fission yields (mostly from 235U and 239Pu). Decay data (released energy, decay mode, half-lives) induce uncertainties overall smaller than cross sections and fission yields, but their treatment is less rigorous due to the lack of covariance information in evaluated libraries.
Finally, it can be mentioned that nuclear data is one of the major contributors to the decay heat uncertainties, as generally indicated in the mentioned references.
6.6.3. Manufacturing tolerances
Manufacturing tolerances include uncertainties on the design dimensions of fuel assemblies (such as pin radius, pitch, and cladding thickness), on the fuel density, on the initial heavy metal contents (uranium, plutonium and eventually americium isotopes) and possibly neutron absorber contents (such as gadolinium isotopes). Their impact is not negligible, as shown in the previously mentioned references.
Initial geometry and density uncertainty
The proper evaluation of decay heat rates requires the selection of appropriate input uncertainties of stored FA in the Spent Fuel Pool and density uncertainties. For example, if the fuel is provided in the form of cylindrical pellets, the equation could be applied accounting geometrical and density uncertainties: 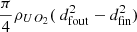 , where dfout, dfin, ρUO2 and l are the outer column diameter, inner column diameter (if exists), density, and fuel length, respectively. The fuel column length could be the total reactor core length or the individual fuel pellet. As the column length uncertainty range, due to vendor procedures compensating the other geometrical uncertainties, then it is not accounted for in this section. An example of VVER-1000 fuel pellet uncertainty ranges is provided in Table 18 [247, 248].
, where dfout, dfin, ρUO2 and l are the outer column diameter, inner column diameter (if exists), density, and fuel length, respectively. The fuel column length could be the total reactor core length or the individual fuel pellet. As the column length uncertainty range, due to vendor procedures compensating the other geometrical uncertainties, then it is not accounted for in this section. An example of VVER-1000 fuel pellet uncertainty ranges is provided in Table 18 [247, 248].
Example of VVER-1000 nuclear fuel uncertainty ranges.
The analytical estimation of the geometry uncertainty generated the following equation (69):
The description of the symbols, used in equation (69) is given in Table 18. In the case if no internal opening exists in fuel pellets by the design, then Δdfin = 0. The uncertainty range is technologically bounded within the following limits: m − Δm1 ≤ m ≤ m + Δm2, where the particular absolute mass uncertainty could be evaluated based on data from Table 18. In this particular case, the lower and upper portions of the FA mass uncertainty range have different sizes, which indicates a non-symmetrical statistical distribution, due to the vendor’s production of technological geometrical uncertainty ranges (provided in Tab. 18). However, for other types of fuel made by the same or other vendors, this analysis could be different.
Fuel mass uncertainty
The fuel mass uncertainty is an added value to the initial geometrical and density uncertainties, based on the operational procedure for the fuel production. The limit could be set so that the total mass should not exceed a threshold, which usually is the nominal value, considered by the fuel column design. In this case, the geometrical uncertainty could be upgraded to m − Δm1, which transforms the original two-sided statistical uncertainty to one side. Therefore, the geometrical uncertainty is reevaluated, according to the fuel vendor procedures, in order to avoid additional non-realistic conservatism.
Enrichment uncertainty
Usually, the enrichment uncertainty is provided by the fuel vendors where the manufacturer’s fuel enrichment uncertainty was considered to have a limit as presented in Table 17. However, during recent years some of the facilities, operating nuclear fuel adopted technology for enrichment evaluation by the use of a compact detector (as an example CdZnTe), which is inserted into the instrumentation channel of the examined assembly and registers the low-energy gamma-ray and characteristic radiation from the isotopes of uranium and their decay products (see Refs. [52, 249]). As an example, the fuel enrichment measurement procedure at the Kozloduy NPP involves the measurement of 185.7 keV peak of 235U. In this particular case, the measurement time is 600 seconds, and the number of counts varies within the range of 5000to 6000.
6.6.4. Operating conditions
Operating conditions of importance for decay heat uncertainties can be numerous, depending on the cooling time of interest: the fuel and moderator temperatures, reactor pressure, boron concentration, assembly power (or burnup), moderator density, and irradiation history.
Power history
The uncertainty in the power of the FAs can be obtained from the analytical core design software. Such software passes extended verification and validation procedures and depending on the results, a qualified uncertainty range is produced (generally in terms of “rms”, or root-mean-square). For example for the VVER-1000 core design software, the burnup relative uncertainty ±δB is evaluated as follows reference [250]:
Moderator density (coolant pressure, temperature)
The decay heat rates can be influenced by the change of characteristics for the moderator, as it was indicated in a number of publications. As indicated in reference [246] for BWR calculations, the moderator density during irradiation has a non-negligible impact on local decay heat, being higher than 1% at 100 years of cooling time. For PWR cases, the impact of the moderator temperature reaches similar values [33].
 |
Fig. 34. Total decay heat generation rate in Kozloduy NPP unit 6, Spent Fuel Pool: (a) 2014-2015 uncertainty evaluation; (b) 2018–2019 uncertainty evaluation; (c) 2014–2015 bounding data; and (d) 2018–2019 bounding data. |
6.6.5. Example: GRS best estimate method uncertainty analysis
This example of evaluation of the output uncertainties of FA decay heat generation rates is based on a method previously proposed by the Gesellschaft für Anlagen- und Reaktorsicherheit (GRS) [251, 252] and is currently applied for some safety analysis. This method allows realistic prediction of output uncertainties, calculated after the evaluation of selected input parameters uncertainty propagation. The selected input parameters are expected to be randomly varied within the defined ranges of their minimal and maximal values. The necessary number of calculations is determined as suggested previously by Wilks [253, 254]: 1 − un − n(1−u)u(n−1) ≤ v for two-sided statistical tolerance intervals. Correspondingly for one side of statistical distribution, the proposed formula is: 1 − u(n−1) ≤ v [253, 254].
The parameter u is compared with the probabilistic acceptance criterion (percentile), while the parameter v is the confidence level that accounts for the influence of the sampling error from a randomly chosen sample of limited size. The formula predicts n = 93 separated calculations with 95% probability for the 95% confidence level for two-sided statistical distribution and n = 53 separated calculations for one-sided statistical distribution. In general, there is no expectation that some values in the input parameters uncertainty ranges are more likely than others. Therefore, usually, uniform probability density functions (PDFs) are assumed, which is a widely accepted choice for this type of calculation. As a result by application of this method, a set of curves is expected to be obtained for the output decay heat generation rate, where the bounding maximal and minimal values form the propagated output uncertainty range. Figure 34 presents an evaluation of the decay heat generation rate in Spent Fuel Storage onsite in Kozloduy NPP (Unit 6, VVER-1000). In the analysis were considered two storing periods: from 2014 to 2015 and from 2018 to 2019. The uncertainty calculations were performed based on the initial geometrical and density uncertainties, combined with power operation uncertainties evaluated using RG US NRC 3.54.
The uncertainty analysis was performed for two FA batches stored in the spent fuel pool. All calculations were based on the procedure provided by US NRC RG 3.54. The described input parameters in section three were varied randomly within their defined uncertainty ranges (see Tab. 18). The set of 98 calculations included n = 93 random combinations of the following parameters: fuel pellet inner diameter and outer diameters, UO2 fuel density, full power effective days, burnup, and nominal operation power uncertainty (Tab. 18 [250]). The results of the calculation indicated that the decay heat rate uncertainty range is sensitive to the variation in the irradiation conditions, initial mass, and type of fuel assemblies, stored in the spent fuel pool. The results are plotted in Figure 34, where the independent variable of the plots is given in logarithmic scale. The conservative approach states a fixed upper bound of values, where a 10% conservatism was assumed, added to the estimated nominal values for the spent fuel pool [255].
These results were verified additionally by SCALE calculation. The evaluation of the uncertainties in the input values and their propagation to the output identifies the ranges of the variation in the overall spent fuel pool decay heat rates.
6.6.6. Alternative approach: safety factor definition
The uncertainties taken into account in the evaluation of decay heat generation rates can be produced by (1) uncertainty in nuclear data, (2) numerical computational models, and (3) inaccuracies from data numerical interpolation and handling of the irradiation history, see for instance reference [28]. These uncertainties are considered by the scaling coefficient and (safety factor) Fs > 1 in this reference. A reasonable amount of conservatism is then applied to the computed decay power values. The approved values of the safety factor in reference [28], derived from calorimetric measurements, are reported in Gauld and Murphy [52]. The uncertainty upper bound, which for instance is estimated numerically by reference [28], lay approximately +6% above the experimental data, without the use of the conservative assumption as a safety factor [52]. Furthermore, Gauld and Murphy [77] recommended a safety factor of 1.02 (maximum +8% uncertainty) for a PWR FA stored less than 25 years. Therefore, the safety factor ensures reasonable conservatism in the evaluation of the decay heat generation rate for a PWR. The decay heat rates calculated by the same authors using ORIGEN, compared with the measured values, produced an uncertainty of 4% [52].
7. Computer codes
In the following, a number of codes used in the estimation of assembly decay heat for LWRs are presented. For details, a number of references are provided in each case.
7.1. CEA computer codes: DARWIN/PEPIN2 and MENDEL
Two major codes devoted to nuclide inventory and decay heat calculation are available at CEA. They solve simultaneous ordinary differential equations describing the transmutation, the growth and the decay of the nuclide densities, and perform an accurate depletion calculation with a fine description of the irradiation history and the isotopic chain. From nuclide concentration results, a large range of physical quantities can be calculated like nuclide mass, radioactivity, decay heat, decays α-particle, β-electron, γ-ray emission, neutron source from spontaneous fission, delayed neutron, and (α,n) reaction. These physical quantities can be computed at any cooling time.
The first of the two codes is DARWIN/PEPIN2 [256] which is a modular code system, which means it is composed of different modules where each of them has specific features. It has been developed and maintained since the mid-90s. In the field of reactor physics studies, it can be linked to CEA neutron transport codes APOLLO2 which provide the necessary neutron data for the nuclide inventory calculation. It implements a numerical fourth-order Runge-Kutta method to solve the Bateman equation for irradiation period, and an analytical solution algorithm for the cooling period. In the irradiation periods, short half-life nuclides are computed apart (considering a saturated state) in order to obtain a faster solving of the numerical system. DARWIN/PEPIN2 code is a part of DARWIN package which is mainly used with APOLLO2 code in a validated calculation scheme for fuel cycle nuclide inventory or decay heat calculations, with consistent nuclear data libraries based on JEFF-3.1.1 evaluation. DARWIN/PEPIN2 is currently the reference code used by the CEA and its industrial partners EDF and FRAMATOME for fuel cycle studies through the DARWIN package.
In recent years, in the consistency of development of both the new generation 2D/3D transport code APOLLO3® [257] and the new nuclear data processing code GALILÉE [258] at the CEA, a new depletion code-named MENDEL has been developed [259]. All of these codes are developed in a modern object-oriented architecture with C++ language, allowing a very strong interoperability between them. For example, MENDEL shares its depletion solver library with APOLLO3® and TRIPOLI-4® [260]. A specific neutron characteristics library named MPO (as Multiple Parameters Output) is provided by transport calculation with APOLLO3® and used by MENDEL for the nuclide inventory calculation. MENDEL implements CRAM (Chebyshev Rational Approximation Method [261]) in addition to the methods also available in DARWIN/PEPIN2 code (RK4 and analytical).
For both codes, once all nuclide concentrations Ni(t) are known, other time-dependent physical quantities of interest (Q.O.I) can be computed: mass, activity, decay Heat, radiotoxicity, α-particle emission, β-electron emission, γ-ray emission, neutron source from spontaneous fission, neutron source from (α,n) reaction, delayed neutron.
At each cooling time t, the total decay heat is derived from the following expression:
where:
-
λi: is the decay constant of nuclide i
-
Ni(t): is the concentration of the nuclide i at cooling time t
-
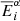 ,
, 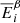 ,
, 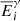 : are respectively the decay energy emitted by α, β and γ disintegration.
: are respectively the decay energy emitted by α, β and γ disintegration.
Q.O.I can be calculated in the three following operating modes:
-
Nuclear reactor fuel depletion followed by cooling period.
-
Neutron activation of material structure followed by cooling period.
-
Cooling of initial radioactive material.
Uncertainty quantification propagating nuclear data uncertainties to Q.O.I (in particular for decay heat) is available in both codes:
-
Deterministic direct first-order perturbation (one at a time approach) in both DARWIN/PEPIN2 (INCERD module) and MENDEL.
-
Stochastic sampling and propagation in MENDEL (sampling can be done or by MENDEL either by an external sampler, scripts are given in order to use URANIE freeware [262]).
Uncertainty Quantification is the last step of the VVUQ process (Verification and Validation with Uncertainy Quantification) at the CEA. Its aim to give users a certain level of confidence in the numerical results, adding uncertainty bars and validating the fact that the observed discrepancies between numerical and experimental values are due to, respectively, nuclear data (and if possible which one), computer code accuracy and options, physical modeling (such as approximation on a geometry or a history of power), etc.
For the CEA computer codes, two approaches have been implemented. In DARWIN/PEPIN2, a first-order direct perturbation method (one at a time) approach has been introduced with the INCERD module. This approach consists of modifying one after the other all the parameters X (i.e. nuclear data) and to compute the Q.O.I. (Y) sensitivity to each parameter. In the second step, the variance of Y is computed through the classical sandwich formula:
Input uncertain parameters can be radioactive decay constants, radioactive decay energies, radioactive decay branching ratios, independent fission yields, multigroup microscopic cross sections, neutron-induced reaction branching ratios, α-particle or γ-ray intensities. Correlations can be taken into consideration, in particular for fission yields, branching ratios, or cross sections. Q.O.I. can be nuclide densities or activities, total activity, total decay heat, α-particle or γ-ray decay spectra.
In MENDEL, the first-order direct perturbation has been implemented for the same input parameters and Q.O.I. Furthermore, a stochastic approach based on random correlated sampling is also available. Sampling can be done either directly in MENDEL (from MENDEL v3.0, non-stratified sampling only for the moment), or using an external sampler like URANIE [263] (scripts provided with MENDEL are using LHS approach). Comparisons [94, 264] between the two approaches and different codes have shown a global equivalence of both methods, and discrepancies can be explained.
The nuclear data provided for the two main CEA’s evolution code systems, DARWIN/PEPIN2 and MENDEL, come from many international libraries as JEF-2, JEFF-3.1.1, JEFF-3.2, JENDL-4.0, JENDL-2015, ENDF/B-VII.1, ENDF/B-VIII.0, EAF-2003 and EAF-2010. The processing of these data is carried out by CEA’s main verification and processing system GALILÉE (release 0.3). The libraries for DARWIN/PEPIN2 and MENDEL, issued from the data processing by GALILÉE, consist of two main nuclear data types: the multigroup cross section (GENDF format) and the radioactive decay data.
The uncertainty data of many physical quantities are also included in these libraries. These data are used to calculate the uncertainty of decay heat, nuclide concentration, and radiation spectra (α-particle, γ-ray, and neutron) by DARWIN/PEPIN2 and MENDEL. The correlation between some physical quantities like independent fission yields, radioactive decay branching ratios, and neutron cross-sections, is taken into account in the uncertainty calculation. In the case of the neutron cross section, the covariance matrices come from COMAC (the nuclear database COvariance MAtrices from Cadarache).
7.2. SCALE
The SCALE modeling and simulation suite [182] for nuclear safety analysis and design, which is developed and maintained by Oak Ridge National Laboratory (ORNL), includes several depletion capabilities that enable calculation of decay heat in spent nuclear fuel for LWR or other reactor configurations. The ORIGEN point depletion and decay code, used worldwide for a variety of applications that require the calculation of nuclide inventories, decay heat, or neutron and gamma radiation emission rate and energy spectra, is the foundation of all depletion capabilities in SCALE. Since its first version [265] was deployed in 1973, ORIGEN [266] has evolved over the years, with continued modernization of the code, underlying methods, and associated nuclear data. ORIGEN includes two solvers for the depletion and decay equations: a hybrid matrix exponential/linear chains method (MATREX) and a Chebyshev Rational Approximation Method (CRAM). Under the TRITON [267] and Polaris [268] depletion sequences, ORIGEN serves as a depletion and decay solver, being coupled with a 1D, 2D, or 3D neutron transport solver to enable depletion and decay simulations for a variety of configurations. As a standalone code, ORIGEN has additional capabilities: (a) simulate continuous nuclide feed and chemical removal, which can be used to model reprocessing or liquid fuel systems and (b) generate alpha-particle, beta-electron, neutron, and gamma-ray emission spectra. ORIGEN is also the engine under the ORIGAMI (ORIGEN Assembly Isotopics) tool for performing rapid depletion and decay calculations to determine source terms for an LWR UO2 fuel assembly, in a 0D, 1D, 2D, or 3D modeling approximation of the fuel assembly.
ORIGEN tracks 174 actinides, 1149 fission products, and 974 activation products. It explicitly models all available nuclides and transitions in the current nuclear data for decay and neutron-induced transmutation in ENDF/B-VII.1. Cross-section data not available in ENDF/B-VII.1 are obtained from the JEFF-3.0/A special purpose European activation library. Nuclear decay data, fission product yields, and gamma-ray emission data are based on ENDF/B-VII.1 evaluations. The SCALE cross-section libraries that are available for the neutron transport solvers under Polaris or TRITON, in multigroup (MG) or continuous energy (CE), are based on ENDF/B-VII.1 or -VIII.0 evaluated data. Pre-generated, burnup-dependent ORIGEN reactor libraries based on ENDF/B-VII.1 are available in SCALE for a variety of reactor types and assembly designs; for LWR assembly configurations, these libraries cover initial enrichments up to 8.5% and burnups up to 82.5 GWd/t.
A rapid approach for determining an LWR assembly decay heat with SCALE is illustrated in Figure 35.
 |
Fig. 35. Decay heat simulation methodology with SCALE [269]. Left: generation of ORIGEN reactor library. Right: ORIGEN depletion and decay simulation. |
It includes two main computational steps: (1) generation of burnup-dependent ORIGEN reactor libraries for an LWR assembly of interest, using the TRITON or Polaris depletion sequence and (2) depletion and decay simulation with ORIGEN under the ORIGAMI tool. An alternate approach may consist of standalone ORIGEN decay-only simulations to a cooling time of interest, using as input the nuclide inventory binary file generated as a by-product by either TRITON or Polaris. An advantage of using ORIGAMI from an end-user perspective is the easiness of use and the ability to determine in seconds or minutes the assembly-average decay heat or the decay heat variation across the axial dimension of the fuel assembly. However, depending on the heterogeneity of the modeled configuration and the desired level of detail for the decay heat calculation, or the need for additional information, an end-user can take advantage of the flexibility of the depletion sequences or other tools in SCALE. For example, decay heat uncertainty analysis can be performed by using a model developed for the TRITON or Polaris depletion sequence within the Sampler uncertainty quantification in SCALE. That allows assessing the impact on the calculated decay heat of uncertainty in nuclear data (cross sections, fission yields, decay data) or input model parameters (e.g., initial enrichment, temperatures, geometry data).
7.3. SNF
Overview
Studsvik’s approach to spent nuclear fuel analysis combines nuclide concentrations, neutron fluxes, and cross sections, calculated by the neutron transport and depletion code CASMO5 [270], with irradiation history data from the reactor core simulator SIMULATE5 [271] and tabulated radionuclide decay data. These data sources are used and processed by the SNF code [272, 273] to compute the basic spent nuclear fuel characteristics: nuclide concentrations; radioactivity; decay heat power; photon sources and spectra; neutron source and spectra from spontaneous fission; neutron source and spectra from (α,n) reactions.
This code system is fully integrated with Studsvik’s Core Monitoring System (CMS5) and implicitly employs the three-dimensional (3D) discretization of the assemblies in the reactor core. Designed and implemented as a production tool, it provides comprehensive results per axial node of a fuel assembly or a fuel pin. In addition to the basic spent fuel characteristics, the SNF code is supplied with various optional modules intended to support and facilitate data preparation for analyses related to handling, transportation, and storage of spent fuel, including accident analyses, burnup credit in criticality safety evaluations, and dry cask loading scenarios. The decay heat power, computed by the summation method, is complemented by three standards for decay heat power in light water reactors: ANSI/ANS-5.1-2014 [136], DIN-25463-1/2-2014 [22, 25], and US NRC RG 3.54 Rev.2 |citeguide354 implemented as integrated methodology or as stand-alone applications.
The latest set of decay data implemented in the SNF code is based on ENDF/B-VII.1 [274]. With the release of ENDF/B-VIII.0 [211] and following its implementation [275] in CASMO5, a decay data set based on ENDF/B-VIII.0 was generated and available with the SNF code.
Methodology
The cross-section library, generated by the lattice physics code CASMO5, provides nuclide concentrations tabulated by exposure, moderator density history, control rod history, fuel temperature, and boron history. The nodewise exposure and accumulated history parameters, obtained from qualified operational reactor data or code simulation (SIMULATE5), are used as entry points in the interpolation routines and, with the power history model, are used to compute the end-of-life (EOL) nuclide concentration. The fuel assembly is divided into axial nodes (index: K) that may be further divided into sub-nodes (N). A sub-node is characterized by its associated lattice type (L). The concentration Cbase of a given nuclide (J) in sub-node (N) of node (K) is calculated as:
where
-
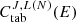 is the concentration (g/t) of nuclide J in lattice type L(N) at exposure E;
is the concentration (g/t) of nuclide J in lattice type L(N) at exposure E; -
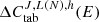 is the history-differential (difference between base and alternate depletion histories) concentration of nuclide J in lattice type L(N) at exposure E;
is the history-differential (difference between base and alternate depletion histories) concentration of nuclide J in lattice type L(N) at exposure E; -
ΔHh is a nodal history effect (moderator density, control, boron, void, fuel temperature, etc.).
In this equation, all concentrations are obtained by interpolation in two-dimensional tables for lattice type L to the nodal exposure E. The nodal concentrations, 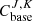 , are obtained by a weighted average over the sub-nodes in each node. Further, the individual nuclide concentrations are affected by the nodal power variations, the effect of which can be significant for many nuclides. The SNF code makes use of the nodal power histories (from the 3D core simulator) to apply “power history correction factors”,
, are obtained by a weighted average over the sub-nodes in each node. Further, the individual nuclide concentrations are affected by the nodal power variations, the effect of which can be significant for many nuclides. The SNF code makes use of the nodal power histories (from the 3D core simulator) to apply “power history correction factors”,  :
:
to the nodal concentrations. The power history correction factor for nuclide J in node K with burnup E is defined as the ratio of the final concentration, CJ, computed with the actual power history, to the reference concentration, Ctref, computed with the reference power level at the same burnup.
The EOL nuclide concentrations are then applied to the decay chains resolved by the Bateman system. The Bateman system is solved analytically by a method from reference [276] to obtain the final concentration, CtJ, K, at decay time t. The decay chains are built exactly as defined by the parent-daughter information from ENDF/B, which allows all other parameters (such as recoverable energies, decay constants, and emission spectra) to be applied implicitly. With the final nuclide concentrations, it is straightforward to compute the disintegration rates at cooling time t, and the recoverable energy is computed by:
where
-
RJ, K(t) is the disintegration rate of nuclide J in node K, after time t;
-
QmJ, K is the average recoverable energy per disintegration for particle type m.
Decay data
The SNF library includes basic data, such as decay constants, atomic masses, and nuclide transmutation chains; radiation emission spectra for photons from radioactive decay, (α,n) reactions, bremsstrahlung, and spontaneous fission; electrons and alpha particles from radioactive decay; neutrons from radioactive decay, spontaneous fission, and (α,n) reactions; decay heat production; and electro-atomic interaction data for bremsstrahlung production. These data are compiled from fundamental (ENDF/B, ENSDF [277], TENDL [278, 279]) and processed (ESTAR and ASTAR [280]) sources. For consistency with CASMO5, ENDF/B-VII.1 data are complemented with data from TENDL-2012 [281], and the ENDF/B-VIII.0 data are complemented with data from TENDL-2017 [282]. The evaluation and validation procedure of the decay data implemented in the SNF library is reported in reference [281].
The basic decay data set per nuclide (half-life, atomic mass, decay modes, and branching ratios, Q-values, and daughter isotopes) is entirely derived from ENDF/B, as are the discrete emission spectra for α, β, and x-rays. The uncertainty of line energies for the discrete spectra is provided by ENDF/B. When populating the photons in the user-defined energy groups, the intensity of a given line may be split equally between the adjacent groups if the group boundary falls within the corresponding line-uncertainty. For the continuum spectra for prompt photons emitted during spontaneous fission and α-decay, empirical correlations from reference [282] are adopted.
The (α,n) and (α,γ) reaction data are processed from TENDL by NJOY-2012 [283], with the alpha particle stopping powers for the elements, including compounds and mixtures, derived from ASTAR. The TENDL data for the oxygen isotopes 17O and 18O is complemented by (α,n) cross sections from Perry and Wilson [284]. The approach used for these isotopes was to rescale the neutron resonance data of Perry and Wilson to match the TENDL data at the upper energy of the resonance range (5.404 MeV for 17O and 5.18 MeV for 18O); the rescaling increased the cross sections below these energies by ≃25% and ≃4%, respectively. This allowed the cross-section representation to be extended to the upper limit of the SNF α-decay data (≃12 MeV). The photon production data were not rescaled. Compared to TENDL-2012, the TENDL-2017 based (α,n)-yields are on average about 2% smaller.
The continuum spectra for electrons and positrons were calculated by the method of Stamatelatos and England [285], coupled with the Fermi function approximation of Schenter and Vogel [286], with the spectrum endpoint energies provided in the ENDF/B decay sub-library. The external bremsstrahlung cross sections and production kernels were processed from the ENDF/B electron sub-library, while the electron-stopping power data were calculated with the ESTAR application.
7.4. FISPIN
FISPIN is a spent fuel inventory code developed in the UK. Initially developed by UKAEA [287], in the 1970s but subsequently developed by the National Nuclear Laboratory, it simulates the production and destruction of three groups of nuclides; heavy elements (associated with the production and decay chains from natural thorium and uranium isotopes), fission products and products of activation of naturally occurring elements irradiated in reactors. The solution method is developed from the EXTRA code developed by Sidell [288]. The code uses burnup-dependent cross sections, fission product yields, energy per fission, atomic masses, isotopic abundances, and decay data to solve the production and destruction equations for each nuclide to determine the changes in the composition during irradiation. The code can use steps of irradiation or cooling defined by neutron flux in n/cm2/s and irradiation duration, the rating in MW/t and time to reach required irradiation in MWd/t (aka burnup), a set of fission rates and time, or for no neutron flux/cooling times a duration or cooling time. Additionally, at any step in the irradiation or cooling, the elements can be separated either by removing all but a set of specific elements of which a fraction passes into a product stream during chemical processing, or letting through all but a specific list of elements for which only a fraction is passed through to simulate a waste stream. Various output options exist to list at each step the masses, activities, decay heat, gamma-ray emissions, β activities and energy released, α activities and energy released, and neutron emission from both spontaneous fission and (α,n) reactions for an arbitrarily defined compound. The output can be split by nuclide or element to support chemical engineering applications. FISPIN10A is the latest version of the code and is released with a GUI under Windows or Linux that simplifies production of FISPIN runs. It includes a set of burnup-dependent neutron cross-section libraries for Magnox, AGR, PWR, and BWR fuels with natural enrichment for Magnox, up to 4% enrichment for AGR, and up to 5% for PWR and BWR. The validation for this code is available from reference [289]. FISPIN11 is a new version of the code currently being developed, but not yet released. It uses a purpose-developed Rosenbrock stiff problem integration method and is designed to be called an application via an API so that it can be incorporated into purpose-built wrappers around the FISPIN11 kernel. This simplifies QA of the code by only solving the production/destruction equations in FISPIN11, with data preparation and conversion of the output into user requirements being carried out with the developed wrappers.
7.5. EVOLCODE
The EVOLCODE 2.0 system is a burnup code developed and maintained at CIEMAT for more than 20 years. It combines neutron transport and depletion calculations to describe the burnup evolution of either critical reactors or subcritical systems operating in any neutron spectrum regime. The code has been focused on the estimation of a great variety of nuclear reactor parameters, with a particular interest in the nuclide composition evolution of the fuel in a nuclear reactor and also in the neutron transport characterization of the core [290].
The present version of the code allows using any published version of the general MC transport code MCNP/MCNPX (Pelowitz, 2014) for the neutron transport part of the calculation. This code is a Monte Carlo radiation-transport code able to track, among others, neutrons, photons, and electrons. Complex statistical processes can be modeled without explicitly solving the Boltzmann equations, by means of simulating individual neutrons and then analyzing statistical averages of their interactions with the material medium. The depletion part of EVOLCODE can be performed by one of two codes: the activation code ACAB [291] and the ORIGEN code [292]. Both codes solve the Bateman equation using the matrix exponential method.
The EVOLCODE 2.0 system can to work with any basic database, with the only limitation that the cross sections are formatted in ACE format [293], usable by MCNP, to ensure coherence. Among the data that the code uses from the library, some can be highlighted, such as the cross sections, decay data (including the heat emission per decay), fission product yields, reaction branching ratios, and the probability tables to treat unresolved-resonance self-shielding as MCNP does. The nuclear data library most commonly used in EVOLCODE is the JEFF-3.3 nuclear data library [58].
7.6. VESTA
VESTA [294] is a Monte Carlo depletion code developed by IRSN, which couples a continuous energy Monte Carlo neutron transport code with a depletion module. VESTA validation calculations were performed using the JEFF-3.1, JEFF-3.2, ENDF/B-VII.0, and ENDF/B-VII.1 nuclear data libraries. VESTA 2.1.5 calculations were performed using MCNPX 2.6.0 and PHOENIX codes, with the JEFF-3.1 and ENDF/B-VII.0 nuclear data libraries. VESTA 2.2 calculations were performed using MCNP6.1 and PHOENIX codes, with the JEFF-3.2 and ENDF/B-VII.1 nuclear data libraries.
These libraries include the required cross-section data for the transport and reaction rate calculation but also the neutron induced fission yield data, isomeric branching ratio data, and decay data. The ORIGEN 2.2 library used as the base library is PWRU50.LIB. This base library is used only as a source for cross-section and isomeric branching ratio data when the information is missing in the nuclear data library.
No time-dependent temperature evolution has been modeled and an average boron concentration during irradiation is considered. The irradiation history is subdivided into depletion steps of 1 GWd/tHM, according to the VESTA validation procedure (see Ref. [295]). The number of particles per cycle and the number of active cycles for the MCNP calculation are determined to ensure statistical errors in the neutron flux of less than 0.1%.
7.7. Serpent
Serpent is a multi-purpose three-dimensional continuous-energy Monte Carlo particle transport code [296]. Serpent has been developed at VTT Finland since 2004. The original motivation for Serpent development was to provide spatial homogenization based on the high-accuracy Monte Carlo method [297]. However, since the early years, Serpent’s applications have been greatly expanded from reactor physics to fusion applications, photon transport, and multi-physics modeling. Currently, Serpent development is carried out in the context of the development of a new computational framework for coupled core physics calculations, Kraken [298].
The geometry routine in Serpent is based on a three-dimensional constructive solid geometry (CSG) model. The available selection of elementary quadratic and derived surface types enables the modeling of a large scale of different geometries and reactor types. CAD-based geometry type is also available for the modeling of complicated and irregular systems [299]. Particle tracking in Serpent is handled through a combination of conventional ray-tracing-based surface tracking and the rejection sampling-based delta-tracking method. Surface tracking is used in the presence of heavy absorbers when the efficiency of delta-tracking rejection sampling becomes low.
Serpent includes a built-in burnup calculation routine utilizing the CRAM method (Chebyshev Rational Approximation) to solve the Bateman depletion equations [300]. In a typical burnup calculation, a total number of 1200–1600 nuclide concentrations are tracked including 250–300 actinides and fission products with cross sections. The output includes depletion zone-wise, material-wise, and total nuclide concentrations, masses, activities, decay heat, and other parameters. The decay heat of a given material is based on nuclide concentrations, decay constants, and total energy emitted in a decay. The latter two components are read in Serpent from ACE format nuclear data libraries. Currently at VTT, nuclear data based on JEFF-3.2, JEFF-3.1.1, ENDF/B-VII.1, and JENDL-4.0 are available.
Serpent is available for academic users through the OECD/NEA databank and Radiation Safety Information Computational Center (RSICC). Commercial licenses are issued by VTT.
7.8. Codes and libraries developed by JAEA
Japan Atomic Energy Agency (JAEA) has developed some depletion calculation codes, among which two major codes: MVP-BURN [301] and SWAT4 [302] are briefly introduced in the following.
MVP-BURN is a depletion calculation code based on Bateman’s method coupled with the continuous-energy Monte Carlo code MVP [303] for neutron flux and effective cross section calculation. MVP-BURN is now available as a part of the MVP3 package, which is the latest version of MVP. As latest nuclear data libraries, cross-section data libraries based on JENDL-4.0, ENDF/B-VII.1 and JEFF-3.2, and a burnup chain data library based on JENDL-4.0 are available. Recently, MVP-BURN (MVP3) was used in the blind benchmark exercise for spent nuclear fuel decay heat and its performance was compared [15].
 |
Fig. 36. Radioactivity (left) and photon intensity (right) from debris of Fukushima-Daiichi nuclear power plant estimated from the decay data of JENDL-5, JENDL/DDF-2015, JEFF-3.3, and ENDF/B-VIII.0 (data are provided by courtesy of T. Matsumura (CLADS, JAEA)) |
SWAT4 is a depletion calculation code system driving ORIGEN2 [292] for depletion calculation and three neutron transportation calculation codes: the deterministic code SRAC [304], and the continuous energy Monte Carlo codes MVP and MCNP. Users select a neutron transportation solver from these three codes depending on their purpose. SWAT4 works as an interface between ORIGEN2 and the selected neutron transportation solver, and various calculation capabilities of ORIGEN2 are available. Cross-section data of SWAT4 depends on a cross-section library of the selected neutron transportation code. Other nuclear data such as radioactive decay and fission yield data is applied from basic ORIGEN2 libraries or other libraries for ORIGEN2 such as ORLIBJ40 [305], which is a nuclear data library set based on JENDL-4.0 for ORIGEN2.
Regarding nuclear data libraries, JENDL-5, the latest version of the JENDL series, provides comprehensive evaluated data of nuclear reactions and decays, thermal neutron scattering kernel, fission product yields, etc. to facilitate nuclear science and technology covering a variety of applications not only for nuclear energy but also for radiation-related fields. The number of nuclides of neutron reaction data increased to 795 which is almost double of 406 of JENDL-4.0 to cover various applications. New evaluations were carried out for light nuclides, actinides, structure materials, fission products, minor-actinides using up-to-date experimental data and theoretical tools.
Thermal scattering kernel of light water, heavy water, etc. were also newly evaluated. The benchmark tests mainly for light-water and fast-neutron reactors and neutron shielding were carried out, showing globally a better performance to JENDL-4.0. New evaluations were also carried out for fission product yield and decay data, which are of particular importance for decay heat estimations.
The characteristic point of the evaluation of JENDL-5 fission product yields is the introduction of theoretically calculated nuclear shell corrections in the independent fission product yields and of the Hauser-Feshbach statistical model in calculating the fraction of isomer states [306]. The evaluated data of decay data is mainly based on ENSDF. In addition, newly evaluated data of delayed neutron emission and spectra were added, based on studies from the IAEA CRP [307], and theoretically calculated particle emission spectra.
The JENDL-5 fission product yield and decay data are benchmarked by using PIE data of Mihama-3 and Takahama-3, decay heat data of instant neutron irradiation carried out at the Oak Ridge National Laboratory, Yayoi fast reactor facility (University of Tokyo), delayed neutron yield data, and anti-neutrino spectra data [212, 306].
Good improvement for delayed neutron yield evaluations was therefore obtained [212]. Verifications by comparing the calculated radioactivity and photon intensity from the debris of the Fukushima-Daiichi nuclear power plant were carried out, including calculations with the ENDF-B/VIII.0 and JEFF-3.3 libraries. One of the typical results is shown in Figure 36, where the fuel compositions are taken from reference [308]. It can be seen that both radioactivity and photon intensity of JENDL/DDF-2015 show smaller values than other libraries. This is due to the lack of several nuclear data, which are the isomer state of 235U, x-rays of 137mBa, γ-rays of 241Am, etc. Those issues are fixed for JENDL-5 and results are much closer to ENDF-B/VIII.0 and JEFF-3.3.
7.9. COMPASS
COMPASS is a burnup analysis code system developed by CRIEPI for the prediction of neutron transport and nuclide composition in large-scale geometry such as multi-assembly or whole core geometry [309–312]. COMPASS uses a general-purpose continuous energy Monte Carlo code MVP3 [303] as neutron transport calculation solver, the CRAM method [300] and burnup chain-data based on JENDL-4.0 (ChainJ40) [313] in the depletion solver for nuclide composition calculation. All nuclear data libraries such as JENDL-4.0, ENDF/B-VII.1, and JEFF-3.2 bundled in MVP3 are available in COMPASS. A function of unified geometry treatment is implemented in COMPASS for coupled calculations with thermal-hydraulic and fuel performance calculation codes. One of the advantages of COMPASS is flexibility in setting calculation conditions and parameters. For example, COMPASS can change material temperature and geometry parameters in each calculation step and use all options of MVP3 code (e.g. exact resonance elastic scattering model [314]). The depletion solver in COMPASS has been validated enough by Post Irradiation Examination (PIE) analysis for PWR and BWR 55 assemblies.
7.10. ACAB
The ACAB code is a computer program designed to perform activation and transmutation calculations for nuclear applications [224]. ACAB considers decay transitions that proceed from the ground, first, and second isomeric states. All the nuclear reaction processes and all the corresponding reaction products are treated in ACAB code.
ACAB’s primary result is nuclide concentrations as a function of time for each spatial interval or zone defined in the system. From the nuclide concentrations, ACAB is able to generate radionuclide activities, decay heat (total and contributions from the different types of radiation), decay gamma spectra, contact dose rates, waste disposal ratings, offsite doses to the most exposed individual, as well as collective doses and associated consequences, radiotoxicity (committed effective dose equivalent by inhalation and ingestion) and neutron emission among other quantities that depend upon nuclide concentrations.
In addition to the calculational facilities, ACAB also performs sensitivity analysis of the activation results. Critical radionuclides are identified and pathways contributing to their production are evaluated. ACAB is able to compute uncertainties both on inventory calculations and inventory-related quantities. The method is based on the application of the Monte Carlo technique, it allows dealing efficiently with the synergic/global effect of the uncertainties of the total set of cross sections to obtain the overall uncertainty on the radiological calculations.
The potential of ACAB for fission reactor applications has been proven to be reliable in computing accurate nuclide inventory. Examples of results using ACAB coupled to a Monte Carlo neutron transport code are: a simple UO2 pin-cell benchmark [315], an ATRIUM-10XP design BWR fuel assembly [316], a high temperature gas-cooled reactor plutonium burnup benchmark [317]. In addition, ACAB is able to predict decay heat and delayed neutron emission rate, average neutron energy and neutron delayed spectra after a neutron fission pulse [318].
8. Validation
Validation is an essential step to gain confidence in simulation results. It is the link between experiment and calculation. The latter uses the former to derive prediction power, biases, and uncertainties. The former is adapted based on the needs of the latter. Decay heat validation is a field that cannot be extensively be described in this report, given the large amount of related publications; only an overview, with some relevant references is provided in the following.
Not all codes and nuclear data are included, and the focus is here on decay heat. It is rather common that the same codes are also validated for other quantities, such as keff, nuclide concentrations, or radiation emissions (gamma, beta, alpha, neutron) in SNF. Such validation will be partially referred to.
8.1. Definitions
A number of terms are often used together, such as verification, quality assurance, validation, and uncertainty quantification. The definition of these processes can vary from one organization to the other, but global notions are generally common. Detailed examples can be found in references [319–321].
Verification consists in the actions that demonstrate that a specific code (or its parts) is performing as expected, given the initial requirements from the design phase. It can for instance be a well-defined formalized process having the goal of determining if specific equations are correctly solved from the numerical and software aspects.
Quality Assurance (QA) refers to the process of determining and documenting whether or not items, processes, or documents which support the computer code conform to specified requirements [322].
Validation refers to the process of evaluating a computer code after the completion of its development and prior to its application, to ensure compliance with the requirements of the intended application. Validation provides the evidence that the computer code is fit for the intended purpose, by comparison of the computed results with data from experiments or other trusted sources [322].
Quite often, verification and validation of a computational tool go hand in hand and are referred to as V and V. Herein validation, the focus of this section, refers to the comparison of computed results with data from experiments. Uncertainty quantification, which is an important part of the validation process, is discussed in Sections 9 and 6.6.
An important aspect of the decay heat validation is assessing the effect of nuclear data used with a computational tool on the comparison calculation experiment. For the same computational tool, results obtained with different sets of nuclear data (cross sections, fission yield, decay data), could be significantly different. When comparing the performance of various computational tools in predicting decay heat, it is recommended for completeness to cite both the computational tool and associated nuclear data used for the simulation, rather than the name of the computational tool only.
8.2. Validation based on direct decay heat measurements
The measurement data serving as the basis of the validation studies summarized here were obtained from decay heat integral experiments (full assembly or fuel rods within an assembly), or from pulse fission experiments for fissile materials (foils). Full-assembly decay heat experiments are generally feasible and performed for cooling times greater than 2–3 years; these cooling times are of particular importance to spent nuclear fuel storage, transportation, and disposal applications. Full-assembly decay heat experiments are not feasible for cooling times up to 105 s that are of interest for evaluation of postulated loss-of-coolant accident scenarios; for this time range, pulse fission experiments serve for determining the energy released following reactor shutdown to derive decay heat. These experiments generally involve gamma and beta spectroscopy measurements to derive decay heat from the individual gamma and beta energy components.
8.2.1. Decay heat validation of ALEPH2
ALEPH2 has been extensively validated based on various sets of experimental data relevant to spent nuclear fuel applications, including for nuclide inventories [323–325] and decay heat. For LWR spent nuclear fuel, ALEPH2 was validated using based on full-assembly decay heat measurements performed at the Clab facility for 25 PWR and 34 BWR spent fuel assemblies. Simulation results obtained by running ALEPH2 with various neutron transport and fission yields showed the calculated decay heat values underestimate the measurement data by less than 4% for PWR assemblies and less than 6% for BWR assemblies [326].
It is also worth mentioning that additional validation of ALEPH2 for decay heat calculations for fast reactor spent nuclear fuel was performed, using limited information available from the JOYO MK-II core experimental program. The obtained results showed an underestimation of less than 7% [327].
8.2.2. Decay heat validation of VESTA 2.2
VESTA 2.2.0 has been extensively validated for decay heat calculations for intermediate and long cooling times applications, based on full-assembly decay heat measurements for 52 PWR UO2 assemblies. These 52 assembly measurements include: 34 measurements performed by the Clab program, 14 measurements from the General Electric program, and 4 measurements from the HEDL program.
Using the JEFF-3.1, JEFF-3.2, ENDF/B-VII.0 and ENDF/B-VII.1 nuclear data libraries, VESTA calculates the assembly decay heat for almost all cases within 4% of the measured decay heat.
On average, the calculated decay heat values that used JEFF-3.1 appear to result in a systematic underestimation of about 2%, while those that used ENDF/B-VII.0 led to a systematic underestimation of about 0.5% with almost all points within the two sigma experimental uncertainty. While the results for the comparison calculation-measurement for the GE experimental data are similar to those obtained for the Clab data, it appears that some specific measurements from the HEDL data are problematic; specifically, this concern an unrealistic large uncertainty on the final discharge burnup for two assemblies, which will require further investigation. When omitting these two assemblies from the HEDL data set, the average calculated-to-experimental decay heat for the aggregate set of the Clab, GE and HEDL measurements is 0.979 for JEFF-3.1 and 0.996 for ENDF/B-VII.0 calculations.
The validation calculations performed with the JEFF-3.2 and ENDF/B-VII.1 libraries considered only the Clab measurements. Using the JEFF-3.2 nuclear data library, except for a few outliers, VESTA calculates the assembly decay heat for almost all cases within 3% of the measured decay heat. On average, the JEFF-3.2 calculated decay heat values underestimate the measured data by about 2%. Using the ENDF/B-VII.1 nuclear data library, all VESTA results overestimate the measured data by about 0.5%, with almost all points being within the two sigma of the reported experimental uncertainty.
8.2.3. Validation of DARWIN/PEPIN2 and MENDEL
Validation tests should be the responsibility of another group of persons (i.e., not the developers). Generally, such tests are realized by the developers and integrated in the non-regression base. Nevertheless, the full validation of the code system needs a group of users able to use the code differently from what the developers were initially thinking of. They should have access to a large data bank of experimental data, and use it for the code validation. At the CEA, this work is mainly done by the group elaborating on the DARWIN2 package. Validation tests consist of PIE, activation experiments, decay heat measurements after fission pulse or irradiation, and the scope tends to be as complete as possible, to fully validate the model (computer code and nuclear data).
8.2.4. Decay heat validation of CASMO5 and SNF
The validation effort with the deterministic transport code CASMO5, regarding integral measurements of assembly decay heat, can be found in a number of publications, for instance, references [13, 14, 34]. In parallel, indirect validation was also performed using Post Irradiation Examination and measured nuclide concentrations, such as in references [33, 34, 234, 245, 246]. Different nuclear data libraries were used, indicating spread of data similar to other codes. In parallel, the impact of the nuclear data uncertainties was also calculated using the irradiation histories from either the Clab assemblies, or ARIANE PIE data (see mentioned references).
Regarding the SNF code, it calculates nuclide concentrations and decay heat (among other quantities) either based on irradiation histories specified by the user or based on core follow-up simulations from the SIMULATE-3 or SIMULATE5 codes. As for CASMO5, it was validated with PIE nuclide concentrations [245, 328, 329], and with Clab decay heat measurements (including different nuclear data libraries) [330].
8.2.5. Decay heat validation of SCALE
Validation of computational capabilities in the SCALE code system for decay heat prediction has been documented for various versions of SCALE, starting with 5.1 [266] and continuing with 6.1 [79], 6.2 [269, 337], and 6.3 [11]. This continuing validation effort has involved the use over the years of different ENDF nuclear data libraries, from ENDF/B-V through ENDF/B-VIII.0.
The most recent validation for decay heat at cooling times of relevance to transportation, storage, and disposal of spent nuclear fuel was performed based on 91 PWR and 145 BWR full-assembly decay heat measurements. These measurements cover a cooling time ranging from 2 to 27 years for PWRs and BWRs, a burnup range of 18-51 GWd/MTU for PWRs and a burnup range of 5-45 GWd/MTU for BWRs. The decay heat predicted with SCALE 6.2 and ENDF/B-VII.1 libraries is on average within 1% of the experiment results (σ = 1.6%) for PWRs, and within 2% of the experiment results σ = 7.7%) for BWRs, see reference [269]. The validation study also looked at the effect of using a different nuclear data library. The C/E results obtained with SCALE 6.2.4/ENDF/B-VII.1 and those obtained with SCALE 6.1/ENDF/B-VII.0 when using a same basis of 121 LWR assembly measurements differed on average by 0.6% (σ = 0.5%) for PWR assemblies and by 1.2% (σ = 0.8%) for BWR assemblies. This difference was found to be primarily due to the change in the 238Pu capture cross-section between ENDF/B-VII.0 and ENDF/B-VII.1 [269].
Validation of SCALE 6.2 with ENDF/B-VII.1 libraries for very short cooling times was based on data from pulse fission experiments designed to determine the energy release from fission of 233U, 235U, 238U, 239Pu, 241Pu, and 232Th. Overall, this validation basis covered cooling times from 0.2 s to 11 h following fission. The results obtained showed generally good agreement between calculated and measured values, within the level of the reported measurement uncertainties [269].
8.3. Indirect validation
As mentioned, a number of transport and depletion codes are also validated for nuclide concentrations, based on Post Irradiation Experiments as for instance described in the SFCOMPO database [32], or with criticality-safety benchmarks, as from the ICSBEP database. In the latter case, the fuel under consideration is fresh and does not directly overlap with the SNF characteristics. Such validation is nevertheless useful for decay heat as it demonstrates the code (and nuclear data) performances for neutron transport. In the case of PIE validation, the prediction of nuclide concentrations after irradiation and cooling periods defines the code predictions for calculating the fission product and actinide concentrations, which play a key role in the calculation of decay heat. In both cases, such indirect validation for decay heat is also of prime importance and demonstrates the complexity of a full validation scheme. A number of publications can be found for PIE validations, with codes also used in decay heat calculations, for instance in references [245, 328, 331].
Another source of indirect validation for SNF decay heat is the calculation of pulse irradiations and comparisons with measurements, as presented in Section 6.4.4. The gamma-ray and beta-electron emissions on different actinide targets were measured at short cooling time (down to 1 second), with well-characterized neutron beam, which represent the only available experimental data for a short time range. An example of such decay heat validation can be found in reference [186].
9. Recommendations
Based on the current understanding of the physical phenomena at stakes in the decay heat for current spent nuclear fuel assemblies, the following recommendations are proposed. This list is not comprehensive, yet represents the main priorities recognized at the time of this report.
9.1. Extending the current experimental database
As mentioned in Section 5, only one full assembly calorimeter is nowadays in activity worldwide. The Clab calorimeter is a unique facility, dedicated to measuring assembly decay heat coming from Swedish nuclear power plants. The high-quality published measurements, with the necessary information on the assemblies, allow for a number of code validations. Most of the measured values come from reference [76], complemented with information from ORNL reports. They correspond to assemblies irradiated up to the beginning of the year 2000, with initial enrichments and end-of-life burnup lower than today’s typical values. Additionally, these assemblies contained UO2 fuel solely.
A new experimental program is currently being analyzed with the support of SKB and EPRI, expanding the range of burnup and initial enrichment to higher values (possibly up to 55 MWd/kgHM burnup and 4.1% 235U enrichment). Such results, when available will help in covering part of the present gap with respect to the SNF characteristics as employed nowadays. Assemblies currently used in reactor cycles generally have higher initial enrichment (close or slightly higher than 5.0%) and are reaching average burnup values higher than 60 MWd/kgHM. The cooling times of interest, in the case of deep geological repository are also different than the ones measured (from 2 to 27 years), mainly due to the delays in the start of such facilities (as well as encapsulation facilities). Finally, the magnitude of the measured decay heat rate is relatively restricted: the Clab and GE-Morris measurements correspond to values between 20 and 940 W, with the addition of the recent measurements on five assemblies, from 660 to 1660 W [15]. Most of the measured values are in the range of 150 to 500 W, which is rather limited for a complete validation work.
There is therefore a clear need for additional integral measurements on SNF with higher burnup, higher initial enrichment, higher decay heat rate values, and different cooling times, ideally at different facilities. Another pressing need concerns MOX assemblies. There are currently no integral measurements in the public literature on MOX SNF. Such assemblies have been used in more than 40 reactors worldwide and a number of such SNFs are currently in storage. The lack of decay heat measurements for this type of assemblie is limiting the current validation capabilities. Finally, other types of SNF do not have measured decay heat: VVER and CANDU assemblies and more recently ATF assemblies.
In parallel to integral decay heat measurements, fission pulse decay measurements also bring valuable information, as presented in Section 6.4.4, helping to disentangle different components of the total decay heat, with direct information for the underlying nuclear data (fission yields and decay data). The compilations used for validations, mainly references [44, 107, 115, 125, 126] for thermal neutron-induced fission, are based on measurement methods and reported uncertainties which can also be nowadays improved. Better estimation of SNF decay heat will therefore benefit from new fission pulse decay measurements based on modern techniques.
9.2. Improving theoretical understanding and nuclear data
As presented in Section 6, various possibilities exist for the prediction of the SNF decay heat (e.g. simple formula, summation methods, standard methods). Some of them rely on a physical description of decay phenomena and therefore depend on the correct estimation (or simply the availability) of specific nuclear data (half-lives, decay energies, decay modes). In the case of heavy actinides produced from many subsequent neutron captures, such as curium isotopes, a number of fission and capture cross sections are also of importance. For fission products, both independent fission yields and capture cross-sections can affect nuclide concentrations and consequently the energy released during the sum of their decay. Improving the knowledge of such nuclear data will impact the prediction capabilities for nuclide concentrations and consequently for decay heat. It is therefore recommended to improve the quality of nuclear data for nuclides of importance for decay heat.
In parallel, the handling of such decay data can be mathematically challenging, for instance, due to the large difference in the order of magnitude of half-lives. Different numerical solvers are used such as the matrix exponential method [220], the Ordinary Differential Equations (ODE) [97], the CRAM matrix exponential method [296], or the transmutation trajectory analysis (TTA) [215]. The implementation of such methods (even for the same method) can lead to differences, affecting calculated quantities such as the decay heat. Benchmarking these methods and their implementations can help in improving the precision of calculations, effectively removing biases due to numerical methods.
Finally, physical phenomena might need to be better taken into account, such as delayed fission. After a fission event, a number of delayed neutrons are emitted, up to minutes following the prompt release of energy (for instance from the decay of 87Br). Such neutrons can also generate fission events. It was shown in Section 6.2 that these delayed fission events can be of significant fraction of the total decay heat up to one or two minutes after a reactor shutdown. The question of how well is this process taken into account by simulation codes is of relevance for short-term cooling after a reactor transient, as neglecting it would seriously undermine the estimation of the core decay heat.
9.3. Best estimate calculations and conservative estimations
As mentioned in Section 6, the prediction of decay heat can be achieved with detailed calculations based on summation methods, but also with standard methods such as ISO, ANSI, or DIN [22, 26, 27]. Such standard methods have the advantage to provide fast answers, with a certain amount of conservatism. Still, some of them require fission fractions as a function of irradiation history (for the main four actinides contributing to fission events), and these quantities are often derived from dedicated transport calculations. It is recommended to use more precise methods for final assessments, performing dedicated transport and depletion calculations based on specified irradiation history and assembly characteristics. If an amount of conservatism is still required, it is preferable to explicitly add it as a separate quantity.
9.4. Biases and uncertainties
Biases and uncertainties are as important to estimate as the decay heat values themselves. They depend on the input data and assumptions, as well as on model simplifications and calculation methods. Needless to say biases also depend on the reference data, their uncertainties, and correlations. As many possibilities can be selected, it is of prime importance to indicate the maximum amount of information regarding the performed calculations: code versions, nuclear data libraries, calculation methods and experimental database.
Regarding calculated uncertainties, users are generally facing many choices for the assumptions regarding input values, such as the recommendations provided in reference [232], various uncertainties found in the open literature or in-house values. There are for instance currently no recommendations on fission yield correlations, or decay data correlations, which directly impact calculated uncertainties on decay heat. It is not uncommon to find differences larger than factor 2 or 3 for the uncertainties on the same calculated quantities, such as nuclide concentrations. Similarly, operational and technological parameters are not systematically recorded with recommended uncertainties (and probability density functions).
It is therefore of important to provide the user community with systematic recommendations for uncertainties, correlations and probability density functions for all parameters and physical quantities used in simulations. Additional recommendations shall cover sampling and uncertainty propagation methods.
9.5. Other recommendations
The list of recommendations can be extended to many other features, most not only applicable to decay heat calculations but solely linked to simulation methods. Such aspects include but are not limited to:
-
Redundancy. During the characterization of the SNF for various practical applications (safeguard, storage, handling, final disposal), redundancy of calculations, measurements, or verification of any nature is a best practice in order to identify potential errors or mistakes, for instance from human nature. In the example of selecting SNFs for canister loading, a redundancy can consist of comparing the declared SNF burnup (from plant data) with gamma-ray or neutron emission measurements at the time of loading. Unexpected differences may indicate potential mishandling at a given stage of identification. In the case of decay heat calculation, predictions by independent parties can help identify various types of mistakes.
-
Comparison of code implementation. It is known that different coding implementations of the same mathematical model can lead to differences, sometimes beyond numerical precision. Comparing modules of codes, which are expected to perform similar tasks, can be useful to improve speed and efficiency, and detect potential errors.
-
Blind benchmarks. The term of “blind benchmark” is understood here as the exercise of performing similar simulations between different (independent) partners, without accessing any information concerning the calculations of other participants, or measurements to be later compared to, for the full duration of the project. The main advantage of this approach is to avoid having interference effects between participants themselves and between simulations and measurements. The consequence is a true independence of calculations, performed with a common set of information. If such strict conditions are accepted, different iterations are possible, while keeping track of changes: a second step can be performed after a limited comparison between calculated quantities, or with measurements. The evolution of calculated values as a function of iteration can be an indication of improved knowledge, which can be clearly quantified. The consequences can be interpreted as simulating the realistic situation where no experimental will be available, and other calculations to be compared to. It is therefore recommended to perform new benchmarks as blind, helping to better assess results obtained in realistic assignments.
-
User effect. The user effect can lead to non-negligible variations of calculated or measured quantities. It can happen due to different interpretations of the same information, ambiguity of definitions, selections of different methodological options (not described in a task definition), or simple mistakes. It is often difficult to quantify, in part due to the absence of blind benchmarks, or to the absence of redundancy. It was nevertheless observed in different situations and it is necessary to include a measure of this effect in dedicated best estimate calculations, with uncertainties. Missing to recognize it would lead to an underestimation of the total uncertainty.
Some of these four items are often partially addressed within institutes, using verification procedures, so-called logbooks, archiving of data, often regulated by ISO or national standards. The validation of the adequacy of these steps can nevertheless be tested within the international community.
10. Conclusion
The activities performed in this subgroup 12 (SG12), started in 2022 under the auspices of the NEA’s WPNCS, aimed at describing the current knowledge on decay heat (or thermal decay power) for existing SNF assemblies. A number of different areas were reviewed: theoretical description, simulation, standard methods, and measurements. One of the motivations for this work is the current needs of the nuclear industry for the estimation of decay heat during short-term cooling (such as in core transient) and in the back-end of the fuel cycle (SNF wet and dry storage, up to and including final repository).
As highlighted in this report, the evolution of fuel characteristics for current LWR over the past decades is following a trend of higher initial enrichment, higher average assembly burnup, and extended storage. It is foreseen that in the future, the initial fuel enrichment will commonly go beyond 5% in 235U, also leading to higher average burnup values. The need for code and method validation (as well as for nuclear data libraries) is as acute as in the past, and the current experimental databases, used for validation, are not covering all SNF characteristics (neither fuel type, e.g. MOX, CANDU or VVER fuel, or ATF fuel). It was therefore recognized in this report that validation efforts need to continue, with a number of consequences in the areas mentioned above.
Experimentally, it was acknowledged that the existing set of decay heat measurements is highly valuable yet limited, as only one calorimeter is today in use (at SKB, Sweden). Such limited availability has two main consequences: (1) all recent (and eventually new) measurements come from a unique facility, rendering redundancy and independent checking impossible, and (2) all recent (and eventually new) measurements are performed on a limited set of SNF, corresponding to the assemblies in use in Sweden.
From the simulation aspect, new needs related to existing SNF assemblies mainly arise from stringent economic requirements and ever stricter safety rules related to core transient, extended storage, and deep geological repositories. Calculations of SNF decay heat need to be accurately described in terms of biases, outliers, confidence intervals, or uncertainties. When possible, direct validation (mostly for cooling time less than a few decades) is still necessary, but for time periods of interest for deep geological repositories, other questions may come to light. Generally, it was acknowledged that inputs used in simulations (e.g. fuel and moderator temperatures, void, irradiation history) can also be uncertain, leading to uncertainties in calculated decay heat values. New needs for the understanding of important parameters were also recognized, such as assembly average or local burnup, and the impact of the knowledge of detailed irradiation history. Consequently, the improvements in calculated decay heat values pushed for a better knowledge of experimental methods and uncertainties, a better assessment of key parameters for simulations, and also for making use of various sources of information not directly linked to decay heat, such as Post Irradiation Experiments and full core simulations.
As mentioned, the SG12 brought to light a number of areas where additional efforts will be beneficiary and recommendations are provided in Section 9. As decay heat is one of many characteristics of SNF assemblies, the SG12 activities were also closely connected with the needs in criticality-safety studies, as well as for safeguard requirements. Other international activities were progressing in parallel with common subjects of interest, such as the European Joint Programme on Radioactive Waste Management (EURAD), and the International Atomic Energy Agency Coordinated Research Project on Spent Fuel Characterization (T13018). In the United States, it was also recognized that the existing experimental database needed to grow, and at the time of this subgroup, a report from EPRI regarding new experimental campaigns using the SKB calorimeter was being finalized. The latter will provide new measured decay heat values for SNF assemblies generally having different cooling times, higher burnup, and initial enrichment compared to the currently available set. Finally, during the course of the SG12, two projects for new calorimeters were presented, one in Switzerland at the Gösgen power plant, and one in France, developed by the CEA and EDF. If realized, such projects will address many of the existing issues, regarding the need for measurements on MOX fuel, on a variety of different assembly designs, and on redundancy.
The largest success of this work was to bring together actors from the nuclear industry, research, and safety organizations, having possibly contrasting horizons, requirements and needs. Experiences were shared in constructive ways and a consensus was found to deliver a significant message: better estimations of decay heat are needed.
For uranium fuel with high 235U enrichment, the actinide’s short-term contribution to decay heat power comes from the transmutation products of 235U, i.e. 237U and 238Np [46].
Acknowledgments
The authors and contributors of this work are very grateful for the support of the NEA WPNCS.
Funding
This research did not receive any specific funding.
Conflicts of interest
The authors declare that they have no competing interests to report.
Data availability statement
This article has no associated data generated.
Author contribution statement
All authors contributed equally to the paper.
Appendix A
Details on the PUIREX experiment
PHENIX is an experimental reactor as well as an electricity production plan. It started in 1973 with a 565 MWth power which was reduced to 350 MWth in the 1990s. PHENIX is a pool-type sodium-cooled fast reactor. The primary circuit is composed of three pumps and four intermediate sodium-sodium heat exchangers connected to two secondary circuits (see Fig. A.1).
 |
Fig. A.1. Schematic view of the PHENIX reactor. |
It has a purification circuit with cold traps and a decay heat emergency system which consists of a water loop around the primary pool. Each secondary circuit includes a pump, a steam generator, and a purification circuit. Under nominal conditions, the sodium temperature in the primary circuit is 520°C, the rotational frequency of the primary pumps is 540 rpm and the speed of the secondary pumps is 700 rpm. The purification circuit is operated with its cold traps. The tertiary circuit is operated as well. Just before the test, the reactor was operated under nominal conditions but cold traps were by-passed. Then, a quick shutdown was carried out, and the sodium temperature plummeted from 520°C to 368°C. An hour after the shutdown, the tertiary circuits were drained. The speed of the primary pumps was reduced from 540 to 300 rpm and down to 110 rpm after two days of cooling. Both secondary circuits were operated at the beginning of the experiment but one was emptied after five days of cooling. Those two events (after 2 and 5 days of cooling) led to discontinuities in the temperature evolution. One and a half hours after the shutdown, the reactor was considered to be in isothermal conditions and behaved as a calorimeter.
In this test, the measured quantity is the sodium temperature in the primary circuit. The decay heat of the entire core is derived from the measurement through the energy balance of equation (A.1) where DH stands for decay heat, Plosses is the inertia depending on the temperature of the sodium θ, Psources are the sources of power and Plosses the losses of power.
The sources and losses terms are derived from a model which depends on the temperature. Knowing the masses of the studied system, the inertia can be computed following equation (A.2) where Mi is the mass of the ith reactor component and Cpi is its heat capacity.
The masses contributing to the total inertia I(θ) are the sodium in the primary circuit (800 tons) and in the secondary circuit (200 tons), the fuel (16 tons), the steel (980 tons) in the sub-assemblies and pins, vessel, structures, pipes, pumps, exchangers, etc. and the graphite in the core neutron shielding (75 tons).
The sources of power are the heat produced by the primary and secondary pumps. The losses of power in the form of radiation and conduction phenomena in the pipes are due to the decay heat emergency system and reactor slab in the primary circuit, and to residual losses in the steam generator in the secondary circuit.
The entire core was equipped with thermocouples in order to measure the sodium temperature and its homogeneity and to check the thermal behavior of the system.
The uncertainty associated with the decay heat derived from equation (A.1) was determined by deterministic propagation of the input parameters uncertainties: ±5% in the calculation of the inertia, 5% due to the pumps, 10% set for the losses in the primary and secondary circuits. The uncertainty associated with the thermocouples is equal to 1.4°C and the uncertainty of the rate of change of the temperature is calculated from the dispersion values of the 13 thermocouples and is equal to 0.5%. The final uncertainty to be taken on the experimental decay heat is between 5 and 11% at one standard deviation depending on the cooling time. The major contributors are the losses and the sodium inertia.
The previous decay heat measurements on PHENIX and SUPERPHENIX concerned cooling times that do not exceed 3 days, and they were all interpreted with older generations of codes and libraries between 1979 and 2002. The PUIREX experiment performed in 2008 was interpreted with the ERANOS-DARWIN2.3 package and the JEFF-3.1.1 library in 2012 [332]. The comparison of the decay heat values for the PUIREX experiment derived from the measurements to the calculated decay heat with the ERANOS-DARWIN2.3 package and the JEFF-3.1.1 library is shown in Figure A.2.
The decay heat of the PHENIX reactor is predicted within a ±8% discrepancy between 1.5 hours and 12 days. These discrepancies are below the experimental uncertainty except for the first day. Figure A.2 also suggests a systematic bias as the discrepancy decreases steadily.
The fuel is the main contributor to the total decay heat, compared to the sodium or steel structures in the vessel. Fission products represent more than 60% of the decay heat, heavy nuclides about 10% around 12 days of cooling (curium and 239Np contributions), and 30% around 1 day (239U and 239Np). The activated steel structures contribute to less than 10% of the total decay heat. The contribution of the internal storage accounting for assemblies placed at the core edges in order to be cooled before unloaded does not exceed 5%. The sodium contribution is negligible.
Appendix B
Details on decay heat formula
B.1. Borst-Wheeler function, circa 1946
The Borst-Wheeler function is an approximate and useful expression providing the total power emitted by fission products, given a number of assumptions. It is also called the Wigner-Way formula, based on rough approximations [38]. Such expression can for instance be found explicitly in reference [2]. It provides the total power P(t, T) emitted by fission products, in the form of β and γ-ray emissions, for a reactor operated for T seconds at a constant power P0, and for a cooling time of t seconds after shutdown.
If β(t) and γ(t) represent the average energy emitted by β and γ-ray emissions, for t seconds after one fission event, one can use the following expressions:
According to reference [2], such expressions are valid from about t = 1 second to t = 106 seconds (or almost 12 days), and their integrations lead to the total power P(t, T). Indeed, the total average energy emitted is the sum of equations (B.1) and (B.2), being approximate to 2.7 × t−1.2; with the additional approximation that the recoverable energy per fission is 200 MeV, the expression of P(t, T) for a reactor of P0 Watts becomes
Equation (B.5) corresponds to the one mentioned in reference [2], and is widely used in reactor physics.
The origin of the semi-empirical equations (B.1) and (B.2) can be traced back to the 40s, as presented in reference [333]. The original experiments were performed prior to 1946 and presented to the American Physical Society in Chicago in June 1946 (recorded on page 115 of volume 70 of the Physical Review, July 1946), but the available documentation can be found in reference [38] from 1948. It is interesting to note that reference [333] presents a number of disagreements between the results from the Borst-Wheeler formula and other values from the Naval Radiological Defense Laboratory.
Although the type of fuel is not mentioned for the applicability of equation (8), it is based on a recoverable energy per fission of 200 MeV, close to the one for 235U (about 202 MeV).
B.2. Untermyer-Weills function, 1952
The report from Untermyer and Weills [67] presents an empirical function for the decay heat of irradiated uranium, from 0.1 second up to 108 seconds (about 3.2 years). It is based on the analysis of measured data, provided in a series of other reports, using a calorimeter as well as radiochemical measurements, combined with calculations for the decay of 239U and 239Np. The justification for propose a different function than equation (8) is that such an equation is based on a statistical analysis of measurements, which might not hold for short and long cooling times. Untermyer and Weills propose the following “experimental data fit”, over the entire available range:
with, as previously all times in seconds, t being the time since the operation (cooling time), T the operation time, P0 the reactor constant power. Reference. [67] also provides an estimate of accuracy (using the reference’s vocabulary):
-
t < 1 second: large error
-
1 < t < 102 seconds: ± 50%
-
102 < t < 104 seconds: ± 30%
-
104 < t < 106 seconds: ± 10%
-
106 < t < 108 seconds: ± 50%.
B.3. Patterson-Schlitz function, 1955
The function for the decay heat proposed by Patterson and Schlitz in reference [334] is similar to the one of Untermyer and Weills, presented in equation (B.6). No further information is available.
B.4. Glasstone function, 1963
Two different expressions can be found in reference [129], with specific ranges of applicability. The solutions proposed in this reference also follow a pragmatic approach, given that the emission rates of beta particles and gamma-ray photons can be expressed by means of empirical expressions. It is stated in reference [129] that the accuracy of such expressions is within a factor of two or less (Ref. [38] is used to justify such a statement).
For periods between 10 seconds up to several weeks after fission, the beta and gamma emission rates for one fission are presented as
(considering that about 0.4 MeV are emitted by beta particles), and
(considering that the photon energy is about 0.7 MeV). The total energy released by beta particles and photons is given by the sum of (B.8) and (B.10). The total energy observed at a time t after shutdown, due to the emission during an interval dT is then given by 2.8 × 10−6t−1.2, given in MeV/sec These expressions are very close to equations (B.1) and (B.2) (although with the values for β and γ being exchanged), and leads to the same value of P(t, T) from equation (8). It is mentioned that this expression can be applied for cooling time above 10 seconds, and it is assumed that it is applicable to reactor with a constant power.
Another expression is also given in reference [129], for shorter cooling time (from 1 sec upwards), and is obtained from the original work of Untermyer and Weills [67].
B.5. El-Wakil function, 1971
A different equation was proposed by M.M. El-Wakil for the decay heat, which is to be relevant for t > 200 seconds [335]:
No additional information is available.
B.6. Glasstone function, 1981
In the new edition of his book [129, 132], Glasstone proposed a new approximation, based on the ANS standard (from 1971, or 1973, or 1979 ?):
where a and b are two constants which depend on the time after shutdown t (see Table B.1).
Parameter values for a and b as a function of the time after shutdown t for equation (B.12).
It is indicated that such fit follows that ANS recommendation within ±6%.
B.7. Todreas-Kazimi function, 1990
The expressions provided in reference [130] by Todreas and Kazimi basically refer to Glasstone (1963) for the decay heat from fission products and actinides decays. But they also present a practical expression for the decay heat due to delayed neutrons. In this case, solving neutron kinetic equations with a large negative insertion of reactivity leads to such decay heat value, expressed as Pdelayed neutrons(t, T):
This expression is valid using typical quantities for 235U fuel, in the case of a water-moderated reactor. Due to the exponential values, the second term is negligible after 0.01 seconds, and the decay heat due to delayed neutrons exponentially decays over a period of about 80 seconds.
In the case of the decay heat from fission products and actinides, reference [130] proposes the same expressions for β(t) and γ(t) as Glasstone [129], leading to equation (8).
Appendix C
A numerical simulation on Bremsstrahlung Ray Measurement for β-decay in Spent Nuclear Fuel: a Japanese example
This work on the simulation of Bremsstrahlung measurements was presented in detail in reference [336]. In Japan, dry storage of a spent nuclear fuel assembly (FA) is not allowed during a pre-determined time length after it is discharged from the core. Mainly due to the limitation of surface temperature of the fuel cladding, the time length is 15 years for an FA of which the maximum discharge burn-up is 48 GWd/t, for example. The time length is too conservative for a spent FA with lower burn-up. Then we proposed to allow storing FA in a dry cask provided the residual heat decays below a limitation value. The residual heat is estimated based on the reactor record and a burn-up calculation. Then we need validation of the residual heat estimation. However, it costs so much to equip a calorimeter to SFPs of every NPP. Then we consider applying gamma-ray spectroscopy to assess the decay heat. Currently, we can quantify the radioactivities of 137Cs→137mBa, 134Cs, 154Eu, 106Ru→106Rh, and 144Ce→144Pr. Their relative contribution to the total decay heat is around 40%.
With the ORIGEN-ARP module in SCALE-6.1, we have calculated time-dependent decay heat for FA discharged after from one to four cycles of irradiation in PWR. The burn-up increment per cycle was assigned 13 GWd/t. The relative contribution of 90Sr→90Y to the total decay heat is around 40%, see Figure C.1.
 |
Fig. C.1. Relative contribution of 90Sr→90Y to total decay heat. |
 |
Fig. C.2. Calculated energy deposition in HPGe detector. |
Then we picked up 27 nuclides of which the relative contribution to the total radio activities exceeds 0.01%.Then we prepare a calculation model where a single fuel rod with 2 cm in length and a cylindrical HPGe detector with 8 cm in length and 8 cm in diameter. The distance between the center of the cylindrical rod and the HPGe detector was 20 cm. Then, we assigned the radioactivities of the 27 nuclides homogeneously in the fuel pellets and calculated photon and electron transports with the PHITS code. The source spectra of gamma and beta rays listed in ICRP-107 were used for the calculation. The calculated energy deposition spectra in the HP-Ge detector 13 years after discharge from the core are shown in Figure C.2.
In addition to peak gamma rays from 134, 137Cs, 154Eu, 144Pr, and 106Rh, the count rate of the Bremsstrahlung ray is significant, especially in the pulse height range from 1.5 to 1.8 MeV. The relative contribution of Bremsstrahlung ray from 90Y to the total count rate in pulse height region from 1.6 to 1.7 MeV is plotted in Figure C.3.
 |
Fig. C.3. Relative contribution of Bremsstrahlung ray from beta decay of 90Y to the total count rate in the pulse height region from 1.6 to 1.87 MeV. |
For the cooling times of 13 years, the contribution is greater than 94% and that is almost independent of the burn-up. Also, for FAs irradiated more than or equal to two cycles, the summation of the
contributions of 90Sr→90Y, 106Ru→106Rh, and 144Ce→144Pr reaches 98%. The radioactivities of 90Sr→90Y can be quantified by the count rate of the pulse height region from 1.6 to 1.7 MeV and the peak count rates of 106Rh and 144Pr gamma rays. Summation of the relative contribution of 90Sr→90Y, 137Cs→137mBa, 134Cs, 154Eu, 106Ru→106Rh, and 144Ce→144Pr to the total decay heat is 80%. Therefore, focusing on the Bremsstrahlung rays from the beta decay of 90Y, the decay heat estimation by photon spectrum measurement might become more credible.
Appendix D
Tables for TAGS data
List of nuclei updated in JEFF-3.1.1 with the Greenwood’s TAGS mean decay energy for light particle component (ELP). The values from the different versions of JEFF and ENDF/B libraries are also included for comparison.
List of nuclei updated in JEFF 3.1.1 with the Greenwood’s TAGS mean decay energy for the electromagnetic component (EEM). The values from the different versions of JEFF and ENDF/B libraries are also included for comparison.
List of nuclei measured per the Total Absorption Gamma Spectroscopy method per the TAS and MTAS collaborations with the associated mean decay energy for light particle (ELP). The values from the different versions of JEFF, JENDL and ENDF/B libraries are also included for comparison. The TAGS values already included in the different versions of libraries are in grey.
List of nuclei measured per the Total Absorption Gamma Spectroscopy method per the TAS and MTAS collaborations with the associated mean electromagnetic decay energy (EEM). The values from the different versions of JEFF, JENDL and ENDF/B libraries are also included for comparison.The TAGS values already included in the different versions of libraries are in grey.
References
- A. Bevilacqua, J.P. Carreton, A. Guskov, T. Hornebrant, C. Jones, Y. Kumano, et al. Storage of Spent Nuclear Fuel, specific safety guide. (International Atomic Energy Agency, IAEA, Vienna, Austria, 2020), SSG-15, Rev. 1. https://www-pub.iaea.org/MTCD/publications/PDF/P1882_web.pdf [Google Scholar]
- J.R Lamarsh, Introduction to Nuclear Reactor Theory (Addison-Wesley Publishing Company, 1966) [Google Scholar]
- C. Poinssot, P. Toulhoat, J.P. Grouiller, J. Pavageau, J.P. Piron, M. Pelletier, et al. Synthesis on the Long Term Behavior of Spent Nuclear Fuel - Volume 1 and 2 (Commissariat à l’Energie Atomique, CEA, 2001). https://inis.iaea.org/collection/NCLCollectionStore/_Public/33/009/33009840.pdf [Google Scholar]
- B. Duchemin, c. Nordborg, Decay heat calculation, An international Nuclear code comparison. Nuclear Energy Agency, NEACRP-319 and NEANDC-275; 1990. https://inis.iaea.org/collection/NcLCollectionStore/_Public/22/009/22009691.pdf [Google Scholar]
- NEA committees on reactor physics and nuclear data. Proceedings of a specialists’ meeting on Data for Decay Heat Predictions (Nuclear Energy Agency, NEACRP-302 and NEANDC-245, 1987). https://www.oecd-nea.org/upload/docs/application/pdf/2020-01/neacrp-l-1987-302.pdf [Google Scholar]
- c. Nordborg, NEACRP/NEANDC Task Force Meeting on Decay Heat Predictions (Nuclear Energy Agency, EACRP-A-1039 and NEANDC-A- 26, 1989). https://www.oecd-nea.org/upload/docs/application/pdf/2020-07/neacrp-a-1989-1039.pdf. [Google Scholar]
- M.A Kellett, A.L. Nichols, O. Bersillon, H. Henriksson, R. Jacqmin, B. Roque, et al. Assessment of Fission Product Decay Data for Decay Heat calculations, A report by the Working Party on International Evaluation co-operation of the NEA Nuclear Science committee, 2007. ISBN 978-92-64-99034-0. [Google Scholar]
- Decay heat of spent nuclear fuels, Accessed: 2022-09-01, https://www.oecd-nea.org/download/wpncs/sg12/ [Google Scholar]
- K. Asfaw, K. Kamimura, T. Nakajima, S. Schultz, P. Shaw, K. Sim, et al. Design of the Reactor core for Nuclear Power Plants (International Atomic Energy Agency, IAEA, Vienna, Austria, 2019). https://www-pub.iaea.org/MTCD/publications/PDF/PUB1859web.pdf [Google Scholar]
- S.J Baik, J. Beard, E. courtin, N. Fil, M. Gasparini, c. Jackson, et al. Design of the Reactor coolant System and Associated Systems for Nuclear Power Plants (International Atomic Energy Agency, IAEA, Vienna, Austria, 2020). https://www-pub.iaea.org/MTCD/publications/PDF/PUB1878_web.pdf [Google Scholar]
- G. Ilas, J. Burns, LWR Decay Heat Analysis with SCALE 6.3 and ENDF/B-VIII.0 Nuclear Data Libraries (International conference TopFuel 2021, Santander, Spain, October 2021), pp. 24–28 [Google Scholar]
- H. Akkurt, H. Liljenfeldt, G. Ilas, S. Baker, Phenomena Identification and Ranking Table (PIRT) for Decay Heat (Electric Power Research Institute, EPRI, USA, 2020), 3002018440 [Google Scholar]
- T. Yamamoto, D. Iwahashi, Validation of decay heat calculation results of ORIGEN2.2 and cASMO5 for light water reactor fuel, J. Nucl. Sci. Technol. 53, 2108 (2016). https://doi.org/10.1080/00223131.2016.1183528 [CrossRef] [Google Scholar]
- A. Shama, D. Rochman, S. caruso, A. Pautz, Validation of spent nuclear fuel decay heat calculations using Polaris, ORIGEN and cASMO5, Ann. Nucl. Energy. 165, 108758 (2022). https://www.sciencedirect.com/science/article/pii/S0306454921006344 [CrossRef] [Google Scholar]
- P. Jansson, M. Bengtsson, U. Bäckström, F. Àlvarez-Velarde, D. calic, S. caruso, et al. Blind Benchmark Exercise for Spent Nuclear Fuel Decay Heat, Nucl. Sci. Eng. 196, 1125 (2022) [CrossRef] [Google Scholar]
- F. Laugier, c. Diop, S. Ebalard, c. Garzenne, A. Sargeni, A new decay heat standard proposition based on a technical specifications guide for computation codes. In: Proc. Int. conf. PHYSOR 2008, Interlaken, Switzerland, 14–19 September (2008) [Google Scholar]
- J.c Wagner, Spent Nuclear Fuel Disposition (Idaho National Laboratory, USA, 2016) [Google Scholar]
- IAEA, Management of Spent Fuel from Nuclear Power Reactors Learning from the Past, Enabling the Future (International Atomic Energy Agency, Vienna, Austria, 2019). http://www.iaea.org/bulletin [Google Scholar]
- NWMO, What is used Nuclear Fuel? (Nuclear Waste Management Organization, Ontario, canada, 2022). https://www.nwmo.ca [Google Scholar]
- ASTM american standards, Standard Guide For characterization Of Spent Nuclear Fuel In Support Of Interim Storage, Transportation And Geologic Repository Disposal (American Nuclear Society; 2021), ASTM c1682-21. https://webstore.ansi.org/Standards/ASTM/astmc168221 [Google Scholar]
- IAEA. Joint convention on the Safety of Spent Fuel Management and on the Safety of Radioactive Waste Management (IAEA International Law Series, 2006) [Google Scholar]
- DIN Standards committee Materials Testing, calculation of the decay power in nuclear fuels of light water reactors - Part 1: Uranium oxide nuclear fuel for pressurized water reactors, English translation of DIN 25463-1:2014-02 (DIN Standards committee Materials Testing, Germany, 2014) [Google Scholar]
- FSC-6910, Decay Heat. In: DOE Fundamentals Handbook, No. DOE-HDBK-1012/2-92 in 1 (U.S., Department of Energy, 1992) [Google Scholar]
- Technical committee ISO/TC 85, Nuclear energy, Sub-committee SC 3, Power Reactor Technology, Nuclear Energy - Light Water Reactors - calculation of the Decay Heat Power in Nuclear fuels (ISO International Standard, 1992) [Google Scholar]
- DIN Standards committee Materials Testing. calculation of the Decay Power in Nuclear Fuels of Light Water Reactors - Part 2: Mixed-uranium-plutonium oxide (MOX) nuclear fuel for pressurized water reactors, English translation of DIN 25463-2:2014-02 (DIN Standards committee Materials Testing, Germany, 2014) [Google Scholar]
- American Nuclear Society Standards committee Working Group ANS-5 1. Decay Heat Power in Light Water Reactors (American Nuclear Society, 2014), ANSI/ANS-5.1-2014 [Google Scholar]
- Technical committee ISO/TC 85, Nuclear energy, Sub-committee SC 6, Power Reactor Technology. Nuclear Energy - Light Water reactors - calculation of the Decay Heat Power in Nuclear Fuels (ISO International Standard, 2022), ISO 10645:2022 [Google Scholar]
- A. Sotomayor-Rivera, Spent Fuel Heat Generation in an Independent Spent Fuel Storage Installation (U.S. Nuclear Regulatory commission, USA, 2018), US NRC Regulatory Guide 3.54, Rev.2 [Google Scholar]
- Fuel Burnup, Accessed: 2022-06-23, https://www.nuclear-power.com/nuclear-power/reactor-physics/reactor-operation/fuel-burnup/ [Google Scholar]
- M. Aissa, Fuel Burnup Plant Records: Generation and Accuracy, In: Proceedings of International Workshop on Advances in Applications of Burnup credit for Spent Fuel Storage, Transport, Reprocessing, and Disposition, 27-30 October. cordoba, Spain (2009). https://www.oecd-nea.org/science/wpncs/buc/workshop-2009/ [Google Scholar]
- B.B Bevard, J.c. Wagner, c.V. Parks, M. Aissa, Review of Information for Spent Nuclear Fuel Burnup confirmation (Oak Ridge National Laboratory, USA, 2009), NUREG/cR-6998 [Google Scholar]
- F. Michel-Sendis, I. Gauld, J.S. Martinez, c. Alejano, M. Bossant, D. Boulanger, et al. SFCOMPO-2.0: An OECD NEA database of spent nuclear fuel isotopic assays, reactor design specifications, and operating data, Ann. Nucl. Energy 110, 779 (2017). https://www.sciencedirect.com/science/article/pii/S0306454917302104 [CrossRef] [Google Scholar]
- D. Rochman, A. Vasiliev, H. Ferroukhi, M. Hursin, R. Ichou, J. Taforeau, et al. Analysis for the ARIANE GU3 sample: nuclide inventory and decay heat, EPJ Nucl. Sci. Technol. 7, 14 (2021). https://doi.org/10.1051/epjn/2021013 [CrossRef] [EDP Sciences] [Google Scholar]
- D. Rochman, F. Álvarez-Velarde, R. Dagan, L. Fiorito, S. Häkkinen, M. Kromar, et al., On the estimation of nuclide inventory and decay heat: a review from the EURAD European project, EPJ Nucl. Sci. Technol. 9, 14 (2023). https://doi.org/10.1051/epjn/2022055 [CrossRef] [EDP Sciences] [Google Scholar]
- K.S Smith, S. Tarves, T. Bahadir, R. Ferrer, Benchmarks for Quantifying Fuel Reactivity Depletion Uncertainty (Electric Power Research Institute, EPRI, USA, 2011), p. 1022909 [Google Scholar]
- S. Børresen, A. Becker, calculation of neutron emission from spent LWR fuel assemblies: SNF method and validation, In: International conference on Reactor Physics, Nuclear Power: A Sustainable Resource, September 14-19. Interlaken, Switzerland (2008) [Google Scholar]
- P. Schillebeeckx, M. Verwerft, P. Romojaro, G. Žerovnik, N. Messaoudi, G. Alaerts, et al. An absolute measurement of the neutron production rate of a spent nuclear fuel sample used for depletion code validation, Front. Energy Res. 11, 1162367 (2023). https://www.frontiersin.org/articles/10.3389/fenrg.2023. [CrossRef] [Google Scholar]
- K. Way, E.P. Wigner, The Rate of Decay of Fission Products, Phys. Rev. 73, 1318 (1948). https://link.aps.org/doi/10.1103/PhysRev.73.1318 [CrossRef] [Google Scholar]
- Y. Liu, B. Kochunas, W. Martin, T. Downar, Delayed fission energy effect on LWR normal operation and transients, Ann. Nucl. Energy 128, 84 (2019). https://www.sciencedirect.com/science/article/pii/S0306454918307126 [CrossRef] [Google Scholar]
- O.W Hermann, c.V. Parks, J.P. Renier, Technical Support for a Proposed Decay Heat Guide Using Sas2H/Origen-S Data (Oak Ridge National Laboratory, 1994), NREG/cR-5625, ORNL-6698. https://www.osti.gov/servlets/purl/43752 [Google Scholar]
- U.S NRC, Spent Fuel Heat Generation in an Independent Spent Fuel Storage Installation, U.S. Nuclear Regulatory commission, USA, US NRC Regulatory Guide 3.54, Rev.1., 1999. https://www.nrc.gov/docs/ML0037/ML003761667.pdf [Google Scholar]
- I.c Gauld, J.c. Ryman, Nuclide Importance to criticality Safety, Decay Heating, and Source Terms Related to Transport and Interim Storage of High-Burnup LWR Fuel (Oak Ridge National Laboratory, USA, 2001) [Google Scholar]
- G. Žerovnik, P. Schillebeeckx, K. Govers, A. Borella, D. Ćalić, L. Fiorito, et al. Observables of interest for the characterisation of Spent Nuclear Fuel (Publications Office of the European Union, Luxembourg, 2018), EUR 29301 EN, ISBN 978-92-79-90347-2 [Google Scholar]
- A. Tobias, Decay heat, Prog. Nucl. Energy 5, 1 (1980). https://www.sciencedirect.com/science/article/pii/0149197080900025 [CrossRef] [Google Scholar]
- F. Storrer, Review of Decay Heat Predictions and Standards (Meeting of the JEF Working Group on Radioactive Decay and Fission Yield Data, BNFL Office, London, UK., 1994), JEF/DOC-473 [Google Scholar]
- K. Shure, Decay Heat and Decay Rate of Actinides in Highly Neutron-Irradiated Uranium Initially of High 235U content, Nucl. Sci. Eng. 85, 51 (1983). https://doi.org/10.13182/NSE83-A17151 [CrossRef] [Google Scholar]
- T.R England, W.B. Wilson, TMI-2 Decay Power: LASL Fission-Product and Actinide; Decay Power calculations for the President’s commission on the Accident at Three Mile Island TMI-2 (Los Alamos Scientific Laboratory, NM, USA, 1979) LA-8041-MS. https://inis.iaea.org/collection/NCLCollectionStore/_Public/11/528/11528011.pdf [Google Scholar]
- H. Smith, The Relative Significance of Actinide Decay Heat for Nuclear Fuel characterization, In: Transactions of the American Nuclear Society, Vol. 85, 2001 Winter Meeting, Reno, Nevada (2001), p. 318 [Google Scholar]
- K. Tasaka, J. Katakura, T. Yoshida, T. Kato, R. Nakasima, Recommended values of decay heat power and method to utilize the data (Japan Atomic Energy Research Institute, 1991), JAERI-M 91-034 [Google Scholar]
- J.H Mairs, S. Nair, The Inventories of Actinides and Fission Product Arising in Spent Nuclear Fuel: Results Using the Rice code (Berkeley Nuclear Labs, USA, 1979), cEGB-RD-B-N-4579 [Google Scholar]
- D.H Stoddard, E.L. Albenesius, Radiation Properties of 238Pu Produced for Isotopic Power Generators (Savannah River Laboratory, USA, 1965), TID-4500. https://www.osti.gov/servlets/purl/4616364 [Google Scholar]
- I.c Gauld, B.D. Murphy, Proposed Expansion of Regulatory Guide 3.54-Decay Heat Generation in an Independent Spent Fuel Storage Installation (Oak Ridge National Laboratory, 2010) ORNL/TM-2007/231 [Google Scholar]
- M.W Francis, c.F. Weber, M.T. Pigni, I.c. Gauld, Reactor Fuel Isotopics and code Validation for Nuclear Applications (Oak Ridge National Laboratory, USA, 2014), ORNL/TM-2014/464 [Google Scholar]
- K. Debertin, H. Ramthun, FPND needed for Nondestructive Burnup Determination, In: Proceedings of a panel on fission product nuclear data organized by the International Atomic Energy Agency, November 26-30. Bologna, Italy (1974). https://www-nds.iaea.org/publications/tecdocs/iaea-0169-volume3.pdf [Google Scholar]
- D. Rochman, J. Taforeau, T. Simeonov, A. Shama, comparison of calculated and measured spent nuclear fuel decay heat with cASMO5, SNF and standard methods, Nucl. Eng. Design 410, 112392 (2023). https://www.sciencedirect.com/science/article/pii/S0029549323002418 [CrossRef] [Google Scholar]
- B.L Broadhead, M.D. Dehart, J.c. Ryman, J.S. Tang, c.V. Parks, Investigation of Nuclide Importance to Functional Requirements Related to Transport and Long-Term Storage of LWR Spent Fuel (Oak Ridge National Laboratory, 1995), ORNL/TM-12742 [Google Scholar]
- K. Tasaka, J. Katakura, T. Yoshida, Recommended values of decay heat power and method to utilize the data (Japan Atomic Energy Research Institute (JAERI), Japan, 1991), JAERI-M 91-034, NEANDC(J)-161/U and INDC(JPN)-149/L [Google Scholar]
- A.J.M. Plompen, O. cabellos, c. De Saint Jean, M. Fleming, A. Algora, M. Angelone, et al., The joint evaluated fission and fusion nuclear data library, JEFF-3.3, Eur. Phys. J. A 56, 181 (2020). https://doi.org/10.1140/epja/s10050-020-00141-9 [CrossRef] [Google Scholar]
- F.P Roberts, The Radiation characteristics of Reactor Produced Rhodium, Palladium, Ruthenium and Technetium (Pacific Northwest Laboratory, Richland, Washington, USA, 1972), BNWL-1693 [Google Scholar]
- Subcommittee on Radiochemistry; Subcommittee on the Use of Radioactivity Standards; committee on Nuclear Science; National Research council, Users’ Guide for Radioactivity Standards (The National Academies Press, Washington, DC, 1974). https://nap.nationalacademies.org/catalog/20179/users-guide-for-radioactivity-standards [Google Scholar]
- S. Nakamura, H. Harada, T. Katoh, Measurement of Thermal Neutron capture cross Section and Resonance Integral of the Reaction 133cs(n,γ) 134m, 134gcs, J. Nucl. Sci. Technol. 36, 847 (1999). https://doi.org/10.1080/18811248.1999.9726275 [CrossRef] [Google Scholar]
- B.F Rider, J.L. Russell Jr., D.W. Harris, J.P. Peterson Jr., The Determination of Uranium Burnup in MWd/ton (Vallecitos Atomic Laboratory General Electric company Pleasanton, california, 1960), GEAP-3373. https://www.osti.gov/servlets/purl/4156626 [Google Scholar]
- D. Harris, J. Epstein, Properties of Selected Radioisotopes (NASA Goddard Space Flight center Greenbelt, MD, US, 1968), NASA SP-7031. https://ntrs.nasa.gov/citations/19680020487 [Google Scholar]
- Practices and Developments in Spent Fuel Burnup credit Applications. No. 1378 in TECDOC Series (cD-ROM). Vienna, Austria: International Atomic Energy Agency, 2003 [Google Scholar]
- S.E Skutnik, Proposed re-evaluation of the 154Eu thermal (n,γ) capture cross-section based on spent fuel benchmarking studies, Ann. Nucl. Energy 99, 80 (2017). https://www.sciencedirect.com/science/article/pii/S0306454916305710 [CrossRef] [Google Scholar]
- Nucleonica GmbH, Nucleonica Nuclear Science Portal, Version 3.0.269, Karlsruhe, 2007. www.nucleonica.com [Google Scholar]
- S. Untermyer, J.T. Weills, Heat Generation in Irradiated Uranium (Argonne National Laboratory, 1953), ANL-4790 [Google Scholar]
- S.E Beall, An experimental determination of fission product heating after shutdown of the low intensity training reactor (Oak Ridge National Laboratory, USA, 1951), ORNL-1075. https://www.osti.gov/servlets/purl/4346759 [Google Scholar]
- J.W Roddy, J.c. Mailen, Radiological characteristics of Light Water Reactor Spent Fuel: a litterature survey of experimental data (Oak Ridge National Laboratory, USA, 1987), ORNL/TM-10105 [Google Scholar]
- F. Schmittroth, A comparison of Measured and calculated Decay Heat for Spent Fuel Near 2.5 years cooling Time (Hanford Engineering Development Laboratory, USA, 1980) TC-1759 [Google Scholar]
- M. McKinnon, c. Heeb, J. creer, Decay Heat Measurements and Predictions of BWR Spent Fuel (Electric Power Research Institute (EPRI), USA, 1986) NP-4619 [Google Scholar]
- M.A McKinnon, J.W. Doman, R.J. Guenther, J.M. creer, c.E. King, in cask Handling Experience and Decay Heat, Heat transfer, and Shielding data (Pacific Northwest Laboratory, Richland, Washington, USA, 1986), Vol. 1 [Google Scholar]
- L.E Wiles, N.J. Lombardo, c.M. Heeb, U.P. Jenquin, T.E. Michener, c.L. Wheeler, et al. in Pre- and Post-test Decay Heat, Heat transfer, and Shielding analysis (Pacific Northwest Laboratory, Richland, Washington, USA, 1986), Vol. 2 [Google Scholar]
- F. Schmittroth, ORIGEN2 calculations of PWR Spent Fuel Decay Heat compared with calorimeter Data (Hanford Engineering Development Laboratory, USA, 1984), HEDL-TME 83-32 (UC-85) [Google Scholar]
- S.B Gunst, D.E. conway, J.c. connor, Measured and calculated Rates of Decay Heat in Irradiated 235U, 233U, 239Pu, and 232Th, Nucl. Sci. Eng. 56, 241 (1975). https://doi.org/10.13182/NSE75-A26738 [CrossRef] [Google Scholar]
- F. Sturek, L. Agrenius, Measurements of decay heat in spent nuclear fuel at the Swedish interim storage facility, clab (Svensk Kärnbränslehantering AB (SKB), Sweden, 2006), R-05-62 [Google Scholar]
- I.c Gauld, G. Ilas, B.D. Murphy, c.F. Weber, Validation of SCALE 5 decay heat predictions for LWR Spent Nuclear Fuel (Oak Ridge National Laboratory, USA, 2010) ORNL/TM-2008/015 and NUREG/cR-6972 [Google Scholar]
- B.D Murphy, I.c. Gauld, Spent fuel Decay Heat Measurements Performed at the Swedish central Interim Storage Facility (Oak Ridge National Laboratory, USA, 2010) ORNL/TM-2008/016 and NUREG/cR-6971 [Google Scholar]
- G. Ilas, I.c. Gauld, H. Liljenfeldt, Validation of ORIGEN for LWR used fuel decay heat analysis with SCALE, Nucl. Eng. Design 273, 58 (2014). https://www.sciencedirect.com/science/article/pii/S0029549314001514 [CrossRef] [Google Scholar]
- P. Jansson, M. Bengtsson, U. Bäckström, K. Svensson, M. Lycksell, A. Sjöland, Data from calorimetric decay heat measurements of five used PWR 17x17 nuclear fuel assemblies, Data Brief 28, 104917 (2020) [CrossRef] [Google Scholar]
- T. Aoyama, S. Nose, S. Suzuki, Measurement and analysis of decay heat of fast reactor spent fuel, In: the proceedings of the 1998 Symposium of nuclear data, november 19-20, JAERI, Tokay, Japan, JAERI-conf 99-002, INDC(JPN)-182/U (1999), p. 84 [Google Scholar]
- S. Maeda, S. Nose, T. Aoyama, Measurement and analysis of JOYO MK-II spent MOX fuel decay heat(2) (JNDC, Tokai-mura, Japan, 2001) JNC TN9400 2001-031 [Google Scholar]
- S. Maeda, T. Aoyama, Decay Heat of Fast Reactor Spent Fuel, J. Nucl. Sci. Technol. 39, 1104 (2002). https://doi.org/10.1080/00223131.2002.10875294 [CrossRef] [Google Scholar]
- S. Maeda, T. Sekine, T. Aoyama, Measurement and analysis of decay heat of fast reactor spent MOX fuel, Ann Nucl. Energy 31, 1119 (2004). https://www.sciencedirect.com/science/article/pii/S0306454903003049 [CrossRef] [Google Scholar]
- G. Gillet, M. Favet, M. Paulin, Measurement of Decay Heat and comparison with Predictions, Nucl. Sci. Eng. 106, 94 (1990). https://doi.org/10.13182/NSE90-A23763 [CrossRef] [Google Scholar]
- J.c Jaboulay, S. Bourganel, Analysis of MERCI Decay Heat Measurement for PWR UO2 Fuel Rod. Nucl. Technol. 177, 73 (2012). https://doi.org/10.13182/NT12-A13328. [CrossRef] [Google Scholar]
- c. Fiche, Mesure de la puissance résiduelle totale émise par les produits de fission thermique de 239Pu et 233U (commissariat à l’Energie Atomique (CEA), 1976) NEACRP/L 212. https://www-nds.iaea.org/media/docs/fission/NEACRP-L-212(1976).pdf [Google Scholar]
- A. Vasile, B. Fontaine, M. Vanier, P. Gauthe, V. Pascal, G. Prulhiere, et al., The PHENIX Final Tests Revue Générale Nucléaire 6, 73 (2010) [Google Scholar]
- c. Blandin, S. Bourganel, L.G. d’Aillon, Merci - Mosaic: Experimental Tools for Residual Power Measurement in the Osiris Reactor, In: Proceedings of the 12th meeting of the International Group On Research Reactors. Beijing, china (2009). https://www.igorr.com/Documents/2009-BEIJING/BLANDIN.pdf [Google Scholar]
- L.G. d’Aillon, MOSAIC patent: Ex-reactor two phase transient nuclear calorimeter; Priority claim number & date: FR/2007/0058626, 2007, October 26 - International publication reference: WO/2009/053456 [Google Scholar]
- E. Brun, F. Damian, c.M. Diop, E. Dumonteil, F.X. Hugot, c. Jouanne, et al., TRIPOLI-4, CEA, EDF and AREVA reference Monte carlo code, Ann. Nucl. Energy 82, 151 (2015). https://www.sciencedirect.com/science/article/pii/S0306454914003843 [CrossRef] [Google Scholar]
- R. Sanchez, I. Zmijarevic, M. coste-Delclaux, E. Masiello, S. Santandrea, E. Martinolli, et al., APOLLO2 Year 2010, Nucl. Sci. Technol. 42, 474 (2010). https://www.koreascience.or.kr/article/JAKO201007535002887.page [Google Scholar]
- A. Tsilanizara, c.M. Diop, B. Nimal, M. Detoc, L. Lunéville, M. chiron, et al., DARWIN: An Evolution code System for a Large Range of Applications, J. Nucl. Sci. Technol. 37, 845 (2000). https://doi.org/10.1080/00223131.2000.10875009 [CrossRef] [Google Scholar]
- S. Lahaye, T.D. Huynh, A. Tsilanizara, comparison of deterministic and stochastic approaches for isotopic concentration and decay heat uncertainty quantification on elementary fission pulse. EPJ Web conf. 111, 09002 (2016). https://doi.org/10.1051/epjconf/201611109002 [CrossRef] [EDP Sciences] [Google Scholar]
- J. Huyghe, V. Vallet, D. Lecarpentier, c. Reynard-carette, c. Vaglio-Gaudard, How to obtain an enhanced extended uncertainty associated with decay heat calculations of industrial PWRs using the DARWIN2.3 package, EPJ Nucl. Sci. Technol. 5, 8 (2019). https://doi.org/10.1051/epjn/2019002 [CrossRef] [EDP Sciences] [Google Scholar]
- K. Johnston, A calorimetric determination of fission product heating in fast reactor plutonium fuel. J. Nucl. Energy Parts A/B Reactor Sci. Technol. 19, 527 (1965). https://www.sciencedirect.com/science/article/pii/0368323065901321 [CrossRef] [Google Scholar]
- M. Fleming, J.c. Sublet, Validation of FISPACT-II, decay heat and inventory, predictions for fission events (UK Atomic Energy Authority, 2018) UKAEA-R(18)003. https://www-nds.iaea.org/media/docs/fission/UKAEA-R18003.pdf [Google Scholar]
- P.c Fisher, L.B. Engle, Delayed Gammas from Fast-Neutron Fission of Th232, U233, U235, U238, and Pu239, Phys. Rev. 134, B796 (1964). https://link.aps.org/doi/10.1103/PhysRev.134.B796 [CrossRef] [Google Scholar]
- A. McNair, F.J. Bannister, R.L.G. Keith, H.W. Wilson, A measurement of the energy released as kinetic energy of β-particles emitted in the radioactive decay of the fission products of 235U, J. Nucl. Energy 23, 73 (1969). https://www.sciencedirect.com/science/article/pii/0022310769900379 [CrossRef] [Google Scholar]
- L.R Bunney, D. Sam, Gamma-Ray Spectra of the Products of Thermal-Neutron Fission of 235U at Selected Times after Fission, Nucl. Sci. Eng. 39, 81 (1970). https://doi.org/10.13182/NSE70-A21173 [CrossRef] [Google Scholar]
- T.D MacMahon, R. Wellum, H.W. Wilson, Energy released by beta radiation following fission, Part I – 235U data, J. Nucl. Energy 24, 493 (1970). https://www.sciencedirect.com/science/article/pii/0022310770900286 [CrossRef] [Google Scholar]
- N. Tsoulfanidis, B.W. Wehring, M.E. Wyman, Measurements of Time-Dependent Energy Spectra of Beta Rays from Uranium-235 Fission Fragments, Nucl. Sci. Eng. 43, 42 (1971). [CrossRef] [Google Scholar]
- M. Lott, G. Lhiaubet, F. Dufreche, R. de Tourreil, Puissance résiduelle totale émise par les produits de fission thermique de 235U, J. Nucl. Energy 27, 597 (1973). https://www.sciencedirect.com/science/article/pii/0022310773900208 [CrossRef] [Google Scholar]
- B. Alam, J. Scobie, Measurements of the beta energy release rate at short times after fission in uranium-235, Ann. Nucl. Sci. Eng. 1, 573 (1974). https://www.sciencedirect.com/science/article/pii/0302292774900816 [CrossRef] [Google Scholar]
- S.J Friesenhahn, N.A. Lurie, N.c. Rogers, N. Vagelatos, 235U fission product decay heat from 1 to 105 seconds (Electric Power Research Institute, USA, 1976) EPRI NP-180 [Google Scholar]
- J.L Yarnell, P.J. Bendt, Decay heat from products of 235U thermal fission by fast response boil-off calorimetry (Los Alamos Scientific Laboratory, USA, 1977), LA-NUREG-6713 [Google Scholar]
- J.K Dickens, J.F. Emery, T.A. Love, J.W. Mcconnell, K.J. Northcutt, R.W. Peele, et al., Fission-Product Energy Release for times following thermal-neutron fission of 235U between 2 and 14,000 seconds (Oak Ridge National Laboratory, USA, 1977) ORNL/NUREG-14. [Google Scholar]
- P.I Johansson, G. Nilsson, Measurement of decay energy released in thermal fission of 235U (Aktiebolaget Atomenergi, Sweden, 1977) [Google Scholar]
- J.L Yarnell, P.J. Bendt, calorimetric fission product decay heat measurements for 239Pu, 233U and 235U (Los Alamos Scientific Laboratory, USA, 1978) LA-7452-MS [Google Scholar]
- V.E Schrock, L.M. Grossman, S.G. Prussin, K.c. Sockalingam, F. Nuh, c.K. Fan, et al., A calorimetric Measurement of Decay Heat from 235U Fission Products from 10-105 Seconds (Electric Power Research Institute, USA, 1978) NP-616 [Google Scholar]
- S.J Friesenhahn, N.A. Lurie, Measurements of 239Pu and 235U fission product decay power from 1 to 105 seconds (Electric Power Research Institute, USA, 1979), EPRI NP-998. https://www-nds.iaea.org/media/docs/fission/EPRI-NP-180(1976).pdf [Google Scholar]
- E.T Jurney, P.J. Bendt, T.R. England, Fission product gamma spectra (Los Alamos Scientific Laboratory, USA, 1979), LA-7620-MS [Google Scholar]
- J.K Dickens, T.A. Love, J.W. Mcconnell, R.W. Peele, Fission-Product Energy Release for Times Following Thermal-Neutron Fission of 235U Between 2 and 14 000 s. Nucl. Sci. Eng. 74, 106 (1980). https://doi.org/10.13182/NSE80-A19627 [Google Scholar]
- J.K Dickens, T.A. Love, J.W. Mcconnell, R.W. Peele, Fission-Product Energy Release for Times Following Thermal-Neutron Fission of Plutonium-239 and Plutonium-241 Between 2 and 14 000 s. Nucl. Sci. Eng. 78, 126 (1981). https//doi.org/10.13182/NSE81-A20099 [Google Scholar]
- J.K Dickens, J.F. Emery, T.A. Love, J.W. Mcconnell, K.J. Northcutt, R.W. Peele, et al. Fission-Product Energy Release for times following thermal-neutron fission of 239Pu between 2 and 14 000 seconds (Oak Ridge National Laboratory, USA, 1978a), ORNL/NUREG-34. [Google Scholar]
- J.K Dickens, J.F. Emery, T.A. Love, J.W. Mcconnell, K.J. Northcutt, R.W. Peele, et al., Fission-Product Energy Release for times following thermal-neutron fission of 241Pu between 2 and 14 000 seconds (Oak Ridge National Laboratory, USA, 1978b), ORNL/NUREG-47 [Google Scholar]
- M. Akiyama, S. An, Gamma Decay Heat for 14 MeV Neutron Fission of 235U, 238U, and 232Th, In: NEANDC Specialists Meetings on Yields and Decay Data of Fission Product Nuclides, October 24-27, 1983 (Brookhaven National Laboratory, USA, 1984), BNL-5177 [Google Scholar]
- I. Gauld, Data compilation and Analysis of Fission Product Decay Heat Experiments (International Atomic Energy Agency, 2019), TAL-NAPC20190311-001. https://www-nds.iaea.org/media/docs/fission/Gauld_SummaryReport_2019.pdf [Google Scholar]
- V.E Schrock, L.M. Grossman, S.G. Prussin, K.c. Sockalingam, F. Nuh, c.K. Fan, et al., A calorimetric measurement of decay heat from 235U fission products from 10 to 105 seconds (Electric Power Research Institute, USA, 1978), EPRI NP-616. https://www-nds.iaea.org/media/docs/fission/EPRI-NP-616(1978).pdf [Google Scholar]
- P.I Johansson, Integral determination of the β and γ heat in thermal-neutron-induced fission of 235U and 239Pu, and the gamma heat in the fast fission of 238U. In: Proceedings of a Specialists’ meeting on data for decay heat predictions, Studsvik, Sweden, 7-10 September (1987). https://www.oecd-nea.org/upload/docs/application/pdf/2020-01/neacrp-l-1987-302.pdf [Google Scholar]
- A. McNair, R.L.G. Keith, A measurement of the β decay energy from the fission products of 239Pu, J. Nucl. Energy 23, 697 (1969). https://www.sciencedirect.com/science/article/pii/0022310769900252 [CrossRef] [Google Scholar]
- A. Tobias, Decay Heat (central Electricity Generating Board, Berkeley Nuclear Laboratories, Berkeley, Gloucestershire, GL13 9PB, 1979) [Google Scholar]
- M. Akiyama, S. An, Measurements of fission product decay heat for fast reactors, In: Proceedings of the International conference on Nuclear Data for Science and Technology, Antwerp 6-10 September 1982 (1983) [Google Scholar]
- W.A Schier, G.P. couchell, β and γ decay heat measurements between 0.1 sec - 50,000 sec for neutron fission of 235U, 238U and 239Pu: final report (University of Massachussetts Lowell, 1997) DOE/ER/40723-4. https://doi.org/10.2172/532606 [Google Scholar]
- H.V Nguyen, Gamma-ray Spectra and Decay Heat Following 235U Thermal Neutron Fission (University of Massachusetts Lowell, Lowell, USA, 1997) [Google Scholar]
- S. Li, Beta Decay Heat Following 235U, 238U and 239Pu Neutron Fission (University of Massachusetts Lowell, Lowell, USA, 1997) [Google Scholar]
- E.H Seabury, Gamma-ray Decay Heat Measurements Following 238U(n,f) and 239Pu(n,f) (University of Massachusetts Lowell, Lowell, USA, 1997) [Google Scholar]
- Y. Nauchi, H. Junichi, S. Tadafumi, T. Yoshiyuki, K. Koji, U. Hironobu, Detection of Gamma Ray from Sort-Lived Fission Products at KUCA and KURNS-LINAC, In: Symposium on Nuclear Data 2020, 26-27 November 2020, RIKEN Wako campus (2020). https://indico2.riken.jp/event/3359/contributions/15415/ [Google Scholar]
- S. Glasstone, A. Sesonske, Nuclear Reactor Engineering (D. Van Nostrand company, 1963) [Google Scholar]
- N.E Todreas, M.S. Kazimi, Nuclear Systems I, Thermal Hydraulic Fundamentals (Hemisphere Publishing corporation, 1990) [Google Scholar]
- J.J Duderstadt, L.J. Hamilton, Nuclear Reactor Analysis (John Wiley & sons, 1976) [Google Scholar]
- S. Glasstone, A. Sesonske, Nuclear Reactor Engineering, 3rd edn. (Krieger Publishing company, 1981) [Google Scholar]
- J.c Nimal, Sûreté et puissance résiduelle (commissariat à l’Énergie Atomique (CEA), France, 2001), clefs du CEA numéro 45. https://www.cea.fr/multimedia/Documents/publications/clefs-cea/archives/fr/08-puissance.pdf [Google Scholar]
- H.L Hall, D.c. Hoffman, Delayed fission. Annu. Rev. Nucl. Part. Sci. 42, 147 (1992). https://www.annualreviews.org/doi/pdf/10.1146/annurev.ns.42.120192.001051 [CrossRef] [Google Scholar]
- A.N Andreyev, M. Huyse, P. Van Duppen, colloquium: Beta-delayed fission of atomic nuclei, Rev. Mod. Phys. 85, 1541 (2013). https://link.aps.org/doi/10.1103/RevModPhys.85.1541 [CrossRef] [Google Scholar]
- American Nuclear Society, Decay heat power in Light Water Reactors, ANSI/ANS-5.1-2014 (R2019) (2019) [Google Scholar]
- DIN Standards committee Materials Testing. Decay heat power in nuclear fuels of high-temperature reactors with spherical fuel elements, English translation of DIN 25485:1990-05 (DIN Standards committee Materials Testing, Germany, 1990) DIN 25485:1990-05 [Google Scholar]
- K. Tasaka, T. Katoh, J. Katakura, T. Yoshida, S. Iijima, R. Nakasima, et al., Recommendation on Decay Heat Power in Nuclear Reactors, J. Nucl. Sci. Technol. 28, 1134 (1991). https://doi.org/10.1080/18811248.1991.9731481 [CrossRef] [Google Scholar]
- K. Shure, Fission Product Decay Energy (Bettis Technical Review, USA, 1961) WAPD-BT-24 [Google Scholar]
- J.F Perkins, R.W. King, Energy release from the decay of fission products, Nucl. Sci. Eng. 3, 726 (1958) [CrossRef] [Google Scholar]
- J.R Stehn, E.F. clancy, Fission products radioactivity and heat generation, In: Proceedings of the second UN International conference on the Peaceful Uses of Atomic Energy, Geneva (1958), Vol. 13, p. 49 [Google Scholar]
- J.K Dickens, T.R. England, R.E. Schenter, current status and proposed improvements to the ANSI/ANS-5.1 American National Standard for decay heat power in light water reactors, Nucl. Safety 32, 209 (1991) [Google Scholar]
- V.E Schrock, A Revised ANS Standard for Decay Heat from Fission Products, Nucl. Technol. 46, 323 (1979). https://doi.org/10.13182/NT79-A32334 [CrossRef] [Google Scholar]
- V.E Schrock, Evaluation of decay heating in shutdown reactors, Prog. Nucl. Energy 3, 125 (1979). https://www.sciencedirect.com/science/article/pii/0149197079900131 [CrossRef] [Google Scholar]
- E. Rutherford, F. Soddy, LX. Radioactive Change, London Edinburgh Dublin Philos. Mag. J. Sci. 5, 576 (1903). https://doi.org/10.1080/14786440309462960 [Google Scholar]
- H. Bateman, The solution of a system of differential equations occurring in the theory of radioactive transformations. In: the Proceedings of the Cambridge Philosophical Society, Mathematical and physical sciences (1910), p. 423. https://archive.org/details/cbarchive_122715_solutionofasystemofdifferentia1843/mode/2up [Google Scholar]
- W.M Stacey, Nuclear Reactor Physics (John Wiley & sons, 2001) [Google Scholar]
- A.E Isotalo, J. Leppänen, J. Dufek, Preventing xenon oscillations in Monte Carlo burnup calculations by enforcing equilibrium xenon distribution, Ann. Nucl. Energy 60, 78 (2013). https://www.sciencedirect.com/science/article/pii/S0306454913002405 [CrossRef] [Google Scholar]
- D. Lee, J. Rhodes, K. Smith, Quadratic Depletion Methodfor Gadolinium Isotopes in CASMO-5, Nucl. Sci. Eng. 174, (2013). https://doi.org/10.13182/NSE12-20 [Google Scholar]
- M.A.W. Mondal, M. Doroudian, Burnup calculations to estimate the effect of chemical shim boron on the production and depletion of heavy isotopes in a PWR, Appl. Rad. Isotopes. 45, 155 (1994). https://www.sciencedirect.com/science/article/pii/0969804394900043 [CrossRef] [Google Scholar]
- NEA/WPNCS/EGADSNF, Spent Nuclear Fuel Assay Data for Isotopic Validation (Nuclear Energy Agency, NEA/NSC/WPNCS/DOC(2011)5, 2011) [Google Scholar]
- G. Ilas, I.C. Gauld, SCALE analysis of CLAB decay heat measurements for LWR spent fuel assemblies, Ann. Nucl. Energy 35, 37 (2008). https://www.sciencedirect.com/science/article/pii/S0306454907001375 [CrossRef] [Google Scholar]
- J. Hu, I.C. Gauld, J.E. Banfield, S.E. Skutnik, Developing Spent Fuel Assembly Standards for Advanced NDA Instrument Calibration - NGSI Spent Fuel Project (Oak Ridge National Laboratory, USA, 2014) ORNL/TM-2013/576 [Google Scholar]
- G. Radulescu, I.C. Gauld, G. Ilas, SCALE 5.1 Predictions of PWR Spent Nuclear Fuel Isotopic Compositions (Oak Ridge National Laboratory, USA, 2010) ORNL/TM-2010/44 [Google Scholar]
- G. Ilas, I.C. Gauld, Analysis of Experimental Data for High-Burnup PWR Spent Fuel Isotopic Validation - Vandellos II (Oak Ridge National Laboratory, USA, 2011) ORNL/TM-2009/321 [Google Scholar]
- G. Ilas, I.C. Gauld, G. Radulescu, Validation of new depletion capabilities and ENDF/B-VII data libraries in SCALE, Ann. Nucl. Energy 46, 43 (2012). https://www.sciencedirect.com/science/article/pii/S0306454912000916 [CrossRef] [Google Scholar]
- J.C Wagner, M.D. Dehart, Review of Axial Burnup Distribution Considerations for Burnup Credit Calculations (Oak Ridge National Laboratory, USA, 2000) ORNL/TM-1999/246 [Google Scholar]
- J.C Wagner, M.D. Dehart, C.V. Parks, Recommendations for Addressing Axial Burnup in PWR Burnup Credit Analyses (Oak Ridge National Laboratory, USA, 2003) NUREG/CR-6801 [Google Scholar]
- J.C Neuber, Evaluation of axial and horizontal burnup profiles, In: Technical committee meeting on implementation of burnup credit in spent fuel management systems, Vienna Austria, 10-14, IAEA-TECDOC-1241 (2001). https://www.osti.gov/etdeweb/servlets/purl/20198203. [Google Scholar]
- K. Kim, J. Hong, Criticality effect according to axial burnup profiles in PWR burnup credit analysis, Nucl. Eng. Technol. 51, 1708 (2019). https://www.sciencedirect.com/science/article/pii/S1738573319301421 [CrossRef] [Google Scholar]
- R.F Cacciapouti, S.V. Volkinburg, Update on the PWR axial burnup profile database, In: Proceedings of 6th annual international conference on high level radioactive waste management, 30 Apr - 5 May. Las Vegas, NV, United States (1995), p. 541 [Google Scholar]
- J.M Scaglione, PWR Axial Burnup Profile Analysis (Oak Ridge National Laboratory, NCAL-DSU-NU-000012 REV 00A; 2003) [Google Scholar]
- S. Caruso, Estimation of the radionuclide inventory in LWR spent fuel assembly structural materials for long-term safety analysis, EPJ Nucl. Sci. Technol. 2, 4 (2016). https://doi.org/10.1051/epjn/e2015-50057-8 [CrossRef] [EDP Sciences] [Google Scholar]
- M. Kromar, A.T. Godfrey, Determination of the spent fuel decay heat with the VERA core simulator, Front. Energy Res. 10, 1046506 (2022). https://www.frontiersin.org/articles/10.3389/fenrg.2022.1046506. [CrossRef] [Google Scholar]
- B. Ebiwonjumi, C. Kong, P. Zhang, A. Cherezov, D. Lee, Uncertainty quantification of PWR spent fuel due to nuclear data and modeling parameters, Nucl. Eng. Technol. 53, 715 (2021). https://www.sciencedirect.com/science/article/pii/S1738573320303521 [CrossRef] [Google Scholar]
- M. Kromar, B. Kurincic, Determination of the NPP Krsko spent fuel decay heat, In: AIP Conf. Proc. 21 July (2017), Vol. 1866 p. 050005. https://doi.org/10.1063/1.4994529 [CrossRef] [Google Scholar]
- D. Kotlyar, E. Shwageraus, On the use of predictor-corrector method for coupled Monte Carlo burnup codes, Ann. Nucl. Energy 58, 228 (2013). https://www.sciencedirect.com/science/article/pii/S0306454913001643 [CrossRef] [Google Scholar]
- J. Dufek, J.E. Hoogenboom, Numerical stability of existing Monte Carlo burnup codes in cycle calculations of critical reactors, Nucl. Sci. Eng. 162, 307 (2009) [CrossRef] [Google Scholar]
- J. Dufek, D. Kotlyar, E. Shwageraus, The stochastic implicit Euler method - A stable coupling scheme for Monte Carlo burnup calculations, Ann. Nucl. Energy 60, 295 (2013). https://www.sciencedirect.com/science/article/pii/S0306454913002703 [CrossRef] [Google Scholar]
- L. Fiorito, A. Stankovskiy, G. Van den Eynde, P.E. Labeau, Development of time-dependent reaction rates to optimise predictor-corrector algorithm in ALEPH burn-up code, Ann. Nucl. Energy 62, 307 (2013). https://www.sciencedirect.com/science/article/pii/S0306454913003113 [CrossRef] [Google Scholar]
- A.E Isotalo, P.A. Aarnio, Higher order methods for burnup calculations with Bateman solutions, Ann. Nucl. Energy 38, 1987 (2011). https://www.sciencedirect.com/science/article/pii/S0306454911001708 [CrossRef] [Google Scholar]
- A.E Isotalo, P.A. Aarnio, Substep methods for burnup calculations with Bateman solutions, Ann. Nucl. Energy 38, 2509 (2011). https://www.sciencedirect.com/science/article/pii/S0306454911002726 [CrossRef] [Google Scholar]
- J. Dufek, V. Valtavirta, Time step length versus efficiency of Monte Carlo burnup calculations, Ann. Nucl. Energy 72, 409 (2014). https://www.sciencedirect.com/science/article/pii/S0306454914002813 [CrossRef] [Google Scholar]
- J. Dufek, I. Mickus, Optimal time step length and statistics in Monte Carlo burnup simulations, Ann. Nucl. Energy 139 107244 (2020). https://www.sciencedirect.com/science/article/pii/S0306454919307546 [CrossRef] [Google Scholar]
- S.W.D. Hart, G. Maldonado-Ivan, S. Goluoglu, Implementation of the doppler broadening rejection correction in KENO, Trans. Am. Nucl. Soc. 36, 423 (2013) [Google Scholar]
- B. Becker, R. Dagan, G. Lohnert, Proof and implementation of the stochastic formula for ideal gas, energy dependent scattering kernel, Ann. Nucl. Energy 36, 470 (2009). https://www.sciencedirect.com/science/article/pii/S0306454908003186 [CrossRef] [Google Scholar]
- R. Dagan, C.H.M. Broeders, On the effect of resonance dependent scattering-kernel on fuel cycle and inventory, In: Proceedings of the PHYSOR 2006, Sept. 10-14. Vancouver, BC, Canada (2006) [Google Scholar]
- R. Dagan, On the use of S(αβ) tables for nuclides with well pronounced resonances, Ann. Nucl. Energy 32, 367 (2005). https://www.sciencedirect.com/science/article/pii/S0306454904002191 [CrossRef] [Google Scholar]
- R. Dagan, On the angular distribution of the ideal gas scattering kernel, Ann. Nucl. Energy 35, 1109 (2008). https://www.sciencedirect.com/science/article/pii/S0306454907002800 [CrossRef] [Google Scholar]
- W. Rothenstein, R. Dagan, Ideal gas scattering kernel for energy dependent cross-sections, Ann. Nucl. Energy 25, 209 (1998). https://www.sciencedirect.com/science/article/pii/S0306454997000637 [CrossRef] [Google Scholar]
- F.B Brown, Doppler Broadening Resonance Correction for Free-gas Scattering in MCNP6.2 (Los Alamos National Laboratory, 2019) LA-UR-19-24824 [Google Scholar]
- W.A Wieselquist, E.R.A. Lefebvre, SCALE Code System - Version 6.2.4 (Oak Ridge National Laboratory, ORNL/TM-SCALE-6.3.1, 2023) [Google Scholar]
- J. Leppänen, M. Pusa, T. Viitanen, V. Valtavirta, T. Kaltiaisenaho, The Serpent Monte Carlo code: Status, development and applications in 2013, Ann. Nucl. Energy 82, 142 (2015). https://www.sciencedirect.com/science/article/pii/S0306454914004095 [CrossRef] [Google Scholar]
- A.L Nichols, Nuclear Data Requirements for Decay Heat Calculations, in ICTP Lecture Notes 20, Workshop on Nuclear Reaction Data and Nuclear Reactors: Physics, Design and Safety, 25 February-28 March 2002, edited by M. Herman, N. Paver (ICTP Publication & Printing, Trieste, 2005), pp. 65–195, ISBN 92-95003-30-6 [Google Scholar]
- T. Yoshida, N. Hagura, R. Umezu, A. Algora, J.L. Tain, D. Jordan, et al., Impact of TAGS Measurement on FP Decay Data and Decay Heat Calculations, J. Korean Phys. Soc. 59, 1543 (2011). https://www.jkps.or.kr/journal/view.html?volume=59&number=2(3)&spage=1543&year=2011 [CrossRef] [Google Scholar]
- M. Fleming, J.C. Sublet, Validation of FISPACT-II, Decay Heat and Inventory, Predictions for Fission Events (Culham Centre for Fusion Energy, CCFE, UK, 2015) CCFE-R(15)28 [Google Scholar]
- A.L Nichols, P. Dimitriou, A. Algora, M. Fallot, L. Giot, F.G. Kondev, et al., Improving Fission-product Decay Data for Reactor Applications: Part I - Decay Heat, Eur. Phys. J. A 59, 78 (2023). https://hal.science/hal-03930912 [CrossRef] [Google Scholar]
- J.C Hardy, L.C. Carraz, B. Jonson, P.J. Hansen, The essential decay of pandemonium: A demonstration of errors in complex beta-decay schemes, Phys. Lett. B. 71, 307 (1977). https://www.sciencedirect.com/science/article/pii/0370269377902234 [CrossRef] [Google Scholar]
- J.L. Taìn, Beta-decay total absorption measurements for nuclear technology and astrophysics, In: International Conference on Nuclear Data for Science and Technology 2007, April 22-April 27. Nice, France (2008) [Google Scholar]
- R.C Greenwood, R.G. Helmer, M.H. Putnam, K.D. Watts, Measurement of β-decay intensity distributions of several fission-product isotopes using a total absorption γ-ray spectrometer, Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equipment 390, 95 (1997). https://www.sciencedirect.com/science/article/pii/S0168900297003562 [CrossRef] [Google Scholar]
- M.A Kellett, O. Bersillon, The Decay Data Evaluation Project (DDEP) and the JEFF-3.3 radioactive decay data library: Combining international collaborative efforts on evaluated decay data, EPJ Web Conf. 146, 02009 (2017). https://doi.org/10.1051/epjconf/201714602009 [Google Scholar]
- D. Cano-Ott, J.L. Tain, A. Gadea, B. Rubio, L. Batist, M. Karny, et al., Monte Carlo simulation of the response of a large NaI(Tl) total absorption spectrometer for β-decay studies, Nucl. Instrum. Methods Phys. Res. Sect. A Accelerators Spectrometers Detect. Assoc. Equipment 430, 333 (1999). https://www.sciencedirect.com/science/article/pii/S016890029900217X [CrossRef] [Google Scholar]
- D. Cano-Ott, J.L. Tain, A. Gadea, B. Rubio, L. Batist, M. Karny, et al., Pulse pileup correction of large NaI(Tl) total absorption spectra using the true pulse shape, Nucl. Instrum. Methods Phys. Res. Sect. A Accelerators Spectrometers Detect Assoc Equipment 430, 488 (1999). https://www.sciencedirect.com/science/article/pii/S0168900299002168 [CrossRef] [Google Scholar]
- J.L Tain, D. Cano-Ott, The influence of the unknown de-excitation pattern in the analysis of β-decay total absorption spectra, Nucl. Instrum. Methods Phys. Res. A. 571, 719 (2007) [CrossRef] [Google Scholar]
- J.L Tain, D. Cano-Ott, Algorithms for the analysis of β-decay total absorption spectra, Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equipment. 571, 728 (2007). https://www.sciencedirect.com/science/article/pii/S0168900206018985 [CrossRef] [Google Scholar]
- D. Paraskevi, Development of a reference database for beta-delayed neutron emission (International Atomic Energy Agency, 2015), INDC(NDS)-0683 [Google Scholar]
- M. Gupta, M.A. Kellett, A.L. Nichols, O. Bersillon, Decay Heat Calculations: Assessment of Fission Product Decay Data Requirements for Th/U Fuel (International Atomic Energy Agency, 2010) INDC(NDS)-0577 [Google Scholar]
- A.L Nichols, C. Nordborg, Total Absorption Gamma-ray Spectroscopy (TAGS), Current Status of Measurement Programmes for Decay Heat Calculations and Other Applications (International Atomic Energy Agency, 2009), INDC(NDS)-0551 [Google Scholar]
- A. Algora, D. Jordan, J.L. Taín, B. Rubio, J. Agramunt, A.B. Perez-Cerdan, et al., Reactor Decay Heat in 239Pu: Solving the γ Discrepancy in the 4-3000-s Cooling Period. Phys. Rev. Lett. 105, 202501 (2010). https://link.aps.org/doi/10.1103/PhysRevLett.105.202501 [CrossRef] [PubMed] [Google Scholar]
- D. Jordan, A. Algora, J.L. Tain, B. Rubio, J. Agramunt, A.B. Perez-Cerdan, et al., Total absorption study of the β decay of 102,104,105TC. Phys. Rev. C 87, 044318 (2013). https://link.aps.org/doi/10.1103/PhysRevC.87.044318 [CrossRef] [Google Scholar]
- A.A. Zakari-Issoufou, M. Fallot, A. Porta, A. Algora, J.L. Tain, E. Valencia, et al., Total Absorption Spectroscopy Study of 92Rb Decay: A Major Contributor to Reactor Antineutrino Spectrum Shape, Phys. Rev. Lett. 115, 102503 (2015). https://link.aps.org/doi/10.1103/PhysRevLett.115.102503 [CrossRef] [PubMed] [Google Scholar]
- S. Rice, A. Algora, J.L. Tain, E. Valencia, J. Agramunt, B. Rubio, et al., Total absorption spectroscopy study of the β decay of 86Br and 91Rb, Phys. Rev. C. 96, 014320 (2017). https://link.aps.org/doi/10.1103/PhysRevC.96.014320 [CrossRef] [Google Scholar]
- E. Valencia, J.L. Tain, A. Algora, J. Agramunt, E. Estevez, M.D. Jordan, et al., Total absorption γ-ray spectroscopy of the β-delayed neutron emitters 87Br, 88Br, and 94Rb, Phys. Rev. C 95, 024320 (2017). https://link.aps.org/doi/10.1103/PhysRevC.95.024320 [CrossRef] [Google Scholar]
- V. Guadilla, A. Algora, J.L. Tain, M. Estienne, M. Fallot, A.A. Sonzogni, et al., Large Impact of the Decay of Niobium Isomers on the Reactor ν̅e Summation Calculations. Phys. Rev. Lett. 122, 042502 (2019). https://link.aps.org/doi/10.1103/PhysRevLett.122.042502 [CrossRef] [Google Scholar]
- V. Guadilla, J.L. Tain, A. Algora, J. Agramunt, D. Jordan, M. Monserrate, et al., Total absorption γ-ray spectroscopy of the β-delayed neutron emitters 137I and 95Rb, Phys. Rev. C 100, 044305 (2019). https://link.aps.org/doi/10.1103/PhysRevC.100.044305 [CrossRef] [Google Scholar]
- V. Guadilla, L. Le Meur, M. Fallot, J.A. Briz, M. Estienne, L. Giot, et al., Total absorption γ-ray spectroscopy of the β decays of 96gs,mY, Phys. Rev. C. 106, 014306 (2022). https://link.aps.org/doi/10.1103/PhysRevC.106.014306 [CrossRef] [Google Scholar]
- B.C Rasco, M. Wolińska Cichocka, A. Fijałkowska, K.P. Rykaczewski, M. Karny, R.K. Grzywacz, et al., Decays of the Three Top Contributors to the Reactor ν̅e High-Energy Spectrum, 92Rb, 96gs,mY, and 142Cs, Studied with Total Absorption Spectroscopy, Phys. Rev. Lett. 117, 092501 (2016). https://link.aps.org/doi/10.1103/PhysRevLett.117.092501 [CrossRef] [Google Scholar]
- A. Fijałkowska, M. Karny, K.P. Rykaczewski, B.C. Rasco, R. Grzywacz, C.J. Gross, et al., Impact of Modular Total Absorption Spectrometer measurements of β decay of fission products on the decay heat and reactor ν̅e flux calculation, Phys. Rev. Lett. 119, 052503 (2017). https://link.aps.org/doi/10.1103/PhysRevLett.119.052503 [CrossRef] [Google Scholar]
- B.C Rasco, K.P. Rykaczewski, A. Fijałkowska, M. Karny, M. Wolińska Cichocka, R.K. Grzywacz, et al, Complete β-decay pattern for the high-priority decay-heat isotopes 137I and 137Xe determined using total absorption spectroscopy, Phys. Rev. C 95, 054328 (2017). https://link.aps.org/doi/10.1103/PhysRevC.95.054328 [CrossRef] [Google Scholar]
- A.L Nichols, P. Dimitriou, A. Algora, M. Fallot, L. Giot, F.G. Kondev, et al. Improving Fission-product Decay Data for Reactor Applications: Part I - Decay Heat, ArXiv e-prints [arXiv: 2212.10335] (2022). https://arxiv.org/abs/2212.10335 [Google Scholar]
- D.A Brown, M.B. Chadwick, R. Capote, A.C. Kahler, A. Trkov, MW Herman, et al., ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data, Nucl. Data Sheets 148, 1 (2018), Special Issue on Nuclear Reaction Data. https://www.sciencedirect.com/science/article/pii/S0090375218300206 [CrossRef] [Google Scholar]
- O. Iwamoto, N. Iwamoto, S. Kunieda, F. Minato, S. Nakayama, Y. Abe, et al. Japanese evaluated nuclear data library version 5: JENDL-5, J. Nucl. Sci. Technol. 60, 1 (2023). https://doi.org/10.1080/00223131.2022.2141903 [CrossRef] [Google Scholar]
- C. Moler, C. Van Loan, Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later, SIAM Rev. 45, 3 (2003). https://doi.org/10.1137/S00361445024180 [NASA ADS] [CrossRef] [Google Scholar]
- A.E Isotalo, P.A. Aarnio, Comparison of depletion algorithms for large systems of nuclides, Ann. Nucl. Energy 38, 261 (2011). https://www.sciencedirect.com/science/article/pii/S0306454910003889 [CrossRef] [Google Scholar]
- J. Cetnar, General solution of Bateman equations for nuclear transmutations, Ann. Nucl. Energy 33, 640 (2006). https://www.sciencedirect.com/science/article/pii/S0306454906000284 [CrossRef] [Google Scholar]
- J. Cetnar, P. Gronek, BISON-C: A one-dimensional transport and burnup calculation code with consideration of actinides and fission products, Nucl. Sci. Eng. 134, 236(2000) [Google Scholar]
- O. Kum, Development of easy-to-use interface for nuclear transmutation computing, VCINDER code, Nucl. Eng. Technol. 50, 25 (2018). https://www.sciencedirect.com/science/article/pii/S1738573316303370 [CrossRef] [Google Scholar]
- J. Cetnar, J. Wallenius, W. Gudowski, MCB. A continuous energy Monte Carlo burnup simulation code, In: Proceedings of the Actinide and fission product partitioning and transmutation, Nov. 25-27. Mol, Belgium: Nuclear Energy Agency of the OECD (NEA) (1998), pp. 523–527. https://oecd-nea.org/trw/docs/mol98/postersession/POSTSpaper12.pdf [Google Scholar]
- M. Oettingen, P. Stanisz, J. Cetnar, G. Kepisty, Transmutation trajectory analysis in the modelling of LFR fuel cycle, In: Proceedings of the International conference on fast reactors and related fuel cycles: next generation nuclear systems for sustainable development, June 26-29. Yekaterinburg, Russian Federation: International Atomic Energy Agency (IAEA) (2017), p. 26. https://inis.iaea.org/search/search.aspx?orig_q=RN:48087785 [Google Scholar]
- A.G Croff, ORIGEN2: A Versatile Computer Code for Calculating the Nuclide Compositions and Characteristics of Nuclear Materials, Nucl. Technol. 62, 335 (1983). https://doi.org/10.13182/NT83-1 [CrossRef] [Google Scholar]
- B.T Rearden, M.A. Jessee, SCALE Code System (Oak Ridge National Laboratory, USA, 2018) ORNL/TM-2005/39. https://www.ornl.gov/sites/default/files/SCALE_6.2.3.pdf [Google Scholar]
- D.I Poston, H.R. Trellue, User’s manual, version 1.00 for Monteburns, version 3.01 (Los Alamos National Laboratory, USA, 1998) LA-UR-98-2718 [Google Scholar]
- R.S Babcock, R.L. Moore, D.E. Wessol, B.G. Schnitzler, C.A. Wemple, MOCUP: MCNP=ORIGEN2 Coupling Utility Programs, In: Proceedings of the 4th meeting of the International Group On Research Reactors, IGORR-IV, May 24-25. Gatlinburg, TN, USA (1995). https://www.igorr.com/Documents/1995-GATLINBURG/36023816.pdf [Google Scholar]
- J. Sanz, O. Cabellos, N. García-Herranz, ACAB Inventory code for nuclear applications: User’s manual V. 2008, NEA-1839 6, 475 (2008) [Google Scholar]
- A. Talamo, F. Álvarez-Velarde, E.M. González-Romero, A Fast Numerical Method for the Calculation of the Equilibrium Isotopic Composition of a Transmutation System in an Advanced Fuel Cycle. Sci. Technol. Nuc. Instal. 2012, 149089 (2012). https://doi.org/10.1155/2012/149089 [Google Scholar]
- W. Haeck, B. Cochet, L. Aguiar, Monte Carlo depletion calculations using VESTA 2.1 new features and perspectives, In: International Conference on the Physics of Reactors 2012, PHYSOR 2012: Advances in Reactor Physics (2012), Vol. 3 [Google Scholar]
- E. Hairer, G. Wanner, Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems (Springer Series in Comput. Mathematics, Springer-Verlag, 1996), Vol. 14, p. 1991 [Google Scholar]
- R.B Sidje, Expokit: A Software Package for Computing Matrix Exponentials, ACM Trans. Math. Softw. 24, 130 (1998). https://doi.org/10.1145/285861.285868 [CrossRef] [Google Scholar]
- A. Stankovskiy, G. Van Den Eynde, P. Baeten, C. Trakas, P.M. Demy, L. Villatte, ALEPH2 - A general purpose Monte Carlo depletion code, In: Proceedings of the PHYSOR 2012: Conference on Advances in Reactor Physics - Linking Research, Industry, and Education, April 15-20. Knoxville, Tennessee, USA (2012) [Google Scholar]
- M.A Bochev, A short guide to exponential Krylov subspace time integration for Maxwell’s equations, No. 1992 in Memorandum (University of Twente, Department of Applied Mathematics, 2012) [Google Scholar]
- M. Pusa, Higher-Order Chebyshev Rational Approximation Method and Application to Burnup Equations, Nucl. Sci. Eng. 182, 297 (2016). https://doi.org/10.13182/NSE15-26 [CrossRef] [Google Scholar]
- NEA/WPNCS/EGADSNF, Evaluation guide for the Evaluated Spent Nuclear Fuel Assay Database (SFCOMPO) (Nuclear Energy Agency, NEA/NSC/R(2015)8, 2015). https://www.oecd-nea.org/jcms/pl_19678 [Google Scholar]
- A. Shama, D. Rochman, S. Pudollek, S. Caruso, A. Pautz, Uncertainty analyses of spent nuclear fuel decay heat calculations using SCALE modules, Nucl. Eng. Technol. 53, 2816 (2021). https://www.sciencedirect.com/science/article/pii/S1738573321001558 [CrossRef] [Google Scholar]
- D. Rochman, A. Vasiliev, H. Ferroukhi, M. Hursin, Analysis for the ARIANE BM1 and BM3 samples: nuclide inventory and decay heat, EPJ Nucl. Sci Technol. 7, 18 (2021). https://doi.org/10.1051/epjn/2021017 [CrossRef] [EDP Sciences] [Google Scholar]
- R. Macian, M.A. Zimmermann, R. Chawla, Statistical Uncertainty Analysis Applied to Fuel Depletion Calculations, J. Nucl. Sci. Technol. 44, 875 (2007). https://www.tandfonline.com/doi/abs/10.1080/18811248.2007.9711325 [CrossRef] [Google Scholar]
- A. Hernandez-Solis, Uncertainty and sensitivity analysis applied to LWR neutronic and thermalhydraulic calculations (Chalmers University of Technology, Goteborg, Sweden, 2012) [Google Scholar]
- W. Wulff, B.E. Boyack, I. Catton, R.B. Duffey, P. Griffith, K.R. Katsma, et al. Quantifying reactor safety margins part 3: Assessment and ranging of parameters, Nucl. Eng. Design 119, 33 (1990). https://www.sciencedirect.com/science/article/pii/0029549390900737 [CrossRef] [Google Scholar]
- R.N Bratton, M. Avramova, K. Ivanov, OECD/NEA Benchmark for uncertainty analysis in modeling (UAM) for LWRs - summary and discussion of neutronics cases (Phase I), Nucl. Eng. Technol. 46, 313 (2014). https://www.sciencedirect.com/science/article/pii/S1738573315301285 [CrossRef] [Google Scholar]
- E. Canuti, A. Petruzzi, F. D’Auria, T. Kozlowski, Sensitivity Studies for the Exercise I-1 of the OECD/UAM Benchmark, Sci. Technol. Nucl. Install. 2012, 817185 (2012). https://doi.org/10.1155/2012/817185 [CrossRef] [Google Scholar]
- L. Caillot, C. Nonon, V. Basini, Out-of-pile and in-pile viscoplastic behaviour of mixed-oxide fuels, In: Pellet-clad Interaction in Water Reactor Fuels, 9-11 March. Aix-en-Provence, France (2004), p. 153. https://www.oecd-nea.org/upload/docs/application/pdf/2019-12/6004-pellet-clad.pdf [Google Scholar]
- A.V Smirnov, B.A. Kanashov, D.V. Markov, V.A. Ovchinikov, V.S. Polenok, A.A. Ivashchenko, Pellet-cladding interaction in VVER fuel rods, In: Pellet-clad Interaction in Water Reactor Fuels, 9-11 March. Aix-en-Provence, France (2004), p. 231. https://www.oecd-nea.org/upload/docs/application/pdf/2019-12/6004-pellet-clad.pdf [Google Scholar]
- C. Mougel, B. Verhaeghe, C. Verdeau, S. Lansiart, S. Béguin, B. Julien, Power ramping in the OSIRIS reactor: database analysis for standard UO2 fuel with ZY-4 cladding. In: Pellet-clad Interaction in Water Reactor Fuels, 9-11 March. Aix-en-Provence, France (2004), p. 333. https://www.oecd-nea.org/upload/docs/application/pdf/2019-12/6004-pellet-clad.pdf [Google Scholar]
- C. Garnier, P. Mailhe, P. Vesco, L.C. Bernard, C. Delafoy, P. Garcia, The COPERNIC mechanical model and its application to doped fuel, In: Pellet-clad Interaction in Water Reactor Fuels, 9-11 March. Aix-en-Provence, France (2004), p. 465. https://www.oecd-nea.org/upload/docs/application/pdf/2019-12/6004-pellet-clad.pdf [Google Scholar]
- R. Manzel, C.T. Walker, EPMA and SEM of fuel samples from PWR rods with an average burn-up of around 100 MWd/kgHM, J. Nucl. Mater. 301, 170 (2002). https://www.sciencedirect.com/science/article/pii/S002231150100753X [CrossRef] [Google Scholar]
- D. Rochman, A. Vasiliev, H. Ferroukhi, M. Hursin, Analysis for the ARIANE GU1 sample: Nuclide inventory and decay heat, Ann. Nucl. Energy 160, 108359 (2021). https://www.sciencedirect.com/science/article/pii/S0306454921002358 [CrossRef] [Google Scholar]
- D. Rochman, A. Vasiliev, H. Ferroukhi, A.M. Noz, M.V. Antolin, M.B. Torres, et al. Analysis of ENRESA BWR samples: nuclide inventory and decay heat, EPJ Nucl. Sci. Technol. 8, 9 (2022). https://doi.org/10.1051/epjn/2022007 [CrossRef] [EDP Sciences] [Google Scholar]
- Y. Kovbasenko, Comparative Analysis of VVER-1000 Westinghouse and TVEL Spent Fuel Capability, Univ. J. Phys. Appl. 10, 105 (2016) [Google Scholar]
- J. Vojackova, F. Novotny, K. Katovsky, Safety analyses of reactor VVER 1000, Energy Procedia 127, 352 (2017) [CrossRef] [Google Scholar]
- I. Christoskov, L. Tsankov, N. Ivanov, The feasibility of express in situ measurement of the isotopic composition of uranium in fresh WWER-1000 fuel, In: Proceedings of the 9 International conference on WWER fuel performance, modelling and experimental support (Bulgarian Academy of Sciences, Sofia, Bulgaria, 2011), pp. 879–888 [Google Scholar]
- D.V Hristov, P.V. Petkov, I. Naev, Calculation of decay heat rate in VVER-1000 spent fuel pool including uncertainties, Nucl. Eng. Design 366, 110754 (2020) [CrossRef] [Google Scholar]
- C. Frepoli, H. Glaeser, GRS Method for Uncertainty and Sensitivity Evaluation of Code Results and Applications, Sci. Technol. Nucl. Install. 798901-7 (2008). https://doi.org/10.1155/2008/798901 [Google Scholar]
- M. Kloos, Mean features of the tool SUSA 4.0 for uncertainty and sensitivity analyses, In: Safety and Reliability of Complex Engineered Systems, edited by L. Podofillini, B. Sudret, B. Stojadinovic, E. Zio, W. Kröger (CRC Press, London, UK, 2015), pp. 107–132 [Google Scholar]
- S.S Wilks, Determination of Sample Sizes for Setting Tolerance Limits, Ann. Math. Stat. 12, 91 (1941) [CrossRef] [Google Scholar]
- S.S Wilks, Statistical Prediction with Special Reference to the Problem of Tolerance Limits, Ann. Math. Stat. 13, 400 (1942). https://doi.org/10.1214/aoms/1177731537 [CrossRef] [Google Scholar]
- IAEA. Storage of Spent Nuclear Fuel, No. SSG-15 in Specific Safety Guides (International Atomic Energy Agency, Vienna, 2012). https://www.iaea.org/publications/8532/storage-of-spent-nuclear-fuel [Google Scholar]
- A. Tsilanizara, T.D. Huynh, New feature of DARWIN/PEPIN2 inventory code: Propagation of nuclear data uncertainties to decay heat and nuclide density, Ann. Nucl. Energy 164, 108579 (2021) [CrossRef] [Google Scholar]
- H. Golfier, R. Lenain, J.J. Lautard, P. Fougeras, P. Magat, E. Martinolli, et al, APOLLO3: a common project of CEA, AREVA and EDF for the development of new deterministic multi-purpose code for core physics analysis, In: International Conference on Mathematics, Computational Methods Reactor Physics (Saratoga Springs, New-York, 2009) [Google Scholar]
- M. Coste-Delclaux, GALILÉE: A nuclear data processing system for transport, depletion and shielding codes, In: Proc. Int. Conf. PHYSOR 2008, Interlaken, Switzerland, 14-19 September, 2008 (2008) [Google Scholar]
- S. Lahaye, P. Bellier, H. Mao, A. Tsilanizara, Y. Kawamoto, First verification and validation steps of MENDEL release 1.0 cycle code system, In: Proc. Int. Conf. PHYSOR2014, Kyoto, Japan, Sept. 28 - Oct 3 (2014) [Google Scholar]
- E. Brun et al, Tripoli-4, CEA, EDF and AREVA reference Monte Carlo code, In: SNA+ MC 2013-Joint International Conference on Supercomputing in Nuclear Applications+ Monte Carlo (2014), p. 06023 [Google Scholar]
- S. Lahaye, A. Tsilanizara, P. Bellier, T. Bittar, Implementation of a CRAM solver in MENDEL Depletion Code System, In: International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering (2017) [Google Scholar]
- F. Gaudier, URANIE : The CEA/DEN Uncertainty and Sensitivity platform, In: Procedia - Social and Behavioral Sciences (2010), Vol. 2 [Google Scholar]
- J.B Blanchard, G. Damblin, J.M. Martinez, G. Arnaud, F. Gaudier, The Uranie platform: an open-source software for optimisation, meta-modelling and uncertainty analysis, EPJ Nucl. Sci. Technol. 5, 4 (2019) [CrossRef] [EDP Sciences] [Google Scholar]
- S. Lahaye, J. Luo, P. Bellier, T.D. Huynh, A. Tsilanizara, Uncertainty quantification of isotopic densities in depleted fuel, In: ANS Best Estimate Plus Uncertainty International Conference (BEPU, 2018) [Google Scholar]
- M.J Bell, The ORNL Isotope Generation and Depletion Code. Union Carbide Corporation (Nuclear Division) (Oak Ridge National Laboratory, USA, 1973), ORNL-4628 [Google Scholar]
- I.C Gauld, G. Radulescu, G. Ilas, B.D. Murphy, M.L. Williams, D. Wiarda, Isotopic depletion and decay methods and analysis capabilities in SCALE, Nucl. Technol. 174, 169 (2011). https://doi.org/10.13182/NT11-3 [CrossRef] [Google Scholar]
- M.D DeHart, S.M. Bowman, Reactor Physics Methods and Analysis Capabilities in SCALE, Nucl. Technol. 174, 196 (2011). https://doi.org/10.13182/NT174-196 [CrossRef] [Google Scholar]
- M.A Jessee, W.A. Wieselquist, U. Mertyurek, K.S. Kim, T.M. Evans, S.P. Hamilton, et al. Lattice physics calculations using the embedded self-shielding method in Polaris, Part I: Methods and implementation, Ann. Nucl. Energy 150, 107830 (2021). https://www.sciencedirect.com/science/article/pii/S0306454920305284 [CrossRef] [Google Scholar]
- G. Ilas, J.R. Burns, B.D. Hiscox, U. Mertyurek, SCALE 6.2.4 Validation: Reactor Physics (Oak Ridge National Laboratory, 2022) ORNL/TM-2020/1500/v3. https://info.ornl.gov/sites/publications/Files/Pub138919.pdf [Google Scholar]
- J. Rhodes, K. Smith, D. Lee, CASMO-5 Development and Applications. In: Proceedings of the PHYSOR 2006, Sept. 10-14. Vancouver, BC, Canada (2006), p. B144. https://www.studsvik.com/SharepointFiles/CASMO-5%20Development%20and%20Applications.pdf [Google Scholar]
- T. Bahadir, S.O. Lindhal, Studsvik’s Next Generation Nodal Code SIMULATE-5, In: Proceedings of the conference on Advances in Nuclear Fuel Management IV (ANFM IV), April 12-15. Hilton Head, SC, USA (2009) [Google Scholar]
- S. Børresen, Spent Fuel Analyses based on In-Core Fuel Management Calculations, In: Proceedings of the PHYSOR 2004, April 25-29 (Chicago, Illinois, USA, 2004) [Google Scholar]
- T. Simeonov, C. Wemple, Development in Studsvik’s system for spent fuel analyses, In: Proceedings of the 26th AER symposium, Oct. 10-14. Helsinki, Finland (2016) [Google Scholar]
- M.B Chadwick, M. Herman, P. Obložinský, M.E. Dunn, Y. Danon, A.C. Kahler, et al. ENDF/B-VII.1 Nuclear Data for Science and Technology: Cross Sections, Covariances, Fission Product Yields and Decay Data, Nucl. Data Sheets 112, 2887 (2011), Special Issue on ENDF/B-VII.1 Library. https://www.sciencedirect.com/science/article/pii/S009037521100113X [CrossRef] [Google Scholar]
- R. Ferrer, J. Rhodes, Generation and initial validation of a new CASMO5 ENDF/B-VIII.0 nuclear data library. In: Proceedings of the PHYSOR 2020, March 29-April 2. Cambridge, UK (2020) [Google Scholar]
- R.J.J. Stammler, M.J. Abbate, Methods of Steady-State Reactor Physics in Nuclear Design (IAcademic Press, UK, 1983) [Google Scholar]
- J.K Tuli, Evaluated Nuclear Structure Data File (Brookhaven National Laboratory, NBNL-NCS-51655-01/02-Rev, 2001) [Google Scholar]
- A.J Koning, D. Rochman, J.C. Sublet, N. Dzysiuk, M. Fleming, S. van der Marck, TENDL: Complete Nuclear Data Library for Innovative Nuclear Science and Technology, Nucl. Data Sheets 155, 1 (2019), Special Issue on Nuclear Reaction Data. https://www.sciencedirect.com/science/article/pii/S009037521930002X [CrossRef] [Google Scholar]
- A.J Koning, D. Rochman, Modern Nuclear Data Evaluation with the TALYS Code System, Nucl. Data Sheets 113, 2841 (2012), Special Issue on Nuclear Reaction Data. https://www.sciencedirect.com/science/article/pii/S0090375212000889 [NASA ADS] [CrossRef] [Google Scholar]
- M.J Berger, J.S. Coursey, M.A. Zucker, J. Chang, Stopping-Power & Range Tables for Electrons, Protons, and Helium Ions (NIST Standard Reference Database, 2015). https://www.nist.gov/pml/stopping-power-range-tables-electrons-protons-and-helium-ions [Google Scholar]
- T. Simeonov, C. Wemple, Update and evaluation of decay data for spent nuclear fuel analyses, EPJ Web Conf. 146, 09011 (2017). https://doi.org/10.1051/epjconf/201714609011 [CrossRef] [EDP Sciences] [Google Scholar]
- R.W Peele, F.C. Maienschein, The absolute spectrum of photons emitted in coincidence with thermal-neutron fission of Uranium-235 (Oak Ridge National Laboratory, 1970), ORNL-4457 [Google Scholar]
- A.C Kahler, The NJOY Nuclear Data Processing System, Version 2012, updated for NJOY2012.40 (Los Alamos National Laboratory, USA, 2014), LA-UR-12-27079 [Google Scholar]
- R.T Perry, W.B. Wilson, Neutron Production from (α,n) Reactions and Spontaneous Fission in ThO2, UO2, and (U,Pu)O2 Fuels (Los Alamos Scientific Laboratory, USA, 1981), LA-8869-MS [Google Scholar]
- M.G Stamatelatos, T.R. England, Accurate Approximations to Average Beta-Particle Energies and Spectra, Nucl. Sci. Eng. 63, 204 (1977). https://doi.org/10.13182/NSE77-A27028 [CrossRef] [Google Scholar]
- G.K Schenter, P. Vogel, A Simple Approximation of the Fermi Function in Nuclear Beta Decay, Nucl. Sci. Eng. 83, 393 (1983). https://doi.org/10.13182/NSE83-A17574 [CrossRef] [Google Scholar]
- R.F Burstall, FISPIN-A computer code for nuclide inventory calculations (UKAEA Risley Nuclear Power Development Establishment, 1979), ND-R-328 [Google Scholar]
- J. Sidell, EXTRA: A digital computer program for the solution of stiff sets of ordinary initial value, first order differential equations (UKAEA, 1976), AEEW-R-799 [Google Scholar]
- D. Parker, R. Mills, FISPIN10 validation review, BNFL Research and Development (BNFL, 2001), RAT 1972 Issue 2. https://www.oecd-nea.org/science/wpncs/ADSNF/reports/Magnox/FISPIN.pdf [Google Scholar]
- F. Alvarez-Velarde, E.M. Gonzàlez-Romero, I.M. Rodríguez, Validation of the burn-up code EVOLCODE 2.0 with PWR experimental data and with a Sensitivity/Uncertainty analysis, Ann. Nucl. Energy 73, 175 (2014). https://doi.org/10.1016/j.anucene.2014.06.049 [CrossRef] [Google Scholar]
- J. Sanz, O. Cabellos, N. Garcia-Herranz, ACAB-2008: Activation Abacus Code V2008 (NEA Data Bank, 2008) NEA-1839 [Google Scholar]
- A.G Croff, A User’s Manual for the ORIGEN2 Computer Code (1980) ORNL/TM-7175. [Google Scholar]
- J.L Conlin, F.B. Brown, A.C. Kahler, M.B. Lee, D.K. Parsons, M.C. White, Updating the Format of ACE Data Tables (Los Alamos National Laboratory, 2012), LA-UR-12-22033 [Google Scholar]
- W. Haeck, B. Decheneaux, VESTA User’s Manual - Version 2.2.0, IRSN, France, 2017, PSN-EXP/SNC/2017-00251 [Google Scholar]
- R. Ichou, B. Decheneaux, On the validation of VESTA 2.2.0 using the ARIANE-GU3 sample. EPJ Web Conf. 247 10005 (2021). https://doi.org/10.1051/epjconf/202124710005. [CrossRef] [EDP Sciences] [Google Scholar]
- J. Leppänen, M. Pusa, T. Viitanen, V. Valtavirta, T. Kaltiaisenaho, The Serpent Monte Carlo code: Status, development and applications in 2013, Ann. Nucl. Energy 82, 142 (2015). https://doi.org/10.1016/j.anucene.2014.08.024 [CrossRef] [Google Scholar]
- J. Leppänen, M. Pusa, E. Fridman, Overview of methodology for spatial homogenization in the Serpent 2 Monte Carlo code, Ann. Nucl. Energy 96, 126 (2016). https://doi.org/10.1016/j.anucene.2016.06.007 [CrossRef] [Google Scholar]
- J. Leppänen, V. Valtavirta, A. Rintala, V. Hovi, R. Tuominen, J. Peltonen, et al. Current Status and On-Going Development of VTT’s Kraken Core Physics Computational Framework. Energies 15, 876 (2022). https://doi.org/10.3390/en15030876 [CrossRef] [Google Scholar]
- J. Leppänen, Methodology, applications and performance of the CAD-based geometry type in the serpent 2 Monte Carlo code, Ann. Nucl. Energy 176, 109259 (2022). https://doi.org/10.1016/j.anucene.2022.109259 [CrossRef] [Google Scholar]
- M. Pusa, J. Leppänen, Computing the Matrix Exponential in Burnup Calculations, Nucl. Sci. Eng. 164, 140 (2010). https://doi.org/10.13182/NSE09-14 [CrossRef] [Google Scholar]
- K. Okumura, T. Mori, M. Nakagawa, K. Kaneko, Validation of a continuous-energy monte carlo burn-up code mvp-burn and its application to analysis of post irradiation experiment, J. Nucl. Sci. Technol. 37, 128 (2000) [CrossRef] [Google Scholar]
- T. Kashima, K. Suyama, T. Takada, SWAT4.0 - The Integrated Burnup Code System Driving Continuous Energy Monte Carlo Codes MVP, MCNP and Deterministic Calculation Code SRAC (Japan Atomic Energy Agency, 2015), JAEA-Data/Code 2014-028 [Google Scholar]
- Y. Nagaya, K. Okumura, K. Sakurai, T. Mori, MVP/GMVP Version 3 : General Purpose Monte Carlo Codes for Neutron and Photon Transport Calculations Based on Continuous Energy and Multigroup Methods (Japan Atomic Energy Agency, 2017), JAEA-Data/Code 2016-018 [Google Scholar]
- K. Okumura, T. Kugo, K. Kaneko, K. Tsuchihara, SRAC2006: A Comprehensive Neutronics Calculation Code System (Japan Atomic Energy Agency, 2007), JAEA-Data/Code 2007-004 [Google Scholar]
- K. Okumura, K. Sugino, K. Kojima, T. Jin, T. Okamoto, J. Katakura, A Set of ORIGEN2 cross section libraries based on JENDL-4.0; ORLIBJ40 (Japan Atomic Energy Agency, 2013), JAEA-Data/Code 2012-032 [Google Scholar]
- K. Tsubakihara, S. Okumura, C. Ishizuka, T. Yoshida, F. Minato, S. Chiba, Evaluation of fission product yields and associated covariance matrices, J. Nucl. Sci. Technol. 58, 151 (2021) [CrossRef] [Google Scholar]
- P. Dimitriou, I. Dillmann, B. Singh, V. Piksaikin, K.P. Rykaczewski, J.L. Tain, et al. Development of a Reference Database for Beta-Delayed Neutron Emission, Nucl. Data Sheets 173, 144 (2021), Special Issue on Nuclear Reaction Data. https://www.sciencedirect.com/science/article/pii/S0090375221000168 [CrossRef] [Google Scholar]
- K. Nishihara, H. Iwamoto, K. Suyama, Estimation of fuel compositions in Fukushima-Daiichi Nuclear Power Plant (Japan Atomic Energy Agency, JAEA-Data/Code 2012-018, 2012) [Google Scholar]
- M. Suzuki, A Development of Multi-Physics Burnup Analysis System (1) An Overall Plan and Implementation of Burnup Calculation Module. In: Proceedings of Annual Meeting of the Atomic Energy Society of Japan, 2021 March 17-19. [in Japanese] (2021) [Google Scholar]
- M. Suzuki, A development of Multi-Physics Burnup Analysis System (2) Implementation of Burnup Analysis Function with Fuel Assembly Geometry, In: Proceedings of Annual Meeting of the Atomic Energy Society of Japan, 2022 March 16-18, [in Japanese] (2022) [Google Scholar]
- M. Suzuki, S. Sato, A development of Multi-Physics Burnup Analysis System (3) Burnup Calculation Applying Exact Resonance Elastic Scattering model. In: Proceedings of Annual Meeting of the Atomic Energy Society of Japan, 2022 March 16-18, [in Japanese] (2022) [Google Scholar]
- M. Suzuki, K. Inagaki, S. Sato, S. Kitajima, A development of Multi-Physics Burnup Analysis System (4) Implementation of Thermal-Hydraulics Calculation Function. In: Proceedings of Fall Meeting of the Atomic Energy Society of Japan, 2022 September 7-9, [in Japanese] (2022) [Google Scholar]
- K. Okumura, K. Kojima, O. Okamoto, Development of the burn-up chain data ChainJ40 based on JENDL-4.0, In: Proceedings of Annual meeting of the Atomic Energy Society of Japan, 2012 Mar 19-21, [CD-ROM, in Japanese] (2012) [Google Scholar]
- T. Mori, Y. Nagaya, Comparison of Resonance Elastic Scattering Models Newly Implemented in MVP Continuous-Energy Monte Carlo Code, J Nucl. Sci. Technol. 46, 793(2009) [CrossRef] [Google Scholar]
- N. Garcia-Herranz, O. Cabellos, J. Sanz, Applicability of the MCNP-ACAB System to Inventory Prediction in High Burn-up Fuels: Sensitivity/Uncertainty Estimates. In: Proceedings of the International Conferecence on Mathematics and Computation, M&C2005 (Avignon, France, 2005) [Google Scholar]
- P. Ortego, C. Töre, A. Crespo, P. Mata, L. Garcia-Delgado, O. Cabellos, et al. Calculation with MCNP of Reactivity and Power Distribution of Atrium-10XP Design and Comparison with Isotopics Obtained with Monteburns, MCNP-ACAB and CASMO4, In: International Meeting on LWR Fuel Performance (Salamanca, Spain, 2006) [Google Scholar]
- N. Garcia-Herranz, O. Cabellos, J. Sanz, J. Juan, J.C. Kuijper, Propagation of statistical and nuclear data uncertainties in Monte Carlo burn-up calculations, Ann. Nucl. Energy 35, 714 (2008). https://www.sciencedirect.com/science/article/pii/S0306454907001958 [CrossRef] [Google Scholar]
- O. Cabellos, V. de Fusco, C.J. Diez de la Obra, J.S. Martinez, E. Gonzalez, D. Cano-Ott, et al. Testing JEFF-3.1.1 and ENDF/B-VII.1 Decay and Fission Yield Nuclear Data Libraries with Fission Pulse Neutron Emission and Decay Heat Experiments, Nucl. Data Sheets 118, 472 (2014). https://www.sciencedirect.com/science/article/pii/S0090375214001409 [CrossRef] [Google Scholar]
- ASN, IRSN, Qualification des outils de calcul scientifique utilisés dans la démonstration de sûreté nucléaire - première barrière (Autorité de Sûreté Nucléaire, France, 2017), Guide numéro 28. https://www.irsn.fr/sites/default/files/documents/expertise/demarches-de-surete/ASN_Guide-n28_Qualification-outils-calculs-scientifiques.pdf [Google Scholar]
- American Nuclear Society, Validation Of Neutron Transport Methods For Nuclear Criticality Safety, AANSI/ANS-8.24-2017 (R2023) (2017) [Google Scholar]
- International Organization for Standardization, Nuclear energy, nuclear technologies, and radiological protection Vocabulary Part 3: Nuclear fuel cycle (2015) [Google Scholar]
- For Nuclear Regulation Office, Validation of Computer Codes and Calculation Methods - Nuclear Safety Technical Assessment Guide. (Office for Nuclear Regulation, UK, 2019), NS-TAST-GD-042 Revision 5. https://www.onr.org.uk/operational/tech_asst_guides/ns-tast-gd-042.pdf [Google Scholar]
- A. Stankovskiy, G. Van den Eynde, T. Vidmar, Development and validation of ALEPH Monte Carlo burnup code, In: Proceedings of the International Workshop NEMEA-6, NEA/NSC/DOC(2011)4, 25-28 October (Krakow, Poland, 2010), pp. 161–169 [Google Scholar]
- L. Massinon, Validation of ALEPH2 depletion code on the spent fuel isotopic content of samples irradiated in Gösgen PWR core. Ecole polytechnique de Louvain (Louvain, Belgium, 2018), UCL 13305. http://hdl.handle.net/2078.1/thesis:13305 [Google Scholar]
- A. Stankovskiy, G. Van den Eynde, Validation of ALEPH2 code on the isotopic content of high burnup PWR samples from Vandellos-II reactor, SCK-CEN (2017), SCK-CEN-R-6291 and SCK-CEN/21547854 [Google Scholar]
- D. Gérard, Validation expérimentale du code ALEPH2 dévolution du combustible pour le calcul de chaleur résiduelle. Ecole polytechnique de Louvain (Louvain, Belgium, 2018), UCL 17217. http://hdl.handle.net/2078.1/thesis:17217 [Google Scholar]
- M. Broustaut, Benchmarking of the ALEPH Burn-Up code (SCK-CEN; 2012), SCK-CEN/36467063 [Google Scholar]
- D. Rochman, A. Vasiliev, H. Ferroukhi, M. Seidl, J. Basualdo, Improvement of PIE analysis with a full core simulation: The U1 case. Ann. Nucl. Energy 148, 107706 (2020). https://www.sciencedirect.com/science/article/pii/S0306454920304047 [CrossRef] [Google Scholar]
- T. Simeonov, C. Wemple, A procedure for verification of Studsvik’s spent nuclear fuel code SNF, Kerntechnik 84, 246 (2019). https://doi.org/10.3139/124.190005 [cited 2023-05-01] [Google Scholar]
- T. Simeonov, C. Wemple, Advances in Studsvik’s system for spent fuel analysis. EPJ Web Conf. 247, 02021 (2021). https://doi.org/10.1051/epjconf/202124702021 [CrossRef] [EDP Sciences] [Google Scholar]
- S. Tittelbach, T. Mispagel, P.W. Phlippen, Validation of SCALE/TRITON and HELIOS for prediction of isotopic inventories of high burnup LWR fuel, In: Advances in Nuclear Fuel Management IV (ANFM 2009) Hilton Head Island, South Carolina, USA, April 12-15, 2009, on CD-ROM (American Nuclear Society, LaGrange Park, IL, 2009) [Google Scholar]
- J.C Benoit, Decay heat of sodium fast reactor: Comparison of experimental measurements on the PHENIX reactor with calculations performed with the French DARWIN package, In: Proceedings of the PHYSOR 2012: Conference on Advances in Reactor Physics - Linking Research, Industry, and Education, April 15-20 (Knoxville, Tennessee, USA, 2012) [Google Scholar]
- H.A Knapp, Earings before the special subcommittee on radiation of the joint committee on atomic energy congress of the United States; 86th congress, first session, Fallout from Nuclear Weapons Tests (1959), Vol. 3 [Google Scholar]
- D.R Patterson, R.I. Schlitz, School of Nuclear Science and Engineering: The Determination of Heat Generation in Irradiated Uranium, Expt. No.11 (Argonne National Laboratory, 1955) [Google Scholar]
- M.M. El-Wakil, Nuclear Heat Transport (International Textbook Company, 1971) [Google Scholar]
- Y. Nauchi, S. Sato, A. Sasahara, A Numerical simulation on Bremsstrahlung Ray Measurement for β-Decay in Spent Nuclear Fuel. In: Proceedings of the 2021 Fall meeting of Atomic Energy Society of Japan (8-10 September, 2021) [Google Scholar]
- G. Ilas and J. Burns, SCALE 6.2.4 Validation for Light Water Reactor Decay Heat Analysis, Nucl. Technol. 208, 403 (2021) [Google Scholar]
Cite this article as: Dimitri Rochman, Alejandro Algora, Francisco Àlvarez-Velarde, Aurélie Bardelay, Øystein Bremnes, Oscar Cabellos, Daniel Cano-Ott, Luigi Capponi, Coralie Carmouze, Stefano Caruso, Andrew Cummings, Ron Dagan, Muriel Fallot, Luca Fiorito, Lydie Giot, Kevin Govers, Silja Häkkinen, Volker Hannstein, Axel Hoefer, Tan Dat Huynh, Raphaëlle Ichou, Germina Ilas, Pauli Juutilainen, Lukasz Koszuk, Marjan Kromar, Sébastien Lahaye, James Lam, Frédéric Laugier, Agnés Launay, Vincent Léger, David Lecarpentier, Jaakko Leppanen, Fadhel Malouch, Julie-Fiona Martin, David McGinnes, Robert William Mills, Futoshi Minato, Yasushi Nauchi, Pedro Ortego, Plamen Petkov, Pablo Romojaro, Shunsuke Sato, Marcus Seidl, Ahmed Shama, Teodosi Simeonov, Anders Sjöland, Virginie Solans, Fabian Sommer, Sven Tittelbach, Aimé Tsilanizara, Efstathios Vlassopoulos, Vanessa Vallet, Alexander Vasiliev, Tomoaki Watanabe, Gašper Žerovnik. An introduction to Spent Nuclear Fuel decay heat for, Light Water Reactors: a review from the NEA WPNCS, EPJ Nuclear Sci., Technol. 10, 9 (2024)
All Tables
Calculated over experimental ratios for LWR SNF assemblies (average and 1 standard deviation).
Example of single assembly burnup calculations for a UO2 and a MOX assembly. Both are initially enriched at 4% in fissile materials. Calculations are performed with CASMO5. “Fis.” corresponds to the fissile nuclides and “Fer.” to the fertile nuclides.
Heat generated by the most dominant nuclides (98.2% of the generated heat), 6 months after reactor shut down for a representative 55 MWd/kgHM burnup.
Summary of existing integral decay heat measurements using calorimetric methods.
Summary of existing decay heat measurements using calorimetric methods on LWR SNF assemblies.
Summary of existing differential decay heat measurements for neutron-induced fission on specific systems. Measurements are given in MeV/s/fission.
Uncertainties for operational parameters, manufacturing tolerances, and burnup-induced technological changes.
Parameter values for a and b as a function of the time after shutdown t for equation (B.12).
List of nuclei updated in JEFF-3.1.1 with the Greenwood’s TAGS mean decay energy for light particle component (ELP). The values from the different versions of JEFF and ENDF/B libraries are also included for comparison.
List of nuclei updated in JEFF 3.1.1 with the Greenwood’s TAGS mean decay energy for the electromagnetic component (EEM). The values from the different versions of JEFF and ENDF/B libraries are also included for comparison.
List of nuclei measured per the Total Absorption Gamma Spectroscopy method per the TAS and MTAS collaborations with the associated mean decay energy for light particle (ELP). The values from the different versions of JEFF, JENDL and ENDF/B libraries are also included for comparison. The TAGS values already included in the different versions of libraries are in grey.
List of nuclei measured per the Total Absorption Gamma Spectroscopy method per the TAS and MTAS collaborations with the associated mean electromagnetic decay energy (EEM). The values from the different versions of JEFF, JENDL and ENDF/B libraries are also included for comparison.The TAGS values already included in the different versions of libraries are in grey.
All Figures
 |
Fig. 1. Examples of calculated decay heat for typical UO2 assemblies (top), having different burnup and enrichment values; bottom: comparison between typical MOX and UO2 SNF assemblies. |
| In the text | |
 |
Fig. 2. Histogram of the ratios of calculated (C) over experimental (E) decay heat values from literature studies for calorimetric measurements of full fuel assemblies. Both PWR and BWR assemblies are included. |
| In the text | |
 |
Fig. 3. Number of nuclides that have to be computed to obtain a fraction (99%, 99.9%,..., 100% – ϵ, with ϵ = 10−12%) of the total decay heat computed by DARWIN with the JEFF-3.0 nuclear data library. Left: short cooling time in seconds from 0.1 to 1013 seconds. Right: long cooling time in days from 1 day to 1011 years. |
| In the text | |
 |
Fig. 4. Comparison between the CASMO5 (single-assembly calculation, left) and SIMULATE (full-core calculation right) pin burnup values for the GU3 sample. The sample location is indicated with an orange square [33]. |
| In the text | |
 |
Fig. 5. Burnup differences for assembly and pin values, for a realistic cycle calculation, from two different versions of the same core simulator. |
| In the text | |
 |
Fig. 6. Contributions to the UO2 SNF decay heat for 5 years of cooling time. Numbers 3, 4, and 5 correspond to the initial 235U enrichment. |
| In the text | |
 |
Fig. 7. Actinide production scheme in irradiated reactor fuel. |
| In the text | |
 |
Fig. 8. Build-up of the Pu isotopes in a LWR as a function of the assembly burnup. |
| In the text | |
 |
Fig. 9. Fission rate fraction as a function of burnup for the UO2 model in reference [43]. |
| In the text | |
 |
Fig. 10. Build up of the 106Rh nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
| In the text | |
 |
Fig. 11. Build up of the 144Ce nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
| In the text | |
 |
Fig. 12. Build up of the 134Cs nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
| In the text | |
 |
Fig. 13. Build up of the 137Cs nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
| In the text | |
 |
Fig. 14. Build up of the 90Sr nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
| In the text | |
 |
Fig. 15. Build up of the 154Eu nuclide in a LWR as a function of the assembly burnup, for the main four fissioning nuclides. |
| In the text | |
 |
Fig. 16. Sketch of the HEDL [70] (left) and GE-Morris calorimeter [71] (right). |
| In the text | |
 |
Fig. 17. Layout of the MERCI device at the OSIRIS facility [86]. |
| In the text | |
 |
Fig. 18. Sketch of the MOSAÏC calorimeter [89]. |
| In the text | |
 |
Fig. 19. Gamma-ray heat loss fraction [86]. |
| In the text | |
 |
Fig. 20. Calculation over measurement discrepancies (red line) associated with the total uncertainty (measurement, modeling, and nuclear data) at two standard deviations [94]. |
| In the text | |
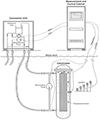 |
Fig. 21. Sketch of the Clab calorimeter [76]. |
| In the text | |
 |
Fig. 22. Layout of KKG calorimeter (left) and cross-section of the shielding design (right). |
| In the text | |
 |
Fig. 23. Left: Side view of the critical core and HPGe detector. Yellow lines are of aluminum alloy. Right: Measured γ-ray spectrum for critical core. |
| In the text | |
 |
Fig. 24. Left: Time of flight spectrum for estimation of energy of incident neutron. Right: γ-ray spectrum at time background. Nuclides in labels denote β-decay parents of delayed γ-rays. |
| In the text | |
 |
Fig. 25. Decay heat ratio P/P0 as presented in equations (8)–(B.12), compared to the early ANS-5.1/N18.6 standard from 1971. The irradiation time T is considered infinite (1013 seconds). |
| In the text | |
 |
Fig. 26. Example of decay heat (with delayed fission); Top: for a UO2 fuel, enriched at 3.5%, with a burnup value of 33 MWd/kgU. Bottom: Same for a MOX fuel enriched at 5.30% (Pu content) with a burnup value of 60 MWd/kgHM. Extracted from a French REP900 [133]. |
| In the text | |
 |
Fig. 27. Top: comparison of the data presented in Table 16 (dashed lines are the values from the code 1 to 5). Bottom: Comparison for the standard only, with both irradiation histories. |
| In the text | |
 |
Fig. 28. Total and electromagnetic decay heat component for pulse irradiation of 235U (top) and 239Pu (bottom) with thermal neutrons. |
| In the text | |
 |
Fig. 29. Example of weighted cumulative fission yields, before and at the end of irradiation, for two UO2 and MOX assemblies. |
| In the text | |
 |
Fig. 30. Schematic picture of the Pandemonium effect. |
| In the text | |
 |
Fig. 31. Left: light particles decay heat component for pulse irradiation of 235U with thermal neutrons. Right: same for the electromagnetic decay heat component. |
| In the text | |
 |
Fig. 32. Left: light particles decay heat component for pulse irradiation of 239Pu with thermal neutrons. Right: same for the electromagnetic decay heat component. |
| In the text | |
 |
Fig. 33. Impact of fission yield libraries on electromagnetic decay heat component for pulse irradiation of 239Pu with thermal neutrons. |
| In the text | |
 |
Fig. 34. Total decay heat generation rate in Kozloduy NPP unit 6, Spent Fuel Pool: (a) 2014-2015 uncertainty evaluation; (b) 2018–2019 uncertainty evaluation; (c) 2014–2015 bounding data; and (d) 2018–2019 bounding data. |
| In the text | |
 |
Fig. 35. Decay heat simulation methodology with SCALE [269]. Left: generation of ORIGEN reactor library. Right: ORIGEN depletion and decay simulation. |
| In the text | |
 |
Fig. 36. Radioactivity (left) and photon intensity (right) from debris of Fukushima-Daiichi nuclear power plant estimated from the decay data of JENDL-5, JENDL/DDF-2015, JEFF-3.3, and ENDF/B-VIII.0 (data are provided by courtesy of T. Matsumura (CLADS, JAEA)) |
| In the text | |
 |
Fig. A.1. Schematic view of the PHENIX reactor. |
| In the text | |
 |
Fig. A.2. Comparison of calculated and measured decay heat [332]. |
| In the text | |
 |
Fig. C.1. Relative contribution of 90Sr→90Y to total decay heat. |
| In the text | |
 |
Fig. C.2. Calculated energy deposition in HPGe detector. |
| In the text | |
 |
Fig. C.3. Relative contribution of Bremsstrahlung ray from beta decay of 90Y to the total count rate in the pulse height region from 1.6 to 1.87 MeV. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



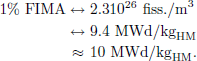
![$$ \begin{aligned} ^{238}\text{ U} \xrightarrow []{(n,\gamma )} {^{239}\text{ U}} \xrightarrow [(23.46~\text{ min})]{\beta } {^{239}\text{ Np}}\xrightarrow [(2.356~\text{ day})]{\beta } {^{239}\text{ Pu}}. \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq2.gif)
![$$ \begin{aligned} ^{237}\text{ Np} \xrightarrow []{(n,\gamma )} {^{238}\text{ Np}} \xrightarrow [(2.1~\text{ days})]{\beta } {^{238}\text{ Pu}}. \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq3.gif)
![$$ \begin{aligned} ^{243}\text{ Am} \xrightarrow []{(n,\gamma )} {^{244}\text{ Am}} \xrightarrow [(10.1~\text{ h}/26~\text{ min})]{\beta } {^{244}\text{ Cm}}. \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq4.gif)
![$$ \begin{aligned} ^{241}\text{ Pu} \xrightarrow []{(n,\gamma )} {^{242}\text{ Pu}} \xrightarrow []{(n,\gamma )} {^{243}\text{ Pu}}\xrightarrow [(4.96~\text{ h})]{\beta } {^{243}\text{ Am}}. \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq5.gif)
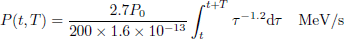
![$$ \begin{aligned} = 4.1\times 10^{11}P_0 \left[t^{-0.2} - (t+T)^{-0.2}\right]\quad \text{ MeV/s} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq106.gif)
![$$ \begin{aligned} = 0.065P_0 \left[t^{-0.2} - (t+T)^{-0.2}\right]\quad \text{ W,} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq107.gif)
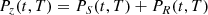
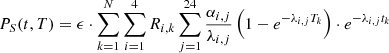
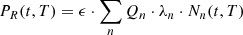


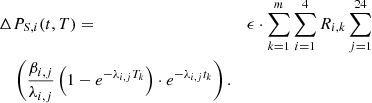
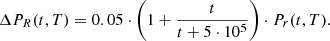
![$$ \begin{aligned} P_T(t,T)&= \left[P_F(t,T)+P_c(t,T)+P_E(t,T)\right. \nonumber \\&+ \left. P_A(t,T)+P_S(t,T)\right]\cdot F_s(t) \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq16.gif)
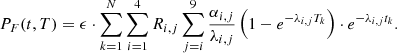
![$$ \begin{aligned} P_c(t,T)&= Y\cdot E\cdot \lambda _4\frac{S}{Q}\left[\frac{1-e^{-(\lambda _4+\sigma _4\phi )T}}{\lambda _4+ \sigma _4\phi }\right.\nonumber \\&+ \left. \frac{e^{-\sigma _3\phi T}-e^{-(\lambda _4+\sigma _4\phi ) T}}{\sigma _3\phi -(\lambda _4+\sigma _4\phi )}\right]e^{-\lambda _4 t} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq18.gif)
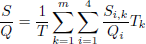
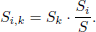
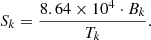
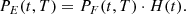
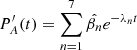
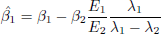
![$$ \begin{aligned} \hat{\beta _2}&= \beta _2\left[1+\frac{E_1}{E_2}\frac{\lambda _1}{\lambda _1-\lambda _2}\right] \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq109.gif)

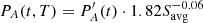
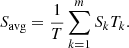
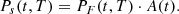
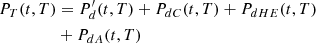
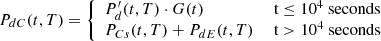
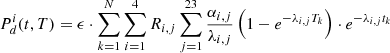
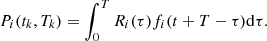
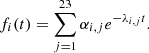
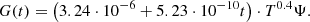
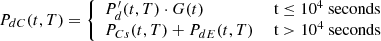
![$$ \begin{aligned} P_{dCs}(t,T)&= Y\cdot E\cdot \lambda _4\frac{P}{Q}\left[\frac{1-e^{-(\lambda _4+\sigma _4\phi )T}}{\lambda _4+\sigma _4\phi }\right.\nonumber \\&\cdot&\left. \frac{e^{-\sigma _3\phi T}-e^{-(\lambda _4+\sigma _4\phi )T}}{\sigma _3\phi -(\lambda _4+\sigma _4\phi )}\right]\cdot e^{-\lambda _4 t} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq36.gif)
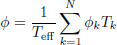
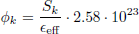
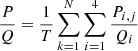
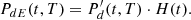
![$$ \begin{aligned} P_{dHE}(t,T)=\frac{P_{\rm max}}{Q_{\rm eff}}\left[F_U(t,T)+F_{Np}(t,T)\right] \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq40.gif)
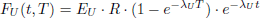
![$$ \begin{aligned} F_{Np}(t,T)&= E_{Np}\cdot R \left[\frac{\lambda _U}{\lambda _U-\lambda _{Np}}\left( 1-e^{-\lambda _{Np}T}\right)e^{-\lambda _{Np}t}\right.\nonumber \\&-&\left. \frac{\lambda _{Np}}{\lambda _U-\lambda _{Np}}\left(1-e^{-\lambda _U T}e^{-\lambda _U t}\right)\right] \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq112.gif)
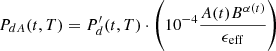
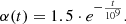
![$$ \begin{aligned} \left[\frac{\Delta P_d}{P_d}\right]^2= \left[\frac{\Delta P^{\prime }_d}{P^{\prime }_d}\right]^2 + \left[\frac{\Delta P}{P}\right]^2 \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq44.gif)
![$$ \begin{aligned} \left(\Delta P^i_d(t,T)\right)^2&= \sum _{i=1}^4\left[ \left(\frac{\Delta Q_i}{Q}\right)^2 + \right. \nonumber \\&\left. \frac{1}{Q_iP^{\prime }_{di}}\left( \sum _{k=1}^{N}P_{i,k}\sum _{j=1}^{23}\frac{\beta _{i,j}}{\lambda _{i,j}}\left(1-e^{-\lambda _{i,j}T_k}\right)\right)^2 \right. \nonumber \\&\left.\left( \cdot e^{-\lambda _{i,j}t_k} \right)^2 \right]. \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq45.gif)
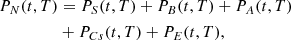
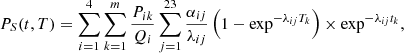
![$$ \begin{aligned} P_B(t,T)=\sum _{k=1}^m\frac{P_k}{Q}\left[F_U(t_k,T_k)+F_{Np}(t_k,T_k)\right]. \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq48.gif)
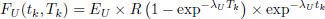
![$$ \begin{aligned} \displaystyle F_{Np}(t_k,T_k)&= E_{Np}\times R\Bigg [\frac{\lambda _U}{\lambda _U-\lambda _{Np}} \left(1-\exp ^{-\lambda _{Np}T_k}\right)\nonumber \\&\displaystyle \times&\left. \exp ^{-\lambda _{Np}t_k}\right. \nonumber \\&\displaystyle -&\displaystyle \left. \frac{\lambda _{Np}}{\lambda _U-\lambda _{Np}} \left(1-\exp ^{-\lambda _{U}T_k}\right)\right. \nonumber \\&\displaystyle \times&\exp ^{-\lambda _{U}t_k} \Bigg ] \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq113.gif)
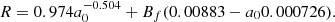
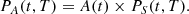
![$$ \begin{aligned} P_{Cs}(t,T)&= \frac{P}{Q}\lambda _4E_{Cs}y\left[ \frac{1-\exp ^{-(\lambda _4+\sigma _4\Phi _{eff})T_{eff}}}{\lambda _4+\sigma _4\Phi _{eff}} \right.\nonumber \\&+ \left. \frac{\exp ^{-(\sigma _3\Phi _{eff}T_{eff})}-\exp ^{-(\lambda _4+\sigma _4\Phi _{eff})T_{eff}}}{\sigma _3\Phi _{eff}-(\lambda _4+\sigma _4\Phi _{eff})} \right]\nonumber \\&\cdot&\exp ^{-\lambda _4t} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq52.gif)
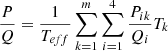
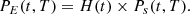
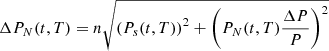
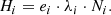
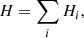
![$$ \begin{aligned} \frac{\mathrm{d}N_i(t)}{\mathrm{d}t} =&\sum _j \left[\left(b_{j\rightarrow i}\lambda _j + \sum _p\phi _p\langle \sigma _{p,j\rightarrow i}\rangle \right)\cdot N_j(t)\right.\nonumber \\&\left.-\left(\lambda _i + \sum _p \phi _p\langle \sigma _{p,i}\rangle \right)\cdot N_i(t)\right] \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq60.gif)
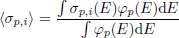

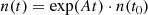
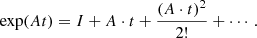
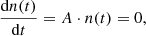
![$$ \begin{aligned} \pm \Delta m_{1,2}&= \pm \frac{\pi }{4}l \rho _{UO_2} \Bigg [ 2 \Delta d_{\rm fout} \Delta d_{\rm fout}+2d_{\rm fin} \Delta d_{\rm fin}\nonumber \\&+ \frac{\Delta \rho _{UO_{2}}}{\rho _{UO_{2}}} ( d_{\rm fout}^{2} + d_{\rm fin}^{2} ) \Bigg ] . \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq73.gif)
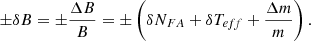
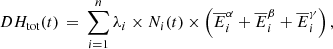
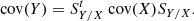
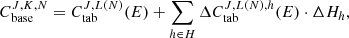
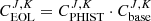

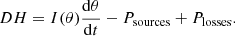
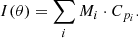
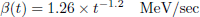
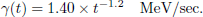
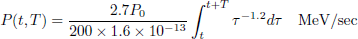
![$$ \begin{aligned} = 4.1\times 10^{11}P_0 \left[t^{-0.2} - (t+T)^{-0.2}\right]\quad \text{ MeV/sec} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq116.gif)
![$$ \begin{aligned} = 0.065P_0 \left[t^{-0.2} - (t+T)^{-0.2}\right]\quad \text{ Watts}. \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq117.gif)
![$$ \begin{aligned} P(t,T)&= 0.1P_0\left[(t+10)^{-0.2}-0.87(t+2\times 10^{7})^{-0.2}\right.\nonumber \\&-&\left. (t+T+10)^{-0.2} \right. \nonumber \\&-&\left. 0.87(t+T+2\times 10^{7})^{-0.2}\right]\quad \text{ Watts} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq95.gif)
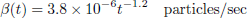
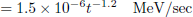
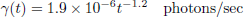
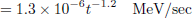
![$$ \begin{aligned} P(t,T)&= P_0\times 0.095 t^{-0.26}\left[ 1-\left( 1+\frac{T}{t}\right)^{-0.2}\right]. \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq98.gif)
![$$ \begin{aligned} P(t,T)&= 0.005P_0\times a \left[t^{-b} - (t+T)^{-b}\right]\quad \text{ Watts} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn240001/epjn240001-eq99.gif)