| Issue |
EPJ Nuclear Sci. Technol.
Volume 3, 2017
|
|
|---|---|---|
| Article Number | 21 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/epjn/2017015 | |
| Published online | 30 June 2017 | |
https://doi.org/10.1051/epjn/2017015
Regular Article
Reassessment of gadolinium odd isotopes neutron cross sections: scientific motivations and sensitivity-uncertainty analysis on LWR fuel assembly criticality calculations
1
ENEA, Italian National Agency for New Technologies, Energy and Sustainable Economic Development, Centro Ricerche “E. Clementel”,
Via Martiri di Monte Sole, 4,
40129
Bologna, Italy
2
Department of Physics and Astronomy, University of Bologna,
Via Irnerio, 46,
40126
Bologna, Italy
3
INFN,
Via Irnerio, 46,
40126
Bologna, Italy
* e-mail: federico.rocchi@enea.it
Received:
8
November
2016
Received in final form:
11
May
2017
Accepted:
2
June
2017
Published online: 30 June 2017
Gadolinium odd isotopes cross sections are crucial in assessing the neutronic performance and safety features of a light water reactor (LWR) core. Accurate evaluations of the neutron capture behavior of gadolinium burnable poisons are necessary for a precise estimation of the economic gain due to the extension of fuel life, the residual reactivity penalty at the end of life, and the reactivity peak for partially spent fuel for the criticality safety analysis of Spent Fuel Pools. Nevertheless, present gadolinium odd isotopes neutron cross sections are somehow dated and poorly investigated in the high sensitivity thermal energy region and are available with an uncertainty which is too high in comparison to the present day typical industrial standards and needs. This article shows how the most recent gadolinium cross sections evaluations appear inadequate to provide accurate criticality calculations for a system with gadolinium fuel pins. In this article, a sensitivity and uncertainty analysis (S/U) has been performed to investigate the effect of gadolinium odd isotopes nuclear cross sections data on the multiplication factor of some LWR fuel assemblies. The results have shown the importance of gadolinium odd isotopes in the criticality evaluation, and they confirmed the need of a re-evaluation of the neutron capture cross sections by means of new experimental measurements to be carried out at the n_TOF facility at CERN.
© F. Rocchi et al., published by EDP Sciences, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Fuel assemblies (FAs) of light water reactors (LWRs) (such as PWRs, BWRs, or VVERs) of 2nd and 3rd generations make extensive recourse to s.c. “burnable neutron poisons” in various forms and technical solutions. These burnable poisons are chosen among those isotopes having thermal neutron capture cross sections comparable or higher than the thermal neutron fission cross section of 235U; they are in fact used as competitors to 235U in the absorption of thermal neutrons, in such a way that, being their absorption parasitic for the neutron chain reaction, they can compensate an initial higher fuel enrichment that, for safety reasons, could not be inserted in the fuel pins. As soon as the fuel in the FAs is burnt during the operation of a given reactor, both 235U and burnable poisons are depleted so that the compensating effect of the poisons is neutralized at a point in the cycle of the fuel at which the remaining amount of fissile material can be controlled easily and safely by other available means. This idea can naturally increase the overall length of the fuel cycle by allowing higher amounts of fissile material, which correspond to higher enrichments in 235U, loaded in FAs and then in reactor cores. This, of course, means in turn better economy of both the nuclear fuel and of the management of reactors: fuel reloading into cores can be done after longer periods of uninterrupted operation [1].
Several types and forms of burnable poisons have been successfully tested over the past decades; the most common one being gadolinia (Gd2O3) mixed directly within the UO2 fuel matrix; this insures that the burnable poison is never separated from the active material it must control and also enhances mechanical properties of the fuel. Gadolinium oxide is, therefore, a kind of dopant within the UO2 material itself. The absorption of thermal neutrons is of course provided by the odd isotopes 157Gd and, to a far lesser extent, 155Gd. Gadolinium is used, for the sake of simplicity, in its natural isotopic composition. Its first use in a commercial reactor dates back to 1973.
To give an example, gadolinia as burnable poison is used presently, and since 2002, in the s.c. Cyclades and Gemmes core managements schemes by Electricité de France in its CP0 and 1300 MWe PWR reactors, respectively [2,3]. Not all FAs in a core contain fuel pins doped with gadolinium; the Gemmes scheme, for instance, foresees a reload of 64 FAs (corresponding to 1/3 of the whole core), 24 of which contain some pins with Gd2O3 mixed to UO2 [2]. The choice of the position within a core where FAs with gadolinium fuel pins are placed is also dictated by an optimization of the power density distribution; such an optimization also favors the achievement of higher thermal safety margins for these reactors.
Gadolinium isotopes cross sections are therefore crucial in assessing the neutronic performances and safety features of FAs and whole cores. The proper knowledge of these cross sections is not only relevant at the beginning of life of a FA, but also during its life cycle; in fact, accurate predictions of the burning rate of odd isotopes are fundamental in the prediction of the appearance of the FA reactivity peak and its intensity. In turn, these two parameters are of utmost importance in the assessment of the criticality safety margins for the storage of partially burnt fuel inside Spent Fuel Pools (SFPs) of reactors, especially during postulated loss-of-coolant or loss-of-cooling accidents at these storage facilities [4]. The correct prediction of the 3D spatial distribution of the gadolinium isotopes remaining within a partially burnt FA that has been put in interim storage in an SFP, possibly during a refueling outage of the reactor, is fundamental for a correct estimate of the criticality safety margins of SFPs. It must be remembered in fact that the neutron flux distribution inside a core is far from uniform, with both axial and radial gradients, which produce a non-uniform burning of both fissile isotopes and gadolinium isotopes.
A good prediction of the depletion of gadolinium isotopes is also necessary to estimate the s.c. “residual reactivity penalty” that is essentially the value of anti-reactivity associated to the high-burnup, equilibrium concentrations of odd and even isotopes; this value is important because if it is too high, it can induce a limitation on the total amount of time a given FA can be used at full power. This effect is unavoidable but should be well predictable to foresee a good fuel management scheme. To give just a rough example, the reactivity penalty due to 16 gadolinium fuel pins with initial 8.0 wt.% of gadolinia in UO2 for a 17×17 PWR FA (average 235U enrichment of 4.5 wt.%) corresponds roughly to the “loss” of 5 full-power days per year [5]. In the electricity energy market of France, 5 full-power days of an III-Generation EPR reactor tally roughly to 8 M€ [6].
A more accurate assessment of gadolinium isotopes cross sections is also essential for CANDU reactors. In fact, in the case of severe accidents due to or leading to criticality excursions, gadolinium nitrate is injected into the heavy water moderator, to reduce/eliminate criticality risk or excursions. Finally, it should be remembered that gadolinium isotopes are also fission products and are produced by the nuclear fuel as its burnup increases; they, therefore, act as neutron poisons also in their role of fission products and they must be accounted for in burnup and depletion calculations of FAs.
2 Scientific motivation
The necessity of an updating in the gadolinium odd isotopes cross sections evaluations is based on a series of quantitative scientific considerations. First of all, as it is shown in Figure 1, the current gadolinium odd isotopes (n,γ) cross sections (in the ENDF/B-VII.1 library) present, in the high sensitivity thermal energy range and to the best of the present knowledge, based on the existing experiments, non-negligible (5–10%) uncertainty values. Furthermore, the capture cross section of the odd gadolinium isotopes has not been extensively studied and is not known with the accuracy typically required by the nuclear industry. Looking at the EXFOR database, there seems to be available only one experimental point for 157Gd(n,γ) in the energy region below the resolved resonances, namely at 2200 m/s, which was determined to be roughly 264 000 b. This single data-point was published in 1958 and no uncertainty was associated to it [7]. Again in 1958, the BNL-325 Report instead gave a value of 240 000 b [8]. In 1960, a second set of data was extracted from total cross section measurements [9], which gave a value of 254 000 b. One has then to wait 2006 before having another measurement at 2200 m/s [10]: 226 000 b, about 11% lower with respect to the value assumed for the ENDF/B-VI.8 evaluation (254 000 b). Table 1 shows a summary of the scientific literature historical progression in the 157Gd neutron capture thermal cross sections evaluation as described above. Table 1 shows that even if considering only the recent (2003–2014) odd isotopes gadolinium capture cross sections evaluations, there is a significative (6–11%) deviation with respect to ENDF/B-VII reference (2006) data. For this reason, the uncertainty (0.3%) associated with the reference data cannot be considered a safe estimate for evaluating the actual range of values that could take the thermal cross section. Another scientific circumstance that suggests a necessity for an improvement of the gadolinium odd isotopes cross sections is the results of the French Commissariat à l'énergie atomique et aux énergies alternatives (CEA) qualification program for French LWR using the Melusine research reactor in Grenoble, prior to its shutdown and decommissioning. In the Gedeon-I experimental campaign (1982–1985), some discrepancies between experiments and calculations (based on JEFF-3.1.1) for the depletion of odd Gd isotopes had already been found, even though not very large [17]. The last experimental campaign, called Gedeon-II (1985–1988), consisted in the irradiation of a dedicated special 13×13 PWR FA containing gadolinia pins, up to about 13 GWd/MTU, followed by a very accurate post-irradiation examination in order to make it possible to compare experimental results to calculation predictions [18,19]. A total of 123 radiochemical data from the post-irradiation examinations are specifically dedicated to gadolinium isotopic content. The most recent experiment-to-calculation comparison is that of 2014 by Bernard and Santamarina [19] who used the Apollo2.8 reference deterministic code with multigroup cross section libraries based on the JEFF-3.1.1 evaluated library to simulate the Gedeon-II experiment. While the overall predictions on gadolinium isotopics look quite good, still some non-negligible biases are found for 157Gd. In detail, the relative error between calculated and experimental data is found to be roughly between 2% and 25%, depending on the specific level of burnup and intra-assembly position. While in certain cases this relative error is affected by a rather high uncertainty σ, such that sometimes 2σ cover this relative error, in many other cases this is not so. Moreover, this non-negligible bias – the ratio between calculated and experimental gadolinium odd isotopes concentrations has always a negative sign in each FA position and at every burnup level – probably points to the fact that the JEFF-3.1.1/157Gd(n,γ) evaluation in the experiment energy range is incorrect.
The impact of a recent measurement of the neutron capture and total cross sections and resonance parameters of gadolinium-isotope in the range 1–300 eV [10] has also been tested on BWR reactor physical parameters. In particular, a comparison between computational and experimental values of rod-by-rod total fission rate (C/E) and modified conversion ratio prediction was performed. The measured values have been produced in the framework of the LWR-PROTEUS – a joint research program between the Paul Scherrer Institut (PSI) and an association of the Swiss nuclear operators (Swissnuclear) – experiments in Switzerland. The calculation values were obtained using CASMO-4 with the real Gd vector and the JEF-2.2 and ENDF/B-VI libraries, and with the Gd effective vector – developed to take into account the newly measured cross sections – with the ENDF/B-VI library. This preliminary study showed that the effect of the newly measured gadolinium cross sections seems to have the potential to resolve, in part, some of the different trends observed between calculated and experimental values for the gadolinium-containing rods [20].
In the same context of the LWR-PROTEUS program (Phase I and III), a radial distribution of the total fission rate (Ftot) and the 238U-capture-to-total-fission (C8/Ftot) ratio was measured in BWR assemblies of the type of SVEA-96+ and SVEA-96 Optima2. The comparison of measured values with an MCNPX calculation has shown an underprediction of Ftot and an overprediction of C8/Ftot in the UO2–Gd2O3 pins when using cross sections obtained from ENDF/B-VI, JEFF-3.0, or JEFF-3.1. Predictions using the new set of gadolinium cross sections have been found to increase the calculated fission rates in the UO2–Gd2O3 pins and a much better agreement with the experimental values of the normalized Ftot radial distributions. No change was observed on the 238U captures because the flux change in the UO2–Gd2O3 pins above 0.625 eV is <0.1% [21].
Despite the circumstances previously described [20,21], the goodness of the newly evaluated data is not confirmed by tests performed on a set of the International Criticality Safety Benchmark Evaluation Project (ICSBEP) [22]. Table 2 shows a comparison between the reference and the evaluated criticality coefficient (Keff) as results from calculations with ENDF/B-VII, JEFF-3.1 and Leinweber et al. [10] cross sections data.
As results from Table 2, the use of the new gadolinium cross sections evaluated data does not involve any improvement (except for the LCT-035 C3 system) in the criticality coefficient evaluation.
Possible mistakes in the evaluation of the gadolinium cross sections data are also confirmed by some simulations that have recently been made in ZED-2 (Zero Energy Deuterium) critical facility at the Chalk River Laboratories, AECL, to study the reactivity effect up to 1.5 ppm of gadolinium in the moderator. The experiments at ZED-2 and their comparison with simulations were conducted just because the most recent evaluation [10] could have posed serious safety concerns to CANDU reactors in case it was confirmed. One of the results of the study is the investigation of the quantitative effect on the k-effective value using various sources of gadolinium neutron capture cross sections in an MCNP simulation of the reactor system. In detail, the gadolinium cross sections adopted have been the ENDF/B-VII.1 [23]. The multiplication coefficient evaluation of the ZED-2 facility obtained by means of an MCNP simulation has shown, with respect to the experimental values, an eigenvalue overestimation using the ENDF/B-VII.1 [10] data and an underestimation using the ENDF/B-VII.0 data. The obtained results show, once again, the need for a re-evaluation of the gadolinium odd isotopes capture cross sections data that appear overestimated in the ENDF/B-VII.0 and underestimated in the beta version of the ENDF/B-VII.1 [10]. Further on, pile-oscillation measurements performed in the MINERVE research reactor in Cadarache [24] also show strong inconsistencies with the microscopic measurements at RPI [10] for the 2200 m/s capture cross section for natGd; the MINERVE result was 49 360 ± 790 b, which was in rather good agreement with the JEFF-3.1.1 value of 48 630 b, while the RPI one was 44 200 ± 500 b.
Finally, concerning the overall behavior of the ENDF/B-VII.1, JENDL-4.0, and JEFF-3.1.1 evaluations for gadolinium isotopes, it is important to quote the gigantic work performed by van der Marck [25] published in 2012. In this work, more than 2000 benchmarks from the ICSBEP database were calculated with MCNP6 using the above-mentioned evaluated libraries. The use of a Monte Carlo code to analyze the benchmarks ensures that no calculation error due to self-shielding of strong absorbers has been introduced. The total number of calculated benchmarks which contain gadolinium amounts to 164. All of them come from zero-power experiments without burnup and depletion of gadolinium isotopes, therefore capable of providing indications on the behavior of the evaluations independently from the consumption of Gd odd isotopes and buildup of Gd even isotopes. All these calculated benchmarks are characterized by thermal spectra, both with solid fuel and with solution systems. The results show strong discrepancies between experimental and calculated values; the C/E − 1 values range between −2000 and +1500 pcm, well beyond the experimental uncertainties; the three evaluated libraries provide rather similar results. In particular, the very important class of LCT systems, composed of 74 benchmarks, yields values of C/E − 1, averaged over all the 74 cases of the class, between −578 pcm (JEFF-3.1.1) and −499 pcm (JENDL-4.0). The general conclusion by van der Marck, comparing the results from all the 2000 calculated benchmarks, is that at least some part of the C/E − 1 is to be attributed to gadolinium isotopes.
All in all, there seems to be space and justification for newer and improved experimental cross section determinations in the low energy range, especially targeted to 157Gd(n,γ), to which very accurate uncertainty and covariance values should also be added in order to improve the neutronic analyses of nuclear fuels.
 |
Fig. 1 Relative standard deviation of 155Gd and 157Gd capture cross sections. |
List of evaluations of 157Gd thermal capture cross sections as reported in scientific literature.
Keff comparison values of a series of ICSBEP experiments.
3 Sensitivity and uncertainty theory
In this paragraph, a short presentation of the theoretical background of sensitivity and uncertainty analysis is reported. A more detailed discussion of the sensitivity and uncertainty theory is reported in [26].
3.1 Sensitivity
An integral reactor parameter Q (i.e., fundamental eigenvalue, reaction rate, reactivity coefficient) is a complex mathematical function of its independent cross sections data parameters:
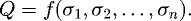 (1)
(1)
Uncertainty in the evaluation of the independent parameters involves a deviation of the integral parameter with respect to its nominal value. A possible mathematical evaluation of such deviation can be performed by developing relationship (1) in a Taylor series around a nominal value:
 (2)
(2)
If the variations of all independent cross sections variables with respect to the nominal value are such that in (2) the second order term can be neglected (i.e., if it appears that (Δσi)2 ≪ 1 ∀ i), it's reasonable to truncate the Taylor series at first order:
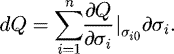 (3)
(3)
Relationship (3) can be expressed in a more general form by introducing the relative difference of the integral and physical parameters:
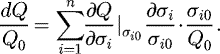 (4)
(4)
Relative variation of Q due to the change of an independent cross section data parameters can be expressed in terms of a sensitivity coefficient as follows:
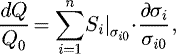 (5)
where the sensitivity coefficients are formally given by:
(5)
where the sensitivity coefficients are formally given by:
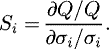 (6)
(6)
Relationship (6) assesses how a given cross section is important in the estimation process of Q, as a function of the incident neutron energy; it is capable of estimating how much, and in which energy region, an error in the cross section propagates to an error in Q. A complete sensitivity coefficient is characterized by two components as follows:
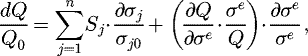 (7)
where the first and second terms on the right side of (7) are generally denoted as indirect (I) and direct (D) effects, respectively. The D term is the contribution to the variation of the integral parameter Q, as a direct function of a generic cross section σe, due to a simple variation of the energy dependent cross section of interest σe only. However, Q may also be a direct function of the neutron flux Φ, which in turn is a function of all the n cross sections σj of a given system, so that a variation in σe may propagate first into a variation of Φ and, through this, into a variation of Q. This effect is represented by the I term, an indirect contribution to dQ due to a flux perturbation originally caused by a variation of σe. The indirect term consists, more precisely, of two components, namely, the explicit and implicit ones. The explicit component comes from a flux perturbation caused by perturbing any multi-group cross-section appearing explicitly in the transport equation. The implicit component is associated with a flux perturbation due to a change of the self-shielding of a nuclide by means of a perturbation of the cross sections of another nuclide, so that a variation of σe first causes a variation of all the other cross sections σj, and then of the flux. For example, if one considers hydrogen, perturbing the H elastic value has an explicit effect because the flux is perturbed due to change in H moderation. However, there is also an implicit effect because changing the H data causes another flux perturbation because of a perturbation in the absorption cross section of 238U due to a change in self-shielding [27].
(7)
where the first and second terms on the right side of (7) are generally denoted as indirect (I) and direct (D) effects, respectively. The D term is the contribution to the variation of the integral parameter Q, as a direct function of a generic cross section σe, due to a simple variation of the energy dependent cross section of interest σe only. However, Q may also be a direct function of the neutron flux Φ, which in turn is a function of all the n cross sections σj of a given system, so that a variation in σe may propagate first into a variation of Φ and, through this, into a variation of Q. This effect is represented by the I term, an indirect contribution to dQ due to a flux perturbation originally caused by a variation of σe. The indirect term consists, more precisely, of two components, namely, the explicit and implicit ones. The explicit component comes from a flux perturbation caused by perturbing any multi-group cross-section appearing explicitly in the transport equation. The implicit component is associated with a flux perturbation due to a change of the self-shielding of a nuclide by means of a perturbation of the cross sections of another nuclide, so that a variation of σe first causes a variation of all the other cross sections σj, and then of the flux. For example, if one considers hydrogen, perturbing the H elastic value has an explicit effect because the flux is perturbed due to change in H moderation. However, there is also an implicit effect because changing the H data causes another flux perturbation because of a perturbation in the absorption cross section of 238U due to a change in self-shielding [27].
3.2 Uncertainty
The uncertainties are associated to the cross sections and can be expressed, for a generic number of nuclides, in a mathematical formulation defining a variance-covariance matrix that, with respect to a nuclear reaction r, takes the following form:
 (8)
where the generic element cij of (8) represents the variance
(8)
where the generic element cij of (8) represents the variance 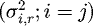 and covariance (σi,rσj,r ; i ≠ j) of the nuclear data. The cross sections uncertainty (cij), convoluted with the sensitivity (Sj), gives the related uncertainty to be associated in the evaluation of Q. The uncertainty of the Q integral parameter can be expressed as:
and covariance (σi,rσj,r ; i ≠ j) of the nuclear data. The cross sections uncertainty (cij), convoluted with the sensitivity (Sj), gives the related uncertainty to be associated in the evaluation of Q. The uncertainty of the Q integral parameter can be expressed as:
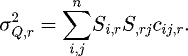 (9)
(9)
Relationship (9) can also be expressed in terms of a vector-matrix formulation as follows:
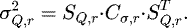 (10)
(10)
The introduction of a sensitivity matrix defined as a dyadic product of the sensitivity vector (Si) and its transposed 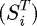 :
:
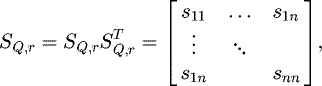 (11)
allows to represent the relative variance of the integral parameter Q in a more compact form as a dyadic product between two matrices [28]:
(11)
allows to represent the relative variance of the integral parameter Q in a more compact form as a dyadic product between two matrices [28]:
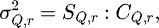 (12)where SQ,r is the sensitivity matrix and CQ,r is the variance-covariance matrix.
(12)where SQ,r is the sensitivity matrix and CQ,r is the variance-covariance matrix.
4 Calculation tools
The sensitivity and uncertainty (S/U) codes in SCALE 6.1 are collectively referred to as TSUNAMI (Tools for Sensitivity and Uncertainty Analysis Methodology Implementation) [29]. The S/U analysis results presented in this paper have been performed using TSUNAMI-2D, a functional module of the SCALE 6.1 control module TRITON (Transport Rigor Implemented with Time-Dependent Operation for Neutronic depletion), and carried out to determine response sensitivity and uncertainty. The S/U calculations are completely automated to perform: (a) cross sections self-shielding operations, (b) forward and adjoint transport calculations, (c) computation of sensitivity coefficients, and (d) calculation of the response uncertainty [30]. The calculation procedure for the (a) step is based on a rigorous mechanism using the continuous energy solvers BONAMIST and CENTRM for self-shielding in the unresolved and resolved resonance regions, respectively, for appropriately weighting multi-group cross-sections using a continuous energy spectrum. The CENTRM module performs transport calculations using ENDF-based point data on an ultrafine energy grid (typically 30 000–70 000 energy points) to generate effectively continuous energy flux solutions in the resonance and thermal ranges. This is used to weight the multi-group cross sections to be utilized in the subsequent transport calculations. After the cross-sections are processed, the TSUNAMI-2D sequence performs two criticality calculations, solving the forward and adjoint forms of the Boltzmann equation, respectively, using the NEWT bidimensional discrete ordinate code. In this step, an energy discretization based on a 238-groups structure is adopted. The sequence then calls the SAMS module in order to compute the sensitivity coefficients. Once the sensitivities are available, the uncertainty on the integral parameters of interest due to the uncertainty in the basic nuclear data is evaluated according to (12) using the so-called 44 GROUPCOV covariance matrix. The 44GROUPCOV matrix comprehends a total of 401 isotopes in a 44-group energy structure. The library includes “low fidelity” (lo-fi) covariances spanning the full energy range that consists of ORNL covariances based on the integral approximation in the thermal and epithermal ranges, combined with approximate uncertainties generated by the Brookhaven National Laboratory (BNL) and Los Alamos National Laboratory (LANL) in the high energy range above 5.5 keV. The high energy covariance data were generated with nuclear model codes and included uncertainties for inelastic (n,2n), capture, fission, and elastic reactions. In addition to lo-fi covariances, LANL has provided full range “high fidelity” evaluations for elements lighter than fluorine. This is a significant benefit for addressing moderator materials. Table 3 summarizes the sources of covariance data in the SCALE-6 covariance library [31].
TSUNAMI-2D simulations have been executed using the v7-238 SCALE cross sections libraries based on the ENDF/B-VII (release 0) library. The adjoint and forward transport calculations have been performed with the following convergence numerical criteria: 10−5 for the critical eigenvalue and 10−4 for the inner and outer spatial convergence iterations. The quadrature and scattering orders (Sn and Pn) respectively have been set to 16 and 1 (2 only for the moderator material). The iterative transport solutions have been accelerated using a coarse-mesh finite-difference approach (CMFD).
Sources of covariance data in the SCALE 6.1.3 covariance library.
5 Calculation models
In order to quantify the maximum impact of the uncertainty of the gadolinium isotopes cross sections on the criticality of a LWR system, calculations have been performed on two types of PWR FAs – that present the highest number of gadolinium fuel pins among the 17×17 EPR™ FA configurations [32,33] – and on three types of BWR FA systems with fuel pins containing gadolinium. In particular, the FAs studied are: the UK-EPR FA (UK-EPR-A, UK-EPR-B), the US-EPR FA (US-EPR-C3), the 7×7 BWR FA (GE7×7) used at the Peach Bottom USA reactor, the General Electric 9×9-7 BWR FA (GE9×9-7), the General Electric 10×10-8 BWR FA (GE10×10-8). The details of physical parameters used for the FAs analyzed are reported in Table 4. Figures 2 and 3 show a material and geometrical representation of the PWR and BWR assemblies configurations as described above.
Sensitivity and uncertainty analyses have been performed for the various cases listed in the previous table to compute the contribution of the gadolinium odd isotopes to the overall uncertainty in criticality eigenvalue evaluations and to investigate the effect of moderator density and the number of the gadolinium fuel pins to the global gadolinium odd isotope sensitivity in the FAs systems.
Technical specifications of PWR and BWR fuel assemblies.
 |
Fig. 2 U.K. EPR FA, enr. 5.0% @ 24 Gd fuel pins (left); U.S. EPR FA, enr. 3.25% @ 16 Gd fuel pins (center); U.K. EPR FA, enr. 3.2% @ 20 Gd fuel pins (right). |
 |
Fig. 3 GE BWR 10×10-8 @ 14 Gd fuel pins (left); GE BWR FA 9×9-7 @ 12 Gd fuel pins (center); GE BWR 7×7 @ 6 Gd fuel pins (right). |
6 Results and discussion
A series of NEWT/TSUNAMI-2D and SAMS5 calculations have been executed for each FA configuration listed in Table 4 to quantify the gadolinium odd isotopes sensitivities and uncertainties for the neutron multiplication factor k. In detail, the SU analysis has provided the uncertainty contributions, in decreasing importance order, to k of any nuclear reaction involved. In Table 5, the first 26 most significant contributors to the uncertainty of k for the GE10×10-8 FA at moderator density of 0.45 g/cm3 is given. The choice of the GE10×10-8 FA is due to the fact that this is the BWR configuration that contains the highest number of gadolinium fuel pins. It can be seen from the reported data that the (n,γ) reaction of odd isotopes 157Gd and 155Gd rank between 0.26 and 0.20 with respect to the most significant contributor which, therefore, has always rank set to one. Rank is here defined as the ratio between the contribution to uncertainty in keff of a particular couple of nuclide-reaction and the value of the maximum contribution to the uncertainty in keff.
It can be seen that 157Gd and 155Gd play the most important role immediately after that of 235U and 238U, whose data are either not measurable at present at the n_TOF facility or already under experimental investigation.
The results of the SU analysis of k with respect to 157Gd(n,γ) cross sections are presented in Figure 4. From this figure, it can be seen that the energy range of highest sensitivity to the 157Gd(n,γ) reaction is between about 0.1 eV and 1 eV. In the same figure, two profiles are actually given, at two different moderator densities; it can be seen that the overall shape of the sensitivity is little affected by this parameter. It can be concluded that any amelioration of 157Gd(n,γ) cross section in the 1/v energy range, particularly in the 0.1–1 eV range and especially if associated to low uncertainty values, can represent a real improvement in the overall assessment of the neutronic properties of the FAs here analyzed.
Figure 4 also shows that the impact of 157Gd(n,γ) is slightly higher for BWR FAs at lower moderator densities.
In Figure 5, the critical fluxes per unit lethargy as a function of neutron energy for the BWR GE10×10-8 FA, and for three different moderator densities, are given.
Finally, a sensitivity analysis of the effect of a different number (2, 4, 6) of gadolinium fuel pins on the k-effective in the BWR Peach Bottom 7×7 configuration has been performed. Figure 6 shows the obtained results.
From this figure, it can be concluded that the value of the sensitivity on the overall energy range is significantly influenced by the number of gadolinium fuel pins (roughly an average factor two every two fuel pins).
In Figure 7, the critical fluxes per unit lethargy as a function of the neutron energy for the BWR Peach Bottom 7×7 FA for 2, 4 and 6 gadolinium fuel pins are given.
An analysis of a different boron concentration has furthermore been performed on the US-EPR-C3 configuration. The results are presented in Table 6.
The total energy integrated sensitivity of the gadolinium odd isotopes is slightly higher in the no-boron configuration. This condition is in agreement with the physical circumstance that the configuration with boron presents a harder neutronic spectrum on which the high sensitivity thermal region of the gadolinium odd isotopes has less influence. The rank of the odd isotopes is virtually unaffected by the boron concentration.
In order to make a comparison between the different FAs analyzed, the total energy integrated sensitivities of 155Gd and 157Gd have also been evaluated; the results are reported in Table 7.
From the data of Table 7, it can be seen that, excluding the configuration which has only four gadolinium fuel pins, the impact of 155Gd(n,γ) and 157Gd(n,γ) is highest for BWR FAs at low moderator densities. The rank for 157Gd(n,γ) ranges from 0.12 to 0.28, while that for 155Gd(n,γ) ranges from 0.08 to 0.22. The impact on the k values due to gadolinium odd isotopes (n,γ) reactions could be from some tens to two or three hundreds pcm at most. However, any gain in the precision over the estimates of k is more than welcome to the nuclear industry and the nuclear safety authorities. Any improvement in cross section knowledge is therefore desired.
Contributions to overall uncertainty in criticality eigenvalue for the GE10×10-8 FA.
 |
Fig. 4 Profiles of sensitivity per unit of lethargy about 157Gd(n,γ) cross section as a function of incident neutron energy for the GE10×10-8 FA; the two curves refer to different moderator densities. |
 |
Fig. 5 Critical fluxes per unit lethargy for the BWR GE10×10-8 FA for three different moderator densities. |
 |
Fig. 6 Effect of number of gadolinium fuel pins on the sensitivity profile. |
 |
Fig. 7 Critical fluxes per unit lethargy for the BWR Peach Bottom 7×7 FA for 2, 4 and 6 gadolinium fuel pins. |
Effect of boron concentration on sensitivity and uncertainty data.
Energy integrated sensitivity and uncertainty values for the FAs analyzed.
7 Conclusions
A series of scientific results reported in the open literature shows that the use of gadolinium odd isotopes (157Gd and 155Gd) cross sections, currently implemented in the JEFF and ENDF/B-VII cross sections libraries, determines non-negligible differences in the evaluation of a system criticality with respect to experimental values. Even the most recent gadolinium odd isotopes cross sections evaluations do not produce an improvement in the criticality value predictions. An S/U analysis on commercial PWR and BWR assembly configurations has shown that gadolinium capture cross sections are among the most significant nuclide-reaction contributors to the uncertainty in the k-effective evaluation. For these reasons and starting from all the scientific arguments presented in this paper, a series of measurements to re-evaluate, with high accuracy and high resolution, the 157Gd and 155Gd neutron capture cross sections between thermal and 20 MeV neutron energy is currently in place at the n_TOF facility of the European Council for Nuclear Research (CERN) [34] and scheduled for completion before the end of the Summer 2016.
References
- K.W. Hesketh, in Encyclopedia of Material Science and Technology, edited by K.H.J. Buschow, R.W. Cahn, M.C. Flemings, B. Ilschner, E.J. Kramer, S. Mahajan, P. Veyssière (Elsevier, Amsterdam, 2002) [Google Scholar]
- H. Grard, Physique, fonctionnement et sûreté des REP (EDP Sciences, Les Ulis, 2014) [Google Scholar]
- N. Kerkar, P. Paulin, Exploitation des coeurs REP (EDP Sciences, Les Ulis, 2008) [Google Scholar]
- M. Adorni et al., Nuclear Energy Agency Report NEA/CSNI/R(2015)2, 2015 [Google Scholar]
- J.P.A. Renier, M.L. Grossbeck, Oak Ridge National Laboratory Report ORNL/TM-2001/38, 2001 [Google Scholar]
- French Law 1488, Nouvelle Organisation du Marché de l'Electricité, 2010 [Google Scholar]
- N.J. Pattenden, in Proceedings of the Second International Conference on the Peaceful Uses of Atomic Energy, Neutron Cross Sections, Session A-11, P/11, 16, 44 (1958) [Google Scholar]
- D.J. Hughes, R.B. Schwartz, US Government Printing Office, Neutron Cross Sections, BNL-325, Geneva, 1958 [Google Scholar]
- H.B. Møller, F.J. Shore, V.L. Sailor, Nucl. Sci. Eng. 8, 03 (1960) [Google Scholar]
- G. Leinweber et al., Nucl. Sci. Eng. 154, 03 (2006) [Google Scholar]
- R.B. Tattersell, H. Rose et al., J. Nucl. Energy Part A 12, 1 (1960) [Google Scholar]
- L.V. Groshev et al., Izv. Akad. Nauk SSSR Ser. Fiz. 26, 1119 (1962) [Google Scholar]
- L.V. Groshev et al. Bull. Acad. Sci. USSR Phys. Ser. 26, 1127 (1963) [Google Scholar]
- G.M. Sun, S.H. Byun, H.D. Choi, J. Radioanal. Nucl. Chem. 256, 03 (2003) [CrossRef] [Google Scholar]
- S.F. Mughabghab, Atlas of Neutrons Resonance Parameters and Thermal Cross Sections Z = 1–100, National Data Center Brookhaen National Laboratory Upton (Elsevier, Amsterdam, 2006) [Google Scholar]
- H.D. Choi et al., Nucl. Sci. Eng. 177, 2 (2014) [Google Scholar]
- P. Blaise, N. Dos Santos, in Proceedings of the PHYTRA2 Conference, Fez (2011) [Google Scholar]
- M. Bruet et al., in Proceedings of the Four European Conference ENC 86, Geneva (1986) [Google Scholar]
- D. Bernard, A. Santamarina, Ann. Nucl. Eng. 87, 1 (2016) [CrossRef] [Google Scholar]
- F. Jatuff, G. Perret, M. Murphy, P. Grimm, R. Seiler, R. Chawla, in Proceedings of International Conference on the Physics of Reactors, Interlaken, Switzerland (2008) [Google Scholar]
- G. Perret, M.F. Murphy, F. Jatuff, Nucl. Sci. Eng. 163, 1 (2009) [Google Scholar]
- J.-Ch. Sublet et al., Nuclear Energy Agency Document No. JEF/DOC-1210, 2007 [Google Scholar]
- J.C. Chow, F.P. Adams et al., CNL Nucl. Rev. 1, 1 (2012) [Google Scholar]
- P. Leconte, J. Di-Salvo, M. Antony et al., in Proceedings of the PHYSOR2012 Conference, Knoxville (2012) [Google Scholar]
- S.C. van der Marck, Nucl. Data Sheet 113, 2935 (2012) [Google Scholar]
- G. Cacuci, in Handbook of Nuclear Engineering, edited by G. Cacuci (Springer, Berlin, 2010) [CrossRef] [Google Scholar]
- L. Mercatali, K. Ivanov, V.H. Sanchez, Sci. Technol. Nucl. Install. 2013, 573697 (2013) [CrossRef] [Google Scholar]
- A. Guglielmelli, Thesis for the second level post-graduate course in Design and Management of Advanced Nuclear Systems, University of Bologna, 2009 [Google Scholar]
- B.T. Rearden, M.A. Jessee, Oak Ridge National Laboratory Report ORNL/TM-2005/39, Oak Ridge, 2016 [Google Scholar]
- B.T. Rearden, M.L. Williams, M.A. Jessee, D.E. Mueller, D.A. Wiarda, Nucl. Technol. 174, 236 (2011) [CrossRef] [Google Scholar]
- M.L. Williams, B.T. Rearden, Nucl. Data Sheet 109, 2796 (2008) [CrossRef] [Google Scholar]
- U.S. EPR Final Safety Analysis Report, Cap. 4.3 – Nuclear Design [Google Scholar]
- U.K. EPR Pre-Construction Safety Report (PCSR), Cap. 4 – Reactor and Core Design, Subchapter 4.3 Nuclear Design [Google Scholar]
- S. Lo Meo, C. Massimi, F. Rocchi et al., Measurement of the neutron capture cross section for 155Gd and 157Gd for Nuclear Technology, European Organization For Nuclear Research (CERN), Proposal to the ISOLDE and Neutron Time-of-Flight Committee, 2015 [Google Scholar]
Cite this article as: Federico Rocchi, Antonio Guglielmelli, Donato Maurizio Castelluccio, Cristian Massimi, Reassessment of gadolinium odd isotopes neutron cross sections: scientific motivations and sensitivity-uncertainty analysis on LWR fuel assembly criticality calculations, EPJ Nuclear Sci. Technol. 3, 21 (2017)
All Tables
List of evaluations of 157Gd thermal capture cross sections as reported in scientific literature.
Contributions to overall uncertainty in criticality eigenvalue for the GE10×10-8 FA.
All Figures
 |
Fig. 1 Relative standard deviation of 155Gd and 157Gd capture cross sections. |
| In the text | |
 |
Fig. 2 U.K. EPR FA, enr. 5.0% @ 24 Gd fuel pins (left); U.S. EPR FA, enr. 3.25% @ 16 Gd fuel pins (center); U.K. EPR FA, enr. 3.2% @ 20 Gd fuel pins (right). |
| In the text | |
 |
Fig. 3 GE BWR 10×10-8 @ 14 Gd fuel pins (left); GE BWR FA 9×9-7 @ 12 Gd fuel pins (center); GE BWR 7×7 @ 6 Gd fuel pins (right). |
| In the text | |
 |
Fig. 4 Profiles of sensitivity per unit of lethargy about 157Gd(n,γ) cross section as a function of incident neutron energy for the GE10×10-8 FA; the two curves refer to different moderator densities. |
| In the text | |
 |
Fig. 5 Critical fluxes per unit lethargy for the BWR GE10×10-8 FA for three different moderator densities. |
| In the text | |
 |
Fig. 6 Effect of number of gadolinium fuel pins on the sensitivity profile. |
| In the text | |
 |
Fig. 7 Critical fluxes per unit lethargy for the BWR Peach Bottom 7×7 FA for 2, 4 and 6 gadolinium fuel pins. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


