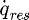| Issue |
EPJ Nuclear Sci. Technol.
Volume 3, 2017
|
|
|---|---|---|
| Article Number | 20 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/epjn/2016007 | |
| Published online | 23 June 2017 | |
https://doi.org/10.1051/epjn/2016007
Regular Article
A simplified geometrical model for transient corium propagation in core for LWR with heavy reflector
CEA/DEN/CAD/DTN/SMTA/LPMA, CEA Cadarache, 13108 Saint-Paul-lez-Durance Cedex, France
⁎ e-mail: laurent.saas@cea.fr
Received:
6
May
2015
Received in final form:
16
December
2015
Accepted:
28
January
2016
Published online: 23 June 2017
In the context of the simulation of the Severe Accidents (SA) in Light Water Reactors (LWR), we are interested on the in-core corium pool propagation transient in order to evaluate the corium relocation in the vessel lower head. The goal is to characterize the corium and debris flows from the core to accurately evaluate the corium pool propagation transient in the lower head and so the associated risk of vessel failure. In the case of LWR with heavy reflector, to evaluate the corium relocation into the lower head, we have to study the risk associated with focusing effect and the possibility to stabilize laterally the corium in core with a flooded down-comer. It is necessary to characterize the core degradation and the stratification of the corium pool that is formed in core. We assume that the core degradation until the corium pool formation and the corium pool propagation could be modeled separately. In this document, we present a simplified geometrical model (0D model) for the in-core corium propagation transient. A degraded core with a formed corium pool is used as an initial state. This state can be obtained from a simulation computed with an integral code. This model does not use a grid for the core as integral codes do. Geometrical shapes and 0D models are associated with the corium pool and the other components of the degraded core (debris, heavy reflector, core plate…). During the transient, these shapes evolve taking into account the thermal and stratification behavior of the corium pool and the melting of the core surrounding components. Some results corresponding to the corium pool propagation in core transients obtained with this model on a LWR with a heavy reflector are given and compared to grid approach of the integral codes MAAP4.
© L. Saas et al., published by EDP Sciences, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In the context of Light Water Reactors (LWR) Severe Accidents (SA) analysis and management strategies evaluation, a key element is the phenomenology associated with a corium pool that can be formed after the loss of the primary coolant and the induced core degradation. For instance, for an “in-vessel retention” (IVR) safety approach [1], where the second barrier (i.e. the vessel) is intended to contain the corium, the heat flux from the corium pool to the vessel wall determines the chances of success of such a strategy by the reflooding of the reactor pit (“External Reactor Vessel Cooling” [ERVC]). The behavior of a corium pool results from the combination of two main phenomena which are thermochemistry [2,3] (phase segregation and so corium pool stratification) and thermal-hydraulics [4] (natural convection and so heat fluxes evaluation). For in-vessel corium behavior, the main risk of vessel failure is related to the so-called focusing effect [5] (in terms of lateral heat flux imposed to the vessel wall) due to a “thin” light metal layer on top of the corium melt during the transient pool formation.
A common practice in the IVR studies [1,6,7] is to determine the corium pool thermal load in the lower head using stationary configurations, initial corium inventory and arbitrary assumptions. This corium inventory is evaluated using integral codes which simulate core degradation such as MAAP4 [8] or MELCOR [9]. The problem with this stationary approach is that it is not a bounding situation for the vessel rupture (focusing effect). Transient corium relocation from the core to the lower head has to be taken into account especially for LWR with heavy reflector (reflector thickness to ablate, stabilization with flooded down-comer, in-core corium pool stratification). Core degradation [10–12] is a combination of complex physical phenomena (thermal-hydraulics, oxidation of core materials, loss of core geometry) which could result in the corium pool formation in core and after to its propagation and its relocation in lower head.
For numerical approach of core degradation, integral codes (MAAP4 [8], MELCOR [9] or ASTEC [13]) use Cartesian grid(s) and discretization on these grids to compute physical properties evolution of the core associated. A liquid phase corresponding to corium is represented as volume fractions or cell type on the core grid (information on the degradation state of the cell). In these codes, there is no direct representation of the corium pool in core, but only cells which are partially or totally liquid. Mass and thermal exchanges are computed between the cells of the core grid. No modelling thermochemistry at the scale of the corium pool is done. This phenomenon governs the corium pool propagation in core (heat fluxes distribution for the ablation of surrounding structures [core debris, reflector, plates…]) and the draining of corium to the lower head (relocation). For example, no focusing effect associated with the corium pool in core could be modelled which could cause an earlier corium pool relocation in lower head. For LWR with heavy reflector, another modelling issue that justifies the study of corium pool propagation in core is to know the mode of corium transfer from the core to the vessel (through reflector, or core support plate or both). It has consequences on the relocation of the corium in the lower head (instant, duration, mass, composition) and it is linked to the evaluation of focusing effect in the corium pool in core. For example, MELCOR assumes only corium relocation through the core support plate.
Once a corium pool is formed in the core, the propagation of the corium pool is mainly due to its residual power and to the melting of the debris in core (stronger coupling of thermal-hydraulics and thermochemistry than before corium pool appearance). So we assume that the core degradation [10–12] until the corium pool formation and the corium pool propagation could be modeled separately.
In this paper, we propose another approach to simulate the corium pool propagation in core at the spatial scale of the corium pool. It is based on a simplified geometrical model of the degraded core and is implanted in the PROCOR framework.
To take into account the complex physical phenomena, and to manage the high level of uncertainties and the various time and spatial scales involved during the corium pool propagation in a SA, the Commissariat à l’Énergie Atomique (CEA) has developed a coupled physical and statistical framework named PROCOR (stands for “PROpagation of CORium”). This tool is based on a simplified physical modelling and the experience gained on the LEONAR code [14]. This framework is focused only on the corium propagation: no fission products and hydrogen releases are modeled as in the integral codes [8,9,13]. The use of simplified models allows propagating the uncertainties on the data or on the modeling by using a statistical tool [15] which is based on a Monte-Carlo method.
The simplified model which is proposed in this paper computes the kinetics stratification and the natural convection associated with the corium pool. The formation of the corium pool in core is not dealt with in this paper. This model starts its computation from an initial state which is a degraded core with a corium pool surrounded by core debris. We only consider LWR with heavy reflector (GenIII Pressurized Water Reactor [PWR]). We are interested in the possible lateral stabilization of the corium pool in core in case of reflooding and on the impact of the heavy reflector melting on the corium pool stratification (molten steel mass more important than for a baffle). Section 2 is devoted to the presentation of the simplified core model. Then Section 3 presents some sensitivity results obtained with this model.
2 Description of the models
To present the simplified geometrical core model, we first describe the simplified geometry of the degraded core on which it is based. This simplified geometry comes from the observations of the TMI-Unit2 severe accident [16] and is formed by simple geometrical shapes associated with core components (Fig. 1 is an illustration of TMI-Unit2 final state).
The different 0D models that compose the simplified geometrical model are given with their different coupling (see Ref. [17] for details on some of these models). These models are 0D model associated with the core component of the simplified core geometry. To complete the presentation, we explain the geometrical evolution model which computes the consistent evolution of the shape associated with each core component. This model is the originality of this work.
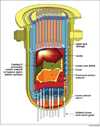 |
Fig. 1 Scheme of the lower head and core final state of the TMI-Unit2 severe accident. |
2.1 The simplified core geometry description
The simplified core geometry is composed by simple non-overlapping geometrical shapes (spherical caps, cylinders, and composition of these shapes). Each shape is associated with a degraded component of the core. The different core components are defined according to the observation of TMI-Unit 2 final state. This final state is a final state for corium pool propagation in core and relocation in the lower head. In Figure 1, corresponding to a scheme of the in-core TMI observations, a molten materials volume is surrounded by crust. A core debris volume is represented with fuel rods that seem intact. A cavity is above the core debris and the corium pool. The upper plate is damaged and the core support plate is intact. Molten materials have been retained in the baffle.
In the simplified model, from the TMI observations, we assume that the core is composed of the following degraded components: the upper plate (if it has not totally melt), the core support plate, the heavy reflector (instead of a baffle as in TMI), the corium pool (molten core materials volume), an empty volume (cavity) and the core debris (which corresponds to a porous media and represents the intact fuel rods and core debris observed in TMI). The core debris are split in two parts depending of their localization respectively to the corium pool: the lower core debris are under the top level of the corium pool and the upper core debris are above the top level of the corium pool. These core debris model the fuel rods which are in different states of degradation but not totally molten.
We assume that the simplified geometry is axisymmetric. We assume that in the core, only one corium pool can be present. When the corium pool is not present in the core (after a total draining for example), we consider that the core debris corresponds to upper debris.
The geometrical shape of a component is defined by its type and by different radii or heights to complete its description (the number of radii and heights depends on the type of the shape). The different possible types of geometrical shape are: a cylinder, a spherical cap, a truncated spherical cap, a composite shape (stack of other simple shapes), a hollow shape (which is a simple shape hollowed out by other simple shapes).
To each core component an axial position is associated (simplified geometry is assumed to be axisymmetric). This position corresponds to the level in the core. The level origin is the core support plate top surface. Figure 2 corresponds to a core geometry associated with the different core components during the in-core propagation transient.
During the corium pool propagation in core, the shape type of the corium pool could change. All the radii and heights of the core components are evolving to take into account the melting of the components and the corium pool expansion. The corium pool shape can be a composite shape (e.g. formed by several simple shapes) that evolves during its propagation. The shape numbers of the corium pool is equal to the number of the core components which are in contact with it (one corium pool shape for one core component). The corium pool shape in front of the lower debris bed is always a spherical cap or a truncated spherical cap (in case of contact with the core support plate) and on top of it a cylinder could be added if the corium pool is in contact with the heavy reflector. The types of the other core components shapes are fixed. These shapes are cylinders (core and upper plates and upper core debris) except for the lower core debris and for the heavy reflector. The lower core debris shape is a cylinder that is hollowed by the corium pool (spherical cap or truncated spherical cap). The heavy reflector is a cylinder and is hollowed by the other core components. The heavy reflector is the only component of the core that is meshed in order to accurately compute its ablation and the level of its rupture.
To simplify the geometrical core evolution, we distinguish three types of core components depending on their geometrical evolution:
the corium pool which is expanded;
the lateral core components, that can be hollowed by the corium pool: lower core debris, reflector, core support plate;
the upper core components, that are cylinder above the corium pool: the upper plate and the upper debris.
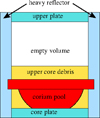 |
Fig. 2 A simplified core geometry for the corium pool propagation in core. All the core components are presented (upper plate, core support plate, lower and upper core debris, heavy reflector, corium pool [2 shapes], and empty volume). |
2.2 The in-core corium pool propagation model
Starting from an initial degraded core with a formed corium pool surrounded by debris, the corium pool propagation model computes the transient in core and the relocation of the corium into the lower head.
Physical and geometrical properties are associated with all the different components of the core. Temperature, species composition and mass are computed for each component. Their physical properties are assumed to depend on the temperature. For the lower and upper core debris and for core and upper plates, the porosity is evaluated by volume conservation. Mass and energy balance are preserved.
The simplified core geometry model is composed of several models that are time-dependent 0D models or a 1D model. These models are coupled using an explicit scheme. When it is possible, the models take the form of Ordinary Differential Equations (ODE) corresponding to conservation laws associated with the core components or with the layers of the corium pool. These different models are:
a corium pool thermal model coupled with a kinetic stratification model (see Refs. [17,18]): stratification of the corium pool evolves with added molten masses. Focusing effect phenomenon is taken into account. For each corium layer, transient mass and energy balance are computed. Heat exchange correlations are used to represent the average heat fluxes of each layer surface and heat flux profiles are used to compute local heat fluxes. On the top of the corium pool, if water is not present, a radiative heat transfer condition is used and if water is present, a temperature boundary condition is used with solidification of the top layer;
two debris models (one for lower core debris, the other for upper core debris). They compute the cooling (if water is present) and heating/melting of debris (melting due to the internal power and to contact with the corium pool). For the cooling, a debris cooling correlation is used and for the heating/melting, a transient mass and energy balance is used;
a geometrical model of the propagation: it makes the geometrical shapes of the core components consistently evolve with the melting of core components and with the corium pool expansion phenomena. It is consistent with the volume and mass balance. We assume that the corium pool expansion is driven by the local heat fluxes and is anisotropic. It determines the splitting of the core debris in lower and upper part and adjusts their porosity to ensure volume conservation. This model is detailed in the next subsection;
a model for the heavy reflector ablation. An axial grid is used to discretize the heavy reflector. A simplified 1D fusion front model is used for each 1D slab of the reflector. If water is present in the down-comer, a critical heat flux correlation is used and established thermal conduction is assumed. If there is no water, we use an adiabatic fusion front. Reflector ruptures occur when the residual thickness of a 1D slab is lower than a thickness threshold. We use the axisymmetric surface of contact between the corium pool and the heavy reflector to compute the ablation, but we assume that the rupture is localized;
a model for the upper plate ablation. This model corresponds to a 0D model of mass and energy balance;
a corium draining and fragmentation model for the corium relocation into the lower head when reflector failure occurs. This model is based on a jet break up length correlation and it determines the liquid and debris corium that relocate in the lower head;
a model to manage water mass and level in case of reflooding (water evaporation due to core debris cooling or corium fragmentation).
At the present time, we assume that residual water is present in the vessel lower head and consequently that the core support plate does not melt and break (lower head residual water level is assumed to correspond to the upper level of the core support plate). For all 0D models for exchange surfaces, the geometrical surfaces of the simplified core geometry presented before are used (axisymmetric geometry). The volume of a core component corresponds to its geometrical volume in the simplified core geometry.
These different models are coupled to form the simplified core geometry model for the transient propagation. Each 0D model which corresponds to ODE system has its own local integration time step and a fixed macro time step Δt is used to perform the synchronization between the different models. During a macro time step, the corium pool propagation in core is computed using the following steps:
evaluation of water level and mass with evaporation due to corium relocation or core debris cooling;
evaluation of the contact surfaces and heat fluxes for the corium pool to the other core components. The corium pool stratification and heat flux profiles are taken into account;
computation of the heating/melting of core components (lower and upper core debris, heavy reflector, upper plate and core support plate) using the corium pool heat flux;
if reflector failure occurs, evaluation of the corium relocating in the lower head;
computation of the corium pool expansion and the core geometry evolution by taking into account the molten materials;
evaluation of stratification and heat fluxes of the corium pool;
update of the core geometry after corium pool stratification evaluation (density and mass of the corium layers may have changed and consequently the total volume of the corium pool).
In the following subsection, we will focus on the corium pool expansion and the core components geometry evolution algorithms.
2.3 The geometrical evolution model
This model computes and updates the core components geometry during the transient taking into account the mass flow rates of molten core components and the mass flow rates of corium pool draining (in the reflector failure case). It is based on a core mass and volume balance. The total mass and total volume of the different core components are conserved during the geometry evolution due to corium pool propagation. For each core component, the shape and axial position evolution are computed. For the lower and upper core debris, a mass and volume transfer may occur because of the evolution of the corium pool top level and of their definitions. The upper and lower core debris are defined with respect to the corium pool top level (corium pool position in the core) which evolves due to corium pool expansion and to mass adding from molten materials. The porosity of the upper and lower core debris may also be adjusted in this volume transfer process. The corium pool is a liquid so it is not porous while the core debris have varying porosities. The upper plate and the core plate are also porous. To conserve the volume, the empty volume increases during the transient to take into account the porosity of the core components that are molten.
The model has to manage the expansion of the corium pool shapes by taking into account anisotropic heat fluxes due to natural convection and the melting of surrounding core components. Before explaining the expansion of the corium pool shapes, we will describe the different steps of the algorithm associated with the geometrical model for a macro time step interval [t,t + Δt]:
computation of the ablated volumes of the lateral and upper core components and the new corium pool volume by mass and volume conservation;
expansion and modification of the shapes of the corium pool associated with each lateral component using the expansion coefficients and adding a new shape to the stack for the corium pool if necessary (e.g. contact with the reflector or the core support plate). The lateral component shapes are then obtained from the corium pool by hollowing out. The corium pool anisotropic expansion will be presented hereafter;
because of the porosity and the corium pool draining, the volume of the corium pool is different from the shapes hollowed out in the lateral component and computed by its expansion. The corium pool shapes are updated using the hollowed shapes and their volume (volume conservation ensured by filling the hollowed shape with the updated corium pool volume);
computation of the shapes of the lateral components from the hollowed shape and the updated corium pool shapes. During this step, mass and volume transfer between upper and lower core debris may be performed depending on the top level of the corium pool. The transfer may be in both directions depending on the evolution of the corium pool volume. Modification of the porosity of the upper and lower core debris is done in case of transfer;
computation of the shapes of the upper components using their volumes which are updated taking into account the ablation by the corium pool;
when all the different shapes have been updated, the corium pool top level is computed by volume conservation and the empty volume is increased. All the top levels of the other core components are deduced from the corium pool.
Figure 3 corresponds to the axial and radial expansions of a corium pool shape (case of lower core debris without contact with the core support plate). At the end of the paper, a nomenclature is given for the notations for all the equations. The variation of the mass and the volume of the corium pool are given by: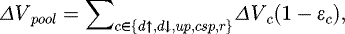 (1)
(1)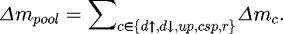 (2)
(2)
The evolution of the corium pool shape of the reflector is given by the 1D model and corresponds to an average cylinder computed from the 1D slab of the reflector grid which is ablated and still in contact with the corium pool.
For the other lateral core component (lower core debris for example), the ablation is driven by the outgoing thermal heat flux at the corium pool boundary: the local ablation velocity along the contact surface Sc between a corium pool shape and the lateral core component c is an increasing function of the local heat flux outgoing of the corium pool. Natural convection in the corium pool is responsible for the heat flux profile at the corium pool lateral shape surface. To take into account the anisotropy of the ablation between the top and the bottom of the lateral surface Sc, we define expansion coefficients (α, β) that link the axial and radial expansion of the corium pool shape. α corresponds to proportionality between lateral and axial propagation and β to a constant difference. We note Δhpool the variation of the height of the shape,  the variation of the upper radius for a truncated spherical cap or a spherical cap, and
the variation of the upper radius for a truncated spherical cap or a spherical cap, and  the variation of the lower radius of a truncated spherical cap (
the variation of the lower radius of a truncated spherical cap (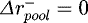 for a spherical cap). The variation of the volume of the corium pool shape is a fixed analytical formula depending on the shape type (deduced from classical geometry formula for a spherical cap or truncated spherical cap):
for a spherical cap). The variation of the volume of the corium pool shape is a fixed analytical formula depending on the shape type (deduced from classical geometry formula for a spherical cap or truncated spherical cap):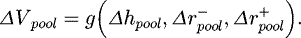 (3)
(3)
For a spherical cap, the expansion coefficients determine the shape modification by the following relation: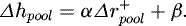 (4)
(4)
For a truncated spherical cap, the expansion of the corium pool shape is given by (height is fixed 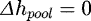 because it corresponds to lateral ablation with the corium pool in contact with the core support plate):
because it corresponds to lateral ablation with the corium pool in contact with the core support plate):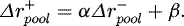 (5)
(5)
We assume that these coefficients are function of local heat fluxes at the bottom 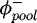 (at bottom level
(at bottom level 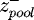 of the pool) and the top
of the pool) and the top  (at top level
(at top level 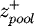 of the pool) of the lateral surface Sc of the component associated corium pool shape. The heat fluxes are calculated from the corium pool layer average lateral heat fluxes
of the pool) of the lateral surface Sc of the component associated corium pool shape. The heat fluxes are calculated from the corium pool layer average lateral heat fluxes 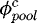 (from the thermal balance of each corium pool layer as calculated by corium pool model) and the layer heat flux profiles (the profile is defined by a function f(z) of the level z and is given for each corium pool layer):
(from the thermal balance of each corium pool layer as calculated by corium pool model) and the layer heat flux profiles (the profile is defined by a function f(z) of the level z and is given for each corium pool layer):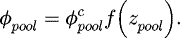 (6)
(6)
From equations (1), (3) and (4) or (5) with known expansion coefficients (α, β), we can compute from the volume variation the corium pool shape variation 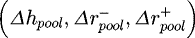 and consequently the new shape for the corium pool.
and consequently the new shape for the corium pool.
We propose two arbitrary choices to differentiate the axial and radial expansions by determining the expansion coefficients from the corium pool heat fluxes. These choices are linked to a simple adiabatic 1D fusion front model for a material (in the next formula, the “c” component) which is ablated by a heat flux from the corium pool 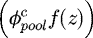 . The local ablation speed associated with the fusion front can be expressed from the material physical properties and the corium pool heat flux:
. The local ablation speed associated with the fusion front can be expressed from the material physical properties and the corium pool heat flux: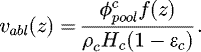 (7)
(7)
The two choices for the expansion coefficients are:
the ratio of the ablation velocity on the top and bottom of the corium pool shape (called “Ratio” option, the shape deformation is proportional to the local ablation speed):
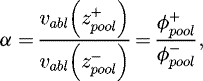 (8)
(8) (9)
(9)the difference of ablation velocity of the lateral ablated component c on the top and bottom of the associated corium pool shape (called “Sum” option):
 (10)
(10)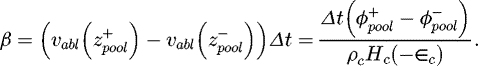 (11)
(11)
When the expansion of each shape of the corium pool associated with each lateral component has been calculated, the shape may be “cut” radially or axially (preserving its volume) if it overlaps with the boundary of the associated lateral core component shape. This “cutting” operation may create a new corium pool shape which will be in contact with another lateral component. For instance, when the corium pool propagates into the lower debris, it will eventually reach the reflector wall and be in contact with it with this mechanism. The contact may occur during a time step but is detected only at the end of this time step for the moment (explicit scheme). Then a cylindrical shape is added for the corium pool shapes for the contact with the reflector.
Once the corium pool shapes are calculated from ablation, the corium pool mass is used to resize the top corium pool shape: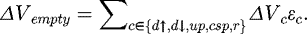 (12)
(12)
The difference of core component ablated material volume and the molten material volume due to porosity corresponds to the evolution of the empty volume. From this empty volume, all the positions of the core components are computed.
 |
Fig. 3 Radial and axial expansion of a spherical cap associated with the corium pool. |
3 First results
In this section, we give some results obtained for a GenIII PWR with our simplified geometrical model for transient propagation in core. As we have previously mentioned, our model needs an initial state which corresponds to a degraded core with a corium pool (total core degradation). This initial state can be obtained from an integral code. In this present paper, we use the MAAP4 code.
Figure 4 is an example of core geometry that can be observed during the in-core corium pool propagation transient. In this picture, the corium pool is stratified (a heavy metal layer and oxide layer surrounded by crust and a steel layer above). The corium pool is in contact with the lower core debris (spherical cap) and with the reflector (cylinder). The ablation of the reflector is not shown (1D axial grid).
In this section, a first part corresponds to a short study on the sensitivity to the initial core state. We explain how the initial state is computed and present a parametric study with respect to a temperature parameter and the initial time. Because the goal of our simplified model is to introduce a modelling at the scale of the corium pool, the second part is dedicated to the sensitivity of the model parameters for the in-core propagation transient: the arbitrary expansion coefficients and other parameters associated with the corium pool stratification and thermal-hydraulics are studied. This first sensitivity analysis has to be completed with more computations and with uncertainties analysis. In this paper, we use only one MAAP4 computations to test our model and to make comparisons.
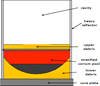 |
Fig. 4 Example of corium pool propagation in core computed with the simplified geometrical model in the PROCOR framework (computation results). The corium pool is stratified: the layers from bottom to top are: a heavy metal layer (m = 20,875 kg, T = 3090 K), an oxidic layer (m = 70,389 kg, T = 3139 K), a steel layer (m = 571 kg, T = 2219 K). The corium pool shape is formed by a spherical cap and a cylinder. |
3.1 Initial state sensitivity
The initial core degraded state is obtained from MAAP4 computations using criteria to determine which cells correspond to the corium pool. We assume that the cells containing corium are cells that are totally liquid (variable IGTYP equal to 5) or the cells that have a temperature (variable TNOD) above a corium pool threshold temperature Tliquidus (corresponds to a liquidus temperature for the pool). We assume that all the fuel rods cells that are not part of the corium pool correspond to core debris. The mass and temperature of all the core components are computed by mass and energy conservation. The mass is obtained by globalization of the variable MNOD. For the temperature, we assume no phase transition and constant specific heat, so temperature is obtained by globalization of TNOD with ponderation with MNOD. The species compositions are computed by a global inventory of the initial composition and assuming that the extra mass corresponds to zirconium oxidation. The steel components have constant composition and we assume that the corium pool and the core debris have the same composition. Two initial times with associated initial core degraded states can be defined:
the time of the appearance of the corium pool (referred as “Appear” in the remainder);
the time of the contact of the corium pool with the heavy reflector (“Contact”).
To study the initial state sensitivity, we compare the corium propagation at different moments for different values of the liquidus temperature Tliquidus and for the two initial times. These results are also compared with MAAP4 computation from which the initial time and state are deduced. The reactor is GenIII PWR with heavy reflector and the scenario corresponds to a LOOP650 (Loss Of Offsite Power with loss of all the diesel supplies).
The MAAP4 results are summarized in Table 1 for Tliquidus = 3000 K. The upper plate disappears at 17,800 s. The masses of the corium pool, lower core debris and upper core debris in Table 1 correspond to the mass evaluated from the MAAP4 results in the same way as the initial state (same processing to compute the mass of the different core components). This mass is used for the comparison with our model. The reflector rupture occurs at 24,603 s and the level of 1,65 m from the top of the core support plate. Then a lateral draining through the hole of the heavy reflector occurs and stops at 24,603 s. The diameter of the hole is one mesh and its diameter is 0.14 m. The lateral drained mass from the core to the lower head is 126,707 kg. After the lateral draining, the corium flows through the core support plate. The core support plate disappears at 29,503 s (100 s after the corium pool contact), and a massive axial draining through the core support plate occurs.
We compare the MAAP4 results with the results of our model using different initial conditions: the temperature of liquidus Tliquidus and the initial time. In Table 2, the time of the initial state, of the first reflector rupture and of the core support plate contact are given (for the moment no corium draining through the plate is modelled). For the first reflector rupture we also give the level of the hole. The corium pool, lower and upper core debris masses are given with the time corresponding to the event in Table 3. Until the starting time is reached, the results correspond to the processed results of MAAP4. For all cases, two ruptures of the heavy reflector can be observed. Figure 5 presents the variation of the thickness of the reflector with the time. The reflector ruptures occur each time by focusing effect. At the reflector ruptures, the corium pool is composed from bottom to top by: a heavy metal layer and an oxidic layer surrounded by a crust and a steel layer above. The steel layer corresponds to the ablated steel of the reflector.
Table 3 gives the corium pool layer masses and the lower and upper core debris masses for the different cases at the reflector rupture time. The steel layer which is responsible for the focusing effect is very thin and consequently the rupture of the reflector is very fast. For the moment, the model that we use for evaluating the focusing effect overestimates the lateral heat flux for very thin layers [19] and the fusion front model of the reflector does not take into account the transient conduction in the reflector (overestimation of the speed of ablation).
Compared to MAAP4, the melting of the reflector is faster and the difference of the corium pool is essentially due to the molten steel of the reflector. Another difference is the influence of the liquidus temperature Tliquidus on the masses of the lower and upper core debris which explains the level of the reflector first rupture. A high temperature delays the time of appearance of the corium pool or contact with the reflector. It corresponds to a corium pool which is on the top of the degraded core and so the rupture is at high level. For a lower temperature, the corium pool is more in the middle of the core debris and the rupture occurs at a lower level.
MAAP4 results (analyzed as initial state).
Sensitivity to initial state (temperature and initial time).
Sensitivity to initial state (masses of pool layers and debris).
 |
Fig. 5 Variation of the reflector thickness (in m) depending on the level (in m) from the core support plate and during time (in s). Two reflector ruptures occur (first at 2.26 m and second at 0.5 m). |
3.2 Model parameter sensitivity
The model parameters that we study here are the arbitrary choice of the expansion coefficients (“Ratio” or “Sum”). We use the “case 2” of the previous sensitivity analysis to have a more important corium pool propagation in the core (the corium pool which is more in the top of the core debris and with an initial state which corresponds to the corium pool appearance). We change also some parameters associated with the corium pool model. The case A corresponds to the “Ratio” expansion coefficients and the case B to the “Sum”. For the same initial state, the reflector rupture in the case A occurs at 21,343 s at the level 2.28 m and for the case B at 21,943 s at level 2.25 m. The radial propagation is slower for the “Sum” expansion coefficients and consequently the corium pool at the reflector melting is bigger. The shape of the corium pool looks more like a hemisphere. Table 4 gives the masses of the different layers of the corium pool and of the lower and upper debris.
Sensitivity to parameters for the simplified geometrical model.
4 Conclusions
In this paper, we propose and use a new simplified geometrical model to compute the corium pool propagation in core. This model can only be used once a corium pool has appeared in the degraded core. It simulates the in-core corium pool propagation transient and will permit to characterize the mode of corium transfer from the core to the vessel. The initial state of the degraded core has to be computed separately. A short sensitivity analysis has been performed on this model and a first comparison with the integral code MAAP4 has been done. The models associated with the rupture of the reflector have to be improved (heat flux from the corium pool [19] and fusion front for the reflector). The assumption on the non-ablation and non-rupture of the core support plate due to the presence of residual water in the lower head has to be studied and a model for the core support plate may be developed, for example when no water is present (evaporation of the residual water due to corium flow from the core to the lower head).
The sensitivity analysis and comparison with integral codes have to be completed and an uncertainties analysis on the initial state of the degraded core and on the corium pool propagation model parameters has to be performed with the PROCOR framework. The goal of the uncertainties analysis could be the evaluation of the relocation of the corium and the debris into the lower head in order to perform a more accurate and realistic evaluation of the vessel failure by taking into account transient phenomena.
Acknowledgments
This work has been carried out within the framework of the PROCOR platform development funded by CEA, EDF and AREVA. The MAAP4 computations used for the initial state and for the comparison have been performed by EDF and AREVA NP.
Nomenclature
To distinguish the different core components, we use the following subscripts: “pool” for the corium pool, “d↑” for the upper core debris, “d↓” for the lower core debris, “up” for the upper plate, “csp” for the core support plate, “r” for the reflector and “empty” for the empty volume.
ΔVc: variation of volume of a component c
Δmc: variation of mass of a component c
ε c : porosity of a component c
ρ c : density of a component c
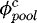 :
average corium pool heat flux on component c
:
average corium pool heat flux on component c
H c : fusion enthalpy of component c
References
- T.G. Theofanous, C. Liu, S. Addition, S. Angelini, O. Kymalainen, T. Salimassi, In-vessel coolability and retention of a core melt, Nucl. Eng. Des. 169, 1 (1997) [CrossRef] [Google Scholar]
- M. Fischer, P. Levi, G. Langrock, A.A. Sulatsky, E.V. Krushinov, The impact of thermal chemical phenomena on the heat fluxes into the RPV during in-vessel melt retention, in Proceedings of Int. Congress on Advances in Nuclear Power Plants ICAPP 2011, Nice, France (2011) [Google Scholar]
- D.F. Tsurikov, V.F. Strizhov, S.V. Bechta, V.N. Zagriazkin, N.P. Kiselev, Main results of MASCA1 and 2 projects Tech. rep., RRC Kurchatov Institute, 2007 [Google Scholar]
- J.M. Bonnet, J.M. Seiler, In-vessel corium pool thermal-hydraulics for bounding cases, in Proceedings of salt test expert group meeting RASPLAV seminar, Munich, Germany (2000) [Google Scholar]
- J.M. Seiler, B. Tourniaire, A phenomenological analysis of melt progression in the lower head of a pressurized water reactor, Nucl. Eng. Des. 268, 87 (2014) [CrossRef] [Google Scholar]
- H. Esmali, M. Khatib-Rahbar, Analysis of likelihood of lower head failure and ex-vessel fuel coolant interaction energetics for AP1000, Nucl. Eng. Des. 235, 1583 (2005) [CrossRef] [Google Scholar]
- J.L. Rempe, D.L. Knudson, C.M. Allison, G.L. Thinnes, C.L. Atwood, M.J. Cebull, Potential for AP600 in-vessel retention through ex-vessel flooding, Tech. Report, INNEL/EXT-97-00779, 1997 [Google Scholar]
- Fauske Associates Inc., MAAP4 - modular accident analysis program for LWR power plants: Code structure and theory (Electric Power Research Institute, 1994), Vol. 2, Chap. 1 [Google Scholar]
- R.O. Gauntt, J.E. Cash, R.K. Cole, C.M. Erickson, L.L. Humphries, S.B. Rodriguez, M.F. Young, MELCOR computer code manual, NUREG/CR-6119, Rev. 3 (2 vols), 2005 [Google Scholar]
- T. Haste, M. Steinbruck, M. Barrachin, O. de Luze, M. Grosse, J. Stuckert, A comparison of core degradation phenomena in the CORA, QUENCH, Phébus SFD and Phébus FP experiments, Nucl. Eng. Des. 283, 1 (2015) [CrossRef] [Google Scholar]
- B.R. Sehgal et al., in Nuclear safety in light water reactors (Academic Press, Boston, 2012), pp. 89–183 [Google Scholar]
- T.J. Haste, B. Adroguer, U. Brockmeier, P. Hofmann, K. Muller, M. Pezzilli, In-vessel core degradation in LWR severe accidents ECSC-EC-EAEC (European Commission, Brussels, 1996) [Google Scholar]
- J.-P. van Dorsselaere, C. Seropian, P. Chatelard, F. Jacq, J. Fleurot, P. Giordano, N. Reinke, B. Schwinges, H.-J. Allelein, W. Luther, The ASTEC integral code for severe accident simulation, Nucl. Technol. 165, 293 (2009) [CrossRef] [Google Scholar]
- B. Tourniaire, B. Spindler, G. Ratel, J.M. Seiler, M. Iooss, B. Marqes, F. Gaudier, G. Greffier, The LEONAR code: a new tool for PSA level 2 analyses, in Proceedings of Joint OECD/NEA - EC/SARNET2 Workshop on In-Vessel Coolability, Paris, France (2009), Vol. NEA/CSNI/R(2010)11, pp. 105–121 [Google Scholar]
- F. Gaudier, URANIE: the CEA/DEN uncertainty and sensitivity platform, Proc. Soc. Behav. Sci. 2, 7660 (2010) [Google Scholar]
- J.M. Broughton, P. Kuan, D.A. Petti, E.L. Tolman, A scenario of the Three Mile Island unit 2 accident, Nucl. Technol. 87, 34 (1989) [CrossRef] [Google Scholar]
- R. Le Tellier, L. Saas, S. Bajard, Transient stratification modelling of a corium pool in a LWR vessel lower head, Nucl. Eng. Des. 287, 1 (2014) [Google Scholar]
- M. Salay, F. Fichot, Modelling of metal-oxide corium stratification in the lower plenum of a reactor vessel, in Proceedings of Int. Topical Meeting on Nuclear Thermal-Hydraulics (NURETH-11), Avignon, France (2005) [Google Scholar]
- C. Villermaux, Modélisation physique et numérique de la convection naturelle dans une couche de fluide de faible rapport d’aspect dans le cadre des études d’accidents graves de réacteurs à eau sous pression, Ph.D. Thesis, Institut National Polytechnique de Grenoble, 1999 [Google Scholar]
Cite this article as: Laurent Saas, Romain Le Tellier, Sophie Bajard, A simplified geometrical model for transient corium propagation in core for LWR with heavy reflector, EPJ Nuclear Sci. Technol. 3, 20 (2017)
All Tables
All Figures
 |
Fig. 1 Scheme of the lower head and core final state of the TMI-Unit2 severe accident. |
| In the text | |
 |
Fig. 2 A simplified core geometry for the corium pool propagation in core. All the core components are presented (upper plate, core support plate, lower and upper core debris, heavy reflector, corium pool [2 shapes], and empty volume). |
| In the text | |
 |
Fig. 3 Radial and axial expansion of a spherical cap associated with the corium pool. |
| In the text | |
 |
Fig. 4 Example of corium pool propagation in core computed with the simplified geometrical model in the PROCOR framework (computation results). The corium pool is stratified: the layers from bottom to top are: a heavy metal layer (m = 20,875 kg, T = 3090 K), an oxidic layer (m = 70,389 kg, T = 3139 K), a steel layer (m = 571 kg, T = 2219 K). The corium pool shape is formed by a spherical cap and a cylinder. |
| In the text | |
 |
Fig. 5 Variation of the reflector thickness (in m) depending on the level (in m) from the core support plate and during time (in s). Two reflector ruptures occur (first at 2.26 m and second at 0.5 m). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.