| Issue |
EPJ Nuclear Sci. Technol.
Volume 6, 2020
|
|
|---|---|---|
| Article Number | 9 | |
| Number of page(s) | 8 | |
| DOI | https://doi.org/10.1051/epjn/2020004 | |
| Published online | 08 April 2020 | |
https://doi.org/10.1051/epjn/2020004
Regular Article
Uncertainty propagation for the design study of the PETALE experimental programme in the CROCUS reactor
1
Laboratory for Reactor Physics and Systems behaviour (LRS), Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
2
Laboratory for Reactor Physics and Thermal Hydraulics (LRT), Paul Scherrer Institut (PSI), 5232 Villigen, Switzerland
3
Nuclear Energy and Safety Research Division (NES), Paul Scherrer Institut (PSI), 5232 Villigen, Switzerland
* e-mail: laureau.axel@gmail.com
Received:
2
September
2019
Accepted:
16
January
2020
Published online: 8 April 2020
The PETALE experimental programme in the CROCUS reactor intends to provide integral measurements to constrain stainless steel nuclear data. This article presents the tools and the methodology developed to design and optimize the experiments, and its operating principle. Two acceleration techniques have been implemented in the Serpent2 code to perform a Total Monte Carlo uncertainty propagation using variance reduction and correlated sampling technique. Their application to the estimation of the expected reaction rates in dosimeters is also discussed, together with the estimation of the impact of the nuisance parameters of aluminium used in the experiment structures.
© A. Laureau et al., published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Numerous integral experiments intend to improve the knowledge on the nuclear data and their associated uncertainty. Such experiments can be employed to validate the present nuclear data libraries and numerical codes, or can be used to improve the nuclear data libraries via assimilation techniques. In this frame, the present work is related to the PETALE experimental programme [1,2] during its design phase. This programme aims at providing better constraints on the neutron cross sections in heavy reflectors for water reactors such as the European Pressurized Reactor (EPR) [3,4]. It consists in a reactivity worth and a neutron transmission experiment in the CROCUS reactor. A stack of thick (2 cm) metal plates interleaved with neutron detectors in the reflector. These detectors consist of thin activation foils (<mm) of several materials in order to use different reactions to be sensitive to different parts of the neutron spectrum. Specific numerical developments have been required and are detailed in the twin article [5] to perform the propagation of nuclear data uncertainty on this kind of system.
As an illustration, the 56Fe total cross section uncertainty is represented in Figure 1 as the dispersion between random ACE files from the TENDL library [6]. The discrepancy between these different random files is of around 5–30% at high energy (bottom-right), and may be locally very important near resonances due to the uncertainty on the energy position of these resonances (middle).
In order to optimize the capability of the PETALE experimental programme to provide useful information, the general objective is to maximize the uncertainty propagation of the reflector plate cross sections on the reaction rates in the foils. At the same time, the objective is to minimize the impact of the uncertainties due to all the other elements: e.g. fuel/water cross sections, core and experiment geometry, composition. Achieving a measurement with an accuracy better than the prior uncertainty will ensure that PETALE can provide new constraints and that the posterior uncertainty after the assimilation process will be reduced. From the prior uncertainty propagation, an estimation of the required precision on the measurement of the reaction rates in the foils will also be obtained.
Section 2 is devoted to the description of the experimental setup and its implementation in the Serpent2 Monte Carlo calculation code [7]. Section 3 then describes the variance reduction method developed to manage the low probability that a neutron coming from the core reaches the foils in the reflector. Finally, the nuclear data uncertainty propagation with a correlated sampling approach is presented in Section 4 to estimate the target uncertainties to provide feedback on the nuclear data.
 |
Fig. 1 56 Fe cross-section selected randomly form ACE files of the TENDL2017 nuclear database (left) with a zoom on the first resonance (middle) and in the high energy (right) regions. The first ACE file (in red in the upper row) has been used as reference and the variation between this file and 32 versions of this cross section is displayed in the lower row. |
2 Description of the experimental setup
2.1 Description of the CROCUS reactor
The CROCUS reactor represented in Figure 2 is a zero power light water reactor operated at Ecole Polytechnique Fédérale de Lausanne (EPFL) for teaching and research activities [1]. It is composed of two interlocked fuel zones, with oxide uranium enriched at 1.806% in the inner zone and metal uranium enriched at 0.947% at the periphery. The maximum authorized power is 100 W. More information on CROCUS is available in [8,9].
2.2 Description of the PETALE experimental programme
As already mentioned, the PETALE experimental programme aims at providing reactivity worth and a precise characterisation of the neutron flux amplitude and spectral variation in a heavy reflector materials. The in-core device allows up to eight successive thick metal plates of 2 × 30× 30 cm3 interleaved with nine thin foils (dosimeters), one between each plate and two at the endpoints of the device. The plates are surrounded by a hoistable waterproof aluminium box. The foils are extracted for an activity measurement using a High Purity Germanium (HPGe) detection system in the reactor hall for dosimeters with a short lifetime.
The measured activities in the different foils will characterise the attenuation of the neutron flux. Associated to various foil compositions (Au, Ag, In, etc.) and then different cross sections (see Fig. 3), the experiment will be sensitive to different parts of the neutron spectrum. In this article, we focus on the example of indium foils for which two pieces of information are available: the capture and the inelastic reactions. Both reactions induce the emission of specific gamma ray emissions: the former provides feedback mainly in the thermal range, whereas the latter is sensitive to the fast range only.
A first parametric study [2] performed with the MCNP code [10] has shown that the dimension of the plates can be limited to 30 × 30 cm2 with acceptable border effects. In order to obtain precise data for the different isotopes composing a heavy reflector, the measurements will be repeated for different plate compositions: Fe, Ni, Cr, and steel. In this paper, the results presented have been computed with the iron plate composition associated to the indium foils to illustrate the methodology and discuss the results obtained. Further studies will be performed with all the other configurations.
Figure 4 presents the neutron flux with a linear scale in CROCUS and the heavy reflector plates of the PETALE setup in the upper left region. A different pattern is observed between the thermal and fast ranges. As expected, the fast neutrons (bottom-right) are very concentrated at the core center, and the pin positions are observed in this case through the maximum spots obtained. One can see that an important number of fast neutrons go through the metal reflector due to the larger slowing down area of iron compared to water. Concerning the thermal neutrons (top-right), the pins are directly visible through the local flux reduction. The strong flux depletion in the reflector area is already noticeable for this range of energy due to the neutron reflection and absorption in iron. It is interesting to note that the thermal neutron population is larger in the water behind the experiment due to the fast neutrons that propagate through the iron and are finally thermalised there.
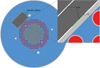 |
Fig. 2 Axial section of CROCUS represented using the Serpent2 code, with the addition of the PETALE metal reflector (top-left). The oxide uranium fuel is displayed in orange, the metal uranium fuel in red, and the water in blue. The four circles in the water reflector are fission and ionisation chambers used as CROCUS monitors. A zoom on the interface between CROCUS and the metal reflector shows the first foil with a width multiplied by 10 in order to be visible (1 g of indium for the first foil instead of 0.1 g). |
 |
Fig. 3 Cross section of interest of different foil compositions. |
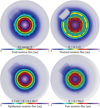 |
Fig. 4 Radial neutron flux in linear scale for different ranges: total (top-left), thermal (top-right), epithermal (bottom-left) and fast (bottom-right). The axial position used to score the flux corresponds to a 10 cm width gate centered around the PETALE device. |
3 Variance reduction in the metal reflector
In order to estimate the absorption rate inside the foils located in the metal reflector, a variance reduction is required in order to increase the number of thermal neutrons simulated in the metal reflector plates. This work has been performed with a modified version of Serpent2 code v2.1.21 used for previous studies [11] and where the correlated sampling technique has been implemented [12,13]. Even if some variance reduction methods have already been implemented in recent developments [14] of Serpent2, a specific variance reduction has been developed in this work dedicated to applications for detectors near to a reactor with specifictreatments according to the neutron energy. Different approaches exist, for example using weight windows [15] and adjoint flux [16] to drive the neutrons on a path leading to the detectors. However in this work the main target is the uncertainty propagation. The variance reduction is a mandatory step but not the final objective. For this reason a more straightforward approach has been developed here whose algorithm can be improved in a future work.
3.1 Observables and figure of merit
The final parameters of interest in this study are the reaction rates in the foils. As already detailed, several foil materials will be used, characterised by different absorption or inelastic cross sections, and sensitive to different parts of the neutron spectrum. To avoid being specific to a foil composition, we have developed a generic variance reduction method with an optimisation on the whole neutron spectrum in the different foils and not on a specific reaction rate.
In orderto check the implementation of this algorithm, an analog reference solution is calculated without any variance reduction using a classic Serpent2 calculation. Combining this reference and the result of the calculation with the variance reduction, two results are considered:
-
The residual: difference between the biased and the reference flux in the lethargy bin, expressed in number of standard deviations (σ). The quadratic sum of the statistical uncertainties are expected to be between ± 1 at ~68% as a quality check.
-
The figure of merit (FOM): quantification of the ‘improvement’ provided by the variance reduction. Since the variance σ2 decreases with the simulation time t, then
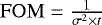 is constant and proportional to the number of events useful for the detector. Finally, the FOM ratio between the reduced variance and the reference calculation is considered (large values being better).
is constant and proportional to the number of events useful for the detector. Finally, the FOM ratio between the reduced variance and the reference calculation is considered (large values being better).
The two methods applied and detailed below are directly adjusted by ‘trial and error’ runs with short calculations. For this purpose, additionally to the FOM and to the classic flux-map as represented in Figure 4, a twin map called a raw flux map is generated without the neutron weighting in the score process. For a classic neutron weighted flux score, the summed quantity for each neutron is the travelled distance multiplied by the neutron weight (normalised by the sum of the absorptions); in this raw flux, the neutron travelled distance is thus not normalised by the neutron weight. This second map provides useful information complementary to the FOM to answer the question ‘where does the simulation spend time?’, the objective being to concentrate the neutrons close to the detectors. In order to compare these calculations, each result presented in this Section 3 has been performed using a 10-hour calculation on an Intel Xeon 2.2 GHz×24 cores.
3.2 Biasing methods
3.2.1 Biasing of the neutron source distribution
The first implemented method concerns the fission distribution in the core, the general idea being to produce more fissions near the experiment setup and then optimise the variance reduction. Instead of creating the neutrons with a distribution corresponding to the real distribution of the fissions in the reactor, the fission neutrons are preferentially created close to the metal reflector. To do so, the fission neutron production rate is artificially increased near the position of the experiment, and the created neutrons get a lower weight accordingly. This distribution is provided by the user with two arguments: a specific position (here the metal reflector) and a ratio (2% here). Then the distribution of the neutron source amplification is 1 near to the reference position followed by an exponential decrease down to 2% at the furthest position of fuel in the core. The maximum distance is determined on the fly during the calculation through the occurring fission events. The ratio is taken large enough to allow some of the neutrons to reach this portion of space, in the opposite case the convergence of global estimate would be too slow (such as the keff or the average energy released by fission per source neutron).
3.2.2 Biasing based on the hit-distance to target
The second approach is a neutron biasing based on neutron splitting with a duplication in n-neutrons with the same properties (position, energy, etc.) and a conservation of the total weight. A weight map has to be provided or estimated by the Monte Carlo code. A possible importance map is the adjoint flux, the latter coming from a deterministic neutron calculation or from the Monte Carlo calculation. As previously mentioned, the variance reduction is a mandatory step but not the final objective. For this reason a straightforward approach has been developed here.
The importance map used here is provided by the Monte Carlo calculation itself. The algorithm is based on a progressive learning of the minimum number of hits required to reach the target (the foils). When a neutron is coming from any position and reaches a foil, then the weight map is modified by learning that the previous position is at 1 hit from the target. And iteratively, when another neutron reaches this intermediate position, the distance is set to + 1 and so on. Finally, the whole space has a weight corresponding to the distance to the target.
Note that for this approach, the weight map is progressively built during the calculation. The user only has to provide a maximal weight for the targets (the foils here), this weight being adjusted after a few calculation iterations. For the closest foil the weight is set to 25, and 29.8 for the furthest one (+ 0.6 per foil).
3.2.3 Results
The following results use both neutron source distribution and hit-distance approaches. The weight field is discretized in space (250 × 250 × 250 bins) and energy (12 lethargy bins – one per decade). There is no angular discretisation yet, although this feature would be interesting for a better biasing of the fast neutrons. The map field is represented in Figure 5 with the obtained flux in the reactor.
The weight map (first line of Fig. 5) show that the fast component (right) travels a larger distance than the thermal one (left). Note that the thermal weight increases on the boundary of the metal reflector. This is due to the thermal neutrons that might reach the foils in a very limited number of hits with a streaming effect between the metal plates.
The raw flux maps (lines 2 and 3) show that the amount of simulated neutrons is much larger near the experiment. Fast neutrons arefocused in the foil direction. Compared to the weighted flux (real flux), the amount of thermal neutrons is two orders of magnitude larger (orange versus light blue).
Thanks to the larger number of neutrons simulated in the region of interest, a better statistical convergence is obtained as illustrated in Figure 6. This figure presents the reference (no variance reduction) and the optimised neutron spectra, together with the residual and the FOM. The impact of the variance reduction method is directly visible by comparing the two first plots of Figure 6. The residual showed for all the different volumes is centered around zero. The fraction of events located out of ± 1 σ is equal to 65% for the energies larger than 0.03 meV, meaning that the results are normally distributed (68% expected for a pure statistical noise). In the energy range below 0.03 meV (under the thermal peak), the fraction of events out of ± 1 σ is around 35%. The difference between the residual values and a normal distribution is actually decreasing with the calculation time: the statistical uncertainty is not correctly estimated with a low number of events in the foils. Note that some points seem to be not perfectly normally distributed. Only 92% of the residuals are contained in 2 σ. If we focus on the residual at 10 keV for the foil number 6 (the orange point), the corresponding value is 4.1 σ, which is a large value even if possible with a low apparition frequency. If we focus on this point, and the previous one for comparison, the convergence of the flux value is plotted in Figure 7.
On the reference calculation of Figure 7 with an extra calculation time (not used for Fig. 6), we can see that the final red curve is much closer to the blue one: the residual reduces from 4.1 to 2.7 σ. An important element highlighted by this figure is that the reference flux value increases by successive gaps. These gaps correspond to specific batches where a neutron succeeds to reach the foil. There is no neutron in most of the batches. For this reason, the standard deviation is not correctly estimated because of the law of large number assumption in its estimation, even if the average value is correct.
Finally, concerning the FOM distribution (Fig. 6 bottom) we observe that, thanks to biasing, the variance is one order of magnitude smaller in the fast and epithermal regions. Moreover, the FOM reaches a factor of 50 in the thermal region of the spectrum for the foils located deep inside the metal reflector: the reference spectrum (top) is much more noisy for the yellow-orange curves at the energy of the thermal bump.
 |
Fig. 5 Weight map (top) for 0.1 to 1 meV (left) and 0.1 to 1 MeV (right) neutrons, together with the raw thermal (E < 0.3 eV) and fast (E > 0.1 eV) flux represented with a logarithmic scale (second line) and linear scale (third line), and finally the weighted flux in the core (last line). |
 |
Fig. 6 Neutron flux using a color gradient from blue to red when increasing the radial position of the dosimeter: without biasing as reference (top), with biasing (2nd line), residual (3rd line) and figure of merit (last line) with the average in black. |
 |
Fig. 7 Neutron flux estimation as a function of the calculation time, for the specific bin with a residual of 4.13 at 10 h (bottom) and another bin for comparison (top). The red curve is the reference calculation without biasing, and the blue curve is the result with the biasing. |
4 Uncertainty propagation and data assimilation principle
To optimise the quality of the experimental data that will be obtained with the PETALE experiment, a necessary but not sufficient condition is that the uncertainty propagation shows a larger impact from the nuclear data than the measurement uncertainty. In order to have this sufficient condition, the first step is the quantification of the propagation of nuclear data uncertainty.
4.1 Total Monte Carlo
The nuclear data uncertainty is expressed as a set of sampled cross sections with the TENDL2017 library (see Fig. 1). Each random cross section is associated to an ACE file. Each ACE file is used in a Monte Carlo calculation and provides a reaction rate value for each foil of the experiment. Finally, the image of the whole set of cross sections provides a distribution of reaction rates in the foils. The standard deviation of this distribution represents the nuclear data propagated uncertainty for the reaction rate. Note that for the Bayesian Monte Carlo (BMC) [6,17] assimilation step all the individual reaction rates for each ACE file are required.
The calculation cost of a Monte Carlo calculation for one set of iron ACE files (all isotopes of iron are considered) is around a day. Hundreds of sampled cross sections are required for uncertainty propagation. For this reason an acceleration technique based on correlated sampling has been developed and is detailed in the twin article [5]. The principle of the correlated sampling is the modelling of a macroscopic cross section modification by a modification of the neutron weight in order to be representative of the analogue and the modified systems in a single neutron track. This technique has been applied to the TENDL random cross sections, allowing to estimate 64 values of reaction rates instead of 1 with a single Monte Carlo calculation, the limitation being the memory (all the ACE file versions have to be loaded simultaneously).
 |
Fig. 8 Reaction rate dispersion in the foil detectors for the indium inelastic (top-left) and capture (top-right) reactions, the difference between each ACE file and the first ‘reference’ ACE file being represented in colours (bottom). |
4.2 Expected PETALE reaction rate dispersion
The eight metal plates are interleaved with nine activation foils in the experimental setup. In this way, the reaction rate evolution between the successive foils and by repeating the experiment with various foil compositions allows to measure theneutron spectra and amplitude evolution through the metal plates. Figure 8 presents the reaction rate as a function of the foil position for the indium capture (left) and inelastic (right) reactions, with the absolute value (top) and the relative dispersion between the random ACE files for a perturbation of all the iron isotopes.
This dispersion in the reaction rates is a useful piece of information on the target precision required to be able to constrain the nuclear data in the BMC process. We can see that the reaction rate dispersion of the prior nuclear data is around 20%. Thus a measurement precision around 1–2% can provide an important constraint, assuming that the nuisance parameters (dosimeter cross sections, experiment dimension, etc.) are low enough. Future developments will characterise the impact of these nuisance parameters on the reaction rates, such as the precision on the reflector position close to the core.
Note that in this preliminary study, thanks to the precision on the spectrum variation measurement through the heavy reflector, the shape of the reaction rate itself could be used for the data assimilation. The utilisation of the shape instead of the absolute measurement would provide a power normalisation free assimilation, and also substract biases coming from the efficiency uncertainty of the HPGe detection systems.
Indium (n,n’) and (n,γ) reaction rate dispersion in percents due to iron and aluminium for 32 ACE files.
4.3 Aluminium nuisance parameter
Even if the experiment is sensitive to the metal reflector in order to be able to constraint the related cross sections, other nuclear data uncertainties can also contribute to the total uncertainty on the reaction rates. In order to constrain the cross sections of the targeted isotopes, a limited impact of these nuisance parameters is mandatory. If the uncertainty propagation of another contributor is larger than the one induced by the metal reflector, the latter cross section improvement will be limited. Additionally, the quantification of this nuisance parameter uncertainty is mandatory to avoid compensation effects. Indeed, if there is an unquantified source of uncertainty, the assimilation of the experimental data would compensate the error due to this additional source of uncertainty on the metal reflector cross section themselves.
To illustrate this, in this section we consider the propagation of the aluminium cross section uncertainties on the reaction rates of the foils. In order to maximise this impact, the void space between the iron plates is replaced by an aluminium thin plate of 2 mm. This aluminium being one of the possible dosimeter positioners, we study here a realistic nuisance parameter of the experiment.
Figure 9 presents a comparison between the impact of the iron (dashed line) and of the aluminium (solid line) uncertainty using the first 32 ACE files. Additionally, Table 1 shows quantitative values of the reaction rate dispersion, the ‘maximal’ column being the maximal difference between two ACE files, the ‘σv max’ being the higher standard deviation obtained between the different volumes, and ‘σall v ’ being the standard deviation obtained using all the volumes together.
We can see that the propagation of the aluminium uncertainties has a much lower impact than the iron uncertainties. This mandatory condition to be able to constrain the iron cross section using the BMC technique is thus fulfilled. Moreover, from the standard deviation associated to the aluminium uncertainty on each foil detector, a systematic uncertainty will be reported in the error on the difference between the prediction and the measurement of the weight calculation of the ACE files in the BMC in order to avoid compensation effects.
 |
Fig. 9 Reaction rates in the foil detectors for the indium inelastic (top-left) and capture (top-right) reactions; the differences between each ACE file and the first ’reference’ ACE file of the iron and the aluminium are represented in colours (middle) respectively in dashed and solid lines. |
4.4 Inter-dosimeter correlation
The impact of the nuclear data uncertainty cannot be assumed to be independent between different dosimeters. For example, if we consider threshold reactions on indium and rhodium dosimeters, the reaction rate dispersions are presented in Figure 10.
Each ACE file is represented with the same color for both reactions in Figure 10. We can see that a very similar ordering of ACE files is obtained for the two dosimeters. For example the ACE file with the larger reaction rate value in the foils for both cases is the brown one; the yellow is the second one; then the blue and so on. This similar ordering means that the dosimeter responses to the nuclear data uncertainty are correlated.
Finally the correlation of the detector responses to the nuclear data uncertainty is represented for a given set of dosimeters in Figure 11. Each dosimeter material is represented by a sub-matrix on the diagonal. The different dosimeter positions of a given material correspond to the lines/columns of a sub-matrix. The cross correlation between the foil materials are represented by the sub-matrices off the diagonal. The ordering between the foils in the figure is based on the lethargy averaged incoming neutron energy at the reaction with the dosimeter.
We can see different sub-groups in Figure 11. Indium and rhodium inelastic reactions are very correlated as qualitatively observed with the ordering of the color curves in Figure 10. However we can see that they are not correlated with the thermal sensitive reactions. On the other hand, compared to the other threshold reactions with a higher averaged energy (vanadium, aluminium and so on), a partial correlation exists and this approach allows us to quantify this level of correlation. This means that for the BMC assimilation, some of the dosimeters will provide a redundant information (e.g. inelastic rhodium and indium)and some others will provide an independent information (e.g. indium and vanadium). Independent dosimeters allow to provide a good constraint on the metal reflector cross sections, while redondant dosimeters allow to cross-check the quality of the measurements.
 |
Fig. 10 Reaction rates in the foil detectors for the indium inelastic (right) and rhodium inelastic (left) reactions. |
 |
Fig. 11 Inter-dosimeter correlations associated to the propagation of the iron cross section uncertainties on the dosimeters reaction rates (top-right diagonal), with its standard deviation (bottom-left diagonal) estimated with a Jackknife resampling technique [18]. |
5 Conclusions and perspectives
The study and the optimisation of the PETALE integral experiment are performed using a TMC approach to quantify the possible gain on the nuclear data. This technique is applicable here thanks to specific developments. The variance reduction method is used to increase the number of simulated neutrons reaching the foil detector volumes, with a factor of merit larger than a hundred in the thermal region. Additionally, the correlated sampling technique allows us to replace multiple independent calculations for different ACE files in the TMC uncertainty propagation by a single calculation with reduced statistical uncertainty.
Thanks to these developments, different designs can be studied directly to compare the impact of the nuclear data uncertainty of the metalreflector and of other structural materials on the reaction rates in the detectors. An optimisation will be done to maximise the impact of the uncertainty of the metal reflector and limit all the other uncertainties, which represent nuisance parameters in the data assimilation. Future studies will also be carried out to include the impact of geometrical uncertainties on the design and on the positioning of the experimental setup close to the core. Finally, the utilisation of various foil materials together with different metal reflector compositions will also be investigated in order to study all the experimental setups that will be used.
Author contribution statement
Axel Laureau carried out the model development and numerical implementation, with the help of Vincent Lamirand for the PETALE related aspects and of Dimitri Rochman for the uncertainty propagation related aspects. Andreas Pautz supervised the project. All authors discussed the results and contributed to the final manuscript.
References
- V.P. Lamirand, M. Hursin, G. Perret, P. Frajtag, O. Pakari, A. Pautz, Future experimental programmes in the crocus reactor, in Conference proceedings of RRFM/IGORR 2016, no. EPFL-CONF-218310 (2016), pp. 284–292 [Google Scholar]
- V.P. Lamirand, G. Perret, S. Radman, D.J. Siefman, M. Hursin, P. Frajtag, A. Gruel, P. Leconte, P. Blaise, A. Pautz, Design of separated element reflector experiments in crocus: Petale, in ISRD16 International Symposium on Reactor Dosimetry, No. CONF, 2017 [Google Scholar]
- A. Santamarina, C. Vaglio, P. Blaise, J. Klein, N. Huot, O. Litaize, N. Thiollay, J. Vidal, The perle experiment for the qualification of PWR heavy reflectors, in Proc. of Int. Conf. on the Physics of Reactors: Nuclear Power: A Sustainable Resource (PHYSOR2008), 2008 [Google Scholar]
- C. Vaglio-Gaudard, A. Santamarina, P. Blaise, O. Litaize, A. Lyoussi, G. Noguère, J. Ruggieri, J. Vidal, Interpretation of PERLE experiment for the validation of iron nuclear data using Monte Carlo calculations, Nucl. Sci. Eng. 166, 89 (2010) [Google Scholar]
- A. Laureau, V. Lamirand, D. Rochman, A. Pautz, Uncertainty propagation based on correlated sampling technique for nuclear data applications, EPJ Nuclear Sci. Technol. 6, 8 (2020) [CrossRef] [EDP Sciences] [Google Scholar]
- A.J. Koning, D. Rochman, Modern nuclear data evaluation with the talys code system, Nucl. Data Sheets 113, 28412934 (2012) [CrossRef] [Google Scholar]
- J. Leppänen, M. Pusa, T. Viitanen, V. Valtavirta, T. Kaltiaisenaho, The Serpent Monte Carlo code: Status, development and applications in 2013, Ann. Nucl. Energy 82, 142 (2015) [Google Scholar]
- J. Paratte, R. Früh, U. Kasemeyer, M. Kalugin, W. Timm, R. Chawla, A benchmark on the calculation of kinetic parameters based on reactivity effect experiments in the crocus reactor, Ann. Nucl. Energy 33, 739 (2006) [CrossRef] [Google Scholar]
- U. Kasemeyer, R. Früh, J. Paratte, R. Chawla, Benchmark on kinetic parameters in the crocus reactor, in International Reactor Physics Experiments Handbook (IRPhE) (4440) (Ed. 2007) 94 (2007) [Google Scholar]
- T. Goorley, M. James, T. Booth, F. Brown, J. Bull, L. Cox, J. Durkee, J. Elson, M. Fensin, R. Forster et al., Initial mcnp6 release overview, Nucl. Technol. 180, 298 (2012) [Google Scholar]
- A. Laureau, Développement de modèles neutroniques pour le couplage thermohydraulique du MSFR et le calcul de paramètres cinétiques effectifs, Ph.D. thesis, Grenoble Alpes University, France, 2015 [Google Scholar]
- A. Laureau, L. Buiron, B. Fontaine, Local correlated sampling Monte Carlo calculations in the TFM neutronics approach for spatial and point kinetics applications, EPJ Nuclear Sci. Technol. 3, 16 (2017) [CrossRef] [EDP Sciences] [Google Scholar]
- A. Laureau, Y. Lederer, A. Krakovich, L. Buiron, B. Fontaine, Spatial analysis of unprotected transients in heterogeneous sodium fast reactors, Ann. Nucl. Energy 115, 554 (2018) [CrossRef] [Google Scholar]
- J. Leppänen, T. Viitanen, O. Hyvönen, Development of a Variance Reduction Scheme in the Serpent 2 Monte Carlo Code, in Proceedings of M&C, Jeju, Korea (2017), pp. 16–20 [Google Scholar]
- J. Hendricks, T. Booth, MCNP variance reduction overview, in Monte-Carlo Methods and Applications in Neutronics, Photonics and Statistical Physics (Springer, 1985), pp. 83–92 [CrossRef] [Google Scholar]
- Y.-K. Lee, Neutron deep penetration calculations in light water with Monte Carlo tripoli-4® variance reduction techniques, EPJ Web Conf. 153, 02011 (2017) [CrossRef] [Google Scholar]
- D. Rochman, E. Bauge, A. Vasiliev, H. Ferroukhi, Correlation ν¯p− σ− χ in the fast neutron range via integral information, EPJ Nuclear Sci. Technol. 3, 14 (2017) [CrossRef] [EDP Sciences] [Google Scholar]
- B. Efron, Nonparametric estimates of standard error: the jackknife, the bootstrap and other methods, Biometrika 68, 589 (1981) [CrossRef] [Google Scholar]
Cite this article as: Axel Laureau, Vincent Lamirand, Dimitri Rochman, Andreas Pautz, Uncertainty propagation for the design study of the PETALE experimental programme in the CROCUS reactor, EPJ Nuclear Sci. Technol. 6, 9 (2020)
All Tables
Indium (n,n’) and (n,γ) reaction rate dispersion in percents due to iron and aluminium for 32 ACE files.
All Figures
 |
Fig. 1 56 Fe cross-section selected randomly form ACE files of the TENDL2017 nuclear database (left) with a zoom on the first resonance (middle) and in the high energy (right) regions. The first ACE file (in red in the upper row) has been used as reference and the variation between this file and 32 versions of this cross section is displayed in the lower row. |
| In the text | |
 |
Fig. 2 Axial section of CROCUS represented using the Serpent2 code, with the addition of the PETALE metal reflector (top-left). The oxide uranium fuel is displayed in orange, the metal uranium fuel in red, and the water in blue. The four circles in the water reflector are fission and ionisation chambers used as CROCUS monitors. A zoom on the interface between CROCUS and the metal reflector shows the first foil with a width multiplied by 10 in order to be visible (1 g of indium for the first foil instead of 0.1 g). |
| In the text | |
 |
Fig. 3 Cross section of interest of different foil compositions. |
| In the text | |
 |
Fig. 4 Radial neutron flux in linear scale for different ranges: total (top-left), thermal (top-right), epithermal (bottom-left) and fast (bottom-right). The axial position used to score the flux corresponds to a 10 cm width gate centered around the PETALE device. |
| In the text | |
 |
Fig. 5 Weight map (top) for 0.1 to 1 meV (left) and 0.1 to 1 MeV (right) neutrons, together with the raw thermal (E < 0.3 eV) and fast (E > 0.1 eV) flux represented with a logarithmic scale (second line) and linear scale (third line), and finally the weighted flux in the core (last line). |
| In the text | |
 |
Fig. 6 Neutron flux using a color gradient from blue to red when increasing the radial position of the dosimeter: without biasing as reference (top), with biasing (2nd line), residual (3rd line) and figure of merit (last line) with the average in black. |
| In the text | |
 |
Fig. 7 Neutron flux estimation as a function of the calculation time, for the specific bin with a residual of 4.13 at 10 h (bottom) and another bin for comparison (top). The red curve is the reference calculation without biasing, and the blue curve is the result with the biasing. |
| In the text | |
 |
Fig. 8 Reaction rate dispersion in the foil detectors for the indium inelastic (top-left) and capture (top-right) reactions, the difference between each ACE file and the first ‘reference’ ACE file being represented in colours (bottom). |
| In the text | |
 |
Fig. 9 Reaction rates in the foil detectors for the indium inelastic (top-left) and capture (top-right) reactions; the differences between each ACE file and the first ’reference’ ACE file of the iron and the aluminium are represented in colours (middle) respectively in dashed and solid lines. |
| In the text | |
 |
Fig. 10 Reaction rates in the foil detectors for the indium inelastic (right) and rhodium inelastic (left) reactions. |
| In the text | |
 |
Fig. 11 Inter-dosimeter correlations associated to the propagation of the iron cross section uncertainties on the dosimeters reaction rates (top-right diagonal), with its standard deviation (bottom-left diagonal) estimated with a Jackknife resampling technique [18]. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


