| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
|
|
|---|---|---|
| Article Number | 15 | |
| Number of page(s) | 5 | |
| Section | Applied Covariances | |
| DOI | https://doi.org/10.1051/epjn/2018019 | |
| Published online | 29 June 2018 | |
https://doi.org/10.1051/epjn/2018019
Regular Article
Efficient use of Monte Carlo: the fast correlation coefficient
1
Department of Physics and Astronomy, Uppsala University,
Uppsala, Sweden
2
Nuclear Research and Consultancy Group NRG,
Petten, The Netherlands
3
Reactor Physics and Thermal Hydraulic Laboratory, Paul Scherrer Institut,
Villigen, Switzerland
* e-mail: henrik.sjostrand@physics.uu.se
Received:
16
January
2018
Received in final form:
16
February
2018
Accepted:
4
May
2018
Published online: 29 June 2018
Random sampling methods are used for nuclear data (ND) uncertainty propagation, often in combination with the use of Monte Carlo codes (e.g., MCNP). One example is the Total Monte Carlo (TMC) method. The standard way to visualize and interpret ND covariances is by the use of the Pearson correlation coefficient,
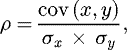
where x or y can be any parameter dependent on ND. The spread in the output, σ, has both an ND component, σND, and a statistical component, σstat. The contribution from σstat decreases the value of ρ, and hence it underestimates the impact of the correlation. One way to address this is to minimize σstat by using longer simulation run-times. Alternatively, as proposed here, a so-called fast correlation coefficient is used,
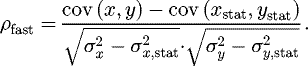
In many cases, cov(xstat; ystat) can be assumed to be zero. The paper explores three examples, a synthetic data study, correlations in the NRG High Flux Reactor spectrum, and the correlations between integral criticality experiments. It is concluded that the use of ρ underestimates the correlation. The impact of the use of ρfast is quantified, and the implication of the results is discussed.
© H. Sjöstrand et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Monte Carlo (MC) (or random sampling) methods are frequently used for nuclear data (ND) evaluation and uncertainty propagation. For ND uncertainty propagation, one frequently uses so-called random files, which is an MC representation of the full PDF of the ND, i.e., the random files implicitly contain both the best estimate of the ND and the associated uncertainty. The random files can be generated from the covariance matrix of the the ND library [1–3]. Alternatively, the Total Monte Carlo (TMC), method is used where the random files are generated directly from the underlying physics model parameter distributions [4]. For uncertainty propagation, an application code, e.g., MCNP, is run multiple times, each time with a new set of random files. The distribution of the output of these simulations can be interpreted in terms of the moments of the investigated output parameters, e.g., flux or keff. From the output from the large set of simulation with varying ND as input, the best estimate and the uncertainty can be inferred. I.e., the MC method commonly used in ND uncertainty propagation is a standard random sampling of input parameters. MC methods have the advantage that they propagate non-linear behavior. In addition, some methods, like the TMC method, can also propagate higher moments of input parameters, e.g., skewness and kurtosis. Unfortunately, MC methods are computationally expensive, especially when combined with MC codes, e.g., MCNP. This was partly addressed by the FAST-TMC method [5], where the uncertainty due to MC-code counting statistics and ND was separated.
Often, not only the uncertainty is sought but also the covariance between input and output parameters. Today's ND libraries contain covariances between different energies; cross-channel correlations are also available in modern evaluations [6,7]. In some cases, even cross-isotope correlations are available [8], however, this is something that has a large potential to be improved [9]. Correlations can also exist between ND and a specific application [10]. This can be used as a measure of the sensitivity of the application to a particular ND. In addition, correlations between integral experiments and a specific application can provide information on the applicability of the benchmark for the specific application [11]. Similarly, correlation between benchmarks is a measure of the benchmark's inter-similarity. Finally, correlations in outputs from an application can be needed to provide further uncertainty propagation or adjustment. A good example of the latter is the adjustment of the neutron spectrum using reactor dosimetry foils [12]. Today, the standard way to visualize and interpret ND covariances is by the use of the Pearson correlation coefficient, ρ. In this paper, we argue that this can be a biased estimate of the underlying ND correlation if the contribution from MC code counting statistics is not taken into account. This can lead to misinterpretations of the results. This paper explores three examples, a synthetic data study, correlations from the NRG High Flux Reactor spectrum [12] and correlations between different integral criticality experiments.
2 Method
As mentioned, ND covariances are often visualized by the use of the Pearson correlation coefficient,
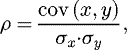 (1)
where x or y can be any parameter dependent on ND (e.g., the neutron flux at a specific energy or keff of a specific integral experiment). The cov(x, y) is the covariance between two parameters, e.g., the neutron flux at the energies E and E′. The cov(x, y) is determined as the sample covariance of the output from multiple simulations using the different random files as input. In this work, TENDL2014 and TENDL2015 random files [4,6] are used for the MCNP simulation. σ is the observed sample standard deviation from the output (for x and y), e.g., the observed spread in keff for a specific benchmark. As addressed in reference [5], σ has both an ND component, σND, and a statistical component σstat,
(1)
where x or y can be any parameter dependent on ND (e.g., the neutron flux at a specific energy or keff of a specific integral experiment). The cov(x, y) is the covariance between two parameters, e.g., the neutron flux at the energies E and E′. The cov(x, y) is determined as the sample covariance of the output from multiple simulations using the different random files as input. In this work, TENDL2014 and TENDL2015 random files [4,6] are used for the MCNP simulation. σ is the observed sample standard deviation from the output (for x and y), e.g., the observed spread in keff for a specific benchmark. As addressed in reference [5], σ has both an ND component, σND, and a statistical component σstat,
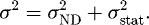 (2)
(2)
Similarly, the covariance contains both a statistical and an ND part,
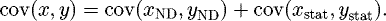 (3)
(3)
Combining equations (1)–(3) we obtain
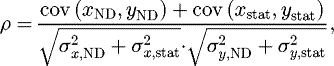 (4)
but what we really are interested in is the correlation due to ND,
(4)
but what we really are interested in is the correlation due to ND,
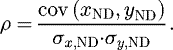 (5)
(5)
Using equation (1), and effectively equation (4), we see that the contribution from σstat decreases the value of ρ, and hence it is easy to underestimate the impact of the correlation from ND. One way to address this is to minimize σstat by using longer MC code run-times, e.g., more particles/histories in the case of MCNP. Alternatively, as proposed here, a so-called fast correlation coefficient is used,
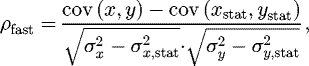 (6)
effectively subtracting the contribution from the MC codes statistics from the ρ in equation (1); equation (6) is effectively a combination of equations (2), (3) and (5). σstat is often estimated by the code, e.g., MCNP provides an estimate of the statistical uncertainty of the output parameters. In these cases, the average from all the simulations of the σstat is calculated and used in equation (6). This is also what has been done for the examples in this paper. In some cases, σstat is not estimated by the code, where one example is depletion calculations. In these cases, an additional set of simulations have to be performed to determine σstat; the ND is kept constant and only the random-seed is varied, and hence the spread of the observable is only due to statistics [5].
(6)
effectively subtracting the contribution from the MC codes statistics from the ρ in equation (1); equation (6) is effectively a combination of equations (2), (3) and (5). σstat is often estimated by the code, e.g., MCNP provides an estimate of the statistical uncertainty of the output parameters. In these cases, the average from all the simulations of the σstat is calculated and used in equation (6). This is also what has been done for the examples in this paper. In some cases, σstat is not estimated by the code, where one example is depletion calculations. In these cases, an additional set of simulations have to be performed to determine σstat; the ND is kept constant and only the random-seed is varied, and hence the spread of the observable is only due to statistics [5].
In addition, here, in this this paper, 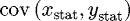 is assumed to be zero. The assumption is further discussed in Section 4.
is assumed to be zero. The assumption is further discussed in Section 4.
2.1 Test with synthetic data
The method was first tested with synthetic data with the assumption of an underlying ND covariance between 47 observables. The ND covariance, see Figure 1 left, was inspired by the data in reference [12], i.e., the 47 observables could represent the neutron flux in 47 energy bins. The average correlation between the observables was assumed to be 0.4. By sampling from the covariance matrix, 298 samples were generated. A statistical error was added to each observable in each sample. The magnitude of the statistical error was drawn for each sample from an assumed statistical error PDF (a Gaussian with an expected value of zero and a variance with twice the variance estimated in reference [12]). From the 298 samples, each with an added statistical component, new correlation matrices using both ρ (Fig. 1 middle) and ρfast (Fig. 1 right) were produced. As can be seen in Figure 1 middle, ρ underestimates the correlation as expected, whereas ρfast reproduces the mean underlying ND correlation.
The use of data from [12] as an inspiration for the synthetic data study is completely arbitrary; any correlation matrix and statistical variance could have been used to test the method.
 |
Fig. 1 Results for the synthetic data case. Left: the assumed ND correlation. Middle: the correlation obtained after adding statistics and using the usual Pearson correlation coefficient. Right: the correlation obtained after adding statistics and using the fast correlation coefficient. |
3 Test with real data
3.1 The NRG high flux reactor spectrum correlations
In reference [12], the TMC method was used to calculate the full covariance matrix of a neutron spectrum. For this MCNP and 300 TENDL2015 random files were used. The covariance matrix was subsequently used when adjusting the spectrum to dosimetry foils. In the paper, the correlation is represented using ρ. Unexpected low correlation coefficients were observed, from [12]: The correlation between the energy groups in the neutron spectra was weaker than we expected, especially if we compare it to the correlation matrix calculated by Williams et al. The paper correctly states: The covariance matrix calculated with the Total Monte Carlo method will only successfully show the covariances due to the nuclear data if the statistical uncertainty in each MCNP calculation is sufficiently small. It will be impossible to detect any weak coupling between two energy groups, if the statistical uncertainties are too high. In this paper, we test the ρfast on the same data to establish if the use of ρfast would obtain more expected correlations. We used the 47 grouped spectrum from the same data as in reference [12]. The results can be seen in Figure 2.
As can be seen, more expected correlations are obtained using ρfast. For five energy bins, the estimated σstat from the MCNP calculations are actually larger than the observed spread between the different samples. In these cases, no estimate of the correlation is obtained. This appears as white bands in the correlation plot in Figure 2 right. A general rule of thumb from [5] is that σstat < 0.5σ. For many of the spectral points in this data, this is not achieved. The ρfast obtains more expected correlations and the requirements on statistical convergence in the MCNP calculations can be relaxed when using the ρfast; even so, this particular data set would benefit, as also pointed out in reference [12], from performing the calculations with better statistics, in combination with using the ρfast.
 |
Fig. 2 Results for the NRG high flux reactor case. Left: the Pearson correlation coefficient obtained using the same data as in reference [12], but on a 47 group energy grid. Right: same as left, but using the fast correlation coefficient. |
3.2 Thermal criticality benchmarks
The impact of the method was also tested on a set of thermal criticality benchmarks, lct11, lct61, and lct71. These are low enriched U235, compound and thermal systems (with water) and their keff responses to the ND are expected to be highly correlated. From the ICSBEP DICE [13] tool the cross-sensitivity between the benchmarks are all quoted to be above 0.9. The benchmarks were all taken from the criticality handbook [14], and the simulations were performed using MCNP. In this case, TENDL2014 U235 [6] data were varied using 1000 random files. The σstat was around 250 pcm for the simulations. In Table 1 the results from ρfast are compared to the results for using ρ. As anticipated, higher, and more expected, correlations are obtained using the ρfast.
The method was also tested for mct011. Here the criteria σstat < 0.5σ was not met, and unrealistic results were obtained.
Correlation coefficients (keff responses to nuclear data) between lct11, lct61 and lct 71.
4 Discussion
Is the use of the ρfast coefficient important? What is actually used in error propagation or adjustment is the covariance matrix and not the correlation matrix, and in this sense, the bias in the correlation matrix is of less importance. However, the bias in the correlation matrix clearly affects our interpretation of the results as illustrated in reference [12]. Furthermore, in many cases, a lot of CPU time may be spent to obtain an unbiased ρ [10], which can be reduced dramatically if ρfast is used. In some cases, the correlation itself is used to judge the similarity between benchmarks and applications [11], and in these cases, a good judgment of the correlation is clearly important.
4.1 On cov(xstat, ystat)
An assumption of setting 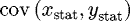 to zero is completely unproblematic in the case of different benchmarks since here the statistical processes of the simulations are completely independent. The authors believe that
to zero is completely unproblematic in the case of different benchmarks since here the statistical processes of the simulations are completely independent. The authors believe that 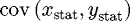 , should also be small in the case of [12] data, and hence the assumption to be reasonable. Ideally, this should be tested by repeating the simulations with constant ND and, e.g., 300 simulations with different seeds; hence the resulting covariances would only stem from the statistics. This has been outside the scope of this study. In some cases,
, should also be small in the case of [12] data, and hence the assumption to be reasonable. Ideally, this should be tested by repeating the simulations with constant ND and, e.g., 300 simulations with different seeds; hence the resulting covariances would only stem from the statistics. This has been outside the scope of this study. In some cases, 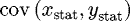 , can be assumed to be strong, e.g., for dependent reactor parameters. This has not been investigated in this study.
, can be assumed to be strong, e.g., for dependent reactor parameters. This has not been investigated in this study.
5 Conclusion
This paper presents a new correlation coefficient, ρfast, that should be considered when investigating correlations between MC code output parameters, obtained by random sampling. In these cases, the Pearson correlation coefficient, ρ, normally underestimates the correlation and ρfast addresses this issue. The paper presents theoretical arguments for the use of ρfast by its derivation. In addition, a synthetic data study supports the use of the method. The paper also presents two real cases where the method is used. In these cases, it is harder to draw unambiguous conclusions since the true correlation is unknown. However, the two studies indicate that the usual ρ underestimates the correlation. The presented method is a natural continuation of the fast TMC method presented in reference [5].
The method is tested for ND error propagation when using the neutron transport code MCNP. However, it should be relevant for any type of input parameter variation in any type of MC code.
Authors contributions
All the authors have contributed to the scientific content of the paper and approved the final manuscript.
References
- O. Buss, A. Hoefer, J.C. Neuber, in Nuduna: Towards a Complete Nuclear Data Uncertainty Estimation for Criticality Safety Applications International, Conference on Nuclear Criticality 2011, Edinburgh (2011) [Google Scholar]
- T. Zhu, A. Vasiliev, H. Ferroukhi, A. Pautz, Ann. Nucl. Energy 75, 713 (2015) [CrossRef] [Google Scholar]
- L. Fiorito et al., Ann. Nucl. Energy 101, 359 (2017) [CrossRef] [Google Scholar]
- A.J. Koning, D. Rochman, Nucl. Data Sheets 113, 2841 (2012) [CrossRef] [Google Scholar]
- D. Rochman, Nucl. Sci. Eng. 177, 337 (2014) [CrossRef] [Google Scholar]
- A.J. Koning, D. Rochman et al., TALYS-Based Evaluated Nuclear Data Library, https://tendl.web.psi.ch/tendl_2015/tendl2015.html. [Google Scholar]
- P. Helgesson, H. Sjöstrand, D. Rochman, Nucl. Data Sheets 145, 1 (2017) [CrossRef] [Google Scholar]
- O. Iwamoto, T. Nakagawa, S. Chiba, J. Kor. Phys. Soc. 59, 1224 (2011) [Google Scholar]
- D. Rochman et al., EPJ Nuclear Sci. Technol. 4, 7 (2018) [Google Scholar]
- E. Alhassan et al., Ann. Nucl. Energy 75, 26 (2015) [CrossRef] [Google Scholar]
- E. Alhassan et al., Ann. Nucl. Energy 96, 26 (2016) [CrossRef] [Google Scholar]
- N.L. Asquith, S.C. van der Marck, in 16th International Symposium of Reactor Dosimetry (ISRD16) (2017) [Google Scholar]
- https://www.oecd-nea.org/science/wpncs/icsbep/dice.html [Google Scholar]
- https://www.oecd-nea.org/science/wpncs/icsbep/handbook.html [Google Scholar]
Cite this article as: Henrik Sjöstrand, Nicola Asquith, Petter Helgesson, Dimitri Rochman, Steven van der Marck, Efficient use of Monte Carlo: the fast correlation coefficient, EPJ Nuclear Sci. Technol. 4, 15 (2018)
All Tables
Correlation coefficients (keff responses to nuclear data) between lct11, lct61 and lct 71.
All Figures
 |
Fig. 1 Results for the synthetic data case. Left: the assumed ND correlation. Middle: the correlation obtained after adding statistics and using the usual Pearson correlation coefficient. Right: the correlation obtained after adding statistics and using the fast correlation coefficient. |
| In the text | |
 |
Fig. 2 Results for the NRG high flux reactor case. Left: the Pearson correlation coefficient obtained using the same data as in reference [12], but on a 47 group energy grid. Right: same as left, but using the fast correlation coefficient. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


