EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 4 (2018) EPJ Nuclear Sci. Technol., 4 (2018) 16 Full HTML
Issue
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
Article Number 16
Number of page(s) 8
Section Nuclear Models
DOI https://doi.org/10.1051/epjn/2018014
Published online 29 June 2018

© S. Hilaire et al., published by EDP Sciences, 2018

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

The modeling of nuclear reactions involves several models connected with each other to produce nuclear data. Three main models (Fig. 1) are usually employed in modern nuclear reaction codes such as TALYS [1] or EMPIRE [2]: the optical model, the pre-equilibrium model and the compound nucleus model. All these models rely on a large number of inputs as well as on more or less valid approximations. Even though it is possible nowadays to reproduce, with a rather good accuracy, available experimental data by adjusting the various parameters driving the nuclear reaction models, several approximations are still known to be compensated by these parameter adjustment and/or by an interplay between the models themselves. It is therefore important, to improve our understanding of the physical processes occuring during a nuclear reaction as well as the predictive power of the modeling itself, to be able to reduce the sources of error compensation by suppressing some of the approximations known to play a role or by improving the modeling of specific inputs required by nuclear models. In this paper, we illustrate some important issues which we think should be carefully accounted for to reduce potential sources of uncertainties in the evaluation process. Section 2 discusses the optical model which has to be as accurate as possible. Indeed, since this model is at the basis of the evaluation process, any error or inaccuracy it yields has an impact on both the pre-equilibrium and the compound nucleus model which must then be tuned to compensate the possible deficiencies of the optical model. Section 3 focuses on the differences that can be obtained depending upon whether one uses a classical pre-equilibrium model or a more microscopic approach to populate the compound nucleus before it decays. Section 4 illustrates few other sources of uncertainties such as those related to the fission channel, the width fluctuation correction factor (WFCF) or the gamma-ray strength functions, required as inputs to the compound nucleus model. Conclusions and prospects are finally drawn in Section 5.

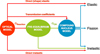thumbnail Fig. 1

Flowchart of the sequence of models required to describe a nuclear reaction. The optical model enables to separate the incident flux (total cross-section) in three separate contributions (the shape elastic, the reaction and the direct inelastic cross-sections) and provides the compound nucleus with light particles transmission coefficients. Part of the reaction cross-section (σReaction) is then processed with the pre-equilibrium model to feed inelastic channels as well as the compound nucleus model with the remaining flux (σCN). σCN is then spread over all outgoing channels by the compound nucleus model.

2 The optical model

As illustrated in Figure 1, the optical model is the first model used in the nuclear reaction modeling. This model enables to separate the incident projectile flux into three main components: the shape elastic, the direct inelastic and the reaction cross-sections. It also provides transmission coefficients for light particles whose emission is treated within the compound nucleus model framework. As a consequence, any error or inaccuracy introduced at this level of the modeling process will directly influence the following steps, namely the pre-equilibrium and the compound nucleus models. Several approaches are available to construct an optical model potential. Microscopic methods aiming at producing an Optical Model Potential (OMP) [3–6] based on nucleon–nucleon interactions are not yet usable for evaluation purposes due to their lack of accuracy or to a too narrow range of application. Therefore phenomenological [7–9] or semi-microscopic approaches [10–12] are usually employed for applications.

When many experimental data are available, phenomenological approaches are clearly prefered since the number of parameters on which they rely provide with a high degree of flexibility and the possibility to obtain very accurate fits of measured data. However, the price to pay is then an in depth analysis of the sensitivity of the output to the input parameters. In the case of a deformed target, beyond the OMP parameters, the adopted coupling scheme as well as the deformation parameters also play a crucial role. A typical illustration of the impact of the number of inelastic levels introduced in coupled channel (CC) methods is shown in Figure 2. As can be observed, the total cross-sections reaches rather similar values, at least compatible with experimental data within error bars, for various choices of the number of coupled levels while the compound nucleus formation cross-section remains much more sensitive to the choice of the coupling scheme. With such differences, the other channels predictions, in particular the fission cross-section, will be clearly influenced by the number of coupled levels considered, meaning that uncertainties in the fission channel do not only depend on the sole uncertainties on fission model parameters, as it might be thought at first glance.

In the case of the so-called Jeukenne-Lejeune-Mahaux (JLM) semi-microscopic [10–12] approach, one does not have the freedom to fit cross-section as for the phenomenological OMP. Indeed, the free parameters of the approach have been fixed on a selected set of nuclei and are not modified when changing the target. The only freedom is then linked to the structure description of the target. For a 28 MeV (p,p′) reaction on 36S for instance (Fig. 3), it can be observed that describing the target nucleus within the quasiparticle random phase approximation (QRPA) framework [13,14] enables to reproduce available experimental data for inelastic scattering off the 2+ level better than when the five-dimensional collective hamiltonian (noted GCM for Generator Coordinate Method in Fig. 3) approach [15] is used, while the elastic scattering is almost not modified.

thumbnail Fig. 2

Total (σtot) and compound nucleus formation (σCN) cross-sections obtained increasing the number of coupled levels in the coupled channel approach for neutron induced reaction on 235U.
thumbnail Fig. 3

(p,p′) angular distribution on 36S for the ground state and first 2+ state using two microscopic structure approaches (GCM or QRPA see text for details) to determine transition densities required for a coupled channel calculation within the semi-microscopic JLM approach.

3 The pre-equilibrium model

Another feature which is known to impact the cross-section determination for various reactions is related to the modeling of the pre-equilibrium emission mechanism for which one or several particles are emitted before a compound nucleus is formed. In many applications, pre-equilibrium is described within the phenomenological exciton model which is semi-classical and contains parameters tuned on a relevant set of (n,xn) and (p,xp) observables. An alternative method, recently developed [16,17], employs the QRPA nuclear structure model [13,14] in a relevant microscopic reaction approach, the JLM folding model, to determine the fast excitation mechanism of the target nuclei which occurs during the pre-equilibrium process. Depending upon the method employed, the compound nucleus population after such direct-like interaction, is strongly modified. This is illustrated in Figure 4 for a 238U(n,n′γ) reaction. After the pre-equilibrium emission of a neutron, the formed compound nucleus has a spin population which peaks at much lower values when a microscopic approach is used and the spin distribution structure does not follow the statistical Wigner distribution associated to the exciton model.

This aspect strongly impacts the determination of gamma-ray emission cross-sections for transitions between discrete states of the residual nucleus. Indeed, if the compound nucleus is formed with mainly low spin, the system will have to go through many transitions to reach a high spin. Thus γ-emission from states with high spin will be strongly hindered. Figure 5 illustrates this aspect as it shows that calculations based on the exciton model and the Wigner spin distribution over-predict (n,n′γ) transition from the 10+ state while the QRPA-based approach provides a magnitude in agreement with the measured values.

It would be possible to mimic the QRPA-based spin distribution adjusting the Wigner spin distribution parameters but such an effectiveness would clearly hide a misunderstanding of the physics in order to fit the observed transition.

thumbnail Fig. 4

Compound nucleus spin distribution of the 238U compound nucleus formed after a fast neutron emission. The Wigner distribution associated to the exciton model is compared to the QRPA-based approach of references [16,17].
thumbnail Fig. 5

238U(n,n′γ) cross-sections for two transitions in the ground state rotational band (see details on plots). Two Talys calculations, which used the exciton (dashed black curves) or the JLM/QRPA model (full red curves) for pre-equilibrium, are compared to experimental data (symbols) [18–20].

4 The compound nucleus model

The compound nucleus model is the last model involved in the evaluation of nuclear reaction. This model, based on the statistical Hauser-Feshbach approach, provides the cross-section between an incident channel a and an outgoing channel b as 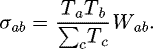(1) In equation (1), Ta and Tb correspond to the incident and outgoing transmission coefficients, the sum ∑cTc runs over all open channels and Wab is the WFCF accounting for the fact that the entrance and outgoing channel are not totally independent [21]. It has been recently demonstrated [22–24] that, for well deformed nuclei, the usually neglected Engelbrecht-Weidenmüller transformation (EWT) [25], known to be required for a rigourous description of the WFCF was playing a rather important role. More precisely, whereas it was thought that the WFCF only enhances the elastic channel and decreases all inelastic channel, it has been shown that for inelastic levels strongly coupled to the ground state, an enhancement of the inelastic cross-section was also observed. This effect is illustrated in Figure 6 where a comparison is shown between various predictions and the direct inelastic cross-section off the first 2+ level in 238U.

One can understand that if the EWT is accounted for, the adjustment of the OMP parameters enabling to fit available experimental data will not be the same as if one does not account for the EWT, unless the energy region where the EWT plays a role is not used to constrain the OMP parameters. It is thus clear that if the EWT effects are hidden in the parameters entering the definition of the OMP, avoidable error compensations are introduced in the evaluation.

Another example of compensation effect is also illustrated in Figure 7. In this case, one can study the impact of the coupling scheme considered in the CC-OMP when looking at the corresponding fission cross-sections. Depending on the number of coupled levels introduced, the fission cross-section varies significantly, reflecting, as shown in Figure 2, the way the number of coupled level modifies the compound nucleus formation cross-section. One could of course improve, for each choice of the coupling scheme, the fit of the fission cross-section by fine tuning the fission model parameters. This would however mean that the fission model would counterbalance a restricted coupling scheme in the CC approach.

The gamma emission is also a nice illustration of compensation effects. Within the Brink-Axel hypothesis [27,28], the gamma transmission coefficient reads 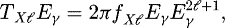(2) where Eγ is the energy of the emitted gamma of type X (X = E or M for electric or magnetic transitions) and multipolarity ℓ, and where fXℓ(Eγ) is the energy dependent gamma-ray strength function whose analytical expression follows a Lorentzian shape. For thermal neutrons, the compound nucleus excitation energy corresponds to the neutron separation energy Sn and the average radiative with Γγ is entirely due to s-wave neutrons, so that the gamma-ray strength function satisfies the following equation 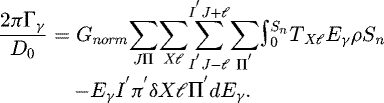(3)In this equation, the J, Π sum runs over the compound nucleus states with spin J and parity Π that can be formed with s-wave incident neutrons and I′, Π′ denote the spin and parity of the final states to which a photon of type X with multipolarity ℓ can be emitted. The multipole selection rules are δ(X = E, ℓ , Π′) = 1 if Π = (− 1)ℓΠ′ for Electric transition, δ(X = M, ℓ , Π′) = 1 if Π = (− 1)ℓ+1Π′ for magnetic transitions and δ(X, ℓ , Π′) = 0 otherwise. Finally, ρ is the compound nucleus nuclear level density and D0 the average spacing of s-wave resonances. In practice, whereas Gnorm should be equal to unity, one often has to use a different value for Gnorm to ensure equation (3) is verified. Hence, the gamma transmission coefficient is multiplied by an arbitrary normalization factor Gnorm, which is compensating for the level density option that can be chosen when modeling a nuclear reaction and/or for deficiencies of the chosen gamma strength function. An illustration of this compensation is given in Figure 8.

In this figure, the 56Fe neutron capture is shown using various level density models for the 57Fe compound nucleus keeping the same gamma-ray strength function expressions (Kopecky and Uhl [33] for E1 and Standard Lorentzian [27,28] otherwise). Thanks to the normalization of equation (3), one can observe that very similar cross-section predictions are obtained. However, the corresponding gamma-ray strength functions are strongly modified by the normalizations depending on the level density option. It is therefore clear that if the normalization procedure of equation (3) enables to reproduce capture cross-sections data, photoabsorption cross-section will not be always reproduced.

A more refined approach has been recently studied to solve such an inconsitency. It consists in introducing an arbitrary low energy extra gamma-ray strength constrained to simultaneously describe capture and photoabsorption data [37–39]. The justification for such an extra strength stems from the fact that several experiment have reported, for low gamma-ray energies, strengths which are higher than the usually adopted analytical expression that have been adjusted to reproduce experimental data at energies above the region where such disagreement are observed. In this case, one can obtain Gnorm values which are closer to unity by enhancing locally the gamma-ray strength without modifying the high energy agreement with photoabsorption data. This procedure is illustrated in Figure 9 for the 177Lu E1 and M1 strengths.

By adding a supplementary M1 component, as shown in Figure 10, one manages to fit without any normalization the available data for the capture cross-section, and since this extra component is located far from the giant resonance peak, it has no impact on the description of the 10–15 MeV region where E1 strength dominates. It is worth noticing that without such an extra-M1 strength, a normalization factor Gnorm = 3.6 must be used to fit the experimental capture cross-section data, which also affect the 10–15 MeV region by the same magnitude. The M1 extra-strength is not yet confirmed experimentally but large scale QRPA calculations tend to confirm such a feature [40,41]. Indeed, using such a microscopic alternative for both nuclear level densities and gamma-ray strength function, one can observe, as shown in Figure 11 that a very satisfactory description of the experimental data can also be obtained.

Last but not least, the fission cross-section modeling is also at the source of many possible uncertainties. Indeed, if one manages to perform very accurate fits of available experimental data using phenomenological approaches [8], it is at the price of a fine tuning of a large number of adjustable parameters whose extrapolation might be very hazardous. Attempts to reduce this number of parameters using microscopic predictions [42] have shown that a rather reasonable agreement with data could be achieved, even, as illustrated in Figure 12, within a coherent approach consisting in constraining the adjustable parameters by a simultaneous fit of all relevant data [43]. Such microscopic approaches can clearly not compete with phenomenological approaches to accurately describe well measured actinides, but they offer an interesting alternative for unmeasured nuclei due to the reduced number of parameters on which they rely and the possibility one has to extrapolate them.

thumbnail Fig. 6

Inelastic cross-section off the first 2+ level of 238U as function of the excitation energy En. The red (resp. black) line shows the theoretical prediction obtained using (resp ignoring) the EWT with the Soukhovitski optical model potential [26]. The blue line shows the predictions obtained ignoring width fluctuation corrections. Experimental data are taken from the EXFOR database [29].
thumbnail Fig. 7

Fission cross-section obtained increasing the number of coupled levels in the CC approach for neutron induced reaction on 235U.
thumbnail Fig. 8

Top panel: 56Fe(n,γ)57Fe cross-section as function of the neutron incident energy. The black squares correspond to EXFOR data [29], the full black line is the prediction obtained using the default level density model implemented in the TALYS code [1,30], the red dotted line using the combinatorial level density model of Ref. [31] and the green dashed line the combinatorial level density model of Ref. [32]. Bottom panel: ratio between the strength functions obtained after the normalization deduced from equation (3) is applied and the strength function corresponding to the default level density option.
thumbnail Fig. 9

E1 and M1 strength function of 177Lu. The full black line shows the so-called Kopecky and Uhl [33] model implemented in TALYS for the E1 strength. The dashed red line corresponds to the default model for the M1 strength, namely the standard Lorentzian model [27,28]. The full red line shows the M1 strength obtained introducing a supplementary component in the M1 strength with a second Lorentzian centered around 4 MeV.
thumbnail Fig. 10

176Lu(n,γ)177Lu cross-section as function of the incident neutron energy E. The dotted blue line show the predictions obtained using the default options of the TALYS code for the level density and gamma-ray strength function as well as a normalization Gnorm = 3.6. The full black line shows the predictions obtained adding on top of the defaut prescriptions a low energy M1 strength without any normalization (Gnorm = 1). Experimental data are taken from references [34–36].
thumbnail Fig. 11

176Lu(n,γ)177Lu cross-section as function of the incident neutron energy E. The full red line show the predictions obtained using microscopic inputs for both the NLD and GSF. The full black line shows the predictions obtained adding on top of the defaut prescriptions a low energy M1 strength. In both cases Gnorm = 1.
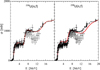thumbnail Fig. 12

Neutron induced fission cross-section on 238U using only fission cross-section as constraint (left panel) or including other relevant channels (right panel) as constraints. The reduced number of parameters gives less freedom to the fine tuning and therefore provides with a worse fit within the coherent approach (see Refs. [42,43] for more details).

5 Conclusions

The models currently used for evaluation of nuclear data require fine tuning of their parameters in order to maximize the agreement between calculated observables and experimental ones. Sometimes, obtaining a satisfactory agreement with experimental data is not even possible. In this case, for the short term, the amplitude of the disagreement must be included in the evaluation of uncertainties, whereas, for the longer term, better models can be built. Sometimes, achieving a good calculation-experiment agreement is done at the price of large adjustments of the model parameters, maybe even towards values that are not physical. Those model parameters thus transport both physical information and effective information which allows an approximate model to account for experimental data. Finally, there are sometimes ambiguities with different sets of model parameters producing equally good account of experimental data: error compensations. All the above cases are evidences of the need for better, less approximate nuclear models and more microscopic, less effective model parameters.

The examples, shown in the present paper, highlight the progresses made possible by adopting more exact, less approximate models, in the continuum energy range, for all three classes of processes : direct reactions, pre-equilibrium and statistical model. Moreover, those examples illustrate the possibility to compute the values of model parameters from a microscopic theory (using the nuclear interaction and many-body formalism with nucleonic degrees of freedom). Although the values of these “microscopic” model parameters still need to be adjusted to meet the needs of evaluated data files, the dynamics of these adjustments are strongly reduced, leaving less room for ambiguities and compensations.

However, the spectacular progress achieved for non-fissioning system, must not occult challenges ahead for the microscopic modeling of the fission channel with the needed precision. The high sensitivity of fission models to parameters like barrier heights, makes it unlikely to ever succeed in predicting fission cross-sections without sizable parameter adjustments. Nevertheless, similarly to non-fission channels, microscopic calculations should help reduce the fission model parameters adjustment dynamics.

For the foreseeable future, nuclear models will never be perfect, and therefore there will always be a need to quantify model defects into nuclear data covariances. However, since the use of microscopic nuclear models can often be shown to reduce the amplitude of model parameters adjustments, and simultaneously improve the quality of the agreement between calculation and experiment, using these better models is an opportunity to reduce the amplitude of those model defects at the source.

Author contribution statement

All the authors were involved in the preparation of the manuscript. All the authors have read and approved the final manuscript.

References

  1. A.J. Koning, S. Hilaire, M.C. Duijvestijn, in Proceedings of the International Conference on Nuclear Data for Science and Technology, April 22–27, 2007, Nice, France, edited by O. Bersillon, F. Gunsing, E. Bauge, R. Jacqmin, S. Leray (EDP Sciences, 2008), pp. 211–214 [Google Scholar]
  2. M. Herman et al., Nucl. Data Sheets 108, 2655 (2007) [Google Scholar]
  3. G. Blanchon et al., Phys. Rev. C 91, 014612 (2015) [CrossRef] [Google Scholar]
  4. J. Rotureau et al., Phys. Rev. C 95, 024315 (2017) [CrossRef] [Google Scholar]
  5. M. Dupuis et al., Phys. Rev. C 73, 014605 (2006) [CrossRef] [Google Scholar]
  6. K. Mizuyama, K. Ogata, Phys. Rev. C 86, 041603 (2012) [CrossRef] [Google Scholar]
  7. A.J. Koning, J.P. Delaroche, Nucl. Phys. A 713, 231 (2003) [NASA ADS] [CrossRef] [Google Scholar]
  8. P. Romain, B. Morillon, H. Duarte, Nucl. Data Sheets 131, 222 (2016) [CrossRef] [EDP Sciences] [Google Scholar]
  9. E.S. Soukhovitski et al., Phys. Rev. C 94, 064605 (2016), and references therein [CrossRef] [Google Scholar]
  10. J.-P. Jeukenne, A. Lejeune, C. Mahaux, Phys. Rev. C 16, 80 (1977) [NASA ADS] [CrossRef] [Google Scholar]
  11. E. Bauge, J.P. Delaroche, M. Girod, Phys. Rev. C 58, 1118 (1998) [CrossRef] [Google Scholar]
  12. E. Bauge, J.P. Delaroche, M. Girod, Phys. Rev. C 63, 024607 (2001) [CrossRef] [Google Scholar]
  13. J.P. Blaizot, D. Gogny, Nucl. Phys. A 284, 429 (1977) [CrossRef] [Google Scholar]
  14. S. Péru et al., Phys. Rev. C 83, 014314 (2011) [CrossRef] [Google Scholar]
  15. J. Libert, M. Girod, J.P. Delaroche, Phys. Rev. C 60, 054301 (1999) [CrossRef] [Google Scholar]
  16. M. Dupuis et al., Eur. Phys. J. A 51, 168 (2015) [CrossRef] [EDP Sciences] [Google Scholar]
  17. M. Dupuis et al., EPJ Web Conf. 146, 12002 (2017) [Google Scholar]
  18. M. Kerveno et al., Eur. Phys. J. A 51, 167 (2015) [CrossRef] [EDP Sciences] [Google Scholar]
  19. A. Hutcheson et al., Phys. Rev. C 80, 014603 (2009) [CrossRef] [Google Scholar]
  20. N. Fotiades et al., Phys. Rev. C 69, 024601 (2004) [CrossRef] [Google Scholar]
  21. S. Hilaire, A.J. Koning, C. Lagrange, Ann. Phys. 306, 209 (2003) [NASA ADS] [CrossRef] [Google Scholar]
  22. R. Capote et al., Nucl. Data Sheets 118, 26 (2014) [CrossRef] [Google Scholar]
  23. T. Kawano, P. Talou, H.A. Weidenmüller, Phys. Rev. C 92, 044617 (2015) [CrossRef] [Google Scholar]
  24. T. Kawano et al., Phys. Rev. C 94, 014612 (2016) [CrossRef] [Google Scholar]
  25. C.A. Engelbrecht, H.A. Weidenmüller, Phys. Rev. C 8, 859 (1973) [CrossRef] [Google Scholar]
  26. E.S. Soukhovitski et al., J. Phys. G: Nucl. Part. Phys 30, 905 (2004) [CrossRef] [Google Scholar]
  27. D.M. Brink, Nucl. Phys. 4, 215 (1957) [CrossRef] [Google Scholar]
  28. P. Axel, Phys. Rev. 126, 671 (1962) [Google Scholar]
  29. International Network of Nuclear Reaction Data Centres (NRDC), EXFOR database. Available at http://www-nds.iaea.org/exfor/exfor.htm [Google Scholar]
  30. A.J. Koning, S. Hilaire, S. Goriely, Nucl. Phys. A 810, 13 (2008) [Google Scholar]
  31. S. Goriely, S. Hilaire, A.J. Koning, Phys. Rev. C 78, 064307 (2008) [Google Scholar]
  32. S. Hilaire et al., Phys. Rev. C 86, 064317 (2012) [CrossRef] [Google Scholar]
  33. J. Kopecky, M. Uhl, Phys. Rev. C 41, 1941 (1990) [CrossRef] [Google Scholar]
  34. K. Wisshak et al., Phys. Rev. C 73, 015807 (2006) [NASA ADS] [CrossRef] [Google Scholar]
  35. O. Roig et al., Phys. Rev. C 93, 034602 (2016) [CrossRef] [Google Scholar]
  36. H. Beer, et al., Phys. Rev. C 30, 464 (1984) [CrossRef] [Google Scholar]
  37. J.L. Ullmann et al., Phys. Rev. C 89, 034603 (2014) [CrossRef] [Google Scholar]
  38. D. Denis-Petit et al., Phys. Rev. C 94, 054612 (2016) [CrossRef] [Google Scholar]
  39. M.R. Mumpower et al., Phys. Rev. C 94, 024612 (2017) [CrossRef] [Google Scholar]
  40. M. Martini et al., Phys. Rev. C 94, 014304 (2016) [CrossRef] [Google Scholar]
  41. S. Goriely et al., Phys. Rev. C 94, 044306 (2016) [CrossRef] [Google Scholar]
  42. S. Goriely et al., Phys. Rev. C 79, 024612 (2009) [NASA ADS] [CrossRef] [Google Scholar]
  43. S. Goriely et al., Phys. Rev. C 83, 034601 (2011) [CrossRef] [Google Scholar]

Cite this article as: Stephane Hilaire, Eric Bauge, Pierre Chau Huu-Tai, Marc Dupuis, Sophie Péru, Olivier Roig, Pascal Romain, Stephane Goriely, Potential sources of uncertainties in nuclear reaction modeling, EPJ Nuclear Sci. Technol. 4, 16 (2018)

All Figures

thumbnail Fig. 1

Flowchart of the sequence of models required to describe a nuclear reaction. The optical model enables to separate the incident flux (total cross-section) in three separate contributions (the shape elastic, the reaction and the direct inelastic cross-sections) and provides the compound nucleus with light particles transmission coefficients. Part of the reaction cross-section (σReaction) is then processed with the pre-equilibrium model to feed inelastic channels as well as the compound nucleus model with the remaining flux (σCN). σCN is then spread over all outgoing channels by the compound nucleus model.
In the text
thumbnail Fig. 2

Total (σtot) and compound nucleus formation (σCN) cross-sections obtained increasing the number of coupled levels in the coupled channel approach for neutron induced reaction on 235U.
In the text
thumbnail Fig. 3

(p,p′) angular distribution on 36S for the ground state and first 2+ state using two microscopic structure approaches (GCM or QRPA see text for details) to determine transition densities required for a coupled channel calculation within the semi-microscopic JLM approach.
In the text
thumbnail Fig. 4

Compound nucleus spin distribution of the 238U compound nucleus formed after a fast neutron emission. The Wigner distribution associated to the exciton model is compared to the QRPA-based approach of references [16,17].
In the text
thumbnail Fig. 5

238U(n,n′γ) cross-sections for two transitions in the ground state rotational band (see details on plots). Two Talys calculations, which used the exciton (dashed black curves) or the JLM/QRPA model (full red curves) for pre-equilibrium, are compared to experimental data (symbols) [18–20].
In the text
thumbnail Fig. 6

Inelastic cross-section off the first 2+ level of 238U as function of the excitation energy En. The red (resp. black) line shows the theoretical prediction obtained using (resp ignoring) the EWT with the Soukhovitski optical model potential [26]. The blue line shows the predictions obtained ignoring width fluctuation corrections. Experimental data are taken from the EXFOR database [29].
In the text
thumbnail Fig. 7

Fission cross-section obtained increasing the number of coupled levels in the CC approach for neutron induced reaction on 235U.
In the text
thumbnail Fig. 8

Top panel: 56Fe(n,γ)57Fe cross-section as function of the neutron incident energy. The black squares correspond to EXFOR data [29], the full black line is the prediction obtained using the default level density model implemented in the TALYS code [1,30], the red dotted line using the combinatorial level density model of Ref. [31] and the green dashed line the combinatorial level density model of Ref. [32]. Bottom panel: ratio between the strength functions obtained after the normalization deduced from equation (3) is applied and the strength function corresponding to the default level density option.
In the text
thumbnail Fig. 9

E1 and M1 strength function of 177Lu. The full black line shows the so-called Kopecky and Uhl [33] model implemented in TALYS for the E1 strength. The dashed red line corresponds to the default model for the M1 strength, namely the standard Lorentzian model [27,28]. The full red line shows the M1 strength obtained introducing a supplementary component in the M1 strength with a second Lorentzian centered around 4 MeV.
In the text
thumbnail Fig. 10

176Lu(n,γ)177Lu cross-section as function of the incident neutron energy E. The dotted blue line show the predictions obtained using the default options of the TALYS code for the level density and gamma-ray strength function as well as a normalization Gnorm = 3.6. The full black line shows the predictions obtained adding on top of the defaut prescriptions a low energy M1 strength without any normalization (Gnorm = 1). Experimental data are taken from references [34–36].
In the text
thumbnail Fig. 11

176Lu(n,γ)177Lu cross-section as function of the incident neutron energy E. The full red line show the predictions obtained using microscopic inputs for both the NLD and GSF. The full black line shows the predictions obtained adding on top of the defaut prescriptions a low energy M1 strength. In both cases Gnorm = 1.
In the text
thumbnail Fig. 12

Neutron induced fission cross-section on 238U using only fission cross-section as constraint (left panel) or including other relevant channels (right panel) as constraints. The reduced number of parameters gives less freedom to the fine tuning and therefore provides with a worse fit within the coherent approach (see Refs. [42,43] for more details).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.