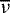| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
|
|
|---|---|---|
| Article Number | 7 | |
| Number of page(s) | 10 | |
| DOI | https://doi.org/10.1051/epjn/2018006 | |
| Published online | 15 May 2018 | |
https://doi.org/10.1051/epjn/2018006
Regular Article
Nuclear data correlation between different isotopes via integral information
1
Laboratory for Reactor Physics Systems Behaviour, Paul Scherrer Institut,
Villigen, Switzerland
2
CEA, DAM, DIF,
91297
Arpajon Cedex, France
* e-mail: dimitri-alexandre.rochman@psi.ch
Received:
15
September
2017
Received in final form:
24
January
2018
Accepted:
19
March
2018
Published online: 15 May 2018
This paper presents a Bayesian approach based on integral experiments to create correlations between different isotopes which do not appear with differential data. A simple Bayesian set of equations is presented with random nuclear data, similarly to the usual methods applied with differential data. As a consequence, updated nuclear data (cross sections,  , fission neutron spectra and covariance matrices) are obtained, leading to better integral results. An example for 235U and 238U is proposed taking into account the Bigten criticality benchmark.
, fission neutron spectra and covariance matrices) are obtained, leading to better integral results. An example for 235U and 238U is proposed taking into account the Bigten criticality benchmark.
© D.A. Rochman et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
It was recently demonstrated that an uncertainty decrease and non-zero correlation terms between different nuclear data reactions can be obtained when using integral information such as criticality benchmarks [1] (see Refs. [2–4] for other examples). In reference [1], cross-correlation terms between  (emitted neutrons per fission), χ (fission neutron spectra) and σ(n,f) (fission cross section) were calculated in the case of the
(emitted neutrons per fission), χ (fission neutron spectra) and σ(n,f) (fission cross section) were calculated in the case of the  isotope with specific Pu benchmarks in the fast neutron range. Such approach can be useful to lower calculated uncertainties on integral quantities based on nuclear data covariance matrices, without artificially decreasing cross section uncertainties below reasonable and unjustified values. This is appropriate when the propagation of uncertainties from differential data to large-scale systems indicates an apparent discrepancies between uncertainties on measured integral data (neutron multiplication factor, boron concentration, isotopic contents) and the calculated ones. In this reference, the correlation terms between reactions for a specific isotope and the decrease of differential uncertainties were calculated using a simple Bayesian Monte Carlo method. In the present work, the same method is applied (1) to obtain correlation terms this time between different isotopes, and (2) to decrease the uncertainties for important reactions, using again criticality-safety benchmarks. The approach and the equations used in the present work are the same as in [1].
isotope with specific Pu benchmarks in the fast neutron range. Such approach can be useful to lower calculated uncertainties on integral quantities based on nuclear data covariance matrices, without artificially decreasing cross section uncertainties below reasonable and unjustified values. This is appropriate when the propagation of uncertainties from differential data to large-scale systems indicates an apparent discrepancies between uncertainties on measured integral data (neutron multiplication factor, boron concentration, isotopic contents) and the calculated ones. In this reference, the correlation terms between reactions for a specific isotope and the decrease of differential uncertainties were calculated using a simple Bayesian Monte Carlo method. In the present work, the same method is applied (1) to obtain correlation terms this time between different isotopes, and (2) to decrease the uncertainties for important reactions, using again criticality-safety benchmarks. The approach and the equations used in the present work are the same as in [1].
In the following, the case of the 235U and 238U isotopes will be considered and the Bayesian update will be performed using a specific criticality benchmark with high sensitivity to these isotopes: the intermediate metal fast number 7 benchmark, or imf7 (also known as Bigten) [5]. First the method will be recalled in simple terms, then the application with the imf7 benchmark will be presented. The updated benchmark value, cross sections, correlations and uncertainties will be compared to the prior values, thus demonstrating the results for the differential quantities. This is of interest in the context of nuclear data evaluations, where both nominal values and covariance matrices can reflect the present results.
2 Correlation from integral benchmarks
The basic principles of the method were already presented in [1]. We will outline here the major equations. The Bayesian updates of the prior information is obtained using a Monte Carlo process:
-
random nuclear data are produced following specific probability density functions (pdf). Such pdf were obtained as follows: starting from uniform distributions, comparisons between calculations and differential measurements (from EXFOR) were performed. Following the description of reference [6] (and as presented below for integral data), weights are derived from such comparisons and pdf of TALYS model parameters are updated. The next step is to sample from these specific parameter pdf to produce random nuclear data;
-
each random nuclear data is used in the benchmark simulation;
-
the random calculated quantities are compared to the measured one, and;
-
finally each random nuclear data is weighted according to the agreement between the calculated and measured quantities (see below for details on the definition of such weights).
In the present work, the keff value of the imf7 benchmark is used as the only integral quantity: the reported value in [5] is kexp = 1.00450 with an experimental uncertainty of  = 70 pcm. As a prior for the nuclear data, the random 235U and 238U cross sections (and emitted particles and spectra) are obtained from the TENDL-2014 library [7]. The T6 system [8] was used to generate so-called random ENDF-6 and ACE files, containing all necessary random nuclear data. This way, the same file production and processing is followed, based on TALYS and NJOY [8,9]. In the case of the imf7 benchmark, the keff value is very sensitive to the unresolved resonance range [10] and the ENDF-6 files are processed with the PURR module of NJOY. Each ENDF-6 and ACE files are similar in format, but different in content. They are based on sampling of model parameters of the different nuclear models according to specific independent probability distributions (see the TMC, BMC, UMC-B and BFMC methods [6], [11–13] for details). Model parameters are sampled a large number of times (with the index i = 1 … n) to generate full cross sections and other nuclear data quantities for 235U and 238U from 0 to 20 MeV (see for instance [14] for the testing of such file distributions). The sampling between these two isotopes is performed in independent manner, so that no correlation between 235U and 238U can exist other than from the model themselves. The prior correlation matrices for 235U and 238U are simply obtained from the n random files, using the conventional covariance and standard deviation formula.
= 70 pcm. As a prior for the nuclear data, the random 235U and 238U cross sections (and emitted particles and spectra) are obtained from the TENDL-2014 library [7]. The T6 system [8] was used to generate so-called random ENDF-6 and ACE files, containing all necessary random nuclear data. This way, the same file production and processing is followed, based on TALYS and NJOY [8,9]. In the case of the imf7 benchmark, the keff value is very sensitive to the unresolved resonance range [10] and the ENDF-6 files are processed with the PURR module of NJOY. Each ENDF-6 and ACE files are similar in format, but different in content. They are based on sampling of model parameters of the different nuclear models according to specific independent probability distributions (see the TMC, BMC, UMC-B and BFMC methods [6], [11–13] for details). Model parameters are sampled a large number of times (with the index i = 1 … n) to generate full cross sections and other nuclear data quantities for 235U and 238U from 0 to 20 MeV (see for instance [14] for the testing of such file distributions). The sampling between these two isotopes is performed in independent manner, so that no correlation between 235U and 238U can exist other than from the model themselves. The prior correlation matrices for 235U and 238U are simply obtained from the n random files, using the conventional covariance and standard deviation formula.
The n random ACE files are then used in n MCNP6 simulations [15], leading to n values of calculated keff,i with i varying from 1 to n. The comparison between n random calculated keff,i=1...n and the experimental value kexp is performed with the simplified chi-2 Qi values and associated weights wi (here, chi-2 is called Qi to differentiate it from the neutron spectra χ):
 (1)
(1)
 (2)
Such formulation can easily be linked to the usual Bayesian likelihood [13,16]. The weights are then assigned to the corresponding 235U and 238U nuclear data files (for both isotopes together) which lead to keff,i. Considering n random files for each isotopes, there is n2 possible combinations; in the following, we will consider only n combinations such as (1,1), (2,2),…(i,i).
(2)
Such formulation can easily be linked to the usual Bayesian likelihood [13,16]. The weights are then assigned to the corresponding 235U and 238U nuclear data files (for both isotopes together) which lead to keff,i. Considering n random files for each isotopes, there is n2 possible combinations; in the following, we will consider only n combinations such as (1,1), (2,2),…(i,i).
Examples for the weights of the random 235U and 238U nuclear data are presented in Figure 1. In this example, one iteration i corresponds to the use of one specific random file for 235U and another one for 238U. As observed, the distribution of the weights wi strongly varies from values close to 1 (for Qi ≈ 0, indicating a good performance of the random files i) to very small values (almost 0 for large discrepancies between kexp and keff,i). Due to this large range of weights, a large number of random files is necessary to obtain meaningful results. In the case of 7000 random files for each U isotope, about 18% of the weights are higher than 0.01.
The final quantity for a specific benchmark consists of a matrix containing [i, σi(235U), σi(238U), wi] for i = 1 … n, where σi stands for all nuclear data quantities as a function of energy. As previously mentioned, the value of n = 7000 is considered in this work. The correlation ρ(σα, σβ) can be calculated for specific values of the incident neutron energies for σα (Ek) and σβ (Ep). For instance, σα is the fission cross section of 235U and σβ is the capture cross section of 238U, both at a specific energy Ek and Ep, respectively. Considering the vector [i, σi(235U), σi(238U), wi], ρ can be calculated as follows. Using the definition of weighted averages:
 and the definition of the weighted variance/covariance factors:
and the definition of the weighted variance/covariance factors:
 the correlation ρ(σα, σβ) between σα and σβ is given by
the correlation ρ(σα, σβ) between σα and σβ is given by
 (3)Such correlation ρ can be obtained for different EK and Ep, thus defining a full correlation matrix between the same cross section and the same isotope, between different cross sections for the same isotopes, and between isotopes. As quantities in these equations (average cross sections, standard deviations and correlation factors) come from a Monte Carlo process, one has to check their convergence as a function of the iteration number, as presented in Figure 2.
(3)Such correlation ρ can be obtained for different EK and Ep, thus defining a full correlation matrix between the same cross section and the same isotope, between different cross sections for the same isotopes, and between isotopes. As quantities in these equations (average cross sections, standard deviations and correlation factors) come from a Monte Carlo process, one has to check their convergence as a function of the iteration number, as presented in Figure 2.
One can see that in both cases (considering or not weights wi), the final correlation values are different, and the difference is outside the standard errors (defined as  for the non weighted case). As it can be seen on this figure, the non weighted running correlation evolves smoothly with the increasing number of samples, while the weighted running correlation exhibits large jumps for low iteration i where high weight samples are added to the calculation (as seen in [16] showing same kind of behavior).
for the non weighted case). As it can be seen on this figure, the non weighted running correlation evolves smoothly with the increasing number of samples, while the weighted running correlation exhibits large jumps for low iteration i where high weight samples are added to the calculation (as seen in [16] showing same kind of behavior).
In the following, more details will be given on the imf7 benchmark together with the results regarding the prior and posterior information for the uranium isotopes.
 |
Fig. 1 Calculated weights wi for the 7000 random cases considered in this work. The number on the right are the percent of weights within the space defined by the arrows. |
 |
Fig. 2 Example of the running correlation ρ between 235U(n,f) at 510 keV and 238U(n,γ) at 280 keV (top), average cross section (middle) and standard deviation (bottom). The weight comes from the imf7 benchmark. The gray band is the standard error on the correlation factors without weights. |
3 Application to 235U and 238U
The work presented in [1] was limited to the single 239Pu isotope, since it was applied to integral experiments from the PMF subtype (Plutonium Metal Fast) of the ICSBEP collection [5], for which only 239Pu nuclear data dominate the benchmark calculation result. Following the same idea, the imf7 benchmark is selected as its keff is highly impacted by both 235U and 238U.
3.1 The imf7 benchmark
The imf7 benchmark (intermediate enrichment uranium metallic fast number 7), also known as Bigten, is a highly enriched uranium core, surrounded by a massive natural uranium reflector. It is characterized as a fast system, as the majority of the neutron spectrum is above 100 keV. Bigten is a cylindrical assembly with a core composed entirely of fissionable material in metal form. There are three distinct regions: a nearly homogeneous cylindrical central core made of uranium enriched at 10% in 235U, surrounded by a heterogeneous core volume made of natural uranium and highly enriched uranium (93%) and a cylindrical reflector, made of depleted uranium, completely surrounding the core. Figure 3 shows the neutron spectrum averaged over imf7, calculated using MCNP6 with TENDL-14 nuclear data, and average energies for fission and capture are presented in Table 1. It has a typical fast spectrum with an average neutron energy of 530 keV.
This imf7 configuration has long been known by evaluators to be sensitive to nuclear data for both 235U and 238U isotopes. This double dependency is so strong that mixing nuclear data for 235U from one source (e.g. ENDF/B-VII.1 [17]) with data for 238U from another source (e.g. JEFF-3.3) in a imf7 benchmark calculation, results in a poor restitution of the measured keff value. Some examples are presented in Table 2 by repeating the benchmark calculation with different nuclear data evaluations for 235U and 238U.
As observed, if both uranium isotopes come from the same library, the calculated keff is close to the experimental value. On the other hand, a mixture of the library of origin leads to very different calculated keff. These cases can be interpreted as the effective presence of correlated isotopes in current evaluated nuclear data libraries.
 |
Fig. 3 Neutron spectrum of the imf7 ICSBEP benchmark calculated by MCNP6 using TENDL-2014 nuclear data. This spectrum is averaged for the whole benchmark. In the 238U blanket, the average neutron energy is 345 keV, while in the 235U core, it is 580 keV. |
Average neutron energy in keV causing fission or capture in the two main zones of the imf7 benchmark.
Comparison of keff calculation for imf7 by mixing the sources of the evaluations for 235U and 238U. In all cases, the probability tables are included. The statistical uncertainties are about 25 pcm. The reported keff in the ICSBEP database is 1.00450.
3.2 Correlations
By extending the methodology described in reference [1], such cross-isotopes correlations can be rigorously quantified. All combinations of neutron incident energy, observables (cross sections, prompt fission neutron spectra, nubar, etc.), and target isotopes are possible, as illustrated in Figure 4.
Correlation matrices for a selection of cross sections, nubar and pfns in the case of 235U and 238U. Top: correlation without taking into account the imf7 benchmark; bottom: same, but taking into account imf7. See text for details. In each sub-block, the cross sections are presented as a function of the incident neutron energy (the lower-left part corresponds to the lower neutron energy range, whereas the higher-right part corresponds to the higher neutron energy).
The upper panel of Figure 4 shows the full 235U-238U correlation matrix for the prior (unweighted), Total Monte-Carlo (TMC) [11] samples for 235U and 238U, as computed from the TENDL-2014 library. Four blocks are separated by two red lines, each block represents the correlation and cross-correlation for these isotopes: bottom-left: 235U-235U, bottom-right: 235U-238U, top-left: 238U-235U and top-right: 238U-238U. As it can be seen, cross-isotopes correlations between isotopes are zero, since model parameters for both isotopes were independently sampled in this study.
The lower panel shows the full 235U-238U correlation matrix for the TMC samples of 235U and 238U, weighted according to equation (2), where kexp is the experimental value of the imf7 benchmark, and keff,i that derived from the 235U and 238U sampled files, indexed by i. Obviously, that lower panel exhibits cross-isotopes correlations contrary to the upper one, and it also exhibits correlations between different types of observables like those discussed in [1].
Although the TMC treatment allows the constructions of covariance matrices between all the nuclear data observables, the matrices shown in Figure 4 are restricted to the observables which are expected to have a strong influence of keff; hence the (n,p), (n,2n), and other cross sections are not shown in this figure. The color coding of the amplitude of the correlation in Figure 4 reflects four levels of correlations: zero or very low (white), low (lighter blue or red), moderately strong (intermediate blue or red), and very strong (darker blue or red), with red identifying positive correlations, and blue negative ones. The correlations between observables from different isotopes (in the off-diagonal blocks) sit in the low range. The 235U or 238U sub-matrices display some stronger correlations, mostly along the diagonal, but also for observables derived from the optical model potential (total, non elastic and elastic cross sections), highlighting the role played by that model in inducing correlations in nuclear data.
As expected, similarly to the conclusions of references [1,16], a weak negative correlation for the posterior is observed (see Fig. 5 for an enlarged sub-matrix) between the  of 235U and its fission cross section, for energies close to the mean energy of neutrons causing fission in 235U (Tab. 1). This anti-correlation results from
of 235U and its fission cross section, for energies close to the mean energy of neutrons causing fission in 235U (Tab. 1). This anti-correlation results from  and σ(n,f) being two factors in the product describing the neutron source term in the neutronic transport equation: a stronger σ(n,f) is exactly compensated by a weaker
and σ(n,f) being two factors in the product describing the neutron source term in the neutronic transport equation: a stronger σ(n,f) is exactly compensated by a weaker  .
.
The correlation matrix between the 235U capture and fission cross sections (Fig. 6) is harder to interpret, since it exhibits a complex structure. Although the crosses materializing the mean energies leading to fission and capture reactions in the core and blanket regions of the assembly both sit in the weak correlation region of the map (close to the negligible correlations zone (white), there are regions of stronger correlation, both positive and negative, nearby. The moderate positive correlation for neutron energies seen above 500 keV can be understood as 235U(n,f) driving the source term of the neutronic transport equation and 235U(n,γ) being a contributor to the absorption term of that equation. For lower neutron energies, two zones of moderate negative correlation are observed, one for low (E < 200keV) neutron energy inducing fission, and one for low neutron energy inducing capture. That complex structure of the 235U capture and fission correlation might result from the interplay between 235U in the core region (fast spectrum) and the blanket region (slower neutronic spectrum).
From Figure 4, one can also note two important aspects:
-
anti-correlation for 235U between χ and (n,γ): in order to compensate for a higher neutron capture, the fission spectrum becomes harder, thus producing more neutrons at higher energy;
-
especially in the case of 238U, anti-correlation appears in the updated matrices between the inelastic cross sections themselves. Again, this can be understood in order to compensate for the loss of neutrons caused from a specific inelastic cross section (for instance (n,inl)) by another one (for instance (n,inl2)).
In the off-diagonal cross-isotope correlation blocks, a prevalent weak positive correlations can be observed between 235U(n,f) and 238U(n,γ) at energies where the neutronic spectrum is strong (see Fig. 7 for an enlarged sub-matrix). Again, that positive correlation is explained by 235U(n,f) driving the source term and 238U(n,γ) being the other strong contributor to the absorption term of the neutronic transport equation.
A very prevalent weak anti-correlation can also be observed between the fission cross section of 235U and the total elastic cross section of 238U (presented in an enlarged format in Fig. 8). They are anti-correlated since a weaker fission cross section of 235U can be compensated by a more efficient neutron reflector (238U(n,el)), which reflects leaking neutrons back into the 235U core for another attempt to fission 235U.
 |
Fig. 4 Correlation sub-matrix between the |
 |
Fig. 5 As in Figure 4: correlation sub-matrix between the fission and capture cross sections of 235U. The red and black crosses indicate the average energy of the neutron causing fission and capture events in the core and blanket regions, respectively. |
 |
Fig. 6 As in Figure 4: correlation sub-matrix between the fission cross section of 235U and the capture cross section of 238U. The cross indicate the average energy of the neutron causing 235U fission and 238U capture events. |
 |
Fig. 7 As in Figure 4: correlation sub-matrix between the fission cross section of 235U and the elastic cross section of 238U. |
 |
Fig. 8 Comparison between the posterior (weighted), prior (unweighted) and the IAEA standard 235U(n,f) cross section and evaluated uncertainties (the lines denotes the cross sections whereas the bands are the uncertainties). |
3.3 Updated cross sections and variances
The weighting of TMC samples according to equations (1) and (2) not only introduces correlations between observables, but it also leads to modifications of the central values of nuclear data as well as a reduction of the variances of the various nuclear data observables. Such updated cross sections and variances are presented in Figures 9 and 10 and for all considered quantities.
Ratio of cross sections (and  and χ) for the post-adjusted (a posteriori) over the prior. The cross sections,
and χ) for the post-adjusted (a posteriori) over the prior. The cross sections,  and χ are presented from 100 keV to 6 MeV on a logarithmic scale.
and χ are presented from 100 keV to 6 MeV on a logarithmic scale.
The general observation is that the cross sections (including  and χ) are moderately updated (maximum of 1.0% for the 235U(n,inl) cross section) whereas the variances are strongly reduced (see for instance 235U(n,f)). The changes in the posterior cross sections are to some extent depending on the prior uncertainties. If the prior uncertainties are small, the changes will also be small. Therefore the changes presented in Figure 10 can be different for different prior. In the case of 235U, that reduction brings the variance in the same order of magnitude as that of the existing experimental differential data. However, for 238U, the reduced standard deviation is still larger than that of existing differential data: a further Bayesian update with that differential data would further reduce the calculated uncertainty of the 238U
and χ) are moderately updated (maximum of 1.0% for the 235U(n,inl) cross section) whereas the variances are strongly reduced (see for instance 235U(n,f)). The changes in the posterior cross sections are to some extent depending on the prior uncertainties. If the prior uncertainties are small, the changes will also be small. Therefore the changes presented in Figure 10 can be different for different prior. In the case of 235U, that reduction brings the variance in the same order of magnitude as that of the existing experimental differential data. However, for 238U, the reduced standard deviation is still larger than that of existing differential data: a further Bayesian update with that differential data would further reduce the calculated uncertainty of the 238U  (see for instance [18,19] for details).
(see for instance [18,19] for details).
A limited set of cross section uncertainties is strongly affected by the Bayesian update: with a decrease for 235U(n,f), 235U(n,inl), 235U(n,γ), 238U(n,inl), 238U(n,inl) and 238U (n,el) and an increase for 238U(n,inl). One should notice that the (n,inl) cross section for 238U is relatively small, with a maximum at 400 mb, compared to the (n,inl) cross section (with a maximum of 1.5 b). Such change could be explained by statistical fluctuations, but a dedicated study on this effect would be necessary to clarify its origin. The increase of this cross section uncertainty has therefore a limited impact. It is difficult to assess the relative importance of these cross sections in the decrease of the keff uncertainty, but the mentioned reactions are important for the account of neutrons in the energy region of interest.
The value of the 235U posterior fission cross section is modified by a factor as large as 1.003 relatively to that of the prior, and its standard deviation is strongly reduced. When compared with the international cross section standard [19] for the 235U fission cross section (see Fig. 11), their agreement is quite good over en extended energy range: the central values are close (except after the onset of the second chance fission around 0.8 MeV, where the posterior cross section overestimates that of the standard) and the error bars largely overlap. For 238U, the relative variations of the posterior with respect to the prior are less than 1%.
As a final remark, since the Bayesian weighting of samples applies to sets of complete ENDF-6 formatted files (one set including an ENDF-6 file for 235U and a file for 238U), that weighting process produces adjustments and variance reduction for all the observables included in these files, from the inelastic and elastic cross sections, which do play role in the calculation of imf7, to cross sections like (n,p) or (n,α), which are hardly constrained by the benchmark.
 |
Fig. 9 Ratio of cross sections (and |
 |
Fig. 11 Comparison between the posterior (weighted), prior (unweighted) and the IAEA standard 235U(n,f) cross section and evaluated uncertainties (the lines denote the cross sections whereas the bands are the uncertainties). |
3.4 Resulting keff distributions
The final result of the Bayesian weighting process, driven by the experimental kexp of the imf7 benchmark, is the simulated keff distribution, calculated by MCNP6, using the weighted correlated 235U-238U samples, and how it compares to the one calculated with the initial unweighted samples from TENDL-2014. Table 2 shows the averages and standard deviations of the calculated keff distributions, compared with the experimental value, with unweighted sampled labeled as “prior”, and weighted samples labeled as “posterior”. Those distributions of keff are also displayed on Figure 12. In Table 3 and Figure 12, the posterior distribution can be observed to agree very well with the experimental result and its uncertainties, while the average keff resulting from the unweighted prior is lower, with a much wider distribution.
 |
Fig. 12 Prior and posterior distributions of keff for imf7 benchmark. The blue line indicates the experimental value. |
Prior and posterior average keff and uncertainties for four benchmarks. Uncertainties Δk are given in pcm. C/E values are also indicated. The statistical uncertainty for each MCNP6 calculation is in the order of 25 pcm.
4 Discussions
As mentioned in the introduction, the goal of this type of work is to reduce the calculated uncertainties on integral quantities while keeping realistic uncertainties and correlations for the differential data. Additionally, as showen in Table 3 for imf7, the updated 238U and 235U nuclear data provide keff which is in better agreement with the experimental value. Such method can be extended by including more benchmarks in the definition of Qi (and also by including other quantities such as spectra indexes), but prior to the continuation, two tests can be performed. The first one is partially presented in Figures 9 and 10, showing that the updated nuclear data are still in agreement with the differential data (i.e. pointwise cross sections, or pointwise  ). This is not explicitly shown in these figures, but the fact that the updated cross sections are very close to the prior values indicates that the method does not produce very different cross sections compared to the prior. And as it was mentioned, the agreement with the standard cross section is still respected, given the large variances of the TENDL curves.
). This is not explicitly shown in these figures, but the fact that the updated cross sections are very close to the prior values indicates that the method does not produce very different cross sections compared to the prior. And as it was mentioned, the agreement with the standard cross section is still respected, given the large variances of the TENDL curves.
The second test concerns the predictive power of the method: by choosing a benchmark with similar characteristics than imf7, is its calculated keff improved? If this is the case, one can consider that the indications provided by the updated cross sections are general enough to be exported to outside the case of imf7. To answer this question, three additional benchmarks are calculated with the same random 238U and 235U nuclear data files: using or not the weights from imf7. Two of these benchmarks are relatively close to imf7: hmf1 (or Godiva being a metallic sphere of 235U) and imf1-1 (or Jemima, being metallic cylindrical arrangement of 235U). A third benchmark is on purpose chosen to be very different than imf7: it is a thermal system of low-enriches UO fuel rods with a high water-to-fuel ratio: lct6-1. For this benchmark, the modifications of the 238U and 235U nuclear data in the fast neutron range from imf7 are expected to have little impacts on the calculated keff. The results of these calculations are presented in Table 3.
First, the keff values for hmf1, imf1-1 and lct6-1 calculated with weights from imf7 (posterior in Tab. 3), are not in worse agreement with experiment than the ones calculated without weights (prior in Tab. 2). This suggests that weighting random samples according to one given benchmark does not produce a distribution that is only good for that benchmark. Moreover, introducing the imf7-derived weights seems to slightly improve the agreement of all three of our test cases with experimental values, suggesting that the changes due to that weighting carry some real physics and are not just a better local optimization. However, while the weighted imf1-1 and lct6-1 calculation results are within experimental uncertainties, that of hmf1 is still well outside of experimental uncertainties, suggesting that the imf7 specific weighting is missing some of the physics that is essential for the hmf1 case.
Now, looking at the calculated uncertainties for the weighted hmf1 and imf1-1 cases, we observe that their widths are reduced compared to those of the unweighted calculations, suggesting again that imf7-derived weights carry some real physical information. However, the widths resulting from weighted calculations are much larger than experimental uncertainties. In the case of the lct6-1 benchmark, the uncertainties are not reduced: the changes generated at high energy do not impact the uncertainties for this thermal system. This indicates that in the case of a general evaluation of nuclear data, one needs to include benchmarks spanning over a wide energy range.
In order to confirm the conclusions from the above test, it should be repeated on a more extensive set of benchmark cases. The next step in this process would then be to calculate weights from all those benchmark cases, to combine them (maybe through a simple product), and test whether the resulting weighted distribution provides a good restitution of all the experimental benchmark data used to determine those weights (see for instance the work performed in [3,20]).
There is also no reason to restrict the benchmark data used to calculate weights to only keff, and other types of data, like spectral indices or differential measurements, are likely to carry information that constraints nuclear data in a different manner.
5 Conclusion
It has been shown that including integral constraints from experiments that are sensitive to two isotopes introduces effective cross-correlations between the nuclear data of these isotopes. It was demonstrated that it is possible to quantify such cross-correlation between isotopes using an integral benchmark, based on a Bayesian method and a set of random nuclear data. The case under study concerns the 235U and 238U isotopes and the Bigten (imf7) benchmark. Additionally, the updated nuclear data and their covariance matrices lead to a better agreement with the calculated and measured integral data, for the central values and for uncertainties, while keeping the original good agreement with differential data.
This is an extension of the method previously proposed for 239Pu [1] and is a confirmation that such method allows (1) to be part of the evaluation process of nuclear data, and (2) to obtain reasonable integral and differential uncertainties. In the future, the method will be applied taking into account a larger set of integral data and exploring applications below the fast neutron range. Our limited testing is suggesting that weighting with respect to one benchmark experiment does not negatively affect the agreements with other experiments and even improves them slightly. A more extensive testing is needed to confirm that combining weights calculated from different benchmark experiments leads to a weighted sampling that simultaneously accounts for all those benchmarks and their associated uncertainties. Such a combination of weights originating from different benchmarks will be the subject of a forthcoming article.
Like in [1], the present work is at the “proof of concept” stage: the methodology seems to work with a reduced set of integral constraints and the rather simple models used to produce the TENDL-2014 library. In order to produce evaluations of the quality of the best evaluated nuclear data libraries, that method will have to be extended to:
-
include a larger and more representative set of integral experimental constraints, spanning a wide range of neutronic spectra and applications;
-
include integral constraints other than keff in the calculation of weights, include differential constraints as well as international cross sections standards [19] in the calculations of weights;
-
apply that methodology to the more sophisticated models [21–23] used to evaluate the nuclear data of the best international data libraries;
-
completely implementing the above extensions would produce fully updated nuclear data and covariance matrices, including cross-isotopes and cross-observables correlations, following a well defined reproducible scheme. These files should allow for accurate simulation of application, including calculated uncertainties. Such work would then be part of the elaboration of a nuclear data library based on models (for differential data), realistic model parameter distributions and integral constraints, as presented in [24].
References
- D. Rochman, E. Bauge, A. Vasiliev, H. Ferroukhi, Correlation nu-sigma-chi in the fast neutron range via integral information, EPJ Nuclear Sci. Technol. N3, 14 (2017) [CrossRef] [EDP Sciences] [Google Scholar]
- G. Palmiotti, H. Hiruta, M. Salvatores, M. Herman, P. Oblozinsky, M.T. Pigni, Use of Covariance Matrices in a Consistent (Multiscale) Data Assimilation for Improvement of Basic Nuclear Parameters in Nuclear Reactor Applications: from Meters to Femtometers, J. Korean Phys. Soc. 59, 1123 (2011) [Google Scholar]
- M. Salvatores et al., Methods and issues for the combined use of integral experiments and covariance data, Tech. rep., Organization for Economic Co-operation and Development Nuclear Energy Agency (OECD-NEA), WPEC-33. NEA/NSC/WPEC/DOC(2013)445 [Google Scholar]
- C. De Saint Jean, P. Archier, E. Privas, G. Noguere, O. Litaize, P. Leconte, Evaluation of cross section uncertainties using physical constraints: Focus on integral experiment, Nucl. Data Sheets 123, 178 (2015) [CrossRef] [Google Scholar]
- J.B. Briggs Ed., International Handbook of evaluated Criticality Safety Benchmark Experiments, NEA/NSC/DOC(95)03/I (Organization for Economic Co-operation and Development, Nuclear Energy Agency, 2004) [Google Scholar]
- A.J. Koning, Bayesian Monte Carlo method for nuclear data evaluation, Eur. Phys. J. A51, 184 (2015) [Google Scholar]
- A.J. Koning, D. Rochman, J. Kopecky, J. Ch. Sublet, E. Bauge, S. Hilaire, P. Romain, B. Morillon, H. Duarte, S. van der Marck, S. Pomp, H. Sjostrand, R. Forrest, H. Henriksson, O. Cabellos, S. Goriely J. Leppanen, H. Leeb, A. Plompen, R. Mills, TENDL-2014: TALYS-based evaluated nuclear data library ftp://ftp.nrg.eu/pub/www/talys/tendl2014/random.html [Google Scholar]
- A.J. Koning, D. Rochman, Modern nuclear data evaluation with the TALYS code system, Nucl. Data Sheets 113, 2841 (2012) [CrossRef] [Google Scholar]
- R.E. MacFarlane, A.C. Kahler, Methods for processing ENDF/B-VII with NJOY, Nucl. Data Sheets 111, 2739 (2010) [Google Scholar]
- J.Ch. Sublet, R.N. Blomquist, S. Goluoglu, R.E. McFarlane, Unresolved resonance range cross section probability and self shielding factors, CEA report CEA -R-6227 France, 2009 [Google Scholar]
- A.J. Koning, D. Rochman, Towards sustainable nuclear energy: Putting nuclear physics to work, Ann. Nucl. Energy 35, 2024 (2008) [CrossRef] [Google Scholar]
- E. Bauge, P. Dossantos-Uzarralde, Evaluation of the Covariance Matrix of 239Pu Neutronic Cross Sections in the Continuum Using the Backward-Forward Monte-Carlo Method, J. Korean Phys. Soc. 59, 1218 (2011) [CrossRef] [Google Scholar]
-
R. Capote, D.L. Smith, A. Trkov, M. Meghzifene, A new formulation of the Unified Monte Carlo Approach (UMC-B) and cross-section evaluation for the dosimetry reaction 55Mn(n,
 )56Mn, J. ASTM Int. 9, 1 (2012)
[Google Scholar]
)56Mn, J. ASTM Int. 9, 1 (2012)
[Google Scholar]
- P. Helgesson, D. Rochman, H. Sjostrand, E. Alhassan, A.J. Koning, UO Versus MOX: Propagated Nuclear Data Uncertainty for keff, with Burnup, Nucl. Sci. Eng. 177, 321 (2014) [CrossRef] [Google Scholar]
- T. Goorley, MCNP 6.1.1 − Beta release Notes, Los Alamos National Laboratory, Report LA-UR-14-24680, June 2014. [Google Scholar]
- C. De Saint Jean, P. Archier, E. Privas, G. Noguere, On the use of Bayesian Monte-Carlo in evaluation of nuclear data EPJ Web of Conferences, in ND 2016: International Conference on Nuclear Data for Science and Technology, 146, 02007 (2017) [Google Scholar]
- M. Chadwick, M. Herman, P. Oblozinsky, M.E. Dunn, Y. Danon, A.C. Kahler, D.L. Smith, B. Pritychenko, G. Arbanas, R. Arcilla, R. Brewer, D.A. Brown, R. Capote, A.D. Carlson, Y.S. Cho, H. Derrien, K. Guber, G.M. Hale, S. Hoblit, S. Holloway, T.D. Johnson, T. Kawano, B.C. Kiedrowski, H. Kim, S. Kunieda, N.M. Larson, L. Leal, J.P. Lestone, R.C. Little, E.A. McCutchan, R.E. MacFarlane, M. MacInnes, C.M. Mattoon, R.D. McKnight, S.F. Mughabghab, G.P.A. Nobre, G. Palmiotti, A. Palumbo, M.T. Pigni, V.G. Pronyaev, R.O. Sayer, A.A. Sonzogni, N.C. Summers, P. Talou, I.J. Thompson, A. Trkov, R.L. Vogt, S.C. van der Marck, A. Wallner, M.C. White, D. Wiarda, P.G. Young, ENDF/B-VII.1 Nuclear Data for Science and Technology: Cross Sections, Covariances, Fission Product Yields and Decay Data, Nucl. Data Sheets 112, 2887 (2011) [CrossRef] [Google Scholar]
- A.J. Plompen, T. Kawano, Inelastic Scattering and Capture Cross-section Data of Major Actinides in the Fast Neutron Region, Summary Report (IAEA Nuclear Data Section, Vienna, INDC(NDS-0597, 2012) [Google Scholar]
- A.D. Carlson, V.G. Pronyaev, D.L. Smith, N.M. Larson, Zhenpeng Chen, G.M. Hale, F.-J. Hambsch, E.V. Gai, Soo-Youl Oh, S.A. Badikov, T. Kawano, H.M. Hofmann, H. Vonach, S. Tagesen, International Evaluation of Neutron Cross Section Standards, Nucl. Data Sheets 110, 3215 (2009) [CrossRef] [Google Scholar]
- G. Palmiotti, M. Salvatores, K. Yokoyama, Methods and Approaches to Provide Feedback from Nuclear and Covariance Data Adjustment for Improvement of Nuclear Data Files, Organization for Economic Co-operation and Development Nuclear Energy Agency (OECD-NEA), WPEC-39, NEA/NSC/R 2016, (2017) [Google Scholar]
- M. Sin, R. Capote, M.W. Herman, A. Trkov, Modeling neutron-induced reactions on 232−237U from 10 keV to 30 MeV, Nucl. Data Sheets 139, 138 (2017) [Google Scholar]
- P. Romain, B. Morillon, H. Duarte, Buyères-le-Châtel evaluation of actinides with th TALYS code: the fission channel, Nucl. Data Sheets 131, 222 (2016) [CrossRef] [EDP Sciences] [Google Scholar]
- E. Bauge, G. Bélier, J. Cartier, A. Chatillon, J.M. Daugas, J.P. Delaroche, P. Dossantos-Uzarralde, H. Duarte, N. Dubray, M. Ducauze-Philippe, L. Gaudefroy, G. Gosselin, T. Granier, S Hilaire, Huu-Tai P. Chau, J.M. Laborie, B. Laurent, X. Ledoux, C. Le Luel, V. Méot, P. Morel, B. Morillon, O. Roig, P. Romain, J. Taieb, C. Varignon, N. Authier, P. Casoli, B. Richard, Coherent investigation of nuclear data at CEA DAM: Theoretical models, experiments and evaluated data, Eur. Phys. J. A 48, 113 (2012) [CrossRef] [EDP Sciences] [Google Scholar]
- E. Bauge, M. Dupuis, S. Hilaire, S. Péru, A.J. Koning, D. Rochman, S. Goriely, Nucl. Data Sheets 118, 32 (2014) [CrossRef] [Google Scholar]
Cite this article as: Dimitri A. Rochman, Eric Bauge, Alexander Vasiliev, Hakim Ferroukhi, Gregory Perret, Nuclear data correlation between different isotopes via integral information, EPJ Nuclear Sci. Technol. 4, 7 (2018)
All Tables
Average neutron energy in keV causing fission or capture in the two main zones of the imf7 benchmark.
Comparison of keff calculation for imf7 by mixing the sources of the evaluations for 235U and 238U. In all cases, the probability tables are included. The statistical uncertainties are about 25 pcm. The reported keff in the ICSBEP database is 1.00450.
Prior and posterior average keff and uncertainties for four benchmarks. Uncertainties Δk are given in pcm. C/E values are also indicated. The statistical uncertainty for each MCNP6 calculation is in the order of 25 pcm.
All Figures
 |
Fig. 1 Calculated weights wi for the 7000 random cases considered in this work. The number on the right are the percent of weights within the space defined by the arrows. |
| In the text | |
 |
Fig. 2 Example of the running correlation ρ between 235U(n,f) at 510 keV and 238U(n,γ) at 280 keV (top), average cross section (middle) and standard deviation (bottom). The weight comes from the imf7 benchmark. The gray band is the standard error on the correlation factors without weights. |
| In the text | |
 |
Fig. 3 Neutron spectrum of the imf7 ICSBEP benchmark calculated by MCNP6 using TENDL-2014 nuclear data. This spectrum is averaged for the whole benchmark. In the 238U blanket, the average neutron energy is 345 keV, while in the 235U core, it is 580 keV. |
| In the text | |
 |
Fig. 4 Correlation sub-matrix between the |
| In the text | |
 |
Fig. 5 As in Figure 4: correlation sub-matrix between the fission and capture cross sections of 235U. The red and black crosses indicate the average energy of the neutron causing fission and capture events in the core and blanket regions, respectively. |
| In the text | |
 |
Fig. 6 As in Figure 4: correlation sub-matrix between the fission cross section of 235U and the capture cross section of 238U. The cross indicate the average energy of the neutron causing 235U fission and 238U capture events. |
| In the text | |
 |
Fig. 7 As in Figure 4: correlation sub-matrix between the fission cross section of 235U and the elastic cross section of 238U. |
| In the text | |
 |
Fig. 8 Comparison between the posterior (weighted), prior (unweighted) and the IAEA standard 235U(n,f) cross section and evaluated uncertainties (the lines denotes the cross sections whereas the bands are the uncertainties). |
| In the text | |
 |
Fig. 9 Ratio of cross sections (and |
| In the text | |
 |
Fig. 10 Same as Figure 9 but for the calculated uncertainties (standard deviations). |
| In the text | |
 |
Fig. 11 Comparison between the posterior (weighted), prior (unweighted) and the IAEA standard 235U(n,f) cross section and evaluated uncertainties (the lines denote the cross sections whereas the bands are the uncertainties). |
| In the text | |
 |
Fig. 12 Prior and posterior distributions of keff for imf7 benchmark. The blue line indicates the experimental value. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.