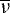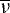| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
|
|
|---|---|---|
| Article Number | 35 | |
| Number of page(s) | 6 | |
| Section | Covariance Evaluation Methodology | |
| DOI | https://doi.org/10.1051/epjn/2018011 | |
| Published online | 14 November 2018 | |
https://doi.org/10.1051/epjn/2018011
Regular Article
Cross-observables and cross-isotopes correlations in nuclear data from integral constraints
1
CEA, DAM, DIF,
91297
Arpajon, France
2
Laboratory for Reactor Physics Systems Behaviour, Paul Scherrer Institut,
Villigen, Switzerland
* e-mail: eric.bauge@cea.fr
Received:
31
October
2017
Received in final form:
16
January
2018
Accepted:
4
May
2018
Published online: 14 November 2018
Most recent evaluated nuclear data files exhibit excellent integral performance, as shown by the very good agreement between experimental and calculated keff values over a wide range of benchmark integral experiments. However, the propagation of the uncertainties associated with those nuclear data to integral observables, generally produces calculated distribution which are much (3–5 times) wider than the experimental uncertainties. Reducing the variances of the evaluated data to achieve consistency at the integral level would lead to unreasonably narrow variances in the light of differential experimental data. One way of solving that paradox could be to allow, for different observables like fission cross-sections (σf), the prompt fission neutron spectra (χ), and the average multiplicity of fission neutrons (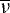 ) to be correlated in a Bayesian-like, Total Monte-Carlo approach, under constraints from integral experiments from the ICSBEP (International International Criticality Safety Benchmark Evaluation Project) benchmark compilation. Future developments will be highlighted and restrictions imposed by the current formatting of nuclear data will be discussed.
) to be correlated in a Bayesian-like, Total Monte-Carlo approach, under constraints from integral experiments from the ICSBEP (International International Criticality Safety Benchmark Evaluation Project) benchmark compilation. Future developments will be highlighted and restrictions imposed by the current formatting of nuclear data will be discussed.
© E. Bauge and D. A. Rochman, published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
There seems to be a contradiction between capacity of current generation nuclear data libraries to accurately account for a wide range of integral benchmarks like [1] and the width exhibited by propagated nuclear data uncertainties which are much wider than the experimental uncertainties. This contradiction results from the large difference between the orders of magnitude of experimental errors for differential or integral experiment. While cross-sections are typically measured with precisions of the order of a few 10% down to about 1% (for the fission cross-sections of the international standards [2], for example), the average prompt fission neutron energies are experimentally known within a few percent, and the prompt fission neutron average multiplicities are not experimentally known better than 1% for neutron induced fission, integral quantities are typically measured with a precision between 0.1% and 0.3%. Therefore, to achieve good integral performance, some calibration is performed. While the σf, χ and (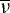 ) evaluated values are usually evaluated independently, using only differential data as experimental constraints, the assembly of nuclear data files by the international libraries is performed using integral constraints: the independent σ, χ and
) evaluated values are usually evaluated independently, using only differential data as experimental constraints, the assembly of nuclear data files by the international libraries is performed using integral constraints: the independent σ, χ and 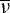 datasets are combined, and only the combinations that account well for the selected integral experiments are retained. This calibration process is in essence of Bayesian inspiration: keeping (giving high likelihood weights) the combinations that account well for experimental evidences, and discarding (giving low likelihood weights) the combinations that fail to reproduce experimental evidences. Yet, as of today, the existence of this process is not widely acknowledged. The uncertainties associated with nuclear data, on the other hand, essentially reflect the differential data, and do not usually account for the above calibration process. For this reason, when such uncertainties are propagated to integral experiment simulations, the calculated uncertainty is much wider than the measured uncertainty, whereas the central value is usually well predicted, thanks to the above calibration process.
datasets are combined, and only the combinations that account well for the selected integral experiments are retained. This calibration process is in essence of Bayesian inspiration: keeping (giving high likelihood weights) the combinations that account well for experimental evidences, and discarding (giving low likelihood weights) the combinations that fail to reproduce experimental evidences. Yet, as of today, the existence of this process is not widely acknowledged. The uncertainties associated with nuclear data, on the other hand, essentially reflect the differential data, and do not usually account for the above calibration process. For this reason, when such uncertainties are propagated to integral experiment simulations, the calculated uncertainty is much wider than the measured uncertainty, whereas the central value is usually well predicted, thanks to the above calibration process.
In reference [3], cross-observables correlations between the fission cross-section (σf), the prompt fission neutron spectra (χ), and the average multiplicity of fission neutrons (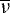 ), resulting from the use integral constraints were quantified using a Bayesian update of prior information obtained in a Monte-Carlo sampling of nuclear model parameters, inspired by the Total Monte-Carlo (TMC) approach [4]. In this first application, Monte-Carlo samples of the 239Pu nuclear data file, were weighted according to the agreement between MCNP [5] simulations of Plutonium-Metal-Fast (PMF) configurations from [1] and the corresponding experimental values.
), resulting from the use integral constraints were quantified using a Bayesian update of prior information obtained in a Monte-Carlo sampling of nuclear model parameters, inspired by the Total Monte-Carlo (TMC) approach [4]. In this first application, Monte-Carlo samples of the 239Pu nuclear data file, were weighted according to the agreement between MCNP [5] simulations of Plutonium-Metal-Fast (PMF) configurations from [1] and the corresponding experimental values.
In reference [6], the Bayesian MC approach was applied to quantify the cross-isotopes correlations resulting from the use of an integral experimental constraint that exhibit strong sensitivity to more than one isotope. In that case, the IMF7 (Intermediate enrichment-Metal-Fast, “Bigten”) ICSBEP benchmark, was used. It is known to be sensitive to nuclear data for both 235U and 238U isotopes. As could be expected, using IMF7 as an integral constraint to calculate the Bayesian weights (likelihood), results in the appearance of cross-isotopes correlations between 235U and 238U nuclear data.
After detailing the methodology (Sect. 2) and illustrating the results and their implications with examples drawn from reference [3] (Sect. 3) and reference [6] (Sect. 4), in Section 5, we layout plans for future work and in Section 6, we contribute to the ongoing debate on whether integral constraints should be used for evaluating nuclear data in the context of a general purpose library.
2 Bayesian TMC with integral constraints
The basic principles of the methodology are already detailed in references [3,6] and we will only briefly recall the main ideas of the Bayesian TMC approach. The TMC approach [4] makes use of the TALYS code system T6 [7] to sample nuclear model parameters, calculate observables, generate ENDF-6 formatted files, and process them into ACE files, generating a sampling of 10 000 nuclear data files ready to be fed into the MCNP Monte-Carlo neutronics simulation code. These 10 000 nuclear data files are then used to simulate integral experiments and the calculated integral observables (the effective neutron multiplication coefficient keff, in the present case) are compared to the corresponding experimental values. For the ith sample, the keff,i value is computed and compared to the experimental kexp in a simple chi–2 formula:
 (1)
where Δk is the uncertainty of the experimental measurement. The associated weight wi is computed using the usual Bayesian likelihood formula:
(1)
where Δk is the uncertainty of the experimental measurement. The associated weight wi is computed using the usual Bayesian likelihood formula:
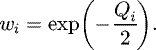 (2)For each observable quantity σα, indexed by the α label, its realization for the ith sample is denoted σα,i. Using the definition of weighted averages:
(2)For each observable quantity σα, indexed by the α label, its realization for the ith sample is denoted σα,i. Using the definition of weighted averages:
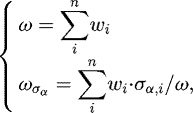 and the definition of the weighted variance/covariance factors:
and the definition of the weighted variance/covariance factors:
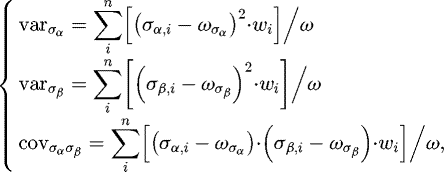 the correlation ρ(σα, σβ) between the σα and σβ observables is given by
the correlation ρ(σα, σβ) between the σα and σβ observables is given by
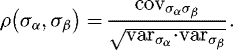 (3)Here, the α and β indices denote both the type of observable (ex: fission cross-section, capture cross-section,
(3)Here, the α and β indices denote both the type of observable (ex: fission cross-section, capture cross-section,  , etc.) and the incident neutron energy E. Therefore ρ(σα, σβ) can express correlation between different observables for different neutron incident energies (for example between the fission cross-section for a 1 MeV incident neutron and the
, etc.) and the incident neutron energy E. Therefore ρ(σα, σβ) can express correlation between different observables for different neutron incident energies (for example between the fission cross-section for a 1 MeV incident neutron and the  for a 500 keV neutron). The convergence of the calculation of means, variances and correlations with a sample size of 10 000 is discussed in [6].
for a 500 keV neutron). The convergence of the calculation of means, variances and correlations with a sample size of 10 000 is discussed in [6].
3 239Pu correlation from PMFs
The first application of Bayesian TMC with integral constraints was to quantify the cross-observables correlations in the 239Pu evaluated nuclear data files, stemming from the use of integral benchmarks from the PMF section of the ICSBEP [1] benchmark compilation. This first example was focused on correlations between the fission cross-section σf, the prompt fission neutron spectrum χ and the average number of prompt fission neutrons 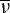 .
.
The correlation matrix between the three σf, χ, and 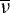 observables resulting from the Bayesian weighting of TMC samples according to the differences between the calculated and experimental keff values, for a selection of nine PMF integral benchmarks, is shown in Figure 1.
observables resulting from the Bayesian weighting of TMC samples according to the differences between the calculated and experimental keff values, for a selection of nine PMF integral benchmarks, is shown in Figure 1.
Examining Figure 1 reveals that weighting the samples according to integral experimental constraints produces sizable correlations in the off-diagonal quadrants. For example, the fission cross-section and 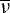 exhibit negative correlations (about −0.2) for energies where most fission occurs in PMFs (between 0.5 and 2 MeV). Negative correlations between σf and χ, and
exhibit negative correlations (about −0.2) for energies where most fission occurs in PMFs (between 0.5 and 2 MeV). Negative correlations between σf and χ, and 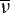 and χ also occur but are weaker. This negative correlation results from the source term of the neutronic transport equation being a product of the three σf, χ,
and χ also occur but are weaker. This negative correlation results from the source term of the neutronic transport equation being a product of the three σf, χ, 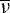 observables. Changing one factor in one direction can be compensated by changing another factor in the other direction by the same relative amount, leaving the source term unchanged. That compensation is being used in calibrating nuclear data libraries so that simulations performed with them are in good agreement with experimental integral data. However, since only central values are calibrated, propagating the nuclear data files uncertainties towards the integral observables produces keff distributions that are much too wide as illustrated by the red histograms of Figure 2.
observables. Changing one factor in one direction can be compensated by changing another factor in the other direction by the same relative amount, leaving the source term unchanged. That compensation is being used in calibrating nuclear data libraries so that simulations performed with them are in good agreement with experimental integral data. However, since only central values are calibrated, propagating the nuclear data files uncertainties towards the integral observables produces keff distributions that are much too wide as illustrated by the red histograms of Figure 2.
Conversely, using weighted samples produces keff distributions (in gray in Fig. 2) that closely match the experimental values and their uncertainties.
Since the above example constitutes only a limited test of Bayesian TMC applied to integral constraints (only nine benchmarks of the same “family”), it is only an illustration that it should possible to propagate nuclear data and its uncertainties into neutronics simulation and obtain distributions of keff that agree with experimental data and its uncertainties. In order to be more than an illustration the above work should be extended to a wider set of benchmark experiments, with different neutronic spectra, and even to integral observables other that those relevant for criticality.
 |
Fig. 1 Posterior correlation matrix for 239Pu |
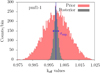 |
Fig. 2 Prior (unweighted, in red) and posterior (weighted, in gray) distributions for the PMF1 and benchmark. The blue lines indicate the experimental values and their uncertainties. |
4 235U-238U correlations from IMF7
In reference [6], the work of [3] was extended to cross-isotopes correlations induced by using integral constraints that are highly sensitive to nuclear data for more than one isotope. More precisely, the IMF7 (Intermediate enrichment-Metallic-Fast or “Bigten”) benchmark was used since it exhibits strong sensitivity to both 235U and 238U. That ICSBEP [1] benchmark describes a critical assembly constituted by a highly enriched 235U surrounded by a massive depleted uranium reflector. That specific configuration is known by evaluator to be especially difficult to account for in neutronics simulations, since it is sensitive to both 235U and 238U. That double sensitivity is demonstrated when one tries to mix 235U and 238U nuclear data files from different libraries as it is done in Table 1.
While calculations performed with 235U and 238U files from the same source (either ENDF/B-VII.1 [8] or JEFF3.3) produce a good description of the experimental keff value (1.00450 ± 0.00070), the calculations done with mixed sources are more that 2-σ away from the experimental value. This is a demonstration that cross-isotopes correlations are present in existing evaluated nuclear data libraries, probably because once more, only the “good” combination of 235U and 238U files was retained in libraries.
We then use the Bayesian TMC with integral constraints to quantify the cross-isotopes correlations resulting from the use of the IMF7 benchmark as an experimental constraint in equation (1). Figure 3 displays the resulting correlation matrix. All combinations of neutron incident energy, observables (cross-sections, prompt fission neutron spectra, nubar, etc.), and target isotopes are possible.
Figure 3 shows the full 235U-238U correlation matrix for the TMC samples of 235U and 238U, weighted according to equation (2), where k is the experimental value of the IMF7 benchmark, and k that derived from the 235U and 238U sampled files, indexed by i. Four blocks are separated by two red lines. Each block represents the correlation and cross-correlation for these isotopes: bottom-left: 235U-235U, bottom-right: 235U-238U, top-left: 238U-235U and top-right: 238U-238U. Cross-isotopes correlations (in the off-diagonal blocks) are obviously present on this figure, but it also shows cross-observables correlations like those discussed in Section 3. The color coding of the amplitude of the correlation in Figure 3 reflects four levels of correlations: zero or very low (white), low (lighter blue or red), moderately strong (intermediate blue or red), and very strong (darker blue or red), with red identifying positive correlations, and blue negative ones.
The correlations between observables from different isotopes (in the off-diagonal blocks) sit in the low range, whereas the 235U or 238U sub-matrices display some stronger correlations, mostly along the diagonal. The 235U fission cross-section is involved in a large fraction of cross-isotopes correlations, exhibiting negative correlations with the 238U 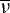 , elastic, and total cross-sections, and positive correlations with the 238U capture, inelastic and non-elastic cross-sections. The 235U capture cross-section is also negatively correlated with the 238U capture cross-section. Some of the cross-isotopes correlations like that between the 235U fission cross section and the 238U elastic cross-section have no justification in nuclear physics and stem only from the use of the IMF7 keff integral constraint: higher 238U elastic cross-sections make a more efficient neutron reflector, sending more leaking neutrons back to the core for another attempt at fissioning 235U.
, elastic, and total cross-sections, and positive correlations with the 238U capture, inelastic and non-elastic cross-sections. The 235U capture cross-section is also negatively correlated with the 238U capture cross-section. Some of the cross-isotopes correlations like that between the 235U fission cross section and the 238U elastic cross-section have no justification in nuclear physics and stem only from the use of the IMF7 keff integral constraint: higher 238U elastic cross-sections make a more efficient neutron reflector, sending more leaking neutrons back to the core for another attempt at fissioning 235U.
Examining the average of the weighted (posterior) observables distributions for both 235U and 238U reveals that changes relative to the prior unweighted averages are small (typically less than 1%). For example the relative change of the 235U fission cross section is of the order of 0.3%, from prior to posterior. Looking at the width (standard deviation) of the weighted (posterior) observables also reveals small relative changes with respect to their unweighted (prior) values: standard deviation are typically reduced by a few percent, some observables like 235U fission or 238U elastic cross-sections exhibiting larger reductions (7%–13% and 8%, respectively). The changes induced by the use of the IMF7 integral constraint do not dramatically affect the average values or the widths of the observables distributions.
However, despite those modest changes to the averages and widths, using the posterior (weighted) distribution to compute the IMF7 keff value yields a very good agreement (1.00446) with the IMF7 experimental value (1.00450 ± 0.00070). The width of the calculated keff distribution (0.00071) also matches the experimental uncertainty. This agreement highlights the important role played by the cross-isotopes and cross-observables correlations resulting from the use of an integral constraint.
Finally, in [6], some tests were performed to find out whether the correlations induced by the use of the IMF7 integral constraint are specific to that benchmark or have some more general value. For that purpose the posterior distribution obtained from the IMF7 constrained was used to calculate a few other benchmarks from the ICSBEP collection: HMF1 (“GODIVA”), IMF1 (“Jemima”) and LCT7. While the first two are fast spectrum benchmarks like IMF7, the last one is a thermal spectrum benchmark, and therefore is expected to exhibit very different sensitivities to nuclear data. For all three benchmarks, using the IMF7 posterior improves agreement with experiment compared with a calculation performed with the unweighted prior. However, the agreement for the three extra configurations is not as good as that of IMF7, suggesting that, while the IMF7 constraint carries some information that is relevant for the HMF1, IMF1 and LCT7 configurations, it still misses some other information that is specific to those benchmarks.
Scanning the widths of the calculated keff distributions for the three extra configurations suggests similar conclusions: the widths of the keff distributions calculated using the IMF7 posterior are reduced compared with the ones calculated using the prior, but they are still too wide to account for the experimental uncertainties.
The above last exercise, naturally leads to the next step of our work: combining weights from several different benchmarks configurations to find out whether a good compromise between those different constraints is reachable.
Comparison of keff calculation for IMF7 by mixing the sources of the evaluations for 235U and 238U. In all cases, the probability tables are included. The statistical uncertainties are about 25 pcm.
 |
Fig. 3 Posterior (weighted) correlation matrices for a selection of cross-sections, nubar and pfns in the case of 235U and 238U, using IMF7 experimental keff value as a constraints in the Bayesian TMC process. In each sub-block, the cross-sections are presented as a function of the incident neutron energy. |
5 Summary
Let us first stress that the above studies are presently at the “proof of concept” stage. The posterior distributions resulting from use of the Bayesian TMC with integral constraints are not candidates for inclusion in evaluated nuclear data libraries, but they are good illustrations of the effect of cross-observables and cross-isotopes correlations in evaluated data files. The Bayesian TMC with integral constraints even allows to rigorously quantify such correlations. It was also demonstrated, in the few studied cases, that the resulting weighted nuclear data files produce keff distribution widths which are comparable to the experimental uncertainties.
The next step will attempt to combine constraints from different benchmarks (with different neutronic spectra, integral observables other than keff, etc.) in order to find out whether such a compromise is achievable. Then, in order to go past the proof of concept stage, differential and integral constraints will have to be combined, and better models (for example for the fission channel) will have to be used. Completely implementing the above extensions would produce fully updated nuclear data and covariance matrices, including cross-isotopes and cross-observables correlations, following a well-defined reproducible scheme. These files should allow for accurate simulation of application, including calculated uncertainties. Such work would then be part of the elaboration of a nuclear data library based on models (for differential data), realistic model parameter distributions and integral constraints, as presented in [9].
Finally, as of today, the cross-observables and cross-isotopes correlations can neither be stored in the existing legacy ENDF-6 format, nor be processed by current nuclear data processing tools. A short-term solution consists in using the TMC approach of storing samples of evaluated data files and their associated weights, but that solution implies a lot of data storage and a heavy computational burden to compute simulations results for large sample sizes. A long-term solution will be to adopt an better storage format and adapt the processing tools to this new type of correlation data.
6 Discussion on the use of integral constraints in covariances
The existence of the Bayesian TMC with integral constraints tool to rigorously quantify correlations stemming from integral constraints, does not automatically implies that such correlations should be included in general purpose nuclear data libraries.
On the one hand, nuclear data users are asking for data that accurately describes their experiments, including the measured uncertainties. Using correlations like those produced by the Bayesian TMC method might help achieving that result.
On the other hand, there is still the question of whether those correlation are physical, and sufficiently general to be included in a general purpose file. Another way of asking this question is: “Are these correlations only accounting for error compensations in a restricted application perimeter ?”
The answer is not clear cut, and the issue is further obscured by the presence of some integral calibrations in present libraries (the paper describing the ENDF/B-VIII.0 [10] evaluated nuclear data library explicitely acknowledges the calibration of the 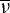 observable for major actinides in order “to optimize keff criticality”). Those integral calibrations are responsible for the good integral performance of these libraries (for example the “right”
observable for major actinides in order “to optimize keff criticality”). Those integral calibrations are responsible for the good integral performance of these libraries (for example the “right” 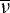 value is selected from its uncertainty band to allow for a good restitution of criticality benchmarks, or the “right” 235U-238U combination is selected for the IMF7 benchmark). That presence also leads to the apparent contradiction of central keff values being calculated essentially within 1- or 2-σ of the experimental uncertainties, whereas the propagated evaluated uncertainties produce much wider distributions.
value is selected from its uncertainty band to allow for a good restitution of criticality benchmarks, or the “right” 235U-238U combination is selected for the IMF7 benchmark). That presence also leads to the apparent contradiction of central keff values being calculated essentially within 1- or 2-σ of the experimental uncertainties, whereas the propagated evaluated uncertainties produce much wider distributions.
Depending on one's point of view, using integral correlations to evaluate uncertainties can either be viewed as the problem or the cure. There seems to be an inherent contradiction between reducing error compensations and reducing the widths of predicted keff distributions: it is possible to achieve either of them, but doing both at the same time still seems to elude us.
A choice has to be made.
Such a choice faces strong opinions on both sides of the argument. Some rightfully insist that general purpose libraries should remain general and be consistent with differential data. Consequently, they strongly oppose the inclusions of correlation derived from integral information into general purpose evaluated data files. The other side rightfully stresses the contradiction between very good predicted criticality and the associated large predicted uncertainties. They imply that unquantified correlations stemming from integral information are present in existing general purpose evaluated nuclear data files. At the present time, it seems difficult to simultaneously satisfy both sides. It is clear that labeling libraries with their proper names, as either “general purpose” or “adjusted”, is a step towards solving that question. However, even criteria for labeling are not presently completely agreed on. That debate is still ongoing, as evidenced by the questions asked in Section 4 of reference [10].
Author contributions statement
All the authors were involved in the preparation of the manuscript. All the authors have read and approved the final manuscript.
References
- J.B. Briggs Ed., International Handbook of evaluated Criticality Safety Benchmark Experiments, NEA/NSC/DOC(95)03/I (Organization for Economic Co-operation and Development, Nuclear Energy Agency, 2004) [Google Scholar]
- A.D. Carlson, V.G. Pronyaev, D.L. Smith, N.M. Larson, Zhenpeng Chen, G.M. Hale, F.-J. Hambsch, E.V. Gai, Soo-Youl Oh, S.A. Badikov, T. Kawano, H.M. Hofmann, H. Vonach, S. Tagesen, International evaluation of neutron cross section standards, Nucl. Data Sheets 110, 3215 (2009) [CrossRef] [Google Scholar]
- D. Rochman, E. Bauge, A. Vasiliev, H. Ferroukhi, Correlation nu-sigma-chi in the fast neutron range via integral information, EPJ Nuclear Sci. Technol. 3, 14 (2017) [CrossRef] [EDP Sciences] [Google Scholar]
- A.J. Koning, D. Rochman, Towards sustainable nuclear energy: putting nuclear physics to work, Ann. Nucl. Energy 35, 2024 (2008) [CrossRef] [Google Scholar]
- T. Goorley, MCNP 6.1.1 −Beta release Notes, Report LA-UR-14-24680 (Los Alamos National Laboratory, 2014) [Google Scholar]
- D. Rochman, E. Bauge, A. Vasiliev, H. Ferroukhi, G. Perret, Nuclear data correaltion between isotopes via integral information, EPJ Nucl. Sci. Technol. 4, 7 (2018) [CrossRef] [EDP Sciences] [Google Scholar]
- A.J. Koning, D. Rochman, Modern nuclear data evaluation with the TALYS code system, Nucl. Data Sheets 113, 2841 (2012) [CrossRef] [Google Scholar]
- M. Chadwick, M. Herman, P. Oblozinsky, M.E. Dunn, Y. Danon, A.C. Kahler, D.L. Smith, B. Pritychenko, G. Arbanas, R. Arcilla, R. Brewer, D.A. Brown, R. Capote, A.D. Carlson, Y.S. Cho, H. Derrien, K. Guber, G.M. Hale, S. Hoblit, S. Holloway, T.D. Johnson, T. Kawano, B.C. Kiedrowski, H. Kim, S. Kunieda, N.M. Larson, L. Leal, J.P. Lestone, R.C. Little, E.A. McCutchan, R.E. MacFarlane, M. MacInnes, C.M. Mattoon, R.D. McKnight, S.F. Mughabghab, G.P.A. Nobre, G. Palmiotti, A. Palumbo, M.T. Pigni, V.G. Pronyaev, R.O. Sayer, A.A. Sonzogni, N.C. Summers, P. Talou, I.J. Thompson, A. Trkov, R.L. Vogt, S.C. van der Marck, A. Wallner, M.C. White, D. Wiarda, P.G. Young, ENDF/B-VII.1 Nuclear data for science and technology: cross sections, covariances, fission product yields and decay data, Nucl. Data Sheets 112, 2887 (2011) [CrossRef] [Google Scholar]
- E. Bauge, M. Dupuis, S. Hilaire, S. Péru, A.J. Koning, D. Rochman, S. Goriely, Nucl. Data Sheets 118, 32 (2014) [CrossRef] [Google Scholar]
- D.A. Brown, M.B. Chadwick, R. Capote, A.C. Khaler, A. Trkov, M.H. Herman, A.Z. Sonzogni, Y, Danon, A.D. Carlson, M. Dunn, D.L. Smith, G, M. Hale, G. Arbanas, R. Arcilla, C.R. Bates, B. Beck, B. Becker, F. Brown, J. Conlin, D.E. Cullen, M.A. Descale, R. Firestone, K.H. Guber, A.I. Hawari, J. Holmes, T.D. Johnson, T. Kawano, B.C. Kerdrowski, A.J. Koning, S. Kopecky, L. Leal, J. Lestone, C. Lubitz, J.I. Marques-Damian, C. Mattoon, E.A. McCuchan, S. Mughabghab, P. Navratil, D. Neudecker, G.P.A. Nobre, G, Nogere, M. Paris, M.T. Pigni, A. Plompen, B. Pritchenko, V.G. Pronayev, D. Roubstov, D. Rochman, P. Romano, P. Schillebeckx, S. Simakov, M. Sin, I. Sirakov, B. Sleaford, V. Sobes, E.S. Soukhovitski, I. Stetcu, P. Talou, I. Thompson, S.V.d. Marck, D. Wiarda, M. White, J.L. Wormald, R.Q. Wright, M. Zerkle, G. Zerovik, Y. Zhu, ENDF/B-VIII.0: the 8th major release of the nuclear data reaction library with CIELO-project corss sections, new standards and thermal scattering data, Nucl. Data. Sheets 148, 1 (2018) [Google Scholar]
Cite this article as: Eric Bauge, Dimitri A. Rochman, Cross-observables and cross-isotopes correlations in nuclear data from integral constraints, EPJ Nuclear Sci. Technol. 4, 35 (2018)
All Tables
Comparison of keff calculation for IMF7 by mixing the sources of the evaluations for 235U and 238U. In all cases, the probability tables are included. The statistical uncertainties are about 25 pcm.
All Figures
 |
Fig. 1 Posterior correlation matrix for 239Pu |
| In the text | |
 |
Fig. 2 Prior (unweighted, in red) and posterior (weighted, in gray) distributions for the PMF1 and benchmark. The blue lines indicate the experimental values and their uncertainties. |
| In the text | |
 |
Fig. 3 Posterior (weighted) correlation matrices for a selection of cross-sections, nubar and pfns in the case of 235U and 238U, using IMF7 experimental keff value as a constraints in the Bayesian TMC process. In each sub-block, the cross-sections are presented as a function of the incident neutron energy. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.