| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
|
|
|---|---|---|
| Article Number | 14 | |
| Number of page(s) | 8 | |
| Section | Applied Covariances | |
| DOI | https://doi.org/10.1051/epjn/2018016 | |
| Published online | 29 June 2018 | |
https://doi.org/10.1051/epjn/2018016
Regular Article
A comparison of uncertainty propagation techniques using NDaST: full, half or zero Monte Carlo?
OECD Nuclear Energy Agency,
Boulogne-Billancourt, France
* e-mail: ndast@oecd-nea.org
Received:
23
October
2017
Received in final form:
18
January
2018
Accepted:
4
May
2018
Published online: 29 June 2018
Uncertainty propagation to keff using a Total Monte Carlo sampling process is commonly used to solve the issues associated with non-linear dependencies and non-Gaussian nuclear parameter distributions. We suggest that in general, keff sensitivities to nuclear data perturbations are not problematic, and that they remain linear over a large range; the same cannot be said definitively for nuclear data parameters and their impact on final cross-sections and distributions. Instead of running hundreds or thousands of neutronics calculations, we therefore investigate the possibility to take those many cross-section file samples and perform ‘cheap’ sensitivity perturbation calculations. This is efficiently possible with the NEA Nuclear Data Sensitivity Tool (NDaST) and this process we name the half Monte Carlo method (HMM). We demonstrate that this is indeed possible with a test example of JEZEBEL (PMF001) drawn from the ICSBEP handbook, comparing keff directly calculated with SERPENT to those predicted with NDaST. Furthermore, we show that one may retain the normal NDaST benefits; a deeper analysis of the resultant effects in terms of reaction and energy breakdown, without the normal computational burden of Monte Carlo (results within minutes, rather than days). Finally, we assess the rationality of using either full or HMMs, by also using the covariance data to do simple linear 'sandwich formula' type propagation of uncertainty onto the selected benchmarks. This allows us to draw some broad conclusions about the relative merits of selecting a technique with either full, half or zero degree of Monte Carlo simulation
© J. Dyrda et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The TENDL evaluated nuclear data library [1], produced by the nuclear data modelling code TALYS is produced according to the Total Monte Carlo (TMC) and Unified Monte Carlo methodologies [2,3]. As a result, many randomly sampled realisations of the nuclear data are generated − in some cases these are made available to users. For the TENDL-2014 release, processed files in ACE format, compatible with the neutronics codes such as MCNP, SERPENT, etc., are also provided.1
This conveniently allows us to test the supposition, that the difference in keff with each of these random files, relative to the ‘zero-th’ (nominal) file can be predicted by Nuclear Data Sensitivity Tool (NDaST) [4], within acceptable accuracy. These Δkeff values, corresponding to the uncertainties from the nuclear data evaluation, can be calculated using the relative perturbations automatically generated by the tool and the multi-group sensitivity profile retrieved from the DICE database [5]. Essentially the set of sensitivity vectors is a case specific, first-order model surrogate that replaces the neutronics solver.
The JEZEBEL (PMF001) case from the ICSBEP handbook [6] was used as the test example, for the random 239Pu files taken from the evaluators. Identical, processed libraries were then used for an equal number of direct SERPENT calculations, and the resulting values, and their statistical distributions were compared. Seven of the principal neutron reactions were used to generate the perturbations for NDaST:
-
(n,elastic) − MT = 2
-
(n,inelastic) − levels MT = 51–80, 91 (continuum) and sum MT = 4, are included in TENDL-2014
-
(n,2n) − MT = 16
-
(n,f) − MT = 18
-
(n,γ) − MT = 102
-
(
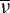 ) nubar − MT = 452
) nubar − MT = 452 -
(χ) chi − the prompt fission neutron spectra (PFNS) of secondary energies, tabulated for 97 different incoming neutron energies in TENDL-2014.
2 Uncertainty propagation methods
2.1 Total Monte Carlo (TMC)
The TMC methodology maintains to the best degree, the complete representation of all 'known uncertainties' in both the nuclear data evaluations and the resulting outcome of keff. Its results can be considered exact (to within statistical noise) for all high order responses and non-Gaussian parameter distributions. It also circumvents the need to analyse results using either evaluated multi-group covariances, or sensitivity co-efficients which must in turn be generated by a suitable code. These in turn must be well calculated (according to a group structure) and converged (when using a statistical estimator).
However, even advanced TMC processes [7,8] can be rather slow, i.e., requiring several hundreds or thousands of model solutions, and can obscure the detailed effects as a function of reaction and energy. This information can only be retained using post-regression analysis of the sampled parameters and the resulting correlation to keff. It is fair to conclude that the process is not generally accessible to most data users, firstly because of the paucity of random TMC evaluations at their disposal (TENDL being the main demonstrable option); and, because of the necessary computing power, without which the solution time could potentially run into several months or years per nuclide. Although TMC has been applied to core cycles studies [9], in general has been used to test that more simplified analyses are more-or-less accurate (and have concluded this is the case to within approximately 20% [10]).
2.2 Brute Force Monte Carlo (BFMC)
The methodology, on occasion known as Brute Force Monte Carlo (BFMC) [11] (not to be confused with Backward–Forward Monte Carlo), involves the user producing their own random library samples, based upon the covariance data representation within the evaluated file. It can therefore cope with non-linearity in the responses between cross-section changes and keff and does not require sensitivity data. It is therefore generally applicable to almost any code and data combination, since only the input information needs to be re-sampled and modified. However, it is still somewhat slow and can obscure details in terms of reactions and energy. In addition it necessitates a code capable of performing the sampling process in the manner required; several examples have been developed and demonstrated; NUDUNA (Areva), KIWI (LLNL), SANDY (SCK-CEN), SHARK-X (PSI), etc.
2.3 Linear propagation (sandwich formula) method
The TENDL-2014 239Pu evaluation file also contains reaction covariance data (C), representing the uncertainties and correlations between energies and reactions. These are processed using the NJOY2012 [12] code into BOXER format files for use within NDaST. In this way, in conjuction with the sensitivity profile (Sk), the uncertaintes can be linearly propagated to keff using the classical linear ‘Sandwich’ formula [13] method (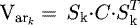 ). It requires no random libraries and is therefore convenient and quick to apply. Its other benefit is a more complete physical understanding of the resulting data, which is retained completely on a reaction and energy basis.
). It requires no random libraries and is therefore convenient and quick to apply. Its other benefit is a more complete physical understanding of the resulting data, which is retained completely on a reaction and energy basis.
In practice, this method is widely used within the nuclear data and application communities − even for determination of bias estimation in criticality safety limits. Thus the testing of this ‘Zero Monte Carlo’ approach against the Full or Half MC, and the adequacy of the processed covariance representations, is of relevance. In the most ideal situation, one would wish to retain the accuracy of the Full MC approach, but with the speed, efficiency and knowledge offered from the Zero MC classical method. The availability of NDaST for application of a half Monte Carlo method (HMM) may be one way by which this can be somewhat attained.
3 NDaST half Monte Carlo method (HMM) development
Since the recent introduction of the automated file upload feature in NDaST, along with the removal of the limitation to one single perturbation per reaction-nuclide, the HMM has become possible. The computation feature, leveraged from the JANIS tool, allows the quick loading of a series of perturbations, taking several numerators (the random files) and one denominator (the original file). Also developed in conjunction was the visualisation of these random sets, for each reaction-nuclide or combination, along with calculation of associated statistical measures (mean, standard deviation, skewness, kurtosis, etc).
One important note should be mentioned concerning χ; this is represented in general as a number (in the region ∼10–30) of probability distributions for several incoming neutron energies (E), as a function of outgoing energy (E′). In generation of the perturbations solely as a function of E′ therefore, one needs to weight the contributions from each of the incoming E. In this manner, compatibility with the sensitivity data units which are a function only of E′ is ensured. An appropriate weighting for the case(s) under investigation is required, and in this work the 299-group JEZEBEL fission spectrum calculated with KENO/ABBN-93, as taken from the DICE database was applied.
Numerical verification work of the HMM was performed, but is not reported here. For example, tests of energy interpolation functions were made to ensure best accuracy is maintained; also tested was the difference between forming the requested multi-group pertubation bins, before or after the division operation, the latter being the preferred and adopted choice.
3.1 The SANDY nuclear data sampling tool
The SANDY tool [14], developed at SCK-CEN, is a numerical tool for nuclear data uncertainty quantification. It is based on Monte Carlo sampling of cross-section parameters, according to best-estimate values and covariances. It works on ENDF-6 format files, taking one single file and sampling from a normally distributed multivariate pdf to produce N random samples still in ENDF-6 format [15]. It therefore offers flexibility, retaining the identical point-wise structure as the initial input file.
SANDY was used to sample 450 random realisations of the TENDL-2014 library, using the data from covariance files MF31, MF33 and MF35. Although it is capable also of using MF32 and MF34, these were not requested in the present case. When forming the union covariance matrix for MF33, large negative eigenvalues were noted, resulting in a non-positive definite matrix. This was solved simply by deleting, and ignoring, the cross-reaction correlations. Furthermore, the χ covariance distributions were observed to not comply with the ‘zero-sum’ rule. Therefore in each of the output files, re-normalisation of the PFNS distribution to unity was performed. Both of the above limitations are considered to be problematic artefacts of this particular nuclear data evaluation.
These SANDY sampled files were also passed both through NDaST and used in direct calculation of PMF001 using the SERPENT code [16]. Since the samples are formed from the covariances, this will be referred to as the 'backwards' HMM. This is as opposed to the samples produced from TALYS using input modelling parameter uncertainties in a 'forwards' sense.
4 Results and analysis
The results panel of the NDaST software is shown in Figure 1, where each random file is shown as a table row, and each reaction as a column. The value within the cell is the total Δkeff for that given combination; highlighting one or a number of cells shows the energy level detail as a series in the graph immediately below.
In Figure 2, the results of the Δkeff for each of the 988 random TENDL-2014 files are show, for both the direct method, using SERPENT as the Monte Carlo neutronics solver, and with the ‘forwards’ HMM method via NDaST. The bin widths are 200 pcm and vary from approximately −2000 pcm to +2500 pcm. The average difference between the two sets of values is only 13 pcm − on the same order as the statistical uncertainty in the Monte Carlo simulations. However, the offset is slightly greater on the ‘tails’, i.e., for the largest Δkeff values, with a maximum difference of 161 pcm. This is potentially a demonstration of a higher order dependency, where the linear sensitivity coefficients do not sufficiently well predict the perturbation effect.
The statistical distribution of the two sets of results (as calculated within MS Excel) are given in Table 1. The additional information available from NDaST, is the reaction-specific statistics, as shown in Figure 3. This can assist the user in better understanding the underlying processes, for instance the reasons for which a non-Gaussian distribution on keff is obtained; in the present case, fission cross-section and Chi both have a slightly negative mean and skewness to the distribution appears to have its main contribution from inelastic scatter.
 |
Fig. 1 NDaST output panel of Δkeff for PFNS for each random file as a function of energy. |
 |
Fig. 2 Comparison of Δkeff for both NDaST-HMM and direct calculation with SERPENT. |
Comparison of Δkeff distribution statistics for TENDL-2014 random files.
 |
Fig. 3 Comparison of Δkeff for NDaST-HMM by reaction, with distribution statistics. |
4.1 Comparison with TALYS HMM
Tables 2 and 3 show the comparison of results between the NDaST ‘forwards’ HMM and the sandwich method. Specific values are highlighted (in bold in Tab. 3) to show where the reaction totals are inconstent, i.e., for inelastic, fission, nubar and Chi. One can see therefore that the HMM gives insight into why the totals of 808 and 929 pcm differ (Tab. 1). However, it is difficult, based on the limited knowledge of how the random files were generated with TALYS as to the reasons for this. These could be allotted to reasons such as methods of constraint, evaluator choice, software/processing effects or the limited ability of covariances to capture high order/non-Gaussian responses.
The greatest inconsistency may be noted for the results in Chi-values of 93 and 470 pcm for HMM and sandwich method respectively. This value alone may therefore account for the differences in the summed totals. As a secondary check, an energy-wise covariance matrix was reconstructed from the perturbations calculated by NDaST as part of the HMM. This was subsequently used with the sensitivities to propagate to keff, in a secondary application of the sandwich method. The result was an identical 93 pcm, as the one calculated by the forwards HMM, however the difference in the relative standard deviation between this reconstructed covariance, and the original processed by NJOY is clearly evident in Figure 4.
Sandwich formula uncertainty propagation results.
Forwards HMM (TALYS) uncertainty propagation results.
 |
Fig. 4 Relative standard deviation of 239Pu PFNS in original TENDL-2014 evaluation and reconstructed from random samples. |
4.2 Comparison with SANDY HMM
The results in Table 4 show the difference between the SANDY generated random files − the 'backwards' HMM and the sandwich method. In this instance, one would expect a much better agreement, since SANDY uses the same file-contained covariances to re-generate its samples. This is generally the case, apart from the two cases highlighed (purple) − inelastic scatter and Chi. The inconsistency for the inelastic is most likely explained in how SANDY uses the covariance data associated with each of the several partial scattering levels, as opposed to the combined cross-section (MT4). It appears that in this case at least, the two approaches are not equivalent. These and the missing off-diagonal contributions result in a much lower total uncertainty of 652 pcm being obtained.
As before, the greatest difference is apparent for Chi − the 87 pcm uncertainty obtained is much closer to the ‘forwards’ HMM value from the TALYS random files. In this instance, because of the identical origin of the covariance data, we can almost certainly attribute the difference to the re-normalisation applied by SANDY. It does this to each of the random files when the integrated Chi probability distribution does not sum to unity. NJOY is understood to also apply some correction to covariances which do not conform to the zero-sum rule; documentation states that for the condition in equations (1) and (2) is applied. However this work seems to indicate some discrepancy between the two approaches or a processing/software mistake. Confirmation of the magnitude of the re-normalised variances was again found by reconstruction as above, this is shown as a third series in Figure 4. The effect is driven by the particularly high uncertainty above 2 Mev, coupled with JEZEBEL's sensitivity in this region (10% of fissions occur above 4 MeV and contribute 30% of the absolute χ sensitivity total) − this is also apparent in the energy-wise series shown in Figure 1.
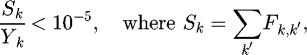 (1)
(1)
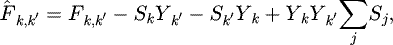 (2)
(2)
One final consideration made, was as to which of the incoming energy (E) covariance tables is used by NJOY for processing by its ERRORR module. This is controlled in the input by stating the mean energy of fission (Ef mean parameter), which if not specified defaults to 2 MeV. NJOY selects only the covariance whose energy-span includes the Ef mean value. To investigate, we processed BOXER data at eight additional energies, from thermal to fast spectra as shown in Table 5. Also shown are the propagated errors in keff obtained from using each of them. The range of the relative standard deviations associated with each of these is apparent in Figure 5. To obtain the most representative value for the case, one should apply a weighted sum of each of the values in Table 5, according to the case fission spectrum. It is clear however, that although this would have an effect, it cannot explain the larger discrepancies obtained by the 'forwards' and 'backwards' HMMs compared to the sandwich method.
Backwards HMM (SANDY) uncertainty propagation results.
PFNS keff uncertainties from different Ef mean values, default Ef mean = 2 MeV.
 |
Fig. 5 Relative standard deviation of 239Pu PFNS in TENDL-2014 for different NJOY Ef mean input values. |
5 Conclusions and further work
This work has described the development of a HMM in the NDaST tool maintained by the NEA. It makes use of the existing JANIS computations function, automating it for use of an alternative uncertainty propagation method. This method is many times faster than the full TMC methodology, but retains most of its rigour and gives a deeper insight for analysts into the reaction/energy effects with no additional computational burden. It was tested just for the PMF001 case (JEZEBEL sphere) in both a ‘forwards’ and ‘backwards’ sense and compared to the classical liner sandwich formula method, noting several instances of disagreement. However, there was generally very little difference between the Δkeff values generated by the HMM and with full Monte Carlo via SERPENT. Thus the method seems applicable, for all but extreme perturbations, giving rise to several thousand pcm difference.
Particular care was shown to be necessary for the handling of the inelastic scattering cross-section and PFNS (Chi) covariances, where specific choices in processing can lead to dramatic differences in the end results. The application of re-normalisation to non-zero-sum MF35 within NJOY warrants further investigation, as the results do not seem to exhibit those expected/intended. It would also be insightful for the analysis described here to be repeated for further integral experiment cases. In particular, more demanding cases could be identified where the zero-th file gives a different keff value than the average of the random files, i.e., strong skewness. Using other nuclear data evaluations would also show any particular problem or amplified effect obtained from either the TENDL-2014 library or the very fast spectrum associated with this case. Extension to parameters beyond keff such as benchmark spectral indices would also be of interest, particularly with respect to the demonstrated susceptibility to changes in the PFNS.
Finally, the wider availability of a means to generate randomly sampled libraries would be of great benefit. As discussed, the TALYS tool is not the most accessible to users of nuclear data. However, the ability at least to do 'backwards' sampling and pass these to NDaST for HMM (alike to a BFMC method) would replace the need for covariance processing and any of the pitfalls involved. It is the intention in the near future, to make the SANDY tool used here freely available, possibly via the NEA Databank Computer Program Service. Close pairing of this to NDaST would enhance greatly the NEA services in nuclear data processing and application.
References
- A.J. Koning, D. Rochman, Modern nuclear data evaluation with the TALYS code system, Nucl. Data Sheets 113, 2841 (2012) [CrossRef] [Google Scholar]
- D. Rochman, A.J. Koning, Living without covariance files, Workshop on Neutron Cross Section Covariances, Port Jefferson, NY, USA, 2008 [Google Scholar]
- R. Capote, D.L. Smith, An investigation of the performance of the unified Monte Carlo method of neutron cross section data evaluation, Nucl. Data Sheets, 109, 2768 (2008) [CrossRef] [Google Scholar]
- I. Hill, J. Dyrda, The half Monte Carlo method: combining total Monte Carlo with nuclear data sensitivity profiles, Trans. Am. Nucl. Soc. 116, 712 (2017) [Google Scholar]
- I. Hill, J. Gulliford, N. Soppera, M. Bossant, DICE 2013: New Capabilities and Data, Proc. PHYSOR , October 2014 (2014) [Google Scholar]
- International handbook of evaluated criticality safety benchmark experiments, September 2016 Edition. OECD/NEA Nuclear Science Committee, NEA/NSC/DOC(95)03 [Google Scholar]
- D. Rochman, W. Zwermann, S.C. van der Marck, A.J. Koning, H. Sjöstrand, P. Helgesson, B. Krzykacz-Hausmann, Efficient use of Monte Carlo: uncertainty propagation, Nucl. Sci. Eng. 177, 337 (2014) [CrossRef] [Google Scholar]
- P. Helgesson, H. Sjöstrand, A.J. Koning, J. Rydén, D. Rochman, E. Alhassan, S. Pomp, Combining total Monte Carlo and unified Monte Carlo: Bayesian nuclear data uncertainty quantification from auto-generated experimental covariances, Prog. Nucl. Energy 96, 76 (2017) [CrossRef] [Google Scholar]
- O. Leray, H. Ferroukhi, M. Hursin, A. Vasiliev, D. Rochman, Methodology for core analyses with nuclear data uncertainty quantification and application to swiss PWR operated cycles, Ann. Nucl. Energy 110, 547 (2017) [CrossRef] [Google Scholar]
- D. Rochman, A.J. Koning, S.C. van der Marck, A. Hogenbirk, C.M. Sciolla, Nuclear data uncertainty propagation: perturbation vs. Monte Carlo, Ann. Nucl. Energy 38, 942 (2011) [Google Scholar]
- M.E. Rising, M.C. White, P. Talou, A.K. Prinja, Unified Monte Carlo: Evaluation, Uncertainty Quantification and Propagation of the Prompt Fission Neutron Spectrum (EDP Sciences, France, 2013) [Google Scholar]
- R.E. MacFarlane, The NJOY Nuclear Data Processing System Version 2012, LA-UR-12-27079 Rev (2012) [Google Scholar]
- D.G. Cacuci, in Sensitivity and Uncertainty Analysis Theory (Chapman & Hall/CRC, 2003), Vol. I [Google Scholar]
- L. Fiorito, M. Griseri, A. Stankovskiy, Nuclear Data Uncertainty Propagation in Reactor Studies Using the SANDY Monte Carlo Sampling Code, in M&C 2017, Jeju, Korea, April 16–20, 2017 [Google Scholar]
- M. Herman, A. Trkov, ENDF-6 Formats Manual Data Formats and Procedures for the Evaluated Nuclear Data File ENDF/B-VI and ENDF/B-VII, BNL-90365-2009 (2009) [Google Scholar]
- J. Leppanen, PSG2/Serpent-A Continuous-Energy Monte Carlo Reactor Physics Bum up Calculation Code, VTT Technical Research Centre of Finland (2010): http://montecarlo.vtt.fi (current as of May 8, 2013) [Google Scholar]
Cite this article as: James Dyrda, Ian Hill, Luca Fiorito, Oscar Cabellos, Nicolas Soppera, A comparison of uncertainty propagation techniques using NDaST: full, half or zero Monte Carlo? EPJ Nuclear Sci. Technol. 4, 14 (2018)
All Tables
All Figures
 |
Fig. 1 NDaST output panel of Δkeff for PFNS for each random file as a function of energy. |
| In the text | |
 |
Fig. 2 Comparison of Δkeff for both NDaST-HMM and direct calculation with SERPENT. |
| In the text | |
 |
Fig. 3 Comparison of Δkeff for NDaST-HMM by reaction, with distribution statistics. |
| In the text | |
 |
Fig. 4 Relative standard deviation of 239Pu PFNS in original TENDL-2014 evaluation and reconstructed from random samples. |
| In the text | |
 |
Fig. 5 Relative standard deviation of 239Pu PFNS in TENDL-2014 for different NJOY Ef mean input values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


