| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
|
|
|---|---|---|
| Article Number | 21 | |
| Number of page(s) | 9 | |
| Section | Experimental Uncertainties | |
| DOI | https://doi.org/10.1051/epjn/2018026 | |
| Published online | 14 November 2018 | |
https://doi.org/10.1051/epjn/2018026
Regular Article
Template for estimating uncertainties of measured neutron-induced fission cross-sections
1
Los Alamos National Laboratory,
Los Alamos,
NM
87545, USA
2
Argonne National Laboratory,
Coronado,
CA
92118, USA (retired)
3
NAPC-Nuclear Data Section, International Atomic Energy Agency,
Vienna
1400, Austria
* e-mail: dneudecker@lanl.gov
Received:
31
October
2017
Received in final form:
29
January
2018
Accepted:
14
May
2018
Published online: 14 November 2018
A template for estimating uncertainties (unc.) of measured neutron-induced fission, (n,f), cross-sections (cs) is presented. This preliminary template not only lists all expected unc. sources but also supplies ranges of unc., estimates for correlations between unc. of the same and different experiments which can be used if the information is nonexistent. If this template is applied systematically when estimating experimental covariances for an evaluation, it may help in pinpointing missing unc. for individual datasets, identifying unreasonably low unc., and estimating correlations between different experimental datasets. Thus, a detailed unc. estimate – usually, a time-intensive procedure – can be undertaken more consistently and efficiently. As an example, it is shown that unc. and correlations of 239Pu(n,f) by Merla et al. [Proceedings of the Conference on Nuclear Data for Science and Technology 1991 Jülich (Springer-Verlag, Berlin, 1992) pp. 510–513], which are questionably low in the GMA database underlying the neutron cs standards evaluations, are distinctly larger at 14.7 MeV and more strongly correlated if this template is used for reestimating the associated covariances.
© D. Neudecker et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
We present preliminary work toward a template of uncertainties (unc.) typically encountered in neutron-induced fission, (n,f), cross-section (cs) measurements. A rough estimate of the range of these unc., their associated correlations for the same and between different experiments are provided which may help to estimate detailed unc. for an evaluation, if this information is missing. It occasionally happens that an important unc. source is missing in EXFOR [1,2] or the literature for a dataset, while correlations between different unc. are only rarely reported, and even less frequently correlations between unc. of different experiments are documented.
This template was designed to help experimentalists to provide the information necessary for nuclear data evaluations and evaluators in estimating detailed covariances of measured (n,f) cs systematically and efficiently. By using the template and comparing it to unc. provided for a specific dataset, one can easily identify missing unc. and questionably low unc. and fill in missing information and estimate covariances between experimental datasets in a consistent manner.
One example why such a template is needed, is the recent evaluations of neutron cs standards and references [3]. Portions of these evaluations, the 235,238U(n,f) and 239Pu(n,f) cs among them, are obtained by a generalized least squares analysis of the GMA database [4]. This database contains experimental data and covariances reestimated over several decades by expert judgment of experienced evaluators and experimentalists. The resulting nuclear data are considered to be among the most precisely and accurately known in the nuclear data libraries, and many other reactions are measured as ratios to these data. Nevertheless, it was questioned whether the evaluated unc. are too low given that they are about a factor 2–3 lower than can be achieved in any particular fission chamber measurement, and data measured with fission chambers were mostly used for (n,f) cs data in the GMA evaluation procedures. Therefore, an analysis of unknown systematic unc. [5] was included using a full overall correlation in the evaluation process based on the spread of data. This procedure led to a minimum evaluated unc. of 1.2% for (n,f) cs. This overall unc. provides an approximate estimate of (a) unrecognized unc. across many datasets due to using the same measurement method (i.e., fission chambers), (b) missing unc. sources for individual datasets, and (c) underestimated or missing correlations between unc. of different measurements. The template proposed here can help in addressing the issues (b) and (c), while (a) can be addressed by new types of precision measurements that shed light on the unc. sources of conventional measurements (e.g., the NIFFTE TPC measurement [6]). This work can also contribute along the same lines for CIELO evaluations which supply covariances and as input for the WPEC SG44 project.
Section 2 discusses the data types for which this template was established and why differentiation between different data types is needed. The actual template is discussed in Section 3, while an example highlighting the advantages of applying the template is shown in Section 4 by means of the code ARIADNE [7]. The paper concludes with a summary and outlook in Section 5.
2 Types of (n,f) cs measurement
We distinguish between six different (n,f) cs measurement types, as different unc. sources and ranges of unc. apply dependent on the measurement type. For instance, the detector efficiency unc. needs to be quantified for an absolute measurement, while it might reduce or cancel in clean ratio measurements, or needs to be supplied for both detectors in a ratio measurement using two different detectors.
In general, one can distinguish between “absolute” and “shape” measurements. For absolute measurements, the target mass needs to be determined to fix the normalization of the data. In shape measurements, the target mass is not quantified and the normalization floats during the standard evaluation procedure. One also can distinguish between measurements of the (n,f) cs itself or the (n,f) cs as a ratio to another reaction cs. Details on these measurement types are provided below.
2.1 Absolute data
In an absolute measurement, the (n,f) cs is determined directly. The normalization of the data is defined by quantifying experimentally the number of atoms in the sample, the uniformity of the sample and the uniformity and magnitude of the incident neutron flux. Attenuation effects are assumed to be, in general, larger than in clean ratio measurements and about the size of indirect ratio measurements. Multiple scattering effects are expected to be larger for absolute measurements than for clean ratio measurements if the same collimators and very similar detectors are used.
2.2 Shape data
Shape measurements provide directly (n,f) cs without a set normalization. Thus, the number of atoms in the sample is not quantified, nor is the magnitude of the neutron flux specified, and no associated unc. need to be considered. The same assumptions for attenuation and multiple scattering effects apply as for absolute data.
2.3 Clean ratio absolute data
A clean ratio absolute measurement provides (n,f) cs data measured as a ratio to a reference measurement using one fission detector. Given that both isotopes are measured with one detector, usually a fission chamber, both isotopes are expected to be fissile. The detector efficiency might cancel for carefully designed clean ratio measurements, and thus no associated unc. are considered. The detector efficiency will not fully cancel if, for instance, the samples are of different size. Also, in a back-to-back configuration of 235U and 238U samples, these isotopes react differently to background neutrons, and there also may be kinematic effect differences at higher energies E leading to nonnegligible correction factors and thus unc. for the detector efficiency. Both isotopes see the same neutron flux and, therefore, it cancels out or only very small corrections apply. Hence, no neutron flux unc. apply to the total unc. budget. Attenuation affects a clean ratio measurement less than an absolute measurement if collimators and detectors are of similar size and materials, because only those neutrons which are lost between the sample of the monitor reaction and the isotope in questions need to be considered as neutrons lost before affect both isotopes the same way and thus cancel. Multiple scattering effects are expected to be less problematic as they affect both fissile isotopes similarly, but not in completely the same way. While multiple scattering effects do not cancel completely, the residual effect is smaller than in absolute measurements if similar fission detectors and the same collimators, etc., are used. Contrary to absolute measurements, the number of atoms in the samples need to be quantified for both isotopes rather than only for one, leading to an increased normalization unc.
2.4 Clean ratio shape data
Clean ratio shape measurements provide (n,f) cs measured as ratios to a reference isotope using one fission detector for both isotopes without a set normalization. Consequently, the number of atoms in either isotope need not be determined, and associated unc. are not included in the sources of unc. Otherwise, the same assumptions apply as for clean ratio absolute data.
2.5 Indirect ratio absolute data
Indirect ratio absolute measurements provide (n,f) cs measured as a ratio to a reference isotope. Unlike clean ratio absolute measurements, the reference isotope is measured with a different detector than the (n,f) cs. Using two detectors, allows to measure the fission cs as a ratio to a nonfission reaction. This possibility is especially of interest at low energies, where sub-threshold fission reactions show resonances and this nonsmooth behavior makes these reactions less ideal for ratio measurement. For example, a 239Pu(n,f) cs measured as a ratio to 10B(n, α) is an indirect ratio measurement. Since different detectors are used for both measurements, the detector efficiency and associated unc. have to be provided for both measurements. However, both isotopes see the same neutron flux; therefore, it cancels out or only a small correction has to be made, and the associated unc. need not be considered. Attenuation is expected to affect indirect ratio data more than clean ratio data if the same collimators and fission detectors are used, as the neutron beam has to travel through more material to induce the monitor reaction. Multiple scattering effects are expected to be reduced less than in clean ratio measurements, as they affect the fissile isotopes distinctly differently than a nonfissile monitor isotope due to their different cs. While multiple scattering effects cancel to some extent, additional material present in the neutron beam produces more scattering compared to absolute measurements using similar fission detectors and the same collimators, etc. The multiple scattering effect still can be reduced compared to absolute measurements, depending on the specifics of the material in the measurement area. As for clean ratio absolute data, the number of atoms in the sample need to be quantified for both isotopes.
2.6 Indirect ratio shape data
Indirect ratio shape data provide (n,f) cs measured as a ratio to a reference reaction. The total unc. budget of indirect ratio shape data does not include unc. due to the number of atoms in either isotope because shape data do not have set normalizations. Otherwise, the same assumptions apply as for clean ratio absolute data.
3 Template of uncertainties
Below, we describe unc. sources typically encountered in (n,f) cs measurements, a reasonable range of these unc. relative to the measured quantity, and an estimate of the correlations between unc. of the same and different experiments. This information is summarized in Tables 1 and 2. The unc. sources typically encountered were established by extracting unc. sources found for all 239Pu(n,f) cs in the GMA database. The ranges of unc. and correlations are preliminary, established based on discussions with experimentalists and information found in EXFOR and GMA entries. A broad literature study is currently missing.
This template can be used to compare to unc. provided for a measurement, pin-point missing unc., or questionably low unc. for a detailed unc. estimate. It provides a rough estimate for missing information for both unc. and correlation information. It is a “poor man's” choice and should not be used instead of reasonable information provided in EXFOR or the literature for a measurement. However, it is still better than assuming the missing unc. is 0 which would effectively give the experimental data more weight in the evaluation than is physically justified.
A list of unc. sources typically encountered in (n,f) fission cs measurements is provided together with a range of unc., their correlations, and comments on possible cross-correlations between unc. of different experimental datasets as a rough estimate if no information is provided for a specific experiment.
An estimated range of unc. for specific unc. sources is listed for absolute, absolute clean ratio and absolute indirect ratio data. The unc. for shape data of the same kind are analogous except for δN which is 0%.
3.1 Sample mass unc.δN
The sample mass has to be determined for all absolute type measurements. Closely related to the sample mass is its chemical and physical composition since that affects the atom number determination. Unc. in the corrections of impurities in the samples are described below. If only part of the sample is illuminated by the neutron-beam, the sample mass has to be determined along with the size of the neutron beam. It also needs to be known if the neutron-beam, the sample(s) or both are nonuniform to derive the correct (n,f) cs from measured counts. If multiple samples are used, the sample mass and nonuniformity of each sample need to be quantified.
The unc. in determining the sample mass is a dominant unc. source for any type of absolute measurements. It is hard to achieve an unc. better than 1% for fission deposits, especially if it estimates possible biases in the sample mass, the nonuniformity of the sample and beam. If just the unc. in the mass of the sample are accounted for, 0.5% is a realistic rough estimate. In any absolute ratio measurement, unc. for both samples need to be accounted for, and this leads to an increased total δN compared to absolute measurements.
As one or a set of samples is usually used for all energies of one measurement, an error in the sample mass would affect all cs equally. Thus, a biased sample mass leads to an error in the normalization of the measured observable. Hence, the correlation matrix associated with δN is usually fully correlated for all E of one measurement. Cross-correlations of 1 between δN of different experiments would arise if the same samples (not necessarily the same detectors) are used and their mass and uniformity are determined with the same techniques.
3.2 Counting statistics unc. δc
The finite counting time leads to a limited number of measured counts and thus to δc. It depends on the counting time, the cs itself and the binning size chosen for the data. The larger the incident energy bins, the smaller δc.
Unc. as low as 0.2% are physically possible, but δc = 0% is impossible. If δc is missing, a reasonable estimate could be achieved by using δc agreeing on average with those of other measurements of the same observable in a similar energy range and binning. In ratio measurements, δc is often given combined, for counts of both samples, although it might be technically possible to provide δc for both samples separately. It is, however, important that the experimentalist documents whether δc on the ratio data includes unc. for both samples or just the isotope in question. Otherwise, an additional δc for the monitor sample needs to be added arbitrarily if δc is suspiciously low.
δc is random in nature for each E, and, therefore, has 0 correlation between different E for the same and between different experiments.
3.3 Attenuation unc. δβ
Attenuation means the loss of incident neutrons in the structural material or gas before the isotope fissions. The absolute size of the effect depends on the material between the neutron beam and the fission target. It is expected to be smallest for clean ratio measurements as only the neutrons lost between the two targets have to be accounted for, while in absolute/shape measurements all neutrons lost on the way to the target have to be accounted for. The correction is larger for indirect than clean ratio measurements, if the material and size of fission detector and collimators are very similar due to the amount of material in the beam. Usually, the correction for attenuation (often combined with a correction for multiple scattering) is calculated with a program such as MCNP-6 [8]. These calculations and δβ depend on the physics models, nuclear data used, and the goodness of the input model of the code.
For clean ratio measurements, δβ is expected to be given combined for the actinide in question and the monitor isotope, as attenuation between both foils is assessed in a combined manner. For indirect ratio measurements, δβ could be given separately. For indirect ratio and absolute measurements, δβ could be approximately 2% up to 200 keV, decreases linearly to 0.2% at 20 MeV, and stays constant above. For clean ratio measurements, the shape of the unc. dependence on E is expected to be the same but an order magnitude less in size.
δβ is expected to be highly correlated for energies close together for the same experiment because nuclear data used in the codes to simulate attenuation effects are often strongly correlated for neighboring energy bins. For energies far apart, the correlation is assumed to decrease because different reaction types might contribute to the simulation. A possible, speculative, correlation shape would be a Gaussian-shaped functional form,
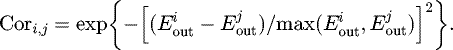 (1)
(1)
Nonzero correlations between different experiments arise when the same code or underlying nuclear data are used. Equation (1) can be used as an assumption for the cross-correlations.
3.4 Detector efficiency unc. δϵ
Detector efficiencies less than unity account for the loss of fission fragment counts and are usually calculated with programs such as TRIM [9]. The efficiency is constant up to about 10 MeV, and follows a functional form of E defined by kinematics calculations for E> 10 MeV.
δϵ applies to absolute, shape, and indirect ratio data. Even in clean ratio measurements, the detector efficiency, and hence δϵ, might not fully cancel as noted above, especially at high E due to kinematic effects affecting the two isotopes differently, leading to δϵ≈ 0.3%. In absolute and shape measurements, δϵ≈ 1%–2% is reasonable based on expert judgment. In an indirect ratio measurement, δϵ needs to be given for the fission detector and for the detector measuring the monitor reaction. As mentioned above, δϵ =1.0%–2.0% is realistic for the fission chamber, while 1.0% could be assumed for an α counter.
We expect the δϵ to be fully correlated for E≤10 MeV, and above a weakening of correlations following equation (1) if no correlation information is provided. If several unc. sources defined here are lumped together in a “detector efficiency unc.” (e.g., what is termed δα, the fission fragment angular distribution correction unc., and δϵ here), the correlations might no longer be fully correlated. Therefore, one should always be careful what the author includes in a specific unc. component. When estimating correlations between experiments, one needs to distinguish clearly whether the measurements involved are absolute, clean ratio, or indirect ratio measurements. If the same or very similar underlying assumptions were used to determine the detector efficiency values of two different absolute or shape experiments using both fission chambers, an overall correlation of around 0.5–0.75 between the experiments can be assumed. The same underlying assumptions are, for instance, usage of the same code with the same nuclear data, or usage of the same kinematics calculations. In the case of indirect ratio measurements relative to, e.g., the 10B(n,α) or 6Li(n,α) monitor reactions, one needs to assess correlations between δϵ of both detectors. We assume that the correlations between these two types of detectors are zero due to different underlying assumptions while the correlations between δϵ of the same detector type are described above.
3.5 Fission fragment angular distribution correction unc. δα
There are two different contributions which could lead to an anisotropic fission fragment angular distribution: (1) The kinematic boost of the fission fragments above 10 MeV which is fairly well understood and can be corrected. It might be considered in the detector efficiency, and, then, the associated unc. is part of δϵ. This effect is expected to be the same for two different fissile targets and is expected to cancel for clean ratio measurements using two targets of the same thickness with both deposits facing in the same direction. The effect is present in absolute or shape measurements, and remains for indirect ratio measurements if the monitor isotope is nonfissile. (2) The inherent anisotropy of fission fragment emission depends on the isotopes measured. Therefore, it does not cancel in any type of measurement. The effect might be smaller for clean ratio measurements than absolute/shape or indirect ratio measurements if the anisotropy of fission fragment emission is similar for the actinide in question and the monitor isotope. The fission fragment distribution is assumed to be isotropic up to 50–500 keV depending on the isotope. This effect is not well-studied, and it is a possible unc. source affecting many measurements. It can lead to significant δα at high energies if the detector efficiency is small.
For highly efficient fission chambers, δα is expected to be small and 0% is possible for all measurement types. For E< 100 keV, fission fragments are expected to be emitted isotropically and the kinematic boost is negligible, hence, δα can be assumed to be 0% even for less efficient chambers. For indirect ratio, absolute, and shape measurements using a non high-efficient fission chamber, however, the anisotropy of fission fragments can have an impact for E&z.gap; 5 MeV leading to δα of up to a few %. In clean ratio measurements, δα≤ 0.1% at all E if the fission fragment distribution is similar for both isotopes.
The unc. of the kinematic boost are highly correlated as the same functional form is used. A Gaussian correlation shape as described in equation (1) could be used as an approximation with all correlation coefficient above 0.75. A similar assumption could be made for the unc. related to correcting for the inherent anisotropy of the fission fragments as these are corrected by strongly correlated data. An overall correlation factor of 0.75–1.0 is recommended for estimating the correlations between δα of different experiments as in general the same calculations or data are used.
3.6 Background determination unc. δb
Usually, the background is measured and fitted to a functional form which is then used to correct the measured count rate for the background. The background and δb depend strongly on the measurement environment, energy E and the facility producing the neutron-beam. Therefore, it is difficult to estimate δb applicable to many experiments of different facilities. Background affects all type of measurements because of different threshold of reactions in ratio measurements.
Usually, δb is one of the dominant unc. sources. It is technically possible to achieve δb as low as 0.2%–0.3%, while several tens of % can be realistic if the measurement was not carefully designed to minimize background. δb = 0.5% is a realistic lower limit to be assigned if it is missing. For example, if Monte Carlo techniques are used to simulate the neutron environment, the multiple scattering correction unc., δm, is lumped together with δb. If neither of those unc. are given for an absolute, shape, or indirect ratio measurement, a lower-limit estimate would be between 0.5% and 1.0%. For clean ratio measurements, the lower limit estimate would be 0.5%, as multiple scattering should partially cancel.
If a functional form with few parameters is used, a strong correlation is expected between background unc. of neighboring points. If the functional form is explicitly given, it can be used to derive correlations from it, otherwise the Gaussian shape of equation (1) with a correlation above 0.5 could be used. If two measurements were undertaken at the same facility but the background correction methods differ, or at different facilities with the same method, we assume an overall correlation of 0.5, 0.75 if they were undertaken at the same facility and used the same background correction, otherwise 0.
3.7 Energy unc. δE
Time-of-flight (TOF) length unc., δEl, and time resolution unc., δEt, apply to TOF measurements, while unc. relative to the energy E are provided for mono-energetic measurements (e.g., associated particle measurements).
δE = 1%–5% relative to energy are possible for mono-energetic measurements. If δEl or δEt are missing for fission chambers, 3 mm or 1–3 ns, respectively, would be a realistic estimate. The TOF-path length needs to be well-known to convert these unc. into those relative to the (n,f) cs. δEl and δEt apply to absolute, shape and clean ratio measurements, as only one detector – a fission detector – is used for the measurement, while they need to be provided for both detectors for indirect ratio measurements. One can also estimate δEt to be 1–3 ns for detectors measuring the 10B(n,α) or 6Li(n,α) reaction, if missing, where 3 ns is the upper bound for any of the detectors mentioned above. This estimate is applicable to older measurements where the electronics were slower and electronic drift had to be corrected, while δEt of 0.5–1 ns can be reached in today's 10B(n,α) or 6Li(n,α) measurements. (or even more near the threshold)
The average correlation of energy unc. in mono-energetic measurements is estimated to be 0.5 in energy space due to a mixture of random and systematic components in determining the E. For the associated particle method, the energy of the associated particle is measured and used to derive E given the known energy of the neutron-producing particle leading to the mixture of random and systematic components. Low correlations of 0–0.25 are assumed to appear only between δE of different experiments if the same technique was used. The correlations between different δEl and δEt arise from the conversion of δEl and δEt in mm and ns to an unc. relative to the (n,f) cs. Correlations between δEt of different experiments only apply if both measurements are TOF measurements. We estimate the correlation between δEt of different experiments to be high (0.8) if the same detector is used for both measurements because usually different electronics are used, and that can lead to random shifts in one or another direction, dependent on the neutron flux. If the same detector type (not the same detector) is used at different facilities, this overall correlation drops down to 0.5. No correlations between δEl of different experiments are assumed.
3.8 Neutron flux determination unc. δϕ
The neutron flux has to be determined only for absolute measurements. Only its shape is quantified for shape measurements, and it cancels or reduces to a small correction factor in ratio measurements resulting in a δϕ of 0%. The neutron flux depends strongly on the facility where it was produced, but methods to quantify it can be the same, resulting in correlations between δϕ of different experiments. In some cases, the neutron flux is measured relative to (n,p) scattering. The unc. related to (n,p) scattering are very low, but it is difficult to use and, hence, the method and the experimental set-up can introduce additional unc. In the associated particle method, the neutron flux is determined by measuring the random coincidences of charged particles with the neutron-producing reaction while fission events are recorded. E is then determined by the kinematics of the charged particles.
The neutron flux is very hard to determine better than 1% so this can be used as a lower limit. It is thus a major unc. source for absolute measurements. δϕ is sometimes coined “random coincidences” in measurement using the associated particle method. For measurements as ratios to (n,p), unc. for this measurement and nuclear data unc. should be taken into account.
Usually, the shape of the neutron flux is known very well, but how it is derived results in a not fully correlated δϕ. If nuclear data were used to determine the neutron flux, a covariance matrix is usually provided for these data, and it can be used to estimate covariances for δϕ. When estimating the correlations between δϕ of the same measurement using the associated particle method, the correlations are weakened because of the statistical unc. contribution of the random coincidence measurement. One would expect nonzero correlations to arise between absolute measurements employing the same technique to determine the neutron flux and zero otherwise. We estimate a correlation of 0.5 between δϕ of two measurements employing either the associated particle method or measuring relative to (n,p) scattering. This estimate is based on the fact that usually similar techniques, the same nuclear data and/or detectors are used to measure the flux, while random counting statistics unc. reduce the overall correlation factor.
3.9 Multiple scattering correction unc. δm
As multiple scattering, we understand neutrons loosing energy before causing fission because of scattering in collimators and the detector(s). This effect results in an assumed (n,f) cs assigned to an erroneously higher E than really is the case. While the size of this effect depends on the measurement environment, collimators and detectors used, it is expected to be largest in absolute and shape measurements, smaller for indirect ratio measurements and smallest for clean ratio measurements, as detailed above. Usually, multiple scattering corrections are calculated with codes such as MCNP-6 [8] and measurements are made to verify these simulations.
The correction itself is usually small, but the unc. δm on this correction can be large and 1% is not unlikely, while 0% is unreasonable. Often, δm is reported combined with δb. If neither of those unc. are given for absolute, shape or indirect ratio measurements, a conservative estimate would be between 0.5% and 1.0%. For clean ratio measurements, a combined lower-limit estimate, δb and δm, of 0.5% is reasonable, although reaching unc. as low as 0.2%–0.3% is also technically possible. Nonzero correlations between δm for all measurement types of the same and different experiments arise because the same or similar codes, nuclear data, or physics assumptions were used for the corrections. In lieu of a precalculated correlation matrix, we estimate the correlations of δm for the same experiment to follow the shape in equation (1), mirroring the behavior of nuclear data covariances, while an overall correlation of 0.5 is estimated roughly for correlations between experiments if auxiliary measurements are employed to validate the simulated correction.
3.10 Unc. due to correction of impurities in the sample δζ
If an, e.g., 235,238U or 239Pu, (n,f) cs measurement is undertaken above threshold with a sample of purity ≤ 99%, the correction of impurities is usually small. However, it can be large for sub-threshold reactions and less pure samples. The level of the contamination and the (n,f) cs of the contaminating isotopes need to be known to correct for the impurities. The former effect leads usually to larger unc. than the latter. If δζ is missing, reasonable estimates can be achieved by comparing to measurements of the same isotope, with similar contaminants in a similar energy range.
The unc. of the absolute value of the contamination in the sample is fully correlated, as one sample is employed for the whole measurement. The unc. on the (n,f) cs of the contamination has a nuclear data covariance matrix which is usually not fully correlated. The covariance matrix related to δζ can be estimated by combining the covariances described above. If that is not possible because only a joint δζ is given, equation (1) can be used such that no correlation coefficient is smaller than 0.9. We estimate an overall correlation factor of 0.5–0.75 between δζ of different experiments using the same isotopes because usually the same starting material and manufacturing process are employed to generate the sample as well as the same methods determining their impurities and the same nuclear data are used for the impurity correction. The same starting material and manufacturing process would also lead to a similar amount of contamination in the samples. If the same samples are used for two measurements as well as the same methods for the contamination correction, the correlation between δζ is 1.
3.11 Nuclear data unc. δσND
Nuclear data might be needed to convert ratio data to (n,f) cs data. Usually, covariances are supplied for the nuclear data which can be used for estimating correlations between δσND for the same experiment or between different experiments if the same nuclear data are used. It is very important that the experimentalist specifies exactly which nuclear data are used by citing the version/number as covariances of δσND can be estimated easily (if the experimentalists provide partial rather than total unc.) and nuclear data can be updated with improved evaluated data.
3.12 Dead time correction unc. δd
During the dead time of a detector (or in older measurements the computer processing dead time), no counts are detected and corrections need to be applied for all types of measurements. Even for clean ratio measurements, the detector halves can have a different dead time. For instance, α-particles produced in a 239Pu(n,f) measurement generate much higher count rates than when measuring 235U(n,f) leading to different dead times. The effect of dead time can amount to several % but it can be corrected accurately, so a δd = 0.1% is reasonable. Pile-up of signals causes a dead time that is harder to correct becoming an issue for very high rate experiments.
Usually the shape of the dead time correction is very well known from statistical laws leading to the assumption that δd is fully correlated for the same experiment. As it is measured separately for each experiment, we assume zero correlation between δd of different experiments.
4 Example applying the template
4.1 Reestimation of GMA dataset DS611
As an example, to show how the template can aid in estimating detailed unc., the unc. of the dataset DS611 in GMA by Merla et al. [10–12] were reestimated. This 239Pu(n,f) dataset was chosen as it has the lowest total unc. (1%) compared with all other absolute 239Pu(n,f) GMA data. A 1% total unc. is questionable given that it is hard to measure the neutron flux and the background to better than 1.0% and 0.5%, respectively. In the associated EXFOR entry, only partial unc. for the energy and δm are provided along with a questionably low total unc. It is unclear where the partial unc. listed in GMA and tabulated in Table 3 are coming from. However, it is noteworthy that the total unc. in EXFOR and GMA are comparable.
The partial unc. were reestimated based on Table 1 in reference [12] providing typical unc. ranges for the associated particle method and in comparison to the template presented here. For instance, for δN, δϵ and δb the largest unc. of the range provided in reference [12] was chosen based on the information in the template. Comparing the unc. sources provided in the template with those in GMA highlighted that δα and δζ were missing. δζ could be added easily based on that provided for measurements at different E of the same group with the same sample [10], while δα was estimated based on Table 1. The resulting total unc. in Figure 1 calculated with ARIADNE are distinctly larger than those in GMA and EXFOR. They are more reasonable considering the unc. in this template but also given that the second smallest total unc. for absolute 239Pu(n,f) in GMA amounts to 2%.
In Figure 1, reestimated unc. are shown also for GMA datasets DS615–617 which were measured by the same collaboration. The total reestimated unc. of DS615 and DS617 are very similar to the total unc. estimated in GMA given the detailed unc. analysis provided in reference [10]. The reestimated unc. of dataset DS616 is slightly smaller than the GMA total unc. because the statistical unc. provided in EXFOR (δc =1.52%) is used for the reestimate rather than the 2.52% provided in Table 2 of reference [10] which was used in GMA. δc =2.52% was assumed to be erroneous as the total unc. in the same table was given with 2.39%, i.e., lower than δc.
The unc. of the data by Merla et al. – “DS611” in GMA – provided in EXFOR, GMA and reestimated here are listed for each unc. source of the template. All unc. are given in % with δE given relative to E and all others relative to the cs.
 |
Fig. 1 The data of Merla et al. [10–12] are shown as given in the file GMA.res (dated Feb. 3, 2017) of GMA and in EXFOR along with a reestimated total unc. The file GMA.res gives all experimental data with total uncertainties after data reduction to a common energy grid. Therefore, GMA E and cs values differ slightly from their EXFOR values. |
4.2 Reestimation of correlations between GMA datasets DS611, DS615–617
The template was also used to estimate correlations between the datasets DS611, DS615–617 in GMA. They are treated separately in GMA, but are given within two EXFOR entries, and were actually measured by the same group of scientists with the same equipment. Hence, strong correlations should apply because of correlations between δN, δb, δϵ, δα, δb, δE, δφ, δm and δζ of these data. The total correlations reestimated using correlation information in the template are distinctly larger than in GMA (Fig. 2). These larger correlations are justified given that all data were measured within the same experiment using the same equipment. The template aided here in highlighting missing correlations.
 |
Fig. 2 The total correlations of Merla et al. data in GMA (right-hand side) are compared to the reestimated ones. |
5 Summary and outlook
Considering unc. estimated in a detailed way versus a simplified manner can impact evaluated data, benchmark simulations and their unc. distinctly, as was for instance shown for the 239Pu prompt fission neutron spectrum and the Jezebel assembly in reference [13]. Estimating detailed unc. is a time-intensive procedure and unc. sources and correlations could be easily overlooked leading to underestimated unc. As an example, the evaluated 235,238U and 239Pu(n,f) unc. provided by the standards community were just increased by introducing an unknown systematic unc. source, given the suspicion that they are unreasonably small due to missing unc. and correlations.
Therefore, a template was created listing typical unc. sources, their expected ranges, and correlations between the same and different experiments for (n,f) cs. This template should aid in identifying missing unc. sources and filling in the missing information on relative unc. and correlations in a systematic and efficient manner. It can also aid experimentalists in providing unc. information for their measurements. As example, it was shown how the template aided in reestimating unc. of 239Pu(n,f) cs included in the standards evaluation database. The resulting unc. and correlations are no longer unreasonably low.
The template is preliminary, as presented at the CW2017 workshop, and it is mostly based on expert judgment gained from discussing the issues with experimentalists. In the near future, a broad literature research will be undertaken to provide additional and more refined information. This updated template will then be applied to estimate fission cs unc. in GMA, and it will be studied if adding missing, but known, unc. and correlations might lead to more reasonable evaluated unc. comparable to those estimated now by introducing an unknown unc. source.
Author contribution statement
D. Neudecker established the template in Tables 2 and 3 based on work of B. Hejnal and discussions with F. Tovesson, M.C. White and D.L. Smith. B. Hejnal and D. Neudecker derived algorithms to be used for the uncertainty estimate in Section 4, D. Neudecker extended ARIADNE [7] to include these algorithms and undertook the uncertainty estimate in Section 4. B. Hejnal extracted information from all 239Pu(n,f) cs measurements in GMA which was the basis for establishing the types of (n,f) cs measurements, uncertainty sources and ranges of uncertainties for these different sources. This information was verified and extended in discussions with F. Tovesson, M.C. White and D.L. Smith. F. Tovesson, M.C. White and D.L. Smith provided key input about (n,f) cs measurements in general and which uncertainty sources should be considered for (n,f) cs measurement, what reasonable sizes of these uncertainties are and assumptions for correlations if this information is not provided for a particular measurement. D. Vaughan provided guidance from a general uncertainty quantification point of view, especially on the estimation algorithm for the covariances. R. Capote supplied key information from the neutron data standards effort and provided input on the needs of the neutron data standard evaluation effort.
Acknowledgments
This work was carried out partly under the auspices of the NNSA of the U.S. Department of Energy at LANL under Contract No. DE-AC52-06NA25396.
References
- Experimental Nuclear Reaction Data Library (EXFOR), IAEA Nuclear Data Section. See https://www-nds.iaea.org/exfor (accessed on 10/16/2017) [Google Scholar]
- N. Otuka et al., Nucl. Data Sheets 120, 272 (2014) [CrossRef] [Google Scholar]
- A.D. Carlson et al., Nucl. Data Sheets 148, 143 (2018) [Google Scholar]
- W. Poenitz, Argonne National Laboratory Report ANL/NDM-139, 1997 [Google Scholar]
- S.A. Badikov et al., IAEA Report INDC(NDS)-438, 2003, pp. 117–129 [Google Scholar]
- M. Heffner et al., Nucl. Inst. Methods Phys. Res. A 759, 50 (2014) [Google Scholar]
- D. Neudecker et al., ARIADNE – a program estimating covariances in detail for neutron experiments, EPJ Nuclear Sci. Technol. 4, 34 (2018) [CrossRef] [EDP Sciences] [Google Scholar]
- C.J. Werner et al., Los Alamos National Laboratory Report LA-UR-13-22934, 2017 [Google Scholar]
- J.P. Biersack et al., Nucl. Inst. Methods 174, 257 (1980) [Google Scholar]
- K. Merla et al., in Proceedings of the Conference on Nuclear Data for Science and Technology, 1991, Jülich (Springer-Verlag, Berlin, 1992), pp. 510–513 [Google Scholar]
- I.D. Alkhazov et al., in Proceedings of the Conference on Nuclear Data for Science and Technology, 1988, MITO (JAERI, Mito 1988), pp. 145–148. See http://wwwndc.jaea.go.jp/nd1988/index.html [Google Scholar]
- R. Arlt et al., in Proceedings of the Conference on Nuclear Cross Sections for Technology, 1979, Knoxville (National Bureau of Standards Special Publication, 1980), pp. 990–994 [Google Scholar]
- D. Neudecker et al., Nucl. Data Sheets 131, 289 (2016) [CrossRef] [EDP Sciences] [Google Scholar]
Cite this article as: Denise Neudecker, Brooke Hejnal, Fredrik Tovesson, Morgan C. White, Donald L. Smith, Diane Vaughan, R. Capote, Template for estimating uncertainties of measured neutron-induced fission cross-sections, EPJ Nuclear Sci. Technol. 4, 21 (2018)
All Tables
A list of unc. sources typically encountered in (n,f) fission cs measurements is provided together with a range of unc., their correlations, and comments on possible cross-correlations between unc. of different experimental datasets as a rough estimate if no information is provided for a specific experiment.
An estimated range of unc. for specific unc. sources is listed for absolute, absolute clean ratio and absolute indirect ratio data. The unc. for shape data of the same kind are analogous except for δN which is 0%.
The unc. of the data by Merla et al. – “DS611” in GMA – provided in EXFOR, GMA and reestimated here are listed for each unc. source of the template. All unc. are given in % with δE given relative to E and all others relative to the cs.
All Figures
 |
Fig. 1 The data of Merla et al. [10–12] are shown as given in the file GMA.res (dated Feb. 3, 2017) of GMA and in EXFOR along with a reestimated total unc. The file GMA.res gives all experimental data with total uncertainties after data reduction to a common energy grid. Therefore, GMA E and cs values differ slightly from their EXFOR values. |
| In the text | |
 |
Fig. 2 The total correlations of Merla et al. data in GMA (right-hand side) are compared to the reestimated ones. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


