EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 4 (2018) EPJ Nuclear Sci. Technol., 4 (2018) 22 Full HTML
Issue
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
Article Number 22
Number of page(s) 4
Section Experimental Uncertainties
DOI https://doi.org/10.1051/epjn/2018017
Published online 14 November 2018

© Y. Danon, published by EDP Sciences, 2018

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Accurate nuclear data is required for accurate calculation of nuclear reactors, criticality safety, shielding, and other applications. Nuclear Physics models can calculate some quantities such as average cross sections but to obtain the required accuracy for the above applications experimental data must be used to bound the models. For example; resonance region evaluations are based on shape fitting of measured resonance data, and thus accurate and precise experiments are required to reduce uncertainties. Current nuclear data evaluated libraries are well established and are a topic of strong collaboration between different evaluation groups across the world (for example the CIELO [1] project and the WPEC collaboration [2]). Past experiments are documented in the EXFOR data base [3], which is extensively used by evaluators. When new experiments are considered the reason should be well justified including target accuracy. The new information must be of sufficient quality that will help increase the accuracy and reduce the uncertainty of existing evaluations. The high priority list maintained by subgroup C of WPEC provides a list of materials for which a justification for new measurements and their target accuracy was provided by nuclear data users.

2 Innovative experiments

In this paper we try to distinguish “conventional” from “innovative” experiments of neutron induced cross section measurements. The term conventional refers to established methods; for example, measurements of neutron transmission and capture documented in reference [4]. Such measurements use similar detectors and common methods worldwide; therefore, they are established methods, which were shown to provide both accurate and precise data. However, in some cases innovative methods can be used to reduce the uncertainty of the measured data and increase accuracy relative to the conventional methods. Such experiments are referred to as innovative. This paper cannot cover all possible innovations; instead, a few specific examples will be given. These examples describe a modification of a conventional experiment that results in uncertainty reduction and aim to increase accuracy.

2.1 Background reduction

In a typical TOF neutron transmission experiment a neutron detector is placed in a well collimated neutron beam and the sample to be measured is cycled in and out of the beam. The transmission can be calculated as the ratio of the background corrected sample-in to sample-out (open) count rate for each TOF bin. Usually neutron beam monitors are used to normalize the open and sample count rates to the same beam intensity. Equation (1) describes the process for TOF bin i, it also gives the relation of the total cross section to the transmission. 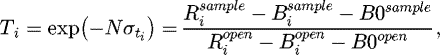(1) where N is the number density of the sample, 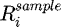and 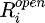are the sample and open monitor normalized count rates, and 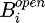are sample and open time dependent gamma background shapes, and B0sample and B0Open are the sample and open time independent backgrounds. The time dependent background has multiple sources such as the neutron production target, the collimation system, and backscatter from the surroundings; it varies between different facilities. The filtered beam method can be used in TOF measurements by placing a thick filter such as iron in the neutron beam [5]. The resonance potential interference creates a quasi-monoenergetic source. In the case of iron, the useful energy range is between 24 and 1000 keV. The thick iron filter (≈30 cm) removes most beam associated (time dependent) neutron and gamma background. Figure 1 is an example of open beam counts measured with a 30 cm iron filter. The background is calculated in the wing of the peaks, and an excellent signal to background ratio between 200 and 400 keV can be demonstrated [5].

The iron filter method was also used for background reduction in TOF capture measurements of 181Ta [6] in the unresolved resonance range. In the case of 181Ta, the level density is sufficiently high that each filter peak compass many resonances and thus provides a good statistical average. Figure 2 is an example of the filtered beam measured capture cross section compared with an unfiltered measurement and evaluations. Figure 2 shows that the method works well for the stronger filter beam peaks and results in lower uncertainties for those.

thumbnail Fig. 1

Example of counts obtained in an iron filtered beam experiment. The bottom plot shows peaks in the useful energy range and the top plot shows the signal and background for one of the peaks used in a transmission measurement of Be. For full experimental details see reference [5].
thumbnail Fig. 2

Neutron capture cross section of 181Ta measured with an iron filtered beam compared with an unfiltered measurement and different evaluations [6].

2.2 Transmission normalization

In Section 2.1 monitor normalization in transmission measurements was discussed. A monitor detector is selected to be a very stable detector such as a fission chamber that provides sufficient count rate. The uncertainty on the normalization depends on the correlation between the monitor detector and the in-beam detector. It is desirable that the ratio of the two detector will be one for all short runs during an experiment. A typical behavior is shown in Figure 3. The fluctuations are larger than the statistical uncertainty with an average of 1.000 ± 0.013. These fluctuations will translate to a normalization uncertainty.

In the frame work of CIELO there was a concern about three percent uncertainty in previous high resolution transmission measurements of 16O in the energy range of 0.5–6 MeV. To resolve this issue a new water transmission measurement was conducted at RPI [7]. Water was selected because it contains 16O and also H for which the scattering cross section is a standard and the capture cross section is small. To check the normalization the strong minimum in the 16O total cross section at 2.34 MeV was utilized. In this resonance nearly all the total cross section of water is from the hydrogen. The data in Figure 4 resulted in a ratio 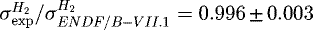at 2.34 MeV. Thus the normalization uncertainty was verified to be much lower than the three percent required for this experiment.

thumbnail Fig. 3

Beam monitor to in-beam detectors ratio as a function of the run number. Each run represents about 17 min of data acquisition time. The observed fluctuations are larger than the statistical uncertainty.
thumbnail Fig. 4

Measured transmission for two thicknesses of water samples are shown. Also plotted are calculations using the ENDF/B-VII.1 [8] cross sections for H2O and for only H in the sample. The agreement of the H2 transmission serves as verification of the normalization.

3 Neutron scattering

Double differential neutron scattering experiments require an array of detectors that surrounds the scattering sample [9] or movable detectors or swinger beam [10]. Unlike a transmission experiment, the detector efficiency as a function of energy needs to be known with a high degree of accuracy. Measurement of inelastic double differential cross section is even more complicated and for that reason often the angle integrated cross section is measured using the inelastic gammas emitted from the sample (for example [11]). Because of the complexity such experiments result in higher uncertainty compared to transmission and capture measurements. To provide high accuracy experimental data an experiment that measures all the neutron emissions from the sample was developed at RPI [12]. This is a quasi-differential scattering measurement that can be compared to simulations of the experiments using different cross section evaluations. It can be used with thick and thin scattering samples, and the data are normalized relative to a reference with well known cross section (carbon). Such normalization eliminated the need to measure the absolute detection efficiency and only the shape as a function of neutron energy is needed for the simulations. This method also requires information regarding the shape of the neutron source energy spectrum. More information on use of this method in evaluation can be found in references [13,14].

4 Simultaneous neutron capture and fission measurements

Measurements of the capture cross section using the conventional TOF method, where the capture cascade gammas are measured, is more difficult in the case of a fissionable nuclide because of prompt fission gammas that have to be discriminated against. The usual way to achieve that is by using a fission chamber that contains the sample. The gammas emitted from the sample are counted in anticoincidence with the fission chamber signal. The fission chamber places a limitation on the mass that can be used and a multiplate fission chamber was often employed [15]. Even in this case the mass is limited to a few hundreds of milligrams. The limit on the mass results in a low counting rate, which, together with the need to know the fission detection efficiency, contributes to the uncertainty.

A way to get around this problem is to use a highly efficient nearly 4π gamma detector that will measure both capture and fission gammas and use some method to separate the different contributions [16].

An implementation of such a method can use the cascade multiplicity and total gamma energy deposition. For example, the 235U capture gamma cascade total energy is given by the binding energy, Eb = 6.55 MeV. Thus events that result in a higher energy deposition (Edep > Eb) can only come from fission, which has a higher gamma energy release. In addition, the observed capture gamma multiplicity is ≈4, while for fission it is ≈8. This difference provides another way of separating capture from fission events. The difficulty with this method is separation of capture from fission for events with Edep < Eb where the capture and fission total energy deposition is of the same order. An assumption that must be made is that the gamma spectrum and multiplicity are not dependent on the neutron incident energy. For 235U this is a good assumption for incident neutrons below 100 keV.

Recently, two measurements using such methods were published [17,18]. In reference [17] a fission chamber was used to measure the fraction of fission gammas in the total gammas measured. This fraction was later used to correct the measurement. In reference [18] the fission yield was first obtained from events with Edep > Eb. The fission yield was then subtracted from the total yield measured with events Edep < Eb by normalization to two known capture yields (resonance integrals or the thermal capture cross section). The grouped results from reference [18] are shown in Figure 5 and were used to help resolve the difference between the evaluations of 235U in the energy range from 500 to 3000 eV. The agreement between the evaluation and the measure fission yield is very good, but there are differences in the capture yield that were tabulated in reference [18].

thumbnail Fig. 5

Fission (top) and capture (bottom) yield measurement of 235U compared with the evaluated data libraries [18].

5 Conclusions

This paper was written to encourage when possible using methods that provide an improvement over conventional cross section measurements in order to increase the accuracy of nuclear data. The experiments described are all TOF experiments that are common in nuclear data measurements. Examples were given that demonstrate reduction in uncertainty due to background and normalization. An example was given of a quasi-differential scattering experiment used to test the performance of different evaluations and also provide sufficient information to improve evaluations. An example was also provided for simultaneous measurements of fission and capture cross section that can help increase the accuracy of capture measurements. These examples demonstrate that for some cases using an innovative or different methodology can be useful and provide information to improve nuclear data evaluations.

References

  1. M. Chadwick, E. Dupont, E. Bauge, A. Blokhin, O. Bouland, D. Brown, R. Capote, A. Carlson, Y. Danon, C.D.S. Jean et al., Nucl. Data Sheets 118, 1 (2014) [CrossRef] [Google Scholar]
  2. E. Dupont, M. Chadwick, Y. Danon, C.D.S. Jean, M. Dunn, U. Fischer, R. Forrest, T. Fukahori, Z. Ge, H. Harada et al., Nucl. Data Sheets 120, 264 (2014) [CrossRef] [Google Scholar]
  3. N. Otuka, E. Dupont, V. Semkova, B. Pritychenko, A. Blokhin, M. Aikawa, S. Babykina, M. Bossant, G. Chen, S. Dunaeva et al., Nucl. Data Sheets 120, 272 (2014) [CrossRef] [Google Scholar]
  4. P. Schillebeeckx, B. Becker, Y. Danon, K. Guber, H. Harada, J. Heyse, A. Junghans, S. Kopecky, C. Massimi, M. Moxon et al., Nucl. Data Sheets 113, 3054 (2012) [CrossRef] [Google Scholar]
  5. Y. Danon, R. Block, M. Rapp, F. Saglime, G. Leinweber, D. Barry, N. Drindak, J. Hoole, Nucl. Sci. Eng. 161, 321 (2009) [CrossRef] [Google Scholar]
  6. B.J. McDermott, E. Blain, A. Daskalakis, N. Thompson, A. Youmans, H.J. Choun, W. Steinberger, Y. Danon, D.P. Barry, R.C. Block et al., Phys. Rev. C 96, 014607 (2017) [CrossRef] [Google Scholar]
  7. Y. Danon, E. Blain, A. Daskalakis, B. McDermott, N. Thompson, A. Youmans, R.C. Block, D. Barry, B. Epping, G. Leinweber et al., AccApp 15, (Washington, DC, 2015) pp. 345–350 [Google Scholar]
  8. M. Chadwick, M. Herman, P. Obloinsky, M. Dunn, Y. Danon, A. Kahler, D. Smith, B. Pritychenko, G. Arbanas, R. Arcilla et al., Nucl. Data Sheets 112, 2887 (2011) [CrossRef] [Google Scholar]
  9. A. Smith, P. Guenther, R. Larsen, C. Nelson, P. Walker, J. Whalen, Nucl. Instr. Meth. 50, 277 (1967) [CrossRef] [Google Scholar]
  10. R. Devito, S.M. Austin, U. Berg, W. Sterrenburg, L. Young, Nucl. Instr. Meth. Phys. Res. 215, 423 (1983) [CrossRef] [Google Scholar]
  11. R.B. Day, Phys. Rev. 102, 767 (1956) [CrossRef] [Google Scholar]
  12. F. Saglime, Y. Danon, R. Block, M. Rapp, R. Bahran, G. Leinweber, D. Barry, N. Drindak, Nucl. Instr. Meth. Phys. Res. A 620, 401 (2010) [Google Scholar]
  13. A. Daskalakis, R. Bahran, E. Blain, B. McDermott, S. Piela, Y. Danon, D. Barry, G. Leinweber, R. Block, M. Rapp et al., Ann. Nucl. Energy 73, 455 (2014) [CrossRef] [Google Scholar]
  14. R. Capote, A. Trkov, M. Sin, M. Herman, A. Daskalakis, Y. Danon, Nucl. Data Sheets 118, 26 (2014) [CrossRef] [Google Scholar]
  15. J. Balibrea, E. Mendoza, D. Cano-Ott, C. Guerrero, E. Berthoumieux, S. Altstadt, J. Andrzejewski, L. Audouin, M. Barbagallo, V. Becares et al., Nucl. Data Sheets 119, 10 (2014) [Google Scholar]
  16. G. Muradyan, Y.V. Adamchuk, Y.G. Shchepkin, M. Voskanyan, Nucl. Sci. Eng. 90, 60 (1985) [CrossRef] [Google Scholar]
  17. M. Jandel, T.A. Bredeweg, E.M. Bond, M.B. Chadwick, A. Couture, J.M. O'Donnell, M. Fowler, R.C. Haight, T. Kawano, R. Reifarth et al., Phys. Rev. Lett. 109, 202506 (2012) [CrossRef] [PubMed] [Google Scholar]
  18. Y. Danon, D. Williams, R. Bahran, E. Blain, B. McDermott, D. Barry, G. Leinweber, R. Block, M. Rapp, Nucl. Sci. Eng. 187, 291 (2017) [CrossRef] [Google Scholar]

Cite this article as: Yaron Danon, Innovative experiments for reduction of nuclear data uncertainty, EPJ Nuclear Sci. Technol. 4, 22 (2018)

All Figures

thumbnail Fig. 1

Example of counts obtained in an iron filtered beam experiment. The bottom plot shows peaks in the useful energy range and the top plot shows the signal and background for one of the peaks used in a transmission measurement of Be. For full experimental details see reference [5].
In the text
thumbnail Fig. 2

Neutron capture cross section of 181Ta measured with an iron filtered beam compared with an unfiltered measurement and different evaluations [6].
In the text
thumbnail Fig. 3

Beam monitor to in-beam detectors ratio as a function of the run number. Each run represents about 17 min of data acquisition time. The observed fluctuations are larger than the statistical uncertainty.
In the text
thumbnail Fig. 4

Measured transmission for two thicknesses of water samples are shown. Also plotted are calculations using the ENDF/B-VII.1 [8] cross sections for H2O and for only H in the sample. The agreement of the H2 transmission serves as verification of the normalization.
In the text
thumbnail Fig. 5

Fission (top) and capture (bottom) yield measurement of 235U compared with the evaluated data libraries [18].
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.