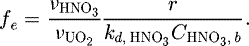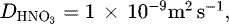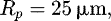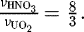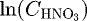| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
|
|
|---|---|---|
| Article Number | 2 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/epjn/2017026 | |
| Published online | 06 March 2018 | |
https://doi.org/10.1051/epjn/2017026
Regular Article
A method for phenomenological and chemical kinetics study of autocatalytic reactive dissolution by optical microscopy. The case of uranium dioxide dissolution in nitric acid media
1
CEA, Nuclear Energy Division, Research Department on Mining and Fuel Recycling Processes, Research Service for Dissolution and Separation Processes, Laboratory of Dissolution Studies,
30207
Bagnols-sur-Cèze, France
2
Laboratoire Réactions et Génie des Procédés, UMR CNRS 7274, University of Lorraine,
54001
Nancy, France
* e-mail: alastair.magnaldo@cea.fr
Received:
14
December
2016
Received in final form:
4
October
2017
Accepted:
10
October
2017
Published online: 6 March 2018
Dissolution is a milestone of the head-end of hydrometallurgical processes, as the stabilization rates of the chemical elements determine the process performance and hold-up. This study aims at better understanding the chemical and physico-chemical phenomena of uranium dioxide dissolution reactions in nitric acid media in the Purex process, which separates the reusable materials and the final wastes of the spent nuclear fuels. It has been documented that the attack of sintering-manufactured uranium dioxide solids occurs through preferential attack sites, which leads to the development of cracks in the solids. Optical microscopy observations show that in some cases, the development of these cracks leads to the solid cleavage. It is shown here that the dissolution of the detached fragments is much slower than the process of the complete cleavage of the solid, and occurs with no disturbing phenomena, like gas bubbling. This fact has motivated the measurement of dissolution kinetics using optical microscopy and image processing. By further discriminating between external resistance and chemical reaction, the “true” chemical kinetics of the reaction have been measured, and the highly autocatalytic nature of the reaction confirmed. Based on these results, the constants of the chemical reactions kinetic laws have also been evaluated.
Key words: Autocatalysis / dissolution / image processing / kinetics / microscopy / nitric acid / uranium dioxide
© P. Marc et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Dissolution is a key phenomenon encountered in various processes, for example for drug delivery, quality control in pharmacology [1] or in the food-processing industry [2,3]. Dissolution also takes part in many chemical processes in the mining industry [4–7], batteries [8,9], fertilizer production [10], or the recycling industry [11]. Among these chemical processes, the Purex process is a hydrometallurgical process involving the dissolution of spent nuclear fuels in nitric acid in the head-end steps, before carrying out solvent extraction steps allowing the recovery of uranium and plutonium [12]. In an optimization approach of this dissolution step, its modeling has recently become a source of interest. Given that currently recycled spent nuclear fuels are made of about 95% of uranium dioxide [13], the modeling of the dissolution of this chemical specie in nitric acid media represents a step which cannot be overlooked.
An analysis of the state of knowledge of the dissolution reaction of uranium dioxide in nitric acid media [14] shows that despite the importance of this reaction in the hydrometallurgical reprocessing of spent nuclear fuels, its chemical and physico-chemical mechanisms remain poorly understood. The relationship between the fraction of dissolved solid, which can be linked more or less simply with the bulk concentration of the chemical elements composing it, and the chemical reaction kinetics requires the accurate knowledge of the surface of the dissolving solid and the reactivity of each element of this surface over time. As a result of the physico-chemical phenomena occurring during the dissolution of uranium dioxide macroscopic solids in nitric acid media, like the complex reactions and species produced in nitric acid, the chemical reaction kinetics are today impossible to relate to the evolution of the concentration of dissolved materials in the bulk.
However, a recent trend in dissolution mechanisms and kinetics study is the use of optical microscopy. This technic has already been used in several dissolution studies. Steiger et al. used it for general observation of the growth and dissolution of lithium mosses and needles in 1 mol l−1 LiPF6 [8] and during lithium electrodeposition on tungsten and copper substrates [9]. Boetker et al [15]. studied the concentration gradients and diffusion layer thickness around amlodipine besylate dissolving in water, as well as Østergaard et al. [16] for lidocaine dissolution in water and Delwaulle et al. [17,18] for copper and uranium dioxide dissolving in nitric acid. Mgaidi et al. [4] and Singh et al. [19] used it for monitoring the evolution of the morphology of sand and succinic acid crystals during dissolution. The temporal studies vary from the measurement of total dissolution time of sucrose crystals in melted sorbitol by Bhandari et al. [2] to more complex studies which used optical microscopy for measuring the dissolution rates of several solids, such as those from Marabi et al. [3] for the dissolution rates of pure sucrose spherical particles in water, ethylene glycol, and polyethylene glycol, Forny et al. [20] for those of milk powder particles in water, and Dorozhkin [10,21] for single crystals of the natural Khibin (Kola) fluorapatite. Prasad et al. [22] and Raghavan et al. [23,24] have even measured the dependency of dissolution rates of paracetamol and α lactose monohydrate crystals in water depending on the crystal faces considered.
More recently, Svanbäck et al. [25–27] have addressed papers summarizing the advantages of optical microscopy as a method for dissolution kinetics measurements over the macroscopic methods, and presenting interesting designs for the cells and methods for the monitoring of such reactions. Part of these advantages are the reduction of the amounts of reagents required, the simpler experimental preparation (no compound-specific method development, calibration or evaluation is required for image analysis), which reduced the time required for analysis and the inter-operator variability error sources, and the low cost of the optical microscopy equipment compared to other technics such as HPLC-MS or GC-MS. However, the application of the presented cells in the dissolution conditions used for uranium dioxide (i.e. warm and concentrated nitric acid, implying strong acidic and oxidizing conditions) has not been possible as such, and dissolution cells fitting these conditions have been developed and will be presented in this paper.
It will also be shown that, during the dissolution of a uranium dioxide pellet, fragments can detach from it. Even if these fragments dissolved in a much simpler way than the pellet itself, two issues make them remain unsuitable for macroscopic chemical reaction rates studies. The first one is that even at this scale, non-uniform attack occurs, as documented by Briggs [28,29], Shabbir and Robbins [30] and Zhao and Chen [31–33], and thus that the surface and associated reactivity remain practically impossible to know precisely over time. The second issue is that the measurement of dissolving elements released in solution would require the use of several fragments, and of a larger volume of dissolution solution, thus rising the question of the accumulation of dissolution products, and their autocatalytic effect.
On the other hand, these fragments offer a good opportunity to measure the dissolution rates in situ by using optical microscopy and image processing. The determination of the rate determining step during these measurements allows to discriminate diffusion controlled from chemically controlled dissolutions. The study of the rates corresponding to the chemical reaction has shown that, without doubt, it occurs through a strongly autocatalyzed mechanism. Optical microscopy has also allowed measuring specifically the chemical reaction rates for the non-catalyzed reaction, leading to the proposal of reactivity ratios between the non- and the autocatalyzed reactions.
2 Experimental section
2.1 Microscope
The microscope used for this study is a reversed optical microscope Zeiss .Z1m equipped with three lenses offering magnification ratios of 5, 20 and 40. The reverse position of the lenses is required by the production of nitrogen oxides bubbles during the attack of uranium dioxide by nitric acid: when these bubbles rise to the top of the liquid, they hide the solid and make any observation by the top impossible.
The microscope has been installed in a depressurized glove box, in order to confine radioactive materials (Fig. 1).
 |
Fig. 1 Microscopy installation in the glove box. |
2.2 Dissolution cells
A first continuous dissolution cell is presented in Figure 2. It is composed of a central well where the solid and the solution are introduced. It is closed bottom-side by a quartz pothole in order to ensure observation. The upper part can be closed by rings system, which can be changed depending on the kind of experiments. The dissolution volume is 15 ml. This central well is surrounded by a jacket in which water can flow to maintain a stationary temperature in the central well. A coil, guaranteeing an optional continuous feed of the well with dissolution solution, circulates in this jacket so as to heat the solution inflow at the working temperature. Another pipe crosses the jacket in a straight line, allowing outflow and also placing a temperature sensor in the well. This device is well adapted for dissolution of macroscopic solids, dissolution under continuous flow, or batch dissolution of microscopic solids requiring important liquid/solid ratios.
The solution feed is controlled by a KD Scientific Legato 270 Push/Pull Syringe Pump coupled with a Gemini 88 Valve Box for long time ranging experiments.
A second device is presented in Figure 3. It consists in a quartz disc at the center of which a well has been manufactured. Around the well, a groove receives an O-ring seal, and a quartz disk placed over the system closes it. This device is placed on a thermoelectric heating stage Linkam PE100 adapted for the microscope. The control of the temperature is realized by a Linkam T95 system controller. In order to insulate the system, a polydimethylsiloxane cover designed to fit the heating stage has been manufactured by moulding.
Temperature stabilizing is more difficult with this non-circulating device, due to the configuration of the thermoelectric system : the time require for stabilizing the temperature is long (several hours), and there are important differences between the temperature set and the effectively reached temperature once the system is stabilized.
 |
Fig. 2 Pictures of the continuous dissolution cell. |
 |
Fig. 3 Thermoelectric device for the observation of the dissolution of microscopic solids. |
2.3 Reagents
Uranium dioxide powder was provided by CEA Cadarache. The uranium dioxide purity of the powder is 99.6%, and detailed analysis of the powder is given in Table 4 in the Supporting information.
This powder is also used for the manufacturing of the uranium dioxide pellets. The pellets have been pressed at a pressure of 518 MPa before being sintered at 1100 °C during 4 h under Ar-H2 (4%) atmosphere. Resulting sintered pellets have an average diameter of 4.66 mm, height of 4 mm and mass of 0.5 g.
Nitric acid solutions have been prepared by dilution of 68% HNO3 provided by VWR (ref. 20422.297). Each diluted solution have been titrated three times by mean of a 848 Titrino Plus, fed with 1 mol l−1 sodium hydroxide Titrinorm provided by Prolabo (ref. 180.031627.60).
2.4 Dissolutions in solutions containing reaction products
The autocatalytic component of the dissolution reaction of uranium dioxide in nitric acid media has been widely documented in the literature [14]. The ratio of the volume of dissolution solution over dissolved amount of solid in the dissolution cells is an advantageous condition for studying this component under well known dissolution products concentrations and temperature conditions.
The solutions for the measurement of dissolution kinetics in presence of various amounts of reaction products have been prepared by pre-dissolving uranium dioxide powder in fresh nitric acid (Fig. 4). The dissolution is realized in a bottle containing a known volume of fresh nitric acid initially at room temperature, with a known mass of uranium dioxide powder introduced in the bottle, whose opening is immediately covered with a cork after the introduction of the powder, in order to limit the evacuation of gaseous reaction products. The bottle is not hermetically closed to avoid overpressure troubles during the reaction. Four solutions with a pre-dissolved amount of uranium dioxide of 0.1, 10, 50, and 100 g l−1 have been prepared in fresh 4.73 mol l−1 nitric acid.
The time required (about 10 min) for the transfer of the solution to the microscope glove box insures that potentially remaining undissolved uranium dioxide gets completely dissolved. The solution is then continuously pumped at a 5 ml h−1 flow rate into the dissolution cell, and the dissolution of the uranium dioxide fragments under the microscope starts. Even if this continuous flow contributes to guarantee the stability of the concentrations of the reagents and products in the cell at the values of the pre-dissolved uranium diocide solutions, it is primarily used, in the absence of a consolidated knowledge on the autocatalytic species and their stabilities, to counter as much as possible a potential degradation of the autocatalytic species.
 |
Fig. 4 Diagram of the experimental protocol for the study of the autocatalyzed reaction kinetics. |
2.5 Measurement of dissolution kinetics by optical microscopy observation and image processing
The methodologies used in previous dissolution kinetics measurement studies for calculating the dissolution rates from a set of images are usually not detailed [3,10,21]. These methods consist in measuring the distance between the profiles of one dissolving solid at different times. This distance corresponds to Δl on Figure 5, without stating if only one or several measurements are done along the profile.
A different method, based on the measurement of the projected area and the associated perimeter of a dissolving particle on each image, is developed here and detailed in the following paragraphs. The geometric evolution of the projected area of a uniformly dissolving solid is represented in Figure 5:
In the particular case of a weak dissolution of the particle, and in the absence of neo-formed phases at the solid/liquid interface, a mathematical link can be drawn between the variation of its projected area (A) between times t and 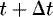 , the perimeter (P) of its projected area at t, and the progression of the dissolution front (
, the perimeter (P) of its projected area at t, and the progression of the dissolution front (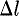 ), which corresponds to the apparent dissolution rate (r) over Δt, considered as constant over
), which corresponds to the apparent dissolution rate (r) over Δt, considered as constant over 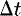 (Eq. (1)) :
(Eq. (1)) :
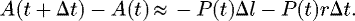 (1)
(1)
Thus, one of the advantages of this method is to focus on the measurement of the external perimeter of the solid, and to be able to make dissolution rates measurement without the issue of the internal porosity disturbance. equation (1) leads to the expression of the variation of the area at a time t (Eq. (2)) :
 (2)
(2)
Therefore, it is possible to extract the dissolution rate of a dissolving solid by measuring its area and perimeter on each image of a time sequence set of images. In practice, the integrated form of equation (2) (Eq. (3)) will be used on the sets of images, since this form allows smoothing the variations which can appear in the case of images with a poor quality, for example when the images are acquired under reflected light conditions.
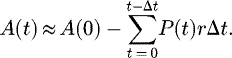 (3)
(3)
Considering the dissolution of the solid as uniform, and taking place under stationary conditions, it comes that the dissolution rate is constant over the time, and can be extracted from the sum sign, as well as the time interval Δt between two images, since this value is fixed by the experimenter, and thus is also constant over the acquisition. This leads to express the projected area of the particle at a time t as a linear function of the sum of the perimeters of the projected area from t = 0 to 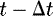 (Eq. (4)).
(Eq. (4)).
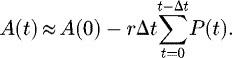 (4)
(4)
It is important to insist on the fact that these equations are practicable in the case of a uniform attack of the fragments. Nevertheless, it is not impossible that, even if no porosity development was detected at the scale of the grains we have been working with, microporosity development occurs at a smaller scale than the resolution of the microscope. It should be noted that in this case, if micro-porosity were created, it would also disappears at the same rate during dissolution: the dissolution would fatally appear non-uniform in the other case. Thus, the dissolution front moves globally uniformly at the resolution of the microscope.
In this case, the dissolution kinetics is given as a speed, in distance per time units. Assuming the density is known, the relationship between the reactive surface and the measured surface is linear, and equation (5) enables to convert these kinetics into more common units system for dissolution kinetics.
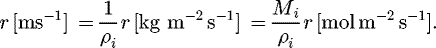 (5)
(5)
The measurement of area and perimeter used in this method raises the issue of the relevance of the dissolution kinetics measured in the case of a non-uniform attack of the solid. Once more, the problematic of the evolution of the rugosity and porosity of the surface is one of the main problem which has to be dealt with when measuring the chemical dissolution reaction kinetics, whatever the method applied [34–37], since there is no method for in-situ measurement of the surface evolution on such a short period of time.
A first fact to take into consideration is that in any case, porosity appears, but also disappears. This results in a stabilization of surface roughness after a given period of time. In the case of microscopic observations and image processing, two different cases must be considered depending on the scale they occurred at, and regarding the resolution of the images.
The first case applies when the surface roughness evolves at a smaller scale than the resolution of the microscope. In this case, the effect of the development of surface roughness on the measured area and perimeter of a given particle is null, or at least weak. What is more important is the case where the evolution of the surface roughness of the solid is detectable with the microscopic observations. In this case, the initial dissolution rate measured by this method will be greater than the average of the different reaction kinetics. Nevertheless, while the surface roughness will stabilize, the measured dissolution rates will get closer to the expected average of the dissolution rates.
Thus, concerning the method presented in this paper, one can draw the conclusions that the dissolution rates measured with this method are at least as good as those measured by classical macroscopic method, and in many cases even better since they only take under consideration the external surface, and not the complex and disrupting contribution of internal porosity.
 |
Fig. 5 Evolution of the projected area and associated perimeter of a uniformly dissolving particle. |
2.6 Image processing for the extraction of the area and perimeter of the particles
The analysis of the images is realized through a three-step process which consists of image binarisation, extraction of the area and perimeter of the particle, compilation of the data, and linear regression to calculate the dissolution rate.
The processing of a series of images is realized by the mean of a program developed in-house1 for the automation of this process.
2.6.1 Image binarisation
After turning the images from colored to 8-bits grayscale images, the luminosity of each pixel of the image varies from 0 (black) to 255 (white). The histogram representing the number of pixels composing the image as a function of their luminosity is a bimodal curve. One of the two peaks corresponds to the pixels of the background (black on Fig. 6), and the other to the pixels of the object (white on Fig. 6).
In order to measure the area and perimeter of a particle, it is first required to clearly separate the pixels of the image in two categories: object and background. This issue is widely documented in image treatment literature [38–43] and several methods have been proposed to define the threshold value.
The method selected defines the threshold as the luminosity for which the pixels population reaches a minimum between the two peaks. For this purpose the histogram is first smoothed by a moving average with a subset of nine values (Fig. 7).
This treatment results in a binary image, where pixels value is 0 if they belong to the background or 1 if they belong to the object. It can led pixels belonging to the solid to be categorized as background pixels, which would falsify the calculation of the solid area. This calculation relies on the counting of the pixels belonging to the solid, and thus requires to fill these holes before going further in the image treatment. Figure 6 presents the result of the complete treatment applied to a reflected light image.
 |
Fig. 6 Example of image thresholding and holes filling: original image (a), binarised image (b), and binarised image with holes filled (c). |
 |
Fig. 7 Example of threshold establishing. |
2.6.2 Extraction of the area and perimeter
The calculation of the area of the object on the segmented image consists in counting the number of pixels which belong to the object, and multiplying this number by the area of a pixel.
For the perimeter, it requires the determination of border pixels. It is assumed in the analysis of the images that if a pixel of the object has one of its neighboring pixels belonging to the background, then it belongs to the border. Once the border pixels have been identified, their contribution to the total perimeter is refined depending on their environment, as shown in Figure 8.
 |
Fig. 8 Possible configurations of the neighborhood of a pixel belonging to the perimeter of the object. |
2.6.3 Calculation of the dissolution rate and identification of the rate-determining step
The measured areas are plotted as a function of the sum of the perimeters, according to equation (4). A linear regression, given the time lapse between the images, gives the corresponding dissolution rate. An example of the result of this treatment is presented in Figure 9 for a set of images of a dissolving uranium dioxide fragment in 4.93 mol l−1 nitric acid at ∼343.15 K.
Once the dissolution rate has been measured, it is important to ascertain if this rate corresponds to the chemical reaction rate or to a diffusion rate.
For this purpose, the stoichiometric equation (9), identified in a former paper as the most likely taking place [14], has been retained for the balance of the reaction:
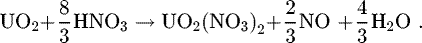 (6)
(6)
Evaluating the rate determining step can be achieved by evaluating the concentrations ratio at the surface of the solid to the bulk, by means of the external resistance ratio fe, also known as Mear's criterion (Eq. (6), where i stands for the reacting specie diffusing through the diffusion layer) [44–46].
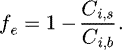 (7)
(7)
Considering stationary conditions in the diffusion layer, a mass balance gives:
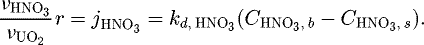 (8)
(8)
The mass transfer conductivity can be estimated through Ranz and Levenspiel formulas [47,48]:
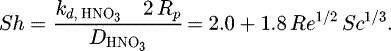 (10)
(10)
Given that the acquisitions are made in a lowly agitated medium, equation (9) comes down to:
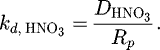 (11)
(11)
Leading to the expression of fe presented in equation (12):
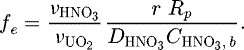 (12)
(12)
In this study, the chemical reaction is considered to be the rate determining step if the value of fe is smaller than 0.05 [45]. In practice, the measured rates will be drawn with the rate 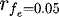 , which is the rate for which fe = 0.05. If the measured rates are smaller than this rate, this means they correspond to the chemical reaction rates. The calculations of
, which is the rate for which fe = 0.05. If the measured rates are smaller than this rate, this means they correspond to the chemical reaction rates. The calculations of 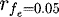 have been realized for nitric acid taking the values below. The retained radius of the particle is a high value, in order to be conservative when affirming that a dissolution rate corresponds to the chemical reaction rate:
have been realized for nitric acid taking the values below. The retained radius of the particle is a high value, in order to be conservative when affirming that a dissolution rate corresponds to the chemical reaction rate:
 |
Fig. 9 Result of the processing of a set of images of a dissolving uranium dioxide fragment in 4.93 mol l−1 nitric acid at ∼343.15 K. |
2.7 Error in the measure of the dissolution rates
The results obtained with this method contain a certain amount of measurement errors. These measurements errors have not been calculated in this work, due to the complication of the identification of the sources of the errors, and of the evaluation and quantification of their contribution to the total measurement errors.
Nevertheless, it is possible to suggest some elements which need to be taken into account for such an assessment. These elements stem from the two steps of the experimental procedure:
-
–
when acquiring the images:
-
•
the calibration of the microscope, which enables the calculation of the size of a pixel,
-
•
the optical quality of the glass and quartz used in the microscope lenses and dissolution cells, which can impact the final quality of the images,
-
•
the acquisition of the images, which are dot matrices filled with the grayscale of the considered pixel. Figure 10 represents a schematization of the disparities which can occurs when representing a real object under the form of dot matrix,
-
•
it is also possible that the object moves during the acquisition, which would distort the measurements of the perimeter and the area.
-
•
-
–
when treating the images:
-
•
the choice of the threshold will necessarily lead to the omission of some pixel belonging to the solid, and vice versa,
-
•
the calculation of the contribution of a border pixel to the total perimeter of the object, which is based on an approximation depending on the neighbouring environment of the pixel.
-
•
Thus, the determination of the measurement error of the method presented in this paper constitutes an interesting and key subject for future developments.
 |
Fig. 10 Comparison between the projected area of a particle and its representation in the form of a dot matrix. |
3 Results and discussion
3.1 Mechanism of the attack of the solid by nitric acid
The first experiment realized consists in observing the attack of a UO2 pellet by optical microscopy. The pellet has been placed on a microscope glass including wells, and a few drops of a 4.93 mol l−1 nitric acid solution at glove box temperature (i.e. 298.15 K) have been introduced in the well.
The uranium dioxide pellet before the addition of the nitric acid solution is presented in Figure 11a. About 1 or 2 s after the addition of the nitric acid solution, the first NOx bubbles appear at the solid-liquid interface, indicating that the reaction has started (Fig. 11b). The reaction keeps running, and the first detachment of macro-bubbles can be observed. These macro-bubbles are formed from coalescence of smaller ones (Fig. 11c). Finally, bubbling comes to an intense stationary regime, and maintaining the focus becomes very complicated. It is possible to see uranium dioxide fragments detaching from the pellet, and falling at the bottom of the vessel (Fig. 11d).
These fragments have been sampled and introduced in another microscope glass well with the same fresh solution as used for the pellet attack. Figure 12 shows the dissolution of the fragments: after more than 22 h of contact with the nitric acid solution, there are still some fragments which are not completely dissolved.
These two series of observations highlight at least a two-steps mechanism for the dissolution of uranium dioxide sintered solids by nitric acid solutions. Based on the observations documented in former articles [30–33,51,52], it is likely that the first step of the attack consists in the formation and development of preferential attack sites. As the result of the development of the biggest sites, as observed in particular in Uriarte and Rainey technical report [52], fragments detached from the solid, which disintegrates. These fragments dissolve much more slowly in the solution, and through a much simpler dissolution mechanism than the pellet one. Indeed, the fragments dissolve without the production of bubbles, likely because of the absence of compatible nucleation sites, and seemingly through a uniform attack. Nevertheless, it is likely that preferential attack sites are formed at the surface of the fragments, and would be closer from the etching pits already reported in previous articles [28,30–33,51]. Thus, these sites cannot be observed by optical microscopy, and do not interfere with the dissolution kinetics measurements.
This last point is of primary importance: one of the main defaults which can be noticed concerning the measurements of dissolution kinetics of uranium dioxide in nitric acid media found in the literature is that they are made at a macroscopic scale, using pellets. At this scale, the evolution of the concentration of dissolving materials in the bulk is practically impossible to relate to the chemical reaction kinetic. Indeed, it results from the complex coupled phenomena of the chemical reaction and mass transport, complicated by others elements such as the reactive surface area evolution during dissolution and bubbling at the surface of the solid [34–37,53–56].
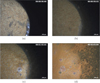 |
Fig. 11 Microscopic observations of the dissolution of a uranium dioxide pellet in nitric acid (corresponding times are indicated on top right of the images). |
 |
Fig. 12 Microscopic observations of the dissolution of the uranium dioxide detached fragments in nitric acid (corresponding times are indicated on top right of the images). |
3.2 Chemical kinetics measurement
The knowledge of the chemical kinetic laws of the dissolution reaction of uranium dioxide in nitric acid media is necessary for determining dissolution residence times at industrial scales. Regarding the complication of the dissolution mechanism at the microscopic scale, the previously reported data, measured at a macroscopic scale [14], seem to be questionable.
The uniform attack and absence of bubbling during the dissolution of the fragments, as well as the possibility of ascertaining the rate determining step during the dissolution rates measurements, encourage their use for chemical kinetics measurements.
3.2.1 Autocatalysis
As presented earlier [14], several experimental observations seem to indicate that the mechanism of the chemical reaction between uranium dioxide and nitric acid is autocatalytic. Nevertheless, the scale at which these observations were made implies that the conclusions drawn could result from the disturbance of other important phenomena like transport phenomena or bubbling [4]. As fragments dissolve in the absence of these potentially disturbing phenomena, the measurements of dissolution rates in solutions containing various amounts of dissolution products allow to conclude on the existence, or not, of an autocatalyzed mechanism. Moreover, the important liquid/solid ratios during these experiments limit catalyzer accumulation, enabling the measurement of the effect of the concentration of dissolution products on the dissolution rates.
Figure 13 shows the dissolution rates of uranium dioxide fragments as a function of the pre-dissolved mass of uranium dioxide, for a 4.73 mol l−1 fresh nitric acid solution at 343.15 K. The nitric acid concentration drawn on this figure corresponds to the initial nitric acid concentration in the solution containing the pre-dissolved mass of uranium dioxide. Thus, its variation is due to the consumption of this reagent by the pre-dissolution of uranium dioxide. Due to the large excess of solution relative to the mass of solid used, the concentration of nitric acid and reaction products can be considered as constant over the time.
It can be seen on this figure that the dissolution rates strongly increase with the increase of the amount of pre-dissolved uranium dioxide, and rapidly reach the limit imposed by mass-transport. Thus, it can be concluded without doubt that the reaction is strongly autocatalyzed.Indeed, considering the global balance equation presented in equation (9), it can be concluded that the total amount of uranium dioxide which can be dissolved in a 4.73 mol l−1 nitric acid solution is about 479 g l−1. This concentration makes any saturation issue hypothetic, since the solubility of uranyl nitrate in water is about 1.27 kg l−1 at 25 °C. The observations of nitric acid gradients around dissolving copper and uranium dioxide particles in this media made by Delwaulle et al. [17,18] also consolidate the conclusion that the slowdown of the increase of the dissolution rates is related to a mass-transport limitation of the nitric acid.
These experiments show that the dissolution rate increases from 2.87 to 70.43 nm s−1, representing about a 25 times increase, while only 10 g l−1 out of the possible 479 g l−1 of uranium dioxide have been pre-dissolved in one liter of a 4.73 mol l−1 nitric acid solution.
The evidence of the existence of an autocatalyzed mechanism also reinforces the interest in measuring dissolution kinetics using microscopic fragments and optical microscopy: the possibility of working with a large excess of solution allows considering that the concentrations of the species, including the products, remain constant over the experiment. Additionally, when the chemical reaction is the rate determining step, the concentrations at the solid/liquid interface can be considered as equal to the concentrations in the bulk. This implies that this method allows, for the first time, measuring the rates of the non-catalyzed reaction and the rates of the catalyzed one separately for various reaction products amounts.
 |
Fig. 13 Dissolution rates as a function of the pre-dissolved mass of uranium dioxide. |
3.2.2 Chemical kinetics of the non-catalyzed reaction
Dissolution rates measurements have been realized in condition of large excess of fresh nitric acid solution at several temperatures and nitric acid concentrations (Fig. 14). The large excess of nitric acid solution is guaranteed by the volume of nitric acid in the well of the dissolution cell, which is about 5, and the fact that the uranium dioxide fragments dissolved for each measurement represent few micrograms of uranium dioxide. The volumetric liquid/solid ratio of these experiments is calculated as presented in equation (12).
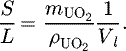 (13)
(13)
Considering a quantity of 10 μg of uranium dioxide dissolved for each run, it results in a final concentration of dissolved uranium of about 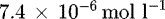 , and a volumetric liquid/solid ratio of 5.5 × 106. These experimental conditions assure that no accumulation of reaction products, responsible for the autocatalysis, occurs in the bulk.
, and a volumetric liquid/solid ratio of 5.5 × 106. These experimental conditions assure that no accumulation of reaction products, responsible for the autocatalysis, occurs in the bulk.
The comparison of the measured dissolution rates with the rate at which the rate determining step switch between chemical reaction and mass-transport (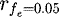 ) shows that these rates have been measured under chemical reaction control. Thus, they correspond to the chemical reaction rates.
) shows that these rates have been measured under chemical reaction control. Thus, they correspond to the chemical reaction rates.
The rate determining step being the chemical reaction, this means that the transportation of the reagents and products through the external diffusion layer is much faster than the chemical reaction.Thus, this confirms that there is neither depletion of the reagents nor accumulation of the products in the external diffusion layer. The absence of accumulation of the reaction products in the external layer is of importance since it justifies the absence of autocatalysis contribution to the measured dissolution rates.
Aberrations appear for some results, as well as important disparities in the measured rates for given conditions. Two facts could explain these defaults:
-
The difficulties for the management of the temperature encountered when using the thermoelectric device probably explain the differences between the dissolution rates measured at the same given nitric acid concentration and temperature with the thermoelectric device and the continuous flow cell.
-
The acquisitions which have been realized under reflected light conditions, which gives poor quality images, due to the little amount of light reflected, and to troubles for maintaining a constant contrast on the images over the experiment. This point definitely encourages to work under transmitted light conditions, which has given much better quality images.
Despite these negative aspects, these measurements give an order of magnitude of the chemical kinetics in presence. They also enable a first estimation of the key parameters of the rate law.
 |
Fig. 14 Non-catalyzed dissolution rates as a function of nitric acid concentration and temperature. |
3.2.3 Partial order of nitric acid in the non-catalyzed reaction
Considering the rate law presented in equation (13) for the non-catalyzed reaction:
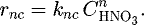 (14)
(14)
A linear regression of ln(r) as a function of 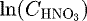 gives the value of the order of nitric acid in the rate law n and the rate constant of the reaction (Fig. 15 and Tab. 1).
gives the value of the order of nitric acid in the rate law n and the rate constant of the reaction (Fig. 15 and Tab. 1).
Based on the data collected in this work, the value of n varies between 3.10 and 4.45, which is in good agreement with previously reported values [14], while the disparities of the measured dissolution rates are likely explaining the variations of the calculated n values.
 |
Fig. 15 Linear regression of ln(r) as a function of |
Non-catalyzed reaction order of nitric acid.
3.2.4 Activation energy of the non-catalyzed reaction
The Arrhenius plot of the dissolution rates (Fig. 16 and Tab. 2) shows the same dependence of activation energy upon temperature as reported in literature, and, not taking into consideration abnormal values, the magnitude of the calculated activation energies are also in good agreement with the literature [14,57–59]. This confirms that this reaction does not follow the Arrhenius law, which could be due to a change in the chemical step limiting the overall dissolution rates.
 |
Fig. 16 Arrhenius plot of the dissolution rates. |
Activation energies (kJ mol−1) of the dissolution reaction.
List of symbols.
4 Conclusions
This study of uranium dioxide dissolution in nitric acid media has been realized by means of in situ optical microscopy. This technique has required the development of devices allowing the observation of the dissolution and control of the temperature which are presented in this paper.
It first enables progress in the understanding of the dissolution mechanism of a macroscopic sintered solid of uranium dioxide. Microscopic observations show that the development of the cracks at the surface of the solid results in its cleavage. There is a large difference in the dissolution of the whole pellet, which disintegrates in smaller fragments with non-addressed complex phenomena and under a short time and the further dissolution of these fragments, which occurs in the absence of bubbling and seems to be uniform.
The simple way the fragments dissolve through has motivated their use for a kinetic study by the means of optical microscopy. Thus, a complete methodology for the treatment of the images of the dissolving fragments has been developed.
The comparison of optical microscopy over the classical macroscopic techniques has shown that it is particularly efficient in other domains, and offers even more advantages in the case of uranium dioxide dissolution in nitric acid media. One of these advantages relates to environmental and safety issues, since this method requires smaller amount of reagent in a comparison with macroscopic ones: this is particularly important in the nuclear chemistry field, where the cost of waste treatment is expensive.
The other points are of primary interest since they concern the specificity of the measurement. The dissolution mechanism of sintered macroscopic uranium dioxide solids is comprised of phenomena which make highly complex, even impossible, any link between measured dissolution kinetics at a macroscopic scale and chemical reaction kinetics. The microscopic experiments presented in this paper show that the dissolution of small fragments occurs in absence of potentially disturbing phenomena, such as bubbling, or non-uniform surface evolution. They also give possibility to easily work with a large excess of liquid, ensuring, when chemical reaction is the rate determining step, that the concentrations of the reagents and products are unchanged over time both in the bulk and at the solid/liquid interface. This means that the concentrations and temperature corresponding to the measured dissolution rates can be accurately known. These last points make microscopy a reliable method for the measurement of the dissolution chemical reaction kinetics.
The series of measurements realized in this work demonstrate that the chemical mechanism is strongly autocatalyzed. The microscopy method enables the measurement of chemical rates of the non-catalyzed reaction, giving a first approximation of the parameters of the rate law. Problems of disparity and some aberrant results imply that further studies will be required in order to measure dissolution rates and determine the parameters of the rate law more accurately, including the catalysed reaction rates.
The measurements presented in this work constitute encouraging preliminary results, which have to be clarified, but remain interesting for approximating some key parameters for modeling the dissolution of uranium dioxide in nitric acid media.
Supplementary Material
Table S1: Uranium dioxide powder analysis.
Table S2: Uranium dioxide pellets manufacturing conditions.
Access hereAcknowledgments
This work was financed by the French Alternative Energies and Atomic Energy Commission and AREVA NC. The authors are thankful to Thibaud Delahaye from the CEA, Nuclear Energy Division, Research Department on Mining and Fuel Recycling Processes, Research Service for Actinide-based Materials Manufacturing Processes, Laboratory of Actinide Conversion Processes Studies, for providing the uranium dioxide pellets and powder.
References
- V. Pillay, R. Fassihi, J. Pharm. Sci. 88, 843 (1999) [CrossRef] [Google Scholar]
- B.R. Bhandari, Y.H. Roos, Carbohydr. Res. 338, 361 (2003) [CrossRef] [Google Scholar]
- A. Marabi et al., Chem. Eng. J. (Amsterdam, Neth.) 139, 118 (2008). [Google Scholar]
- A. Mgaidi et al., Hydrometallurgy 71, 435 (2004) [CrossRef] [Google Scholar]
- R. Gilligan, A.N. Nikoloski, Miner. Eng. 71, 34 (2015) [CrossRef] [Google Scholar]
- H.R. Watling, Hydrometallurgy 140, 163 (2014) [Google Scholar]
- H.R. Watling, Hydrometallurgy 146, 96 (2014) [CrossRef] [Google Scholar]
- J. Steiger, D. Kramer, R. Mönig, J. Power Sour. 261, 112 (2014) [CrossRef] [Google Scholar]
- J. Steiger, D. Kramer, R. Mönig, Electrochim. Acta 136, 529 (2014) [CrossRef] [Google Scholar]
- S.V. Dorozhkin, Ind. Eng. Chem. Res. 35, 4328 (1996) [CrossRef] [Google Scholar]
- M. Joulié, R. Laucournet, E. Billy, J. Power Sour. 247, 551 (2014) [CrossRef] [Google Scholar]
- B. Boullis, Treatment and recycling of spent nuclear fuels. DEN Monographs, (Paris, Éditions du Moniteur, 2008), pp. 7–10 [Google Scholar]
- C. Poinssot et al., Procedia Chem. 7, 349 (2012) [CrossRef] [Google Scholar]
- P. Marc et al., Dissolution of uranium dioxide in nitric acid media: what do we know? EPJ Nuclear Sci. Technol. 3, 13 (2017) [CrossRef] [EDP Sciences] [Google Scholar]
- J.P. Boetker et al., Mol. Pharm. 8, 1372 (2011) [CrossRef] [Google Scholar]
- J. Østergaard et al., J. Pharm. Sci. 100, 3405 (2011) [CrossRef] [Google Scholar]
- C. Delwaulle et al., Chem. Eng. J. (Amsterdam, Neth.) 174, 383 (2011) [Google Scholar]
- C. Delwaulle, Étude de la dissolution du dioxyded'uranium en milieu nitrique: unenouvelle approchevisant à la compréhension des mécanismes interfaciaux. PhD thesis. Institut National Polytechnique de Lorraine, 2011 [Google Scholar]
- M.R. Singh et al., Cryst. Growth Des. 14, 5647 (2014) [CrossRef] [Google Scholar]
- L. Forny, A. Marabi, S. Palzer, Powder Technol. 206, 72 (2011) [Google Scholar]
- S.V. Dorozhkin, J. Cryst. Growth 182, 125 (1997) [CrossRef] [Google Scholar]
- K.V.R. Prasad et al., Int. J. Pharm. (Amsterdam, Neth.) 238, 29 (2002) [Google Scholar]
- S.L. Raghavan et al., J. Pharm. Sci. 91, 2166 (2002) [CrossRef] [Google Scholar]
- S.L. Raghavan et al., J. Pharm. Sci. 92, 439 (2003) [CrossRef] [Google Scholar]
- S. Svanbäck, H. Ehlers, J. Yliruusi, Int. J. Pharm. (Amsterdam, Neth.) 469, 10 (2014) [Google Scholar]
- S. Svanbäck et al., Anal. Chem. (Washington, DC, US) 87, 5041 (2015) [CrossRef] [Google Scholar]
- S. Svanbäck et al., Anal. Chem. (Washington, DC, US) 87, 11058 (2015) [CrossRef] [Google Scholar]
- A. Briggs, Dislocation etching and chemical polishing studies on UO2 single crystals. Technical document Ref. AERE-M 859. (United Kingdom Atomic Energy Authority, 1961) [Google Scholar]
- A. Briggs, Brit. Ceram. Trans. J. 60, 505 (1961) [Google Scholar]
- M. Shabbir, R.G. Robins, J. Nucl. Mater. 25, 236 (1968) [CrossRef] [Google Scholar]
- Y. Zhao, J. Chen, J. Nucl. Mater. 373, 53 (2008) [CrossRef] [Google Scholar]
- Y. Zhao, J. Chen, Radiochim. Acta 96, 467 (2008) [CrossRef] [Google Scholar]
- Y. Zhao, J. Chen, Sci. China. Ser. B. 51, 700 (2008) [CrossRef] [Google Scholar]
- J.Y. Park, O. Levenspiel, Chem. Eng. Sci. 30, 1207 (1975) [CrossRef] [Google Scholar]
- H. Grénman et al., Chem. Eng. Sci. 66, 4459 (2011) [CrossRef] [Google Scholar]
- H. Grénman, T. Salmi, D.Y. Murzin, Rev. Chem. Eng. 27, 53 (2011) [Google Scholar]
- T. Salmi et al., Chem. Eng. Process. 50, 1076 (2011) [CrossRef] [Google Scholar]
- J.S. Weszka, Comput. Vision Graph. 7, 259 (1978) [Google Scholar]
- K.S. Fu, J.K. Mui, Pattern Recogn. 13, 3 (1988) [Google Scholar]
- R.M. Haralick, L.G. Shapiro, Comput. Vision Graph. 29, 100 (1985) [CrossRef] [Google Scholar]
- P.K. Sahoo et al., Comput. Vision Graph. 41, 233 (1988) [CrossRef] [Google Scholar]
- N.R. Pal, S.K. Pal, Pattern Recogn. 26, 1277 (1993) [CrossRef] [Google Scholar]
- N.R. Pal, D. Bhandari, Signal Process. 33, 139 (1993) [CrossRef] [Google Scholar]
- D.E. Mears, Ind. Eng. Chem. Process Des. Dev. 10, 541 (1971) [Google Scholar]
- J.-L. Houzelot, Réacteurs chimiques polyphasés-Couplage réaction/diffusion, in Opérations unitaires. Génie de la réaction chimique (Paris, Techniques de l'ingénieur, 2000) [Google Scholar]
- M. Mohagheghi, G. Bakeri, M. Saeedizad, Chem. Eng. Technol. 30, 1721 (2007) [CrossRef] [Google Scholar]
- J. Villermaux, Génie de la réactionchimique: conception etfonctionnement des réacteurs. Techniques et documentation − Lavoisier, 1985. [Google Scholar]
- O. Levenspiel, Chemical Reaction Engineering (John Wiley & Sons, New York, 1999) [Google Scholar]
- R.S. Ondrejcin, Physical properties of uranium process solutions. Technical document Ref. DP-653.E. I. du Pont de Nemour& Co., 1961. [Google Scholar]
- H.-S. Yeh, G.B. Wills, J. Chem. Eng. Data 16, 76 (1971) [CrossRef] [Google Scholar]
- A. Portnoff, H. Frisby, Comptes-rendus hebdomadaires des séances de l'académie des sciences 250, 1486 (1960) [Google Scholar]
- A.L. Uriarte, R.H. Rainey, Dissolution of high-density UO2, PuO2 and UO2-PuO2 pellets in inorganic acids. Technical document Ref. ORNL-3695 (Oak Ridge National Laboratory, USA, 1965) [Google Scholar]
- L.D. Datsevich, Catal. Today 294, 22 (2005) [Google Scholar]
- B. Blümich et al., Chem. Eng. J. (Amsterdam, Neth.) 134, 35 (2007) [Google Scholar]
- T. Oehmichen, L. Datsevich, A. Jess, Chem. Eng. Technol. 33, 911 (2010) [CrossRef] [Google Scholar]
- T. Oehmichen, L. Datsevich, A. Jess, Chem. Eng. Technol. 33, 921 (2010) [CrossRef] [Google Scholar]
- B. Hermann. Dissolution of unirradiated UO2-pellets in nitric acid. Technical document Ref. 3673. (Karlsruher Institut für Technologie, Germany, 1984) [Google Scholar]
- R.F. Taylor et al., Processing in limited geometry. Part III. The dissolution of uranium dioxide sintered pellets in nitric acid. Technical document Ref. AERE-R 3678. (United Kingdom Atomic Energy Authority, UK, 1962) [Google Scholar]
- R.F. Taylor et al., J. Appl. Chem. 13, 32 (1963) [CrossRef] [Google Scholar]
This code was written in Scilab 5.5.0, free open source software distributed under CeCILL license (GPL compatible), developed by Scilab Enterprises. Available on http://www.scilab.orggr17.
Cite this article as: Philippe Marc, Alastair Magnaldo, Jérémy Godard, Éric Schaer, A method for phenomenological and chemical kinetics study of autocatalytic reactive dissolution by optical microscopy. The case of uranium dioxide dissolution in nitric acid media, EPJ Nuclear Sci. Technol. 4, 2 (2018)
All Tables
All Figures
 |
Fig. 1 Microscopy installation in the glove box. |
| In the text | |
 |
Fig. 2 Pictures of the continuous dissolution cell. |
| In the text | |
 |
Fig. 3 Thermoelectric device for the observation of the dissolution of microscopic solids. |
| In the text | |
 |
Fig. 4 Diagram of the experimental protocol for the study of the autocatalyzed reaction kinetics. |
| In the text | |
 |
Fig. 5 Evolution of the projected area and associated perimeter of a uniformly dissolving particle. |
| In the text | |
 |
Fig. 6 Example of image thresholding and holes filling: original image (a), binarised image (b), and binarised image with holes filled (c). |
| In the text | |
 |
Fig. 7 Example of threshold establishing. |
| In the text | |
 |
Fig. 8 Possible configurations of the neighborhood of a pixel belonging to the perimeter of the object. |
| In the text | |
 |
Fig. 9 Result of the processing of a set of images of a dissolving uranium dioxide fragment in 4.93 mol l−1 nitric acid at ∼343.15 K. |
| In the text | |
 |
Fig. 10 Comparison between the projected area of a particle and its representation in the form of a dot matrix. |
| In the text | |
 |
Fig. 11 Microscopic observations of the dissolution of a uranium dioxide pellet in nitric acid (corresponding times are indicated on top right of the images). |
| In the text | |
 |
Fig. 12 Microscopic observations of the dissolution of the uranium dioxide detached fragments in nitric acid (corresponding times are indicated on top right of the images). |
| In the text | |
 |
Fig. 13 Dissolution rates as a function of the pre-dissolved mass of uranium dioxide. |
| In the text | |
 |
Fig. 14 Non-catalyzed dissolution rates as a function of nitric acid concentration and temperature. |
| In the text | |
 |
Fig. 15 Linear regression of ln(r) as a function of |
| In the text | |
 |
Fig. 16 Arrhenius plot of the dissolution rates. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.