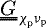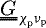| Issue |
EPJ Nuclear Sci. Technol.
Volume 3, 2017
|
|
|---|---|---|
| Article Number | 16 | |
| Number of page(s) | 8 | |
| DOI | https://doi.org/10.1051/epjn/2017011 | |
| Published online | 14 June 2017 | |
https://doi.org/10.1051/epjn/2017011
Regular Article
Local correlated sampling Monte Carlo calculations in the TFM neutronics approach for spatial and point kinetics applications
CEA, DEN, DER, Cadarache,
13108
Saint-Paul Les Durance Cedex, France
⁎ e-mail: axel.laureau@cea.fr
Received:
11
November
2016
Received in final form:
4
March
2017
Accepted:
4
April
2017
Published online: 14 June 2017
These studies are performed in the general framework of transient coupled calculations with accurate neutron kinetics models. This kind of application requires a modeling of the influence on the neutronics of the macroscopic cross-section evolution. Depending on the targeted accuracy, this feedback can be limited to the reactivity for point kinetics, or can take into account the redistribution of the power in the core for spatial kinetics. The local correlated sampling technique for Monte Carlo calculation presented in this paper has been developed for this purpose, i.e. estimating the influence on the neutron transport of a local variation of different parameters such as sodium density or fuel Doppler effect. This method is associated to an innovative spatial kinetics model named Transient Fission Matrix, which condenses the time-dependent Monte Carlo neutronic response in Green functions. Finally, an accurate estimation of the feedback effects on these Green functions provides an on-the-fly prediction of the flux redistribution in the core, whatever the actual perturbation shape is during the transient. This approach is also used to estimate local feedback effects for point kinetics resolution.
© A. Laureau et al., published by EDP Sciences, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The study of power reactor behavior during normal and abnormal operation raises the incentive of modeling the transient phases. This kind of application may require multi-physics tools able to take into account the interaction between the neutronics that provides the fission power source and other physics such as the thermal hydraulics that models the cooling aspects, or mechanics to take into account the core deformation or the pellet-cladding interaction. Each component of these interactions implies complex feedback effects resulting in a strong coupling that requires dedicated appropriate physical models and numerical resolution to balance precision and reasonable computation time. In this frame, some simplifying assumptions in neutron kinetics modeling have to be made since the increase of computation capabilities is not yet sufficient for direct time-dependent Monte Carlo calculations at the full reactor core scale. Hybrid approaches may be used, like improved quasistatic methods, but they require regular updates of the power shape and of the reactivity using precise core calculations.
In this frame, the Transient Fission Matrix (called TFM) approach developed in [1–3] and presented in Section 2 is used here. This approach is based on a conversion to discretized Green functions of the Monte Carlo response in order to perform kinetic calculations without new reference calculation during the transient and thus with a reduced computation time. The TFM approach requires the development of specific interpolation models to perform coupled calculations in order to take into account the evolution of the system's cross-sections during the transient. Previous developments [1] provided interpolation models for PWRs and MSFRs (Molten Salt Fast Reactors), allowing 3D calculations coupled to Computational Fluid Dynamics to be performed. These models are restricted to thermal reactors with a small neutron migration area, or fast reactors without fuel heterogeneities. They are not appropriate for fast reactors with a heterogeneous core and specific developments are required to improve the interpolation. In this paper, we use a sodium fast reactor as an example, in which the low void effect requires a highly discretized geometry with a large sodium plenum and an axial blanket between two fissile zones [4].
Our main focus is on the description of a correlated sampling technique associated to Monte Carlo calculations for the interpolation model used in the spatial TFM approach. Another element developed here is the point kinetics local feedback parameter estimation. The feedback effects considered are the sodium density and the Doppler effects. Instead of estimating the influence of a macroscopic cross-section variation with two independent Monte Carlo calculations, this effect is evaluated using the same neutron histories, leading to a great improvement of the statistical convergence. Correlated sampling in Monte Carlo calculations has been developed previously [5–8] and shows a limitation due to the poor convergence if the perturbation of the source neutron distribution is too large. Previous work [9] has shown the usefulness of the fission matrices to solve this issue on simple systems. The objective of the present work is to develop a neutronic method that is suitable for a sodium cooled reactor core and efficient for time-dependent applications such as transient calculations through a coupling to thermal hydraulics.
The methodology presented here combines the correlated sampling technique and the TFM approach. It is based on a neutron weight modification associated to the origin (density/Doppler) of the perturbation and to its position in the core as presented in Section 3. The calculation of the Green function’s perturbation on a simple test case is detailed in Section 4 to illustrate the approach.
2 TFM approach
2.1 Introduction of the usual fission matrix
Fission matrices are a tool usually used in Monte Carlo calculation codes to accelerate the source convergence [10–13]. This tool is designed to characterize the neutron propagation in a reactor during one generation: the Green function is the system response to a neutron pulse. Using a discretized reactor where the subscripts i, j and k refer to volumes, the amount of neutrons produced per fission in volume i induced by a neutron emitted in volume j corresponds to the fission matrix  element of line i and column j as shown in Figure 1. The subscript k will represent the perturbation position in the next sections. The Fission Matrices correspond to the discretization of the Green functions. By construction, the matrix-vector1 multiplication applied on the generation g source neutron vector Ng corresponds to the propagation of this source neutron over one generation:
element of line i and column j as shown in Figure 1. The subscript k will represent the perturbation position in the next sections. The Fission Matrices correspond to the discretization of the Green functions. By construction, the matrix-vector1 multiplication applied on the generation g source neutron vector Ng corresponds to the propagation of this source neutron over one generation:  . The eigen vector N of the fission matrix is solution of the equation
. The eigen vector N of the fission matrix is solution of the equation 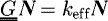 . It corresponds to the equilibrium source neutron distribution in the reactor and is associated to the multiplication factor keff as the eigen value.
. It corresponds to the equilibrium source neutron distribution in the reactor and is associated to the multiplication factor keff as the eigen value.
The fission matrices can be estimated using a Monte Carlo calculation, associating to each calculated neutron its emission position j and recording the neutron production per fission νΣfψ in each volume i (using the fission neutron multiplicity ν, the total fission macroscopic cross-section Σf and the neutron flux ψ). Because of the local information of the neutron transport from j to i, even an estimation using an unconverged source neutron distribution provides the correct eigen vector and consequently the converged source distribution. This feature assumes that the discretization of the fission matrix is fine enough to catch the source neutron distribution variation. For this reason, fission matrices can be employed to estimate the equilibrium source distribution and to improve the source convergence. If the fission matrix is estimated using a converged source neutron distribution, there is no assumption on the mesh precision since the source neutron distribution inside volume j is the actual distribution.
 |
Fig. 1 Neutron propagation over one generation, and representation of the fission matrix element ij: neutron production in volume i induced by an incoming source neutron emitted in j. |
2.2 TFM presentation
This section presents a general overview of the TFM approach. More details and a validation of the TFM approach on nuclear systems such as the Flattop and the Jezebel experiments can be found in references [1–3]. Note that the objective of this approach is not to produce a reference solution such as a direct kinetic Monte Carlo calculation, but to provide a precise spatial kinetic modeling with a reasonable computation time. The error associated to this method can be evaluated by comparison with full Monte Carlo calculations, on snapshots during a transient calculation, or with direct kinetic Monte Carlo when such a code will be available in the future. Comparisons with direct kinetic Monte Carlo without thermal feedbacks have already been performed and are detailed in [1].
In order to perform transient calculations using the fission matrices, two pieces of information have to be added to the usual fission matrices: the distinction between delayed and prompt neutrons and the temporal aspect.
2.2.1 Prompt and delayed neutrons
Delayed (labelled “d”) and prompt (labelled “p”) neutrons have different emission spectra and consequently distinct behaviors in the reactor. Moreover, the production of delayed neutrons is different from that of prompt neutrons since their multiplicities are not the same. For these reasons, four different matrices have to be calculated to take into account each case: 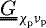 ,
, 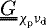 ,
, 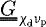 and
and 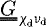 . They correspond to the transport probabilities using the emission spectrum χp or χd and the neutron production multiplicity νp or νd. These matrix calculations are performed with a Monte Carlo neutronic code using the same approach as for the usual fission matrices, the code being modified to link the origin of their emission (prompt or delayed) to the transported neutrons and to score separately νpΣfψ and νdΣfψ at each interaction. Different Monte Carlo codes may be used, and the present paper is based on calculations done with a modified version of the Serpent2 code [14].
. They correspond to the transport probabilities using the emission spectrum χp or χd and the neutron production multiplicity νp or νd. These matrix calculations are performed with a Monte Carlo neutronic code using the same approach as for the usual fission matrices, the code being modified to link the origin of their emission (prompt or delayed) to the transported neutrons and to score separately νpΣfψ and νdΣfψ at each interaction. Different Monte Carlo codes may be used, and the present paper is based on calculations done with a modified version of the Serpent2 code [14].
2.2.2 Temporal aspect
The second factor required to perform neutron kinetics with the fission matrices is the temporal aspect of the neutron propagation. Considering that the neutron transport time is negligible compared to the delayed neutron precursor lifetime, only the prompt neutron fission to fission time matrix 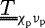 is needed. This matrix contains the average propagation time for a source neutron from j to i.
is needed. This matrix contains the average propagation time for a source neutron from j to i.
2.2.3 Neutron kinetics equations
As developed in [1–3], this approach allows the estimation of kinetics parameters and the calculation of neutron kinetics. An importance map of the reactor is accessible using the transposed fission matrices (backward transport): the eigen vector solution of this adjoint problem corresponds to the adjoint neutron source distribution. This importance map is used in association with the fission and time matrices to calculate the effective fraction of delayed neutrons βeff and the effective lifetime leff. This property has been used to validate the approach [3]. The neuron kinetics equations can be developed using Np(t), the prompt neutron production at time t, and 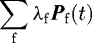 , the delayed neutron production induced by the decay of the precursors.2 These are balance equations:
, the delayed neutron production induced by the decay of the precursors.2 These are balance equations:
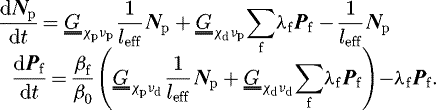 (1)
(1)
Note that these equations do not use directly the effective fraction of delayed neutrons. The importance of the delayed neutrons is taken into account through the 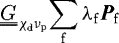 matrix that deals with the probability for a delayed neutron to produce a new prompt neutron, and the difference between this production and the total prompt neutron shape is then explicitly modeled. Concerning the effective lifetime used in
matrix that deals with the probability for a delayed neutron to produce a new prompt neutron, and the difference between this production and the total prompt neutron shape is then explicitly modeled. Concerning the effective lifetime used in 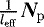 , this formulation assumes that the prompt neutron shape is near to the equilibrium, which is correct in most of the transients studied here. The neutron lifetime evolution during the transient is correctly taken into account, but an assumption is done here considering that this prompt neutron lifetime is small compared to the transient characteristic time constant.
, this formulation assumes that the prompt neutron shape is near to the equilibrium, which is correct in most of the transients studied here. The neutron lifetime evolution during the transient is correctly taken into account, but an assumption is done here considering that this prompt neutron lifetime is small compared to the transient characteristic time constant.
2.3 Fission matrix interpolation
During a transient calculation, the reactor composition and temperature shape can evolve. Thus, the TFMs 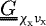 and
and 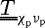 must be estimated in order to integrate the neutron kinetics equation (1). Different interpolation models have been developed in previous work [1–3]. These models are based on the combination of distinct calculations: a reference case and a case with a global modification of the system such as the coolant density, the fuel temperature, the boron composition or the control rod position in the reactor. All the matrices of the TFM approach are estimated only once, before the transient calculation.
must be estimated in order to integrate the neutron kinetics equation (1). Different interpolation models have been developed in previous work [1–3]. These models are based on the combination of distinct calculations: a reference case and a case with a global modification of the system such as the coolant density, the fuel temperature, the boron composition or the control rod position in the reactor. All the matrices of the TFM approach are estimated only once, before the transient calculation.
Finally, during the transient calculation, these uniformly perturbed matrices are used to interpolate the matrices corresponding to the real state of the reactor and are used to compute the neutron kinetics. The perturbation in the reactor is usually not homogeneous; for example, the reactor may have a complex density distribution. The interpolated matrix then combines on the fly the local neutron transport information contained in the different reference matrices as detailed in this article in Section 4.3.
For a PWR assembly [1], a very good agreement on the flux redistribution and keff prediction has been obtained on the control rod up-down movement, from two distinct calculations (rods in and rods out), all the intermediate states being successfully interpolated with a reduced calculation time (around 1/100 s). For 3D coupled calculations of a Molten Salt Fast Reactor [1,2], a very good agreement has been obtained with direct Monte Carlo calculations, using an improved interpolation scheme based on the absorption localization additionally to the fissions to take into account the fuel salt density effect. These two cases show that the TFM approach may be used for thermal spectrum as well as for fast spectrum reactors. However, this interpolation scheme is not appropriate for a sodium density variation in the sodium plenum: even without absorption, a variation of the density has a significant impact on the neutron leakage. For this reason, the local information contained in the fission matrix is not enough to obtain an appropriate interpolation model. Instead of “source neutron transfer probability from volume j to volume i”, the information required is the “source neutron transfer probability from volume j to volume i assuming a perturbation in the crossed volume k”.
3 Monte Carlo and correlated sampling
In Monte Carlo codes, the estimation of the influence of a local variation of the macroscopic cross-sections can be performed using two independent calculations with a local modification of the media. Two drawbacks render this approach inappropriate here:
-
since the variation of the parameters of interest is not large compared to the statistical error, the estimation would require a large number of simulated neutrons;
-
in order to estimate the effect of hundreds of local perturbations, hundreds of calculations would be required and the computation cost would be prohibitive.
A second option consists in using a single calculation to estimate both the reference and the perturbed configurations using the correlated sampling technique. To each neutron is associated one (or more if several perturbations) perturbed weight, which is modified at each interaction in order to take into account the medium modification. The equivalent “perturbed” neutron follows the same series of interactions as the “unperturbed” one, so that the sampling is the same, but its weight is modified accordingly. This evolution of the perturbed weight is a multiplicative process, all the contributions of all the interactions during the neutron’s life are staked and used to weight the scores.
Three different materials are associated to each cell of the geometry in this study: a reference one, one with a lower coolant (sodium) density, and one with a higher temperature (Doppler broadening of the cross-sections). The neutron transport corresponds to the interactions with the reference material, the perturbed transport being reconstructed using the perturbed weight attached to the neutron history wpert. Depending on the perturbation of the interaction probability, the perturbed neutron weight evolves and is used to score the parameters of interest such as 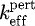 with the same statistical uncertainty as keff. In this way, a small quantity like the reactivity variation linked to the local perturbation
with the same statistical uncertainty as keff. In this way, a small quantity like the reactivity variation linked to the local perturbation 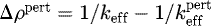 can be estimated directly, without using the difference of two numbers with their own statistical error.
can be estimated directly, without using the difference of two numbers with their own statistical error.
Note that this correlated sampling technique assumes that the nucleus already exists in the core (i.e. control rod insertion) and that the amplitude of the perturbation is not too important to avoid large modifications of the neutron weight. For this reason, perturbations are limited to a few percents on materials densities and this approach cannot be directly used for effects such as control rod movement. The interaction of a neutron with an element that does not exist in the perturbed version of the reactor will create neutrons with a perturbed weight equal to zero.
As discussed below, two processes have to be tracked during the Monte Carlo calculation, viz. the sampling of the distance between two interactions and the interaction type (scattering, fission, etc.). Finally, using a perturbed weight, the effect of a local modification of the materials can be taken into account in the fission matrices.
3.1 Next interaction distance sampling
For a given neutron energy, the distance between two interactions is sampled using the normalized density distribution: 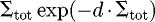 where Σtot is the total cross-section at the neutron energy and d the interaction position. The perturbed distance is calculated using the perturbed macroscopic total cross-section
where Σtot is the total cross-section at the neutron energy and d the interaction position. The perturbed distance is calculated using the perturbed macroscopic total cross-section 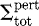 instead of Σtot. Thus, since the perturbed transport is based on that of the reference (i.e. uses the same reference sampled distance d), the perturbed neutron weight is multiplied by the ratio of the probability of reaching this position:
instead of Σtot. Thus, since the perturbed transport is based on that of the reference (i.e. uses the same reference sampled distance d), the perturbed neutron weight is multiplied by the ratio of the probability of reaching this position:
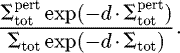 (2)
(2)
For example, if 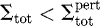 , the neutron averaged sampled distance is smaller in the perturbed system. For this reason, if the sampled distance tends towards 0, the neutron perturbed weight will increase by
, the neutron averaged sampled distance is smaller in the perturbed system. For this reason, if the sampled distance tends towards 0, the neutron perturbed weight will increase by 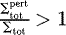 . In this way, the future interactions (scattering, fission, etc.) of the neutron will be scored with an increased weight due to the contribution of this “transport event”, and the weighted neutron is representative of the perturbed system.
. In this way, the future interactions (scattering, fission, etc.) of the neutron will be scored with an increased weight due to the contribution of this “transport event”, and the weighted neutron is representative of the perturbed system.
3.2 Interaction type sampling
Once the position of the interaction is sampled using the total cross-section, the nucleus and the interaction type are also sampled (fission, absorption, elastic and inelastic scattering, etc.).
Assuming a sampled reaction r on nucleus n, the probability of this reaction among all the possible reactions is 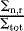 . The probability of the same reaction on the same nucleus with the perturbed material is
. The probability of the same reaction on the same nucleus with the perturbed material is 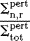 . Finally, the neutron perturbed weight is multiplied by:
. Finally, the neutron perturbed weight is multiplied by:
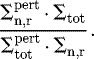 (3)
(3)
3.3 Perturbed neutron source
The Monte Carlo calculation works with batches of neutrons corresponding to different generations with a source distribution given by the fission position of the previous batch. The neutron source distribution in the perturbed reactor is different from the reference distribution. The difference between those distributions is taken into account by the perturbed weight of the neutron at its creation, but this weight is not initially known. The initial neutron weight is preset with the perturbed weight of its father, i.e. the neutron that has produced the fission. An issue with that technique is the progressive increase of the perturbed weight dispersion. Each neutron has an independent life in the reactor; then if there is no clustering (as expected) of the neutrons, they will not mix their perturbed weights and some of the neutrons will have a prohibitive weight. These neutrons will make the contribution of the other neutrons negligible. For this reason, the number of generations used to propagate the source neutron weight is limited according to a sensitivity study done for each application case.
For the TFM application, the perturbed source distribution is not required. As already explained, if the mesh used for the fission matrices is fine enough to model the flux redistribution, the eigen vector will be correct since the information contained in the fission matrix is the local propagation of the neutrons. For this reason, the results presented here use a perturbed weight initialized to 1 and do not propagate the perturbed weight of the ancestors.
4 Correlated sampling application to TFM
4.1 Application case description
In order to illustrate the estimated matrices, a simple one-dimensional case derived from as SFR assembly with only three areas (fissile, sodium and B4C) has been considered in this paper and is represented in Figure 2. This simplified case is also used in [15], together with a more complex case representative of an ASTRID [16] assembly, for a validation of this approach based on comparisons with direct Monte Carlo and ERANOS calculations. Note that the fuel region here corresponds to an assembly homogeneisation so that it contains fuel, sodium and steel. The geometry boundary condition is a radial reflexion and an axial leakage.
The material temperatures and isotopic reference compositions are given in Table 1. These compositions are considered radially homogeneous so that, for example, the B4C area contains sodium and steel.
 |
Fig. 2 Simple case geometry description in cm. |
Material temperatures and compositions – 1024 atoms per cm3.
4.2 Global fission matrix interpolation
Using the correlated sampling approach, we have obtained scores corresponding to different perturbed states of the reactor. Typically, in order to run transient coupled calculations, the perturbations of interest concern the coolant density and the fuel temperature. Using a perturbed weight for each neutron, it is thus possible to generate the variation of the fission matrices for each element i,j according to a global modification of the sodium density and of the temperature in a sodium cooled fast reactor. This is stored respectively in the variation matrices 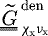 and
and 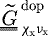 . Even if the matrices of interest for neutronic calculations are the fission matrices, these variation matrices will be very useful to interpret the effect of a perturbation on the core.
. Even if the matrices of interest for neutronic calculations are the fission matrices, these variation matrices will be very useful to interpret the effect of a perturbation on the core.
In the following, a density dependency with a variation of −1% and a temperature dependency with a variation of +300 K (representative of the order of magnitude of the expected variation during transients) are estimated in this way. Based on the information contained in these two variation matrices, any other global perturbation can be interpolated using a linear dependency on the sodium density Δρsodium, and a logarithmic dependence on the fuel temperature Tmean using equation (4).
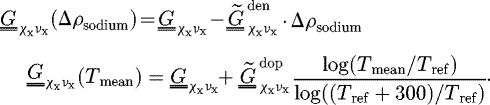 (4)
(4)
Figure 3 presents the reference fission matrix 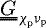 (left) and its variation with the density (middle) and the Doppler effects (right). The neutron propagation is directly visible on this fission matrix (left). Each emission position corresponds to a column, and for this column, the position of the neutrons produced by fissions corresponds to the different lines. We can see that all the fissions come from and occur in the fissile zone with an index between 0 and 30. The probability of generating a new source neutron is reduced close to the small values of index j and i due to the leakage at the bottom of the assembly. On the contrary, around bin 30, the sodium is a neutron reflector so that the source neutron production is less impacted by the end of the fuel area.
(left) and its variation with the density (middle) and the Doppler effects (right). The neutron propagation is directly visible on this fission matrix (left). Each emission position corresponds to a column, and for this column, the position of the neutrons produced by fissions corresponds to the different lines. We can see that all the fissions come from and occur in the fissile zone with an index between 0 and 30. The probability of generating a new source neutron is reduced close to the small values of index j and i due to the leakage at the bottom of the assembly. On the contrary, around bin 30, the sodium is a neutron reflector so that the source neutron production is less impacted by the end of the fuel area.
Concerning the density effect (middle), the neutron production is reduced on the diagonal of the matrix (for a target volume i close to the origin volume j), and the production is relocated far from the neutron emission position. This effect is due to a larger mean free path resulting from the decreased sodium density. Near the boundary between the fuel area and the sodium, the strong negative feedback is explained by more neutron leakage to the B4C.
Concerning the Doppler effect (right panel), the impact on the neutron propagation is not a relocalisation such as with the density change, but a negative global feedback due to a modification of the fission-absorption ratio and spectrum. The effect is larger near the sodium area.
 |
Fig. 3 Fission matrix |
4.3 Local fission matrix interpolation
In usual applications implying a coupling with other physics like thermal hydraulics, a global perturbation is not enough to model the complex variations on the temperature distribution in the core. The local feedback effect has to be estimated using local perturbed weights.
In this work, we have chosen to superimpose an arbitrary mesh (associated to the subscript k) on the geometry in order to make the local variation correspond to a position in the geometry. In this way, even for a pin-discretized geometry, if the k volumes represent average axial sections of the assembly, the influence of perturbations in one of the physical sub-volumes contained in k (such as the coolant) can be taken into account with a small number of volumes k. This mesh can typically correspond to an axial discretization of the different individual assemblies, or can represent a gathering of periodic or neighboring assemblies depending on the core geometry.
For each neutron, the neutron weight evolution is scored at each interaction in a vector corresponding to the different perturbations in each location k. Depending on the interaction position k, the associated weight of this vector is modified. If the neutron source perturbation is taken into account, a vector of such weight-vectors is used to memorize the final cumulative weight of each previous neutron generation for each perturbation position k.
Finally, specific variation matrices are estimated for each volume k, 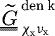 and
and 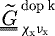 , representing the variations of
, representing the variations of 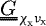 due to the modifications of the reactor in k. Then, for any perturbation distribution depending on k such as Δρsodium (k) and the fuel temperature T (k), the fission matrices are interpolated using equation (5).
due to the modifications of the reactor in k. Then, for any perturbation distribution depending on k such as Δρsodium (k) and the fuel temperature T (k), the fission matrices are interpolated using equation (5).
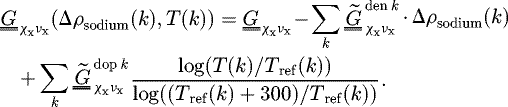 (5)
(5)
The variations of the fission matrices are calculated for each local perturbation by tracking the contribution of each local volume to the perturbation of the neutrons. Figure 4 illustrates the variation of the 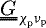 fission matrix, due to a local variation of −1% sodium density and +300 K at different positions in the fuel and in the sodium areas.
fission matrix, due to a local variation of −1% sodium density and +300 K at different positions in the fuel and in the sodium areas.
We can see with the sodium density feedback (top) that the main effect is a relocalisation of the source neutron production to the other side of the perturbation position in k: reduction of the production if (i and j) > k or (i and j) < k. This effect is observable on the left and middle matrices and is due to the local increase of the neutron free path. The neutron spectrum also becomes harder, increasing the neutron production (positive feedback). With a perturbation k in the sodium area (right panel), the leakage from the fuel to the B4C increases, reducing the source neutron production in the fuel close to the sodium (production in j or target in i close to bin 30).
Concerning the Doppler effect (bottom), the impact is a large strip that depends mainly on the i position. We can see a line on the perturbation position i = k: the Doppler effect locally modifies the fission-absorption ratio and increases the total macroscopic cross-section, leading to a global reduction of the fissions produced at the other positions i ≠ k.
 |
Fig. 4 Fission matrix |
5 Calculation of point kinetics parameters
The perturbative TFM approach has been designed to perform low-cost transient calculations with an optimized spatial neutronics model. However, it is also possible to use it to calculate the local feedback effects for point kinetics applications: the eigen values of the different local contributions such as 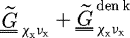 .
.
For a full core calculation with hundreds of assemblies, the computation time can become prohibitive. Two optimizations can provide a significant speedup of the calculation using:
-
an adaptative mesh reducing the mesh size when possible since the latter does not need the same precision in each part of the geometry;
-
and sparse matrices since the variation matrices (e.g. Fig. 4) contain a lot of zeros.
If required, a quasistatic scheme can also be used. The flux shape and the point kinetics local feedbacks described here would be recalculated at different time steps, and a point kinetics model would be used between these time steps.
Figure 5 presents the feedback coefficients estimated using TFM. The density coefficient (top) corresponds to the linear reactivity variation associated to a sodium density decrease of 1%. The Doppler coefficient (bottom) is the logarithmic coefficient of the reactivity variation associated to a temperature modification.
For a sodium density decrease, the neutron spectrum becomes harder so that the neutron production increases (positive feedback) if the perturbation is far from the fuel area boundary. At the bottom of the core, a reduction of the sodium density implies an increase of the leakage from the core, and thus a negative feedback effect. The same effect exists at the top of the fissile area, but is reduced (−0.3 vs. −0.9 pcm/%/cm) due to the neutron reflexions from the sodium. In the sodium area (50 up to 75 cm), a decrease of the sodium density implies a direct increase of the neutron leakage to the B4C, explaining the large value obtained (−1.2 pcm/%/cm). Note that since there is no radial leakage, the localisation of the sodium density variation (in the sodium area) has no impact on the probability that a neutron is absorbed by the B4C. This phenomenon is directly visible in this figure through the constant feedback coefficient value. Finally, in the B4C, the feedback effects quickly decrease due to the reduction of the neutron flux and of the neutron importance.
Concerning the Doppler effect, the contribution in the fuel area is negative since the resonance broadening favors the absorptions, and it is slightly positive close to the bottom of the geometry since the global reaction rate increase limits the leakages. A skin effect is observable between the fissile area and the sodium due to the spectrum shift of the reflected neutrons.
 |
Fig. 5 Sodium density and Doppler feedback distribution, computed using TFM with 60 bins. |
6 Conclusion
The correlated sampling technique discussed in this paper proves to be a powerful tool that can provide perturbed fission matrices. The spatial neutron kinetic TFM approach was developed and coupled to the thermal hydraulics in previous work. With this new development, the application scope of the method extends to fast reactors with significant heterogeneities.
The sensitivities of the crossed volumes are accurately taken into account in the estimation of the neutron transport probability from each neutron origin to the targeted volumes. This perturbed TFM approach based on the correlated sampling technique has been implemented in the Serpent2 code and tested on a simplified case representative of a sodium fast reactor to illustrate the capability to predict the effect of a local medium modification on the fission matrices for a heterogeneous fast reactor. Feedbacks from perturbations on the sodium density and the temperature have been calculated. The interpolation model described here generates the perturbed matrices by combining a sum of local contributions considering a linear and a logarithmic dependency for the density and the Doppler effects, respectively.
A further development of this approach is the comparison of the results obtained with direct Monte Carlo and ERANOS calculations. This has been done on an ASTRID-like assembly and is discussed in [15]. Other future developments concern the utilisation of sparse matrices to optimise full core calculations, and the development of a multi-scale scheme associating coarse and fine meshes for the interpolation model in order to limit the cross effects between the local contributions.
Acknowledgments
The authors wish to thank the IN2P3 department of the CNRS (National Center for Scientific Research) for its support during the initial development of the TFM approach. We are also very thankful to our colleagues Elisabeth Huffer for her help during the translation, Elsa Merle-Lucotte for her help with the rereading and Adrien Bidaud for discussions.
References
- A. Laureau, Développement de modèles neutroniques pour le couplage thermohydraulique du MSFR et le calcul de paramètres cinétiques effectifs, Ph.D. thesis, Université Grenoble Alpes, 2015 [Google Scholar]
- A. Laureau, M. Aufiero, P. Rubiolo, E. Merle-Lucotte, D. Heuer, Coupled neutronics and thermal-hydraulics transient calculations based on a fission matrix approach: application to the Molten Salt Fast Reactor, in Joint International Conference on Mathematics and Computation, Supercomputing in Nuclear Applications and the Monte Carlo Method (M&C+SNA+MC 2015), Nashville, USA (2015) [Google Scholar]
- A. Laureau, M. Aufiero, P. Rubiolo, E. Merle-Lucotte, D. Heuer, Transient fission matrix: kinetic calculation and kinetic parameters βeff and Λeff calculation, Ann. Nucl. Energy 85, 1035 (2015) [CrossRef] [Google Scholar]
- P. Sciora, D. Blanchet, L. Buiron, B. Fontaine, M. Vanier, F. Varaine, C. Venard, S. Massara, A.-C. Scholer, D. Verrier, Low void effect core design applied on 2400 MWth SFR reactor, in International Congress on Advances in Nuclear Power Plants (ICAPP), 2011 (2011) [Google Scholar]
- U. Feldman, E. Gelbard, R. Blomquist, Monte Carlo small-sample perturbation calculations, Tech. Rep. (Argonne National Lab., IL, USA, 1983) [Google Scholar]
- H. Rief, Generalized Monte Carlo perturbation algorithms for correlated sampling and a second-order Taylor series approach, Ann. Nucl. Energy 11, 455 (1984) [CrossRef] [Google Scholar]
- F.X. Gallmeier, A New MCNP Option: KCORR – the use of the correlated sampling method to study reactivity effects due to changes of a reactor arrangement, Nucl. Sci. Eng. 120, 102 (1995) [CrossRef] [Google Scholar]
- E. Brun, F. Damian, C. Diop, E. Dumonteil, F. Hugot, C. Jouanne, Y. Lee, F. Malvagi, A. Mazzolo, O. Petit et al., Tripoli-4®, CEA, EDF and AREVA reference Monte Carlo code, Ann. Nucl. Energy 82, 151 (2015) [CrossRef] [Google Scholar]
- W. Bernnat, A Monte Carlo technique for local perturbations in multiplying systems, in Proc. NEACRP Specialist Meeting, ANL-75-2 (1974), p. 261 [Google Scholar]
- J. Dufek, W. Gudowski, Fission Matrix based Monte Carlo criticality calculations, Ann. Nucl. Energy 36, 1270 (2009) [CrossRef] [Google Scholar]
- D. Kornreich, D. Parsons, Time–eigenvalue calculations in multi-region Cartesian geometry using Green’s functions, Ann. Nucl. Energy 32, 964 (2005) [CrossRef] [Google Scholar]
- S. Carney, F. Brown, B. Kied-rowski, W. Martin, Fission matrix capability for MCNP Monte Carlo, Trans. Am Nucl. Soc. 107, 494 (2012) [Google Scholar]
- S. Carney, F. Brown, B. Kiedrowski, W. Martin, Theory and applications of the fission matrix method for continuous-energy Monte Carlo, Ann. Nucl. Energy 73, 423 (2014) [CrossRef] [Google Scholar]
- J. Leppänen, M. Pusa, T. Viitanen, V. Valtavirta, T. Kaltiaisenaho, The Serpent Monte Carlo code: status, development and applications in 2013, Ann. Nucl. Energy 82, 142 (2015) [Google Scholar]
- A. Laureau, L. Buiron, F. Bruno, Towards spatial kinetics in a low void effect sodium fast reactor: core analysis and validation of the TFM neutronic approach, EPJ Nuclear Sci. Technol. 3, 17 (2017) [CrossRef] [EDP Sciences] [Google Scholar]
- B. Fontaine et al., Sodium-cooled fast reactors: the ASTRID plant project, in Proc. GLOBAL, 2011 (2011), pp. 11–16 [Google Scholar]
Cite this article as: Axel Laureau, Laurent Buiron, Bruno Fontaine, Local correlated sampling Monte Carlo calculations in the TFM neutronics approach for spatial and point kinetics applications, EPJ Nuclear Sci. Technol. 3, 16 (2017)
All Tables
All Figures
 |
Fig. 1 Neutron propagation over one generation, and representation of the fission matrix element ij: neutron production in volume i induced by an incoming source neutron emitted in j. |
| In the text | |
 |
Fig. 2 Simple case geometry description in cm. |
| In the text | |
 |
Fig. 3 Fission matrix |
| In the text | |
 |
Fig. 4 Fission matrix |
| In the text | |
 |
Fig. 5 Sodium density and Doppler feedback distribution, computed using TFM with 60 bins. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.