| Issue |
EPJ Nuclear Sci. Technol.
Volume 2, 2016
|
|
|---|---|---|
| Article Number | 11 | |
| Number of page(s) | 14 | |
| DOI | https://doi.org/10.1051/epjn/e2016-50002-7 | |
| Published online | 18 March 2016 | |
https://doi.org/10.1051/epjn/e2016-50002-7
Regular article
Comparison of SERPENT and SCALE methodology for LWRs transport calculations and additionally uncertainty analysis for cross-section perturbation with SAMPLER module
Institute for Industrial, Radiophysical and Environmental Safety (ISIRYM), Universitat Politècnica de València, Camí de Vera s/n, 46022, Valencia, Spain
⁎ e-mail: alabarile@iqn.upv.es
Received:
28
April
2015
Received in final form:
30
October
2015
Accepted:
12
January
2016
Published online:
18
March
2016
In nuclear safety research, the quality of the results of simulation codes is widely determined by the reactor design and safe operation, and the description of neutron transport in the reactor core is a feature of particular importance. Moreover, for the long effort that is made, there remain uncertainties in simulation results due to the neutronic data and input specification that need a huge effort to be eliminated. A realistic estimation of these uncertainties is required for finding out the reliability of the results. This explains the increasing demand in recent years for calculations in the nuclear fields with best-estimate codes that proved confidence bounds of simulation results. All this has lead to the Benchmark for Uncertainty Analysis in Modelling (UAM) for Design, Operation and Safety Analysis of LWRs of the NEA. The UAM-Benchmark coupling multi-physics and multi-scale analysis using as a basis complete sets of input specifications of boiling water reactors (BWR) and pressurized water reactors (PWR). In this study, the results of the transport calculations carried out using the SCALE-6.2 program (TRITON/NEWT and TRITON/KENO modules) as well as Monte Carlo SERPENT code, are presented. Additionally, they have been made uncertainties calculation for a PWR 15 × 15 and a BWR 7 × 7 fuel elements, in two different configurations (with and without control rod), and two different states, Hot Full Power (HFP) and Hot Zero Power (HZP), using the TSUNAMI module, which uses the Generalized Perturbation Theory (GPT), and SAMPLER, which uses stochastic sampling techniques for cross-sections perturbations. The results obtained and validated are compared with references results and similar studies presented in the exercise I-2 (Lattice Physics) of UAM-Benchmark.
© A. Labarile et al., published by EDP Sciences, 2016
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
This work takes part in the framework of the Organization for Economic Cooperation and Development/Nuclear Energy Agency (OECD/NEA) Benchmark, for Uncertainty Analysis in Best-Estimate Modelling (UAM), for Design, Operation and Safety Analysis of LWRs. The groundwork was launched in 2005 with the objective to prepare a benchmark work program with steps (exercises) that would be needed to define the uncertainty and modelling task for the development of uncertainty analysis methodologies, for multi-physics and multi-scale simulation. The final goal will create a roadmap along with schedule and organization, for the development and validation of method and codes required for uncertainty and safety analysis in LWR design [1].
Reference systems and scenarios for coupled code analysis are defined to study the uncertainty effects for all stages of the system calculations. Measured data from plant operation and experimental reference data are available for the chosen scenarios. The full chain of uncertainty propagation from basic data, engineering uncertainties, across different scales (multi-scale), and physics phenomena (multi-physics) is tested on some benchmark exercises for which experimental data are available and for which the power plant details have been released. The general frame of the OECD UAM LWR Benchmark consists of three phases with different exercises for each phase: Phase 1 (neutronics phase), Phase 2 (core phase) and Phase 3 (system phase). The focus of Phase 1 is on propagating uncertainties in stand-alone neutronics calculations and consists of the following three exercises:
-
Exercise I-1: “Cell Physic” focused on the derivation of the multigroup microscopic cross-section libraries and associated uncertainties;
-
Exercise I-2: “Lattice Physics” focused on the derivation of the few-group macroscopic cross-section libraries and associated uncertainties;
-
Exercise I-3: “Core Physics” focused on the core steady state stand-alone neutronics calculations and associated uncertainties.
The present paper deals with Cell Physic and Lattice Physics exercises, determining uncertainties associated with basic nuclear data, method and modelling approximation used in lattice physics codes.
This document is structured as follows: the Introduction in Section 1. Section 2 is focused on the description of the codes. The description of the models is shown in Section 3. The results for different codes are presented in Section 4. Finally, the conclusions are shown in Section 5.
2 Codes description
2.1 Transport calculation
In this work, two- and three-dimensional lattice codes (deterministic and stochastic) were selected to perform transport calculations: SCALE-6.2 with TRITON/NEWT and TRITON/KENO modules and SERPENT-2.1.22 code.
The SCALE code system [2] is a collection of computational modules whose execution can be linked by various “sequences” to solve a wide variety of applications.
TRITON (Transport Rigor Implemented with Time-dependent Operation for Neutronics depletion) is a multipurpose SCALE control module for transport and depletion calculations for reactor physics applications. TRITON is used to provide automated, problem-dependent cross-sections processing followed by multigroup neutron transport calculation for one-, two- or three-dimensional configuration [3].
NEWT (New ESC-based Weighting Transport code) is a two-dimensional (2D) discrete ordinates transport code developed at Oak Ridge National Laboratory. It is based on the Extended Step Characteristic (ESC) approach for spatial discretization in an arbitrary mesh structure. This discretization scheme makes NEWT an extremely powerful and versatile tool for deterministic calculation in real-world non-orthogonal problem domains. The NEWT computer code has been developed to run on SCALE. Thus, NEWT uses AMPX-formatted cross-sections processed by other SCALE modules [4].
The implemented methodology of these coupled modules of SCALE allows carrying out transport calculation with the computation of energy collapsed and homogenized macroscopic cross-sections. In TRITON, NEWT is used to calculate weighted burnup-dependent cross-sections that are employed to provide localized fluxes used for multiple depletion regions. Additionally, TRITON uses a two-pass cross-section update approach to perform fuel assembly burnup calculations and generates a database of cross-sections and other burnup-dependent physics data that can be used for full-core analysis [5].
KENO is a functional module in the SCALE system and a Monte Carlo criticality program used to calculate the keff of three-dimensional (3D) system [6]. It uses the SCALE Generalized Geometry Package (SGGP), which offers a powerful geometric representation. KENO was one of the oldest criticality safety analysis tools in SCALE. The primary purpose of its employment in this work is to determine keff calculations and compare KENO results with TRITON/NEWT and SERPENT-2 calculation.
SERPENT is a three-dimensional continuous-energy code, based on the Monte Carlo method, for reactor physics burnup calculation [7,8]. The SERPENT project started in 2004 at the VTT Technical Research Centre of Finland. The first version of the code was available to universities and research institutes from 2008 and currently it is still under development. The suggested applications of SERPENT include, among other applications, the spatial homogenization and constant group generation for deterministic reactor calculations and the validation of deterministic lattice transport codes.
2.2 Sensitivity and uncertainty calculation
Sensitivity analysis and propagation of uncertainties of cross-sections have been carried out using TSUNAMI and SAMPLER modules.
TSUNAMI-2D (Tools for Sensitivity and Uncertainty Analysis Methodology Implementation in Two Dimension) is a SCALE sequence for calculating sensitivity coefficients and response uncertainties to nuclear systems analyses for criticality safety applications. TSUNAMI uses the Generalized Perturbation Theory (GTP) that performs similarity analysis and consolidates experimental and computational results through data adjustment. The uncertainties, resulting from uncertainties in the basic data, are estimated using energy-dependent cross-section-covariance matrices [9]. The SAMS module is used to determine the sensitivities of calculated value of keff and other system responses to the nuclear data used in the calculations as a function of a nuclide, reaction type, and energy. This sensitivity of keff to the number density is equivalent to the sensitivity of keff to the total cross-section, integrated over energy. Because the total cross-section sensitivity coefficient tests much of the data used to compute all other sensitivity coefficients, it is considered an adequate test for verification. For each sensitivity coefficient examined by direct perturbation, the keff of the system is computed first with the nominal values of the input quantities, and then with a selected nominal input value increased by a certain percentage, and then with the nominal value decreased by the same percentage. The direct perturbation sensitivity coefficient of keff to some input value α is computed as: (1)where α+ and α− represent the increased and decreased values, respectively, of the input quantity α, and kα+ and kα− represent the corresponding values of keff.
(1)where α+ and α− represent the increased and decreased values, respectively, of the input quantity α, and kα+ and kα− represent the corresponding values of keff.
Statistical uncertainties in the computed values of keff are propagated to direct perturbation sensitivity coefficients by standard error propagation techniques as: (2)
(2)
It is important in sensitivity calculations to ensure that the keff value of the forward and adjoint solutions closely agree, and typically, the transport calculation of concern is the adjoint calculation. More details of the GPT methodology are provided in the SAMS manual [10].
SAMPLER is a module for statistical uncertainty analysis of any SCALE sequences. The SAMPLER methodology samples probability density functions (pdf) defined by information in the SCALE multigroup covariance library by XUSA program and produces a random sample for the input computational data vector (CDV) that contains all nuclear cross-sections used in a transport calculation. After making random perturbations in input data, SAMPLER responses uncertainties are computed by statistical analysis of output responses distribution [11].
The perturbed data vector can be used in any SCALE functional module to perform a single forward solution that computes all the desired perturbed responses. The process is repeated for the specified number of random input samples, and the resulting distribution of output responses from SCALE can be analysed with standard statistical analysis tools to obtain the standard deviations and correlation coefficients for all responses. The typical approach is to assume that the generic multigroup (MG) data pdf is a multivariate normal distribution, which is completely defined by the expected values and covariance matrices for the data. An XSUSA statistical sample consists of a full set of perturbed, infinitely dilute MG data for all groups, reactions, and materials. The SCALE generic multigroup covariance data are given as relative values of the infinitely dilute cross-sections, so a random perturbation sample for cross-sections σx,g(∞) corresponds to Δσx,g(∞)/σx,g(∞). XSUSA converts these values to a set of multiplicative perturbation factors Qx,g that are applied to the reference data to obtain the altered values: (3)
(3)
Subsequently, the multiplicative perturbation factors for all data are pre-processed and stored in a data file for subsequent SCALE calculations [12].
To obtain the uncertainty and correlation coefficient, all parameters are randomly perturbed for each calculation, and the uncertainties and correlations are determined. Mathematically, the uncertainty in an individual output parameter k is determined as: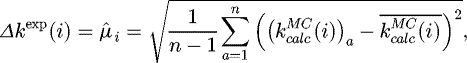 (5)where Δkexp(i) is the uncertainty in system i due to uncertainties in the input parameters.
(5)where Δkexp(i) is the uncertainty in system i due to uncertainties in the input parameters.
 is the ath Monte Carlo (MC) sample of system i, where all uncertain input parameters have been randomly varied within the specified distribution.
is the ath Monte Carlo (MC) sample of system i, where all uncertain input parameters have been randomly varied within the specified distribution.
The covariance between two systems, i and j, is determined as shown in equation (6). (6)
(6)
The correlation coefficient between systems i and j can be determined from equations (5) and (6) as: (7)
(7)
3 Model description
Two main LWR types have been selected for this study, based on previous benchmark experience and available data:
-
Pressurized Water Reactor (PWR) - Three Mile Island 1 (TMI-1);
-
Boiling Water Reactor (BWR) - Peach Bottom 2 (PB-2).
Both models have been analyzed at Hot Full Power (HFP) and Hot Zero Power (HZP) conditions.
Additionally, the two models have been designed with and without control rod.
The different fuel pin cell geometry and reference configuration are schematized in Figures 1 and 2.
SCALE calculations use the Extended Step Characteristic (ESC) approach. The entire problem domain is mapped regarding a set of finite cells. Cells sharing a given side share the value of the angular flux on that side. Once the angular flux has been determined for all sides of the cell for the given direction, it is possible to use a neutron balance to compute the average value of the angular flux within the cell. The process is then repeated for all direction. Numerical quadrature can then be used to determine the average scalar flux in each cell in the problem domain and can be used to determine fission and scattering reaction rates and to update the value of average cell source. In this way, the spatial discretization in SCALE allows to obtain satisfactory results.
The propagation of the cross-sections uncertainties across lattice physics is the main purpose of this exercise. To achieve that, in UAM-Benchmark instructions there are defined two assembly design for the models studied (a PWR and a BWR) [13]. These assemblies are shown in Figures 3 and 4 while Table 1 shows both fuel assemblies data.
As a result of implementing both fuel assemblies in TRITON/NEWT code for transport calculation, the layout outputs for both types of assemblies have been obtained, as shown in Figures 5 and 6.
There are different methodologies used in our calculation of this work. These methods cover the deterministic approach (TRITON/NEWT) and Monte Carlo methodology (TRITON/KENO and SERPENT), as well as the Generalized Perturbation Theory (TSUNAMI) to stochastic sampling techniques (SAMPLER).
 |
Fig. 1 The configuration of PB-2 BWR unit cell. |
 |
Fig. 2 The configuration of TMI-1 PWR unit cell. |
 |
Fig. 3 PB-2 BWR assembly design. |
 |
Fig. 4 TMI-1 PWR assembly design. |
Fuel assembly data for the test cases of Exercises I-2.
 |
Fig. 5 BWR and PWR without control rod 2D assembly. |
 |
Fig. 6 BWR and PWR with control rod 2D assembly. |
4 Results
In this section, the results of transport calculation with TRITON/NEWT, SERPENT-2 and TRITON/KENO are presented, as well as the sensitivity analysis and propagation of uncertainties results that were performed using TSUNAMI and SAMPLER modules. All calculations were carried out for four assemblies models (like shown in Figs. 5 and 6) and two different states (HFP and HZP), with a total of eight configurations for this test case in UAM-Benchmark, Exercise I-2.
4.1 TRITON/NEWT and SERPENT-2 results
Results for the keff and cross-section values are summarized in this section. The aim is to compare TRITON/NEWT and SERPENT-2 results with the average of Benchmark participation values. In the TRITON/NEWT modules, the 238-group nuclear data library collapse was used. Otherwise, the computation with the SERPENT-2.1.22 code was carried out with two libraries, JEFF-3.1 and ENDF/B-VII, to compare results with SCALE (ENDF/B-VII.1 library).
The output values compared in this paper are listed in Table 2. Comparison of TRITON/NEWT and SERPENT-2 are carried out for the multiplication factor (keff), the Absorption cross-section, the Fission cross-section, the Diffusion cross-section and the Flux. All cross-section values are presented for both groups, Fast and Thermal.
In Tables 3 and 4, the first column shows the output values compared in this paper, the second one are the reference values found in UAM-Benchmark results. The third and fourth columns represent TRITON/NEWT calculations and its error with UAM-Benchmark references. Subsequently, the results of SERPENT-2 calculations and their comparison with TRITON/NEWT and UAM-Benchmark values are presented.
The reference values adopted in these tables have been calculated as an average of all submitted results of all benchmark participants, referring to the last submission of 2013.
It should be considered that each participant uses their own code, and this can introduce errors due to the different methodology of each code, but the objective of the benchmark program takes into account these discrepancies.
Therefore, in this work, we calculated the average results of all participants and it is intended to calculate the error between our simulation against SCALE and SERPENT codes.
It is evident from Table 3 that there is good agreement between TRITON/NEWT and reference values, especially for the unrodded configurations. There is a slight recurring discrepancy in the flux value (in both groups, one and two), but it is assumed to be because of different normalization methods of implemented codes in this benchmark exercise.
In Table 3, comparing the SERPENT-2.1.22 results with TRITON/NEWT and UAM-Benchmark, it can be seen a good agreement in both models (BWR and PWR) as has been observed for SCALE results. The slight differences, especially in flux and diffusion coefficient results, can be due to the different methodologies (Monte Carlo) implemented in SERPENT code. In fact, in order to obtain most accurate results, the option B1 was adopted in SERPENT calculation while this option is not available in the SCALE beta version used in this work.
Additionally, we have compared SERPENT calculations using both JEFF-3.1 and ENDF/B-VII libraries, and the JEFF-3.1 results are more close to TRITON/NEWT values despite TRITON/NEWT uses the ENDF/B-VII library.
Even though the slight differences comparing SERPENT with validated and reference results, it could be a good transport calculation code, ongoing testing and validation.
With the aim to show a clearest exposition of the results, the standard deviations in SERPENT, which are lower than 30 pcm for all cases presented, are avoided in Tables 3 and 4.
Table 4 shows good agreement between TRITON/NEWT and reference values like it was presented in Table 3. Comparing SERPENT-2 results with TRITON/NEWT and UAM-Benchmark, the results are similar, as shown in PWR configuration in Table 3.
Even though a different approach is used in the SERPENT code, there is an acceptable agreement between SERPENT-2 and TRITON/NEWT and Benchmark values. In this case, JEFF-3.1 library results are a little bit better comparing with ENDF/B-VII library.
As a conclusion, it is important to give relevance to the short computational times in transport calculation for SERPENT code that was found faster than TRITON/NEWT code. In fact, in SERPENT calculation they have simulated 50,000 particles and 350 cycles in which the first 50 cycles were discarded because of its low statistical weight.
For all exercises, it was used a cluster composed of four blocks with 18 servers equipped with two processors Intel Xeon E5-4620 8c/16T and with a RAM of 64 GB DDR3, and 2 × interfaces 1 0 GbE.
A comparison of the total computational time between SERPENT and TRITON/NEWT calculations, for PWR_HFP_unrodded configuration, returns:
-
SERPENT total computational time (seconds): 935;
-
TRITON/NEWT total computational time (seconds): 1358.
Parameter list to compare - Exercise I-2.
Comparison of cross-section values of PWR Benchmark configuration exercises I-2.
Comparison of cross-section values of BWR Benchmark configuration exercises I-2.
4.2 TRITON/KENO and SERPENT-2 results
From TRITON/KENO calculation, the best estimate system of keff in 3D Monte Carlo methodology is obtained, and it is possible to compare these results with deterministic values as shown in Table 5. In this table, the first column shows TRITON/KENO results, the keff values obtained in TRITON/NEWT figured in the second column, and its error with TRITON/KENO was finally reported.
Analysing Table 5 is possible to corroborate a good agreement through both SCALE models since the largest error calculated has been 0.45%.
Comparison of KENO and NEWT keff assembly results.
4.3 TSUNAMI-2D results
TSUNAMI module is very useful for sensitivity analysis and propagation of uncertainties of cross-sections. TSUNAMI employs the Generalized Perturbation Theory and determines the sensitivities coefficient for each nuclide. Furthermore, the sensitivity coefficients for total reaction for each nuclide and mixture can be calculated with this module.
A list of four major contributors to the uncertainty in keff by individual energy covariance matrices is presented in Figure 7 for BWR calculations and in Figure 8 for PWR calculations.
In both figures, it is possible to find out that the list of major contributors does not vary greatly from case to case, and for all cases uranium seems to be responsible for the uncertainty of keff. In particular, 238Un,γ, 235Unubar, 238Un,n’, are present at the top of contributors list.
Finally, looking at these results is possible to wise up the relative standard deviation due to cross-section covariance data. The relative standard deviation has been close to 0.50% in all cases, for both BWRs and PWRs calculations.
Likewise, it is interesting to analyse the sensitivity profiles of these major contributors, as shown in Figures 9 and 10. The sensitivity per unit lethargy profiles looks similar, with peaks ranging from 0.28 to 0.35. Sensitivity at Hot Full Power state has emerged greater than sensitivity at Hot Zero Power state, for all cases of study. Moreover, sensitivity profile varies only slightly from case to case, and they do not lead to changes in the uncertainty of the keff. Figures 9 and 10 represent BWRs and PWRs calculations, respectively.
 |
Fig. 7 Most important contributor to uncertainty in keff (%Δk/k) in BWRs. |
 |
Fig. 8 Most important contributor to uncertainty in keff (%Δk/k) in PWRs. |
 |
Fig. 9 Sensitivity profiles of most important contributor to uncertainty in keff, BWRs cases. |
 |
Fig. 10 Sensitivity profiles of most important contributor to uncertainty in keff, PWRs cases. |
4.4 SAMPLER results
SAMPLER calculation provides not only estimates for the expected values of the data but also covariance data describing the correlated uncertainty. SAMPLER repeats perturbation steps for a specified number of samples to obtain a distribution of results that can be converted to a standard deviation and correlation coefficients. The SCALE Criticality Safety Analysis Sequence (CSAS) with the 238-group nuclear data library was used for the computations.
Based on the Wilks’ approach [14], the sample size for double tolerance limits with a 95% of uncertainty and with 95% of statistical confidence for the output variables is equal to 146 samples [15], which is the number of runs performed in this work.
To provide information on sampling convergence, layout response of SAMPLER results is presented. For every case run within SAMPLER, any number of responses can be extracted. For instance, the histogram plots that indicate the distribution of the keff and some cross-section computed values for these benchmark exercises are listed below. Figure 11 shows histogram results of BWR with control rod, at hot zero power state (HZP). The keff and two cross-sections (fission and flux) values for the fast and thermal group are represented.
While Figure 12 shows PWR histogram results, in unrodded configuration and at hot full power state (HFP).
In the same way, are represented the keff and fission, and flux cross-section results for the fast and thermal group.
According to the print flag set by the user, SAMPLER also prints a list of tables with interesting information, like average values and standard deviation, correlation matrices, and covariance matrices and so on. Another of interesting results of perturbed variables in SAMPLER layout is the running average, which represent average values and standard deviation for samples of the population during simulation.
Moreover, in SAMPLER response it is possible to see that samples population are closer to the average value and almost entirely within its standard deviation, this is shown in the figures below. According to Wilks’ theory, more than 95% of reliability is reached with 146 samples.
Figure 13 shows samples population with averaged values and standard deviation of BWR with control rod configuration, at hot zero power state (HZP). The keff and two cross-sections (fission and flux) values, for the fast and thermal group, are represented. While Figure 14 shows PWR results of samples population with averaged values and standard deviation, in unrodded configuration and at hot full power state (HFP). In the same way, are represented the keff and fission and flux cross-section results, for the fast and thermal group.
 |
Fig. 11 Histogram plot for keff and two cross-section calculations, for BWR HZP rodded case. |
 |
Fig. 12 Histogram plot for keff and two cross-section calculations, for PWR HFP unrodded case. |
 |
Fig. 13 Samples population for keff and two cross-section calculations (fission and flux), for BWR_HZP with control rod. |
 |
Fig. 14 Samples population for keff and two cross-section calculations (fission and flux), for PWR_HFP without control rod. |
5 Conclusions
This work has been carried out in the framework of UAM-Benchmark Exercise I-1 Cell Physics and I-2 Lattice Physics. The two test cases (PB-2 BWR and TMI-1 PWR) have been analyzed in two different configurations and two different states, with the objective of quantifying the uncertainty in all step calculation and propagate uncertainties in the LWR whole system.
Transport calculations have been analyzed with the deterministic code TRITON/NEWT and stochastic code SERPENT-2.1.22 with the aim of comparing keff and cross-sections results between both codes and with UAM-Benchmark reference values.
Sensitivity calculations have been performed with TSUNAMI module, which uses Generalized Perturbation Theory, and SAMPLER for the perturbed cross-section with stochastic sampling techniques.
The following significant conclusions can be highlighted:
-
TRITON/NEWT is a solid, validated code that has performed well the UAM-Benchmark calculations but spent more computational times comparing against the SERPENT-2 results. Even though the slight differences comparing SERPENT with validated and reference results, this code could be a good transport calculation code, ongoing testing and validation;
-
TSUNAMI module was adopted to estimate sensitivity and uncertainty analysis, the impact of the uncertainties in the basic nuclear data on the calculation of the multiplication factor and microscopic and macroscopic cross-sections. Uncertainties were found to be ≈0.5% on keff. The particular 238Un,γ, 235Unubar, 238Un,n’ were found to be the most important contributors to the uncertainty in these exercises. The deterministic solutions were compared with SAMPLER response, and good agreement was found for this exercise.
Acknowledgments
This work contains findings produced within the OECD/NEA UAM-Benchmark.
This work has been supported by the Generalitat Valenciana under GRISOLIA/2013/A/006 (037) subvention and partially under Project PROMETEOII/008.
References
- K. Ivanov et al., Benchmarks for Uncertainty Analysis in Modelling (UAM) for the design, operation and safety analysis of LWRs (NEA/NSC/DOC, 2012) [Google Scholar]
- SCALE: a comprehensive modelling and simulation suite for nuclear safety analysis and design, ORNL/TM-2005/39, Version 6.1, Oak Ridge National Laboratory, 2011 [Google Scholar]
- M.A. Jessee, M.D. DeHart, TRITON: a multipurpose transport, depletion, and sensitivity and uncertainty analysis module (Oak Ridge National Laboratory, 2011) [Google Scholar]
- M.A. Jessee, M.D. DeHart, NEWT: a new transport algorithm for two-dimensional discrete-ordinate analysis in non-orthogonal geometries (Oak Ridge National Laboratory, 2011) [Google Scholar]
- B.J. Ade, SCALE/TRITON Primer: a primer for light water reactor lattice physics calculations, U.S. NRC Report NUREG/CR-7041, Oak Ridge National Laboratory, 2012 [Google Scholar]
- D.F. Hollenbach, L.M. Petrie et al., KENO-VI: a general quadratic version of the KENO program (Oak Ridge National Laboratory, 2009) [Google Scholar]
- J. Leppänen, SERPENT: a continuous-energy Monte Carlo reactor physics burnup calculation code (VTT Technical Research Centre of Finland, 2013) [Google Scholar]
- M. Aufiero et al., A collision history-based approach to sensitivity/perturbation calculations in the continuous energy Monte Carlo code SERPENT, Ann. Nucl. Energy 85 , 245 (2015) [Google Scholar]
- B.T. Rearden, M.A. Jessee, M.L. Williams, TSUNAMI-1D: control module for one-dimensional cross-section sensitivity and uncertainty (Oak Ridge National Laboratory, 2011) [Google Scholar]
- B.T. Rearden, L.M. Petrie, M.A. Jessee, M.L Williams, SAMS: sensitivity analysis module for SCALE, ORNL/TM-2005/39 Version 6.1, Oak Ridge National Laboratory, 2011 [Google Scholar]
- M.L. Williams et al., SAMPLER: a module for statistical uncertainty analysis with SCALE sequences, Oak Ridge National Laboratory, Draft documentation, 2011 [Google Scholar]
- M.L. Williams et al., A statistical sampling method for uncertainty analysis with SCALE and XUSA, Nucl. Technol. 183 , 515 (2012) [Google Scholar]
- K. Ivanov et al., Benchmarks for Uncertainty Analysis in Modelling (UAM) for the Design, Operation and Safety Analysis of LWRs. Volume I: Specification and Support Data for Neutronics Cases (Phase I) (OECD Nuclear Energy Agency, 2013) [Google Scholar]
- S.S. Wilks, Mathematical statistics (John Wiley & Sons, 1962) [Google Scholar]
- I.S. Hong, D.Y. Oh, I.G. Kim, Generic Application of Wilk's Tolerance Limits Evaluation Approach to Nuclear Safety, in OECD/CSNI Workshop on Best Estimate Methods and Uncertainty Evaluations , 2011 (NEA, CSNI, 2011) [Google Scholar]
Cite this article as: Antonella Labarile, Nicolas Olmo, Rafael Miró, Teresa Barrachina, Gumersindo Verdú, Comparison of SERPENT and SCALE methodology for LWRs transport calculations and additionally uncertainty analysis for cross-section perturbation with SAMPLER module, EPJ Nuclear Sci. Technol. 2, 11 (2016)
All Tables
All Figures
 |
Fig. 1 The configuration of PB-2 BWR unit cell. |
| In the text | |
 |
Fig. 2 The configuration of TMI-1 PWR unit cell. |
| In the text | |
 |
Fig. 3 PB-2 BWR assembly design. |
| In the text | |
 |
Fig. 4 TMI-1 PWR assembly design. |
| In the text | |
 |
Fig. 5 BWR and PWR without control rod 2D assembly. |
| In the text | |
 |
Fig. 6 BWR and PWR with control rod 2D assembly. |
| In the text | |
 |
Fig. 7 Most important contributor to uncertainty in keff (%Δk/k) in BWRs. |
| In the text | |
 |
Fig. 8 Most important contributor to uncertainty in keff (%Δk/k) in PWRs. |
| In the text | |
 |
Fig. 9 Sensitivity profiles of most important contributor to uncertainty in keff, BWRs cases. |
| In the text | |
 |
Fig. 10 Sensitivity profiles of most important contributor to uncertainty in keff, PWRs cases. |
| In the text | |
 |
Fig. 11 Histogram plot for keff and two cross-section calculations, for BWR HZP rodded case. |
| In the text | |
 |
Fig. 12 Histogram plot for keff and two cross-section calculations, for PWR HFP unrodded case. |
| In the text | |
 |
Fig. 13 Samples population for keff and two cross-section calculations (fission and flux), for BWR_HZP with control rod. |
| In the text | |
 |
Fig. 14 Samples population for keff and two cross-section calculations (fission and flux), for PWR_HFP without control rod. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



