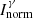EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 10 (2024) EPJ Nuclear Sci. Technol., 10 (2024) 6 Full HTML
Open Access
Issue
EPJ Nuclear Sci. Technol.
Volume 10, 2024
Article Number 6
Number of page(s) 11
DOI https://doi.org/10.1051/epjn/2024007
Published online 18 June 2024

© G. Henning et al., Published by EDP Sciences, 2024

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Motivations

This paper is written by researchers involved in the NACRE project (le Noyaux Au Coeur du RéactEur, Nucleus at the heart of the reactor), founded by the French NEEDS multi-partners and inter-disciplinary framework between the CNRS, CEA, IRSN, ANDRA, EDF, Framatome Orano, and BRGM. NACRE aims to improve evaluated nuclear data for reactor applications by developing new experimental and evaluation techniques and better uncertainty control for cross sections, fission products, and their decay. Within the scope of our respective work, we realized that experimental nuclear data (such as cross sections, fission yields, decay parameters, etc.) typically uses some nuclear structure information (e.g. γ intensity, level existence and their excitation energy, spin, and parity) to interpret experimental measurements (for example, when estimating a cross-section starting from a partial (n,  n′ γ) cross-section – see Sect. 2.4). Additionally, during the evaluation process, the same structure and decay data may also be used as input to modeling codes. In this paper, we differentiate between nuclear data, meaning cross sections (integral or differential), fission fragments yields, decay energy, ... that are often gathered into evaluated databases, and nuclear structure and decay data, i.e. nuclei’s level scheme, lifetime, and decay scheme. Therefore, nuclear structure and decay data have a double impact on evaluation precision: first when interpreting the experimental data that is used in the evaluation process, and second when used as a parameter in the evaluation itself.

All this structure information comes with uncertainty (although, in some cases, the uncertainty may not even be known or quoted). Therefore, the precision of experimentally obtained nuclear data is directly impacted, regardless of how well the measurement is performed.

As the nuclear reactor application studies need an extra level of precision that is not yet reached [1, 2], one needs to lower the uncertainties on structure and decay data, so that it reflects directly on the precision of experimentally derived nuclear data.

The first and most important step regarding this issue is to be careful when interpreting experimental results depending on nuclear structure data, and express them in such a way that they can be easily updated if new structure information is made available. Additionally, the impact of structure uncertainty (such as unknown level spin and parity, high uncertainty on transitions branching ratios) on the derived nuclear data must be studied and quantified (via sensitivity studies), so that improvement on structure data can be planned accordingly.

The NACRE project was instrumental in revealing the shared issue of the limited precision in nuclear structure and decay data for the wider community of nuclear data for reactor applications. The aim of this paper is to stimulate the interest of the nuclear structure and decay measurement community to perform dedicated experiments, and afterward propagate the obtained new structure data into better evaluation.

The following sections present some of these structure data sticking points and the expected improvement from new structure measurements for nuclear data.

2. Case studies

2.1. Fission products yields

Historically, independent fission product yields Y(A, Z), where A is the isotope mass and Z its nuclear charge, are one of the first observables to be measured after the nuclear fission process was discovered [3, 4]. For many years, these quantities were considered a probe of the nuclear fission process and allowed the testing of numerous theoretical hypotheses [5–13]. Fission yields are also mandatory for decay heat calculations [14], spent fuel compositions [15], or prediction of neutron poisons and beta-delayed neutron precursors which permit reactor control for instance. They are involved in more fundamental physics questions such as the so-called “antineutrino reactor anomaly” [16, 17].

For the last decade, the French Alternative Energies and Atomic Energy Commission (CEA), in collaboration with the Institut Laue-Langevin (ILL) and the Laboratory of Subatomic Physics and Cosmology (LPSC) has developed an experimental program for measuring independent fission product yields [18], fission product mass yields [19] and isomeric fission product yields [20] with the LOHENGRIN recoil spectrometer at the ILL. The spectrometer has been in operation since the mid 1970s [21]. It is a combination of a dipole magnet, an electric condenser, and a reverse energy dispersion magnet added in the 1990s [22]. Fission products coming from a fissile target placed near the core of the ILL reactor are selected through these three deflectors according to their ratio A/q and E k /q with A, q, and E k the fission product mass, ionic charge, and kinetic energy respectively. An ionization chamber is generally used to determine the fission product mass. By using High Purity Germanium detectors (HPGe) it is possible to have a clear identification of fission products. Indeed, fission products are mainly radioactive and decay through β− transitions, followed by a specific γ cascade. Then, knowing the nuclide, its nuclear charge Z can be derived.

Since the selection of fission products is made through the ratio A/q and Ek/q, to assess Y(A, Z), all the kinetic energies and ionic charges possible should be measured. However, due to limited beam time, target lifetime, and the spectrometer resolution, such consideration is not realistic. Therefore, a specific data-taking procedure has been developed in order to measure with the best accuracy Y(A, Z). Eight HPGe surround a vacuum chamber with movable tape inside. First, the background of the experimental setup is measured. Next, a beam with the selected A,  q,  Ek triplet is implanted and data are recorded for 20−30 min. Third, implantation is stopped the tape is moved a few meters away, and the procedure is restarted from the first step by measuring the background. This background mainly comes from the decay of fission products implanted directly on the walls of the vacuum chamber instead of the movable tape.

The analysis procedure to go from the γ-rays count rate to the independent fission product yield is complicated and involves additional kinetic energy and ionic charge distribution measurements. Nonetheless, one of the major uncertainties on Y(A, Z) comes from decay data, namely the γ intensity I γ . This quantity is taken in the nuclear databases and can be written as 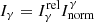where 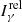is a relative factor which is independent of one γ-ray to another (for the same cascade) and 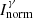a normalization factor which is common for each γ-ray of a single cascade. For instance, 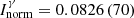for the β− decay of 139I [23]. Figure 1 shows the impact of the latter on the Y(A, Z) for the mass A = 139. We can see how reduced is the uncertainty in the case of 139Cs when a null uncertainty (i.e. no uncertainty) on 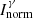is considered. A good knowledge of this quantity is crucial for our measurements. Note that if new values of 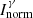are provided, the update of our results can be provided sooner after.

thumbnail Fig. 1.

Absolute independent fission product yields for the mass A = 139 chain and comparison with the JEFF-3.3 database [24]. Left: all the uncertainties are propagated. Right: the uncertainty associated with was set to 0. Correlation matrices (bottom) in both cases are also displayed showing structures reflecting the analysis procedure. The structures reflect the analysis procedure. In this case, the resolution of the Bateman equations and the normalization procedure are in competition. The figure comes from [19].

The impact on the covariance matrix is also noticeable. In such studies, the correlation matrix reflects the underlying analysis procedure. In this specific case of A = 139, each nuclide is fed by its father or directly through the fission process. Therefore, correlations exist only with a nuclide and its father which are related through the Bateman equations. Also, the sign of the correlation is a competition between the resolution of the Bateman equations (positive correlations) and the normalization procedure (negative correlations) (left correlation matrix of Fig. 1). However, if the uncertainty coming from 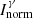is set to 0, all the correlations increase. For instance, we can see that the correlation between 139Xe and 139I is close to 1. It means that the total uncertainty of 139Xe is mainly coming from the total uncertainty of 139I. Indeed, the correlation also reflects the weight of the independent uncertainty (typically the statistical uncertainty or here the 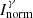term) over the total uncertainty (right correlation matrix of Fig. 1).

The required high precision can be accessed using facilities such as ISOLDE [25]. For instance, the Isolde Decay Station [26] could be used to perform high precision γ spectroscopy by combining HPGe and β detectors. For example, it is possible to select a given radioactive nuclide, such as 137Te. Then, the beam is implanted into a moving tape system, and put in front of the γ and β detectors. The decay of the mass chain A = 137 up to the stable nuclide 137Ba is then recorded and the γ intensities for each nuclide can be extracted with high precision. The absolute values are derived with respect to 137Cs, for which nuclear data are well known. Such an experiment would allow us to improve the knowledge of the nuclear structure data and therefore the precision of the independent fission yields measured with the LOHENGRIN spectrometer.

Up to now, the lowest statistical uncertainty in LOHENGRIN data is about 5%. Therefore, if the uncertainties from the nuclear database are of this order of magnitude, an uncertainty reduced by 3−10% on the fission product independent yield is expected. A recent calculation on the total dose rate and its uncertainty in specific areas of Nuclear Power Plants within accidental conditions [27] have shown the importance of fission product independent yields. Especially, the reduction of the uncertainty is directly related to this latter quantity. For instance, a reduction of uncertainty by a factor of 5 on the independent yield of 136Cs induces a reduction of about 15% in the uncertainty of the total dose rate of 136Cs.

Moreover, it is well known that the variance-covariance matrix of evaluated fission yields has a major impact on nuclear reactor quantities such as the uncertainty of decay heat [28–30]. This is illustrated in Figure 2 where the decay heat uncertainty of a single fuel pin of a UOX fuel at 45 GWd/t is calculated with the JEFF-3.3 database [24] as a reference and by using a new 235U(nth, f) fission yield evaluation [31–33] which produces a coherent variance-covariance matrix. When only the propagation of the variances is accounted for, a global uncertainty reduction of about 0.1%−0.5% can be observed over the whole time range i.e. from 1 s to 9.5 × 109 s (≈300 years). Taking into account the full variance-covariance matrix, the total decay heat uncertainty is reduced down to about 1.5% at 30 years (≈9.5 × 108 s), i.e. in a time range where a limited number of fission products contribute to the decay heat. It has to be noted that the variance-covariance matrix of evaluated fission yields relies on the experimental variance-covariance matrix of measured fission yields. In addition, a stronger reduction is expected if variance-covariance matrix of 239, 241Pu fission yields is used.

thumbnail Fig. 2.

Impact of a new 235U(nth, f) fission yields evaluation on the decay heat uncertainty calculated for a PWR cell UOX at 45 GWd/t. The library of evaluated data used for the calculation is JEFF-3.3 (full bold black line labeled “JEFF-3.3”). The dashed lines correspond to the uncertainty propagation of nuclear data covariances but where the independent fission yields of 235U(nth, f) have been replaced by one of the new evaluations (thin dashed line: only the variances of independent 235U fission yields are propagated in the Decay heat calculation; bold dashed line: the full variance-covariance matrix of the new 235U fission yields evaluation are propagated).

Previous experiments were performed in the heavy mass region [34, 35] due to the lack of data in this region. Nuclides that have been measured with LOHENGRIN and would require improvements are 132, 136Sb, 137Te, 137, 139I, 137, 139, 140, 141Xe, 138m, 139Cs. The central role of the A = 139 mass chain in the absolute normalization process necessitates specific efforts.

2.2. Fission process: de-excitation of fission fragments

An important aspect in the modeling of the fission process is the description of the de-excitation of primary fission fragments by neutron, gamma, and conversion electron emission. This is the aim of Monte Carlo codes such as FREYA [36], CGMF [37], or FIFRELIN [38]. In FIFRELIN, the RIPL-3 database [39, 40] is used at low energy for describing the nuclear level scheme. Unfortunately, fission fragments are neutron-rich nuclei and some of them are poorly known (especially before neutron emission, right after fission). At high energy (from keV to MeV, depending on the nucleus) the level scheme is completed with energy-, spin- and parity-dependent level density models. De-excitation is performed through a Hauser-Feshbach algorithm using photon strength functions, neutron transmission coefficients, and internal conversion coefficients. Details can be found in the literature [38, 41] and references therein. Table 1 is an example of such nuclei. Good knowledge of the level scheme for gamma and electron de-excitation is mandatory for the low mass range of those neutron-rich nuclei (low mass isotopes). For very neutron-rich nuclei (isotopes with higher masses), the de-excitation proceeds by neutron emission, and then another ingredient is even more sensitive to the details of the level scheme: the neutron transmission coefficient calculated from an optical potential parametrization specifically dedicated to deformed neutron-rich nuclei.

Table 1.

List of potential primary fission fragments having an incomplete level scheme and yield higher than 0.5% in thermal fission of 235U.

Improved knowledge of the nuclear level scheme has already allowed us to better infer the reliability of nuclear model parameters used in the de-excitation process [42, 43]. As an example, recent improvements have been obtained for neutron-rich krypton isotopes 90 − 95Kr located in the low Z boundary of the A ≈ 100 region and odd-mass neutron-rich bromine isotopes 87 − 93Br [44]. Finally, even a simple spin assignment can be an important upgrade because if only the energy position of a given level is known, the spin/parity has to be sampled from a spin distribution accounting for a spin cut-off parameter, which is an additional model parameter.

2.3. Decay data

Nuclear decay data plays a crucial role in the field of nuclear engineering, as it provides detailed information about the properties of different isotopes. Indeed, fission products in a reactor generate huge quantities of secondary particles like alpha particles, beta electrons, antineutrinos, and gamma rays. A detailed budget of these emissions is used to predict the behavior of fuel in a reactor, as well as to understand the reactions that take place within. Nuclear decay data can also be used to determine the rate of fuel burnup and to identify the specific isotopes that are present in the reactor at any given time. Additionally, decay data is used in the design of radiation shielding and the prediction of the long-term behavior of nuclear waste.

Accurate and reliable nuclear decay data are thus essential for the reactor community, but also in fundamental physics, radiotherapy and dosimetry, radionuclide metrology, or radioprotection studies. For each isotope, nuclear structure information has to be established at the best of knowledge at the moment of the evaluation: decay scheme and branching ratios; total and partial half-lives; level spins, parities, half-lives, and energies; transition types; emission processes and their intensities; mean and total decay energies; and atomic radiations. Each recommended quantity must be associated with an uncertainty, carefully determined.

Taking into account all the available literature, evaluators have to deal with a wide variety of physical processes and experimental techniques. Ultimately, the quality of the recommended decay data is highly correlated to the accuracy and reliability of the published measurements of nuclear structure data. However, some of the recommended quantities must be taken from theory when no experimental data is available. Nuclear decay data would thus also benefit from improved theoretical predictions of nuclear structure.

The recommended data from the Decay Data Evaluation Project (DDEP) [45] were incorporated into the current version (3.3) of the Joint Evaluated Fission and Fusion (JEFF) file project of the OECD Nuclear Energy Agency [46]. The evaluators are in demand of users’ feedback on the recommended decay data. In the past, evaluations of the decays from 148g, m Pm, two important reactor poisons [47], and from four radioactive xenon isotopes (131m, 133, 133m, 135Xe) used in nuclear explosion monitoring [48] were driven by users’ needs. A priority list of isotopes that are the most critical to evaluate would be very valuable. Regarding fuel cycle applications, a priority list of radionuclides whose nuclear data needs improvements is proposed in Table 2. A detailed comparison between international libraries of the nuclear data of the most important nuclides involved in decay heat between 1 year and 100 years of cooling is also proposed in [49] (for other listings, see [50, 51]).

Table 2.

List of important isotopes for fuel cycle applications and that would benefit from a re-evaluation of their decay data.

Recently, 239Np decay, an important isotope in the decay heat process, has been identified for re-evaluation [52]. The latest DDEP evaluation was completed in 2006 with 14 beta transitions and 39 gamma transitions [53], and new measurements have been published since then that could significantly influence the decay scheme. Similarly, 129m Sn decay would need to be re-evaluated. This isotope is the main precursor of 129I, which is the most important isotope in gaseous discharges from nuclear fuel reprocessing plants. The decay of 129m Sn has not been evaluated yet by DDEP and in the 2014 ENSDF (Evaluated Nuclear Structure Data File) evaluation, the procedure that established the 47 beta transitions and the 97 gamma transitions is poorly documented. A new analysis of the available literature would allow the recommendation of specific measurements for the most critical quantities in establishing the decay scheme.

Both mean values and uncertainties, well established and controlled, are needed to ensure the right level of safety margins. Nuclear data uncertainties are propagated through depletion calculations, and the quality and accuracy of the results depend on the completeness and quality of the nuclear data covariances (variances and correlations between nuclear data) [54]. By doing so, sensitivity profiles of quantities of interest to nuclear data are also established. Those sensitivity profiles are useful to provide feedback to the evaluators or to identify nuclear data to improve. Sensitivity profiles may be established by direct perturbation of the nuclear data in the input nuclear data libraries [55] or by perturbation theory [56].

Until recently, the main contributors to the global uncertainty budget were the independent fission yield uncertainties due to the lack of covariance matrix taking into account experimental correlations, models, and physical constraints. For the next JEFF database release, complete covariance matrices will be provided at least for 235U(nth, f) and 239Pu(nth, f) fission yields. Therefore, the variance that arises from decay data will increase proportionally in the global uncertainty budget.

thumbnail Fig. 3.

Impact of the new JEFF-3.3 decay data and fission yield library on the Dickens fission burst experiment (gamma heat on the left, total heat on the right).

In the near future, the decay data evaluators will have to face a difficult challenge in integrating the measurements of beta and gamma decays using the Total Absorption Gamma-ray Spectroscopy (TAGS) technique. Some decay schemes are known to be affected by the Pandemonium effect that comes from the use of Germanium detectors. The low intrinsic and geometrical detection efficiency of this technique is not adapted to high-energy Q-value nuclei with high-density level schemes: the probability of detecting high-energy gammas or the total gamma cascade from high-energy excited levels of the daughter nucleus is very low. This leads to an underestimation of the total gamma energy with an overestimation of β transition intensities of the low-lying energy levels of the daughter isotopes [57]. The TAGS technique is complementary to high-resolution spectroscopy and allows the establishment of Pandemonium-free decay schemes thanks to a very high detection efficiency for the emitted gamma rays [58]. This technique has proven its ability to measure β-intensity from high excitation energy states even in the case of beta-delayed neutron emitters where the measurements showed a gamma/neutrons emission competition above the neutron emission threshold [59]. The main constraint of this technique is the limited energy resolution of the scintillation crystals. The (NA)2STARS Project [60] is an upgrade of present TAGS detectors with LaBr3 crystals. This will allow us to associate a better energy resolution to the present high detection efficiency with a very good time resolution which will allow for gamma/neutron discrimination. This second-generation TAGS detector will be capable of measuring the beta decay properties of even more exotic nuclei.

In the latest JEFF-3.3 library, the mean beta and gamma decay energies of nine isotopes (104, 105, 106, 107Tc, 87, 88Br, 92, 94Rb and 105Mo) resulting from the analysis of TAGS experiments and a re-evaluation of their decay schemes [61–63] was also added. The decay data of these isotopes were identified as possibly suffering from the Pandemonium effect. The new values differ from 10 to 40% with the previous JEFF-3.1.1 data and their uncertainties were strongly reduced.

As an example, the JEFF-3.3 library was tested on elementary fission burst experiments of 239Pu in a thermal spectrum. Those experiments consist of irradiating a sample of a given fissile isotope with a neutron flux and measuring the decay power emitted by fission products following the irradiation. Calculations were performed with the DARWIN2.3 package [64], as illustrated in Figure 3 and compared to Dickens measurements [65]. The analysis of the results emphasized a clear improvement of the gamma heat following fission of 239Pu between 10 and 5000 s thanks to new TAGS data. Calculation-to-measurement discrepancies on the gamma contribution in this time range are comprised between [−15%; 5%] with JEFF-3.1.1 and between [−5%; −1%] with JEFF-3.3, given that the experimental uncertainty is about 3% at one standard deviation.

More interesting for the fuel cycle is the comparison of fission burst experiments with long irradiation times, which are more similar to real spent fuel. This is illustrated by Figure 4 on the Friesenhahn experiment [66] which consists of the measurement of the beta, gamma, and total heat following a one-day irradiation of a sample of almost pure 239Pu in a thermal neutron flux. The results also show a better agreement to the experimental data with the JEFF-3.3 library, both on gamma and total heats.

thumbnail Fig. 4.

Performances of the JEFF-3.1.1 and JEFF-3.3 libraries on Friesenhahn fission burst experiment (irradiation time = 1 d).

Three sets of decay heat calculations of the Light Particle (ELP) and Electromagnetic (EEM) components both for 235U and 239Pu thermal fission pulses were performed using the Serpent code [67] to estimate the impact of the TAGS measurements [68]. The results are given in Figures 5 and 6. Calculations were compared to decay heat measurements on neutron pulse irradiations for single actinide targets (Dickens and Lowell) and Tobias evaluated data available in the IAEA CoNDERC database [65, 69–72]. The first calculation is based on the JEFF-3.1.1 fission yields and decay sub-libraries where some TAGS data from Greenwood et al. are included for the following nuclei: 90, 90m, 91Rb, 95Sr, 139, 141Cs, 143, 144, 145Ba, 142, 143, 144, 145La, 148Ce, 147, 148, 148m, 149, 151Pr, 153, 154, 155Nd, 152, 153, 154, 156, 157, 158Pm [73, 74].

thumbnail Fig. 5.

235U thermal fission decay heat as a function of cooling time obtained with the JEFF-3.1.1 and JEFF-3.3 libraries with the addition of TAGS data [58, 75–77]. Experimental was taken from the CoNDERC IAEA database [69].
thumbnail Fig. 6.

239Pu thermal fission decay heat as a function of cooling time obtained with the JEFF-3.1.1 and JEFF-3.3 libraries with the addition of TAGS data [58, 75–77]. Experimental was taken from the CoNDERC IAEA database [69].

A second calculation was performed with the latest release of the JEFF library, i.e. the JEFF-3.3, both for the fission yields and decay sub-libraries. The JEFF-3.3 decay sub-library includes some TAGS measurements performed at the University of Jyväskylä per the Valencia-Surrey-Subatech team for the following fission products: 87, 88Br, 92, 94Rb, 105Mo, 104, 105, 106, 107Tc [59, 78–80]. The inclusion of these 9 nuclei where the ELP and EEM decay energies were replaced by the mean beta and gamma decay energies obtained thanks to the TAGS technique improves both the ELP and EEM components for 239Pu thermal burst in the 10−5000 s cooling range. In the last calculation (JEFF-3.3 + TAGS2023), all TAGS data published till January 2023 were added to the JEFF 3.3 decay sub-library taking the remaining TAGS data listed in Table 3 of Algora et al. [58] for the following nuclei: 86Br, 91, 95Rb, 100, 100m, 101, 102, 102m Nb, 137I, 102Tc and 96m Y from Guadilla et al. [75] plus 89, 90Kr, 89, 90, 90Rb, 96Y, 137, 139Xe and 142Cs from the ORNL-Warsaw Collaboration [76, 77]. The electromagnetic decay heat component of 235U thermal fission from 2 to 100 s cooling times is underestimated per the JEFF-3.3 and JEFF-3.3 + TAGS 2023 calculations. At cooling times above 400 s, it is rather difficult to conclude because the three sets of measurements exhibits discrepancies. The differences between the experimental sets of the electromagnetic component of decay heat for 235U thermal fission in the cooling range 300−4000 s remain unresolved to date and extra investigation will require new better quality integral measurements. The inclusion of all TAGS measurements (JEFF 3.3 + TAGS2023) leads to an underestimation of the ELP decay heat component for 239Pu thermal fission in the 10−1000 s cooling range. The ELP decay heat component of 235U thermal fission exhibits some improvement in the 10−200 s cooling range but leads to an underestimation of the 400−2000 s cooling times.

These results show the need for additional TAGS measurements of the remaining high-priority fission product lists established per NEA and IAEA [81].

2.4. Inelastic scaterring cross section measurements

The group at CNRS-IPHC has been measuring (n,  n′ γ) cross sections using prompt γ-ray spectroscopy and neutron energy determination by time-of-flight for many years, and producing exclusive cross-section data [82–84] for numerous isotopes.

From the exclusive (n,  n′ γ) cross sections, there are two methods to infer the total (n,  n′) one. One may directly use level structure information to compute, by adding together weighted σ(n,  n′ γ) (the coefficients being driven entirely by the level scheme structure), the total σ(n,  n′) (or at least a lower or upper bound). Another method, is to use the exclusive (n,  n′ γ) data to constrain the model in order to calculate accurately the total (n,  n′) cross section. However, the calculation codes (TALYS [85, 86], EMPIRE [87], CoH3 [88, 89]) use nuclear structure information (level scheme, including level spins, parities, and lifetimes, as well as transition intensities and multipolarities) as input to their computations. Therefore, any bias or uncertainty in nuclear structure limits the relevance of comparison between theoretical predictions and experimental values.

We identified several limitations in the current databases for nuclei of interest for the nuclear cycle. In 238U, of the 79 γ transitions listed in ENSDF [90], 76% have branching ratios (BR) information, and only 56% are mentioned with uncertainty. A study of the sensitivity of cross section to branching ratios has been carried out using a random variation method (i.e. Monte Carlo) on 238U [82, 83, 91]. This study showed that for some γ rays, a strong sensitivity exists to the branching ratio of other transitions. Branching ratio sensitivity is linked to the level structure of the nucleus. However, when it concerns transitions for which the intensities have large uncertainties, or in the worst case, no tabulated value, the impact on calculated cross section, which are compared to experimental results, can be significant [91]. For example, the 4+ level at 1056.38 keV in the level scheme of 238U in ENSDF [92] is listed without uncertainty on the BR of the decaying transitions. The calculated cross section for the transitions between the third and second excited states (6+ at 307.18 keV to 4+ at 148.38 keV) shows a sensitivity of about 0.4% in calculated σ per % variation around the reference BR to the transitions decaying from this 1056.38 keV–4+ level. As the average uncertainty on BR in the 238U level scheme is around 10%, we can expect about 4% uncertainty on the 6+ to 4+ transitions cross section, which is too high in respect to the < 2% target.

In the same way, the analysis of 232Th(n,  n′ γ) experimental data [93] identified at least 8 transitions that were missing from the ENSDF database. Some were hinted by Demidov et al. [94] but not included yet in the evaluated level scheme. Additionally, some intensities are not known (absent from databases, left at zero in TALYS input files). The case of the 4+ state at 873.0 keV is a good example: the adopted level and γ information lists two γ rays decaying from this state, only one of which has an intensity given (100, without uncertainty), the other (going to the first excited state) has no listed intensity (in TALYS input file, its BR is set to zero). However, in our measurement, we have observed three transitions decaying from this state, and their relative intensities showed that the most intense transition is the one set to 0 in the databases [93].

Finally, for the isotopes 233U and 232U, we similarly found transitions with no relative intensity in the database (from the 691.42 keV 0+ state in 232U, or the 155.2 keV 11/2+ state in 233U – intensities are evenly split between the transitions in TALYS input files). For 233U, the 51.5 keV γ ray from the 9/2+ state at 92.2 keV has its intensity quoted as ≈21 against 100 for the competing γ ray at 92.2 keV to the ground state. However, in the TALYS input file, the intensities listed are 100 for the 92.2 keV transition and 87 for the 51.5 keV one, raising the question of the origin of the deviation from the reference database.

These examples reflect a more general situation and similar problems exist for 239Pu and other actinides. The knowledge of a level scheme is often partial when considering a nucleus of interest for reactors, if not lacking essential information. The consequence is a limited ability to study and infer inelastic neutrons scaterring with a high precision, γ rays intensities being one of the blocking elements in improving of the reaction knowledge. There is therefore a need for new spectroscopic work to increase the knowledge of the nuclei level schemes, in order to infer the total (n,  n′) cross section from exclusive (n,  n′ γ) values.

3. Perspectives

As presented in this paper, nuclear structure information (BR, levels characteristics, ...) is key for the interpretation of many experimental data and their exploitation. The evaluation processes also rely on structure and decay data to produce the evaluated nuclear data. The remaining uncertainties on these structure data limit the accuracy of evaluations and application calculations, regardless of how precise the measurements are performed. Depending on the quantities or applications, some lists (of significant lengths) can be drawn of needed improvements in nuclear structure data.

Our working group discussed this topic during a dedicated workshop [95] that gathered members from the nuclear data and nuclear structure communities. It is our hope that this paper will prompt new measurements on nuclear structure of interest and better support from the funding agencies to the evaluation work that makes the databases alive and useful.

We first notice that structure information for nuclei of interest can often be extracted from many nuclear physics experiments, even when it is not the primary goal of the experiment. For example, a beam impinging on a target material could produce γ rays from scattering reactions that could be analyzed for structure information. In these cases, the structure aspect is often not pursued, and the raw data may be put away once the primary analysis is done, never looked at further. These existing, but un-analyzed and often un-catalogued data sets, have value. With a registry of such data sets, as well as an open data policy, we could put effort in getting updated structure information from these measurements, instead of requiring beam time to perform dedicated measurements in order to get data that already exists. As an example of such case, the data from the first ν-Ball campaign [96] that occurred in 2017–2018 has been identified in 2021 as a possible source of new structure information on 238U, offering answers to the questions raised in Section 2.4 regarding (n,  n′ γ) cross sections [97].

Furthermore, it is noteworthy that once the nuclear structure data is obtained in an experiment, it has to be taken into account in a re-evaluation process in order to be valuable for improving information in the databases. This evaluation work takes time, and the longstanding deficit of manpower dedicated to this subject has become critical for future studies on nuclear reactors. While updating tables may not seem to be a high-impact achievement for funding agencies, we want to stress the upmost importance of updating and maintaining evaluated databases for the general community. It is a very valuable service for the entire nuclear physics field and should not be overlooked.

Acknowledgments

The authors thank Jon Wilson (IJC-Lab) for his help in writing this article.

Funding

This work was supported by the CNRS multipartner NEEDS program.

Conflicts of interest

The authors declare that they have no competing interests to report.

Data availability statement

This article has no associated data.

Author contribution statement

All the authors contributed equally to the writing and pre-publication review of the paper. Greg Henning coordinated the work.

References

  1. G. Aliberti, G. Palmiotti, M. Salvatores, T. Kim, T. Taiwo, M. Anitescu, I. Kodeli, E. Sartori, J. Bosq, J. Tommasi, Ann. Nucl. Energy 33, 700 (2006) [CrossRef] [Google Scholar]
  2. NEA, R. Jacqmin, M. Salvatores, IAE Agency, ONE Agency, Uncertainty and Target Accuracy Assessment for Innovative Systems Using Recent Covariance Data Evaluations: A Report by the Working Party on International Evaluation Co-operation of the NEA Nuclear Science Committee (NEA/OECD, 2008), https://books.google.fr/books?id=rHg0QwAACAAJ [Google Scholar]
  3. O. Hahn, F. Strassmann, Naturwissenschaften 27, 11 (1939) [CrossRef] [Google Scholar]
  4. L. Meitner, O.R. Frisch, Nature 143, 239 (1939) [CrossRef] [Google Scholar]
  5. P. Fong, Phys. Rev. 102, 434 (1956) [CrossRef] [Google Scholar]
  6. B.D. Wilkins, E.P. Steinberg, R.R. Chasman, Phys. Rev. C 14, 1832 (1976) [CrossRef] [Google Scholar]
  7. J.F. Lemaitre, S. Goriely, S. Hilaire, J.L. Sida, Phys. Rev. C 99, 034612 (2019) [CrossRef] [Google Scholar]
  8. Y. Aritomo, S. Chiba, F. Ivanyuk, Phys. Rev. C 90, 054609 (2014) [CrossRef] [Google Scholar]
  9. M.D. Usang, F.A. Ivanyuk, C. Ishizuka, S. Chiba, Sci. Rep. 9, 1 (2019) [Google Scholar]
  10. J. Randrup, P. Möller, Phys. Rev. Lett. 106, 132503 (2011) [CrossRef] [PubMed] [Google Scholar]
  11. K. H. Schmidt, B. Jurado, C. Amouroux, C. Schmitt, Nucl. Data Sheets 131, 107 (2016) [CrossRef] [Google Scholar]
  12. H. Goutte, J.F. Berger, P. Casoli, D. Gogny, Phys. Rev. C 71, 24316 (2005) [CrossRef] [Google Scholar]
  13. D. Regnier, N. Dubray, N. Schunck, Phys. Rev. C 99, 024611 (2019) [CrossRef] [Google Scholar]
  14. A. Tsilanizara, T. Huynh, Ann. Nucl. Energy 164, 108579 (2021) [CrossRef] [Google Scholar]
  15. O. Leray, D. Rochman, P. Grimm, H. Ferroukhi, A. Vasiliev, M. Hursin, G. Perret, A. Pautz, Ann. Nucl. Energy 94, 603 (2016) [CrossRef] [Google Scholar]
  16. G. Mention, M. Fechner, T. Lasserre, T.A. Mueller, D. Lhuillier, M. Cribier, A. Letourneau, Phys. Rev. D 83, 073006 (2011) [CrossRef] [Google Scholar]
  17. A. A. Sonzogni, E.A. McCutchan, T.D. Johnson, P. Dimitriou, Phys. Rev. Lett. 116, 132502 (2016) [CrossRef] [Google Scholar]
  18. A. Chebboubi, G. Kessedjian, O. Serot, H. Faust, U. Köster, O. Litaize, C. Sage, A. Blanc, D. Bernard, A. Letourneau, T. Materna, O. Méplan, P. Mutti, M. Rapala, M. Ramdhane, Eur. Phys. J. A 57, 335 (2021) [CrossRef] [Google Scholar]
  19. S. Julien-Laferrière, A. Chebboubi, G. Kessedjian, O. Serot, O. Litaize, A. Blanc, U. Köster, O. Méplan, M. Ramdhane, C. Sage, Phys. Rev. C 102, 034602 (2020) [CrossRef] [Google Scholar]
  20. A. Chebboubi, G. Kessedjian, O. Litaize, O. Serot, H. Faust, D. Bernard, A. Blanc, U. Köster, O. Méplan, P. Mutti, C. Sage, Phys. Lett. B 775, 190 (2017) [CrossRef] [Google Scholar]
  21. P. Armbruster, M. Asghar, J. Bocquet, R. Decker, H. Ewald, J. Greif, E. Moll, B. Pfeiffer, H. Schrader, F. Schussler, G. Siegert, H. Wollnik, Nucl. Instrum. Meth. 139, 213 (1976) [Google Scholar]
  22. G. Fioni, H.R. Faust, M. Gross, M. Hesse, P. Armbruster, F. Gönnenwein, G. Münzenberg, Nucl. Instrum. Meth. A 332, 175 (1993) [Google Scholar]
  23. P. K. Joshi, B. Singh, S. Singh, A.K. Jain, Nucl. Data Sheets 138, 1 (2016) [Google Scholar]
  24. A.J.M. Plompen, O. Cabellos, C.D.S. Jean, M. Fleming, A. Algora, M. Angelone, P. Archier, E. Bauge, O. Bersillon, A. Blokhin, F. Cantargi, A. Chebboubi, C. Diez, H. Duarte, E. Dupont, J. Dyrda, B. Erasmus, L. Fiorito, U. Fischer, D. Flammini, D. Foligno, M.R. Gilbert, J.R. Granada, W. Haeck, F.J. Hambsch, P. Helgesson, S. Hilaire, I. Hill, M. Hursin, R. Ichou, R. Jacqmin, B. Jansky, C. Jouanne, M.A. Kellett, D.H. Kim, H.I. Kim, I. Kodeli, A.J. Koning, A.Y. Konobeyev, S. Kopecky, B. Kos, A. Krása, L.C. Leal, N. Leclaire, P. Leconte, Y.O. Lee, H. Leeb, O. Litaize, M. Majerle, J.I. Márquez Damián, F. Michel-Sendis, R.W. Mills, B. Morillon, G. Noguère, M. Pecchia, S. Pelloni, P. Pereslavtsev, R.J. Perry, D. Rochman, A. Röhrmoser, P. Romain, P. Romojaro, D. Roubtsov, P. Sauvan, P. Schillebeeckx, K.H. Schmidt, O. Serot, S. Simakov, I. Sirakov, H. Sjöstrand, A. Stankovskiy, J.C. Sublet, P. Tamagno, A. Trkov, S. van der Marck, F. Álvarez Velarde, R. Villari, T.C. Ware, K. Yokoyama, G. Žerovnik, Eur. Phys. J. A 56, 181 (2020) [CrossRef] [Google Scholar]
  25. E. Kugler, Hyperfine Interactions 129, 23 (2000) [CrossRef] [Google Scholar]
  26. R. Licà, H. Mach, L.M. Fraile, A. Gargano, M.J.G. Borge, N. Mărginean, C.O. Sotty, V. Vedia, A.N. Andreyev, G. Benzoni, P. Bomans, R. Borcea, L. Coraggio, C. Costache, H. De Witte, F. Flavigny, H. Fynbo, L.P. Gaffney, P.T. Greenlees, L.J. Harkness-Brennan, M. Huyse, P. Ibáñez, D.S. Judson, J. Konki, A. Korgul, T. Kröll, J. Kurcewicz, S. Lalkovski, I. Lazarus, M.V. Lund, M. Madurga, R. Mărginean, I. Marroquín, C. Mihai, R.E. Mihai, A.I. Morales, E. Nácher, A. Negret, R.D. Page, J. Pakarinen, S. Pascu, V. Paziy, A. Perea, M. Pérez-Liva, E. Picado, V. Pucknell, E. Rapisarda, P. Rahkila, F. Rotaru, J.A. Swartz, O. Tengblad, P. Van Duppen, M. Vidal, R. Wadsworth, W.B. Walters, N. Warr, Phys. Rev. C 93, 044303 (2016) [CrossRef] [Google Scholar]
  27. A. Chebboubi, D. Bernard, V. Vallet, G. Kessedjian, O. Méplan, Y.H. Kim, U. Köster, C. Géhin, F. Sage, M. Ramdhane, M. Houdouin-Quenault, C.E. Düllmann, C. Mokry, J. Runke, D. Renisch, O. Litaize, O. Serot, EPJ Web Conf. 284, 08004 (2023) [Google Scholar]
  28. N. Terranova, O. Serot, P. Archier, C. De Saint Jean, M. Sumini, Ann. Nucl. Energy 109, 469 (2017) [CrossRef] [Google Scholar]
  29. D. Rochman, O. Leray, A. Vasiliev, H. Ferroukhi, A. Koning, M. Fleming, J. Sublet, Ann. Nucl. Energy 95, 125 (2016) [CrossRef] [Google Scholar]
  30. L. Fiorito, C. Diez, O. Cabellos, A. Stankovskiy, G. Van den Eynde, P. Labeau, Ann. Nucl. Energy 69, 331 (2014) [CrossRef] [Google Scholar]
  31. G. Kessedjian, S.M. Cheikh, O. Serot, A. Chebboubi, D. Bernard, V. Vallet, R. Mills, L. Capponi, EPJ Web Conf. 281, 00022 (2023) [Google Scholar]
  32. S.M. Cheikh, G. Kessedjian, O. Serot, A. Chebboubi, O. Litaize, EPJ Web Conf. 281, 00023 (2023) [Google Scholar]
  33. G. Kessedjian, S.M. Cheikh, A. Chebboubi, O. Serot, EPJ Web Conf. 242, 05001 (2020) [CrossRef] [EDP Sciences] [Google Scholar]
  34. F. Martin, Etude des distributions en masse, charge nucléaire et énergie cinétique des produits de fission de l'233U(nth,f) et du 241Pu(nth,f) mesurées auprès du spectromètre de masse Lohengrin (ILL). Theses, Universitéde Grenoble, 2013, https://theses.hal.science/tel-01288258 [Google Scholar]
  35. S. Julien-Laferrière, Approche expérimentale et phénoménolo-gique des rendements de la fission induite par neutron thermique du 239Pu et du 241Pu. Theses, UniversitéGrenoble Alpes, 2018, https://theses.hal.science/tel-01995046 [Google Scholar]
  36. J. Randrup, R. Vogt, Phys. Rev. C 80, 024601 (2009) [Google Scholar]
  37. P. Talou, I. Stetcu, P. Jaffke, M. Rising, A. Lovell, T. Kawano, Comput. Phys. Commun. 269, 108087 (2021) [CrossRef] [Google Scholar]
  38. O. Litaize, O. Serot, L. Berge, Eur. Phys. J. A 51, 177 (2015) [CrossRef] [Google Scholar]
  39. R. Capote, M. Herman, P. Oblozinsky, P. Young, S. Goriely, T. Belgya, A. Ignatyuk, A. Koning, S. Hilaire, V. Plujko, M. Avrigeanu, O. Bersillon, M. Chadwick, T. Fukahori, Z. Ge, Y. Han, S. Kailas, J. Kopecky, V. Maslov, G. Reffo, M. Sin, E. Soukhovitskii, P. Talou, Nucl. Data Sheets 110, 3107 (2009) [NASA ADS] [CrossRef] [Google Scholar]
  40. M. Verpelli, R. Capote, International Nuclear Data Committee INDC(NDS)-0702 (2015) [Google Scholar]
  41. O. Litaize, O. Serot, Phys. Rev. C 82, 054616 (2010) [CrossRef] [Google Scholar]
  42. O. Litaize, A. Chebboubi, O. Serot, L. Thulliez, T. Materna, M. Rapala, EPJ Nuclear Sci. Technol. 4, 28 (2018) [Google Scholar]
  43. T. Materna, M. Rapal, A. Letourneau, A. Marchix, O. Litaize, O. Sérot, W. Urban, A. Blanc, M. Jentschel, U. Köster, P. Mutti, T. Soldner, G. Simpson, C.A. Ur, G. de France, EPJ Web Conf. 146, 04041 (2017) [Google Scholar]
  44. D. Reygadas, Ph.D. thesis, UniversitéGrenoble Alpes, 2021 [Google Scholar]
  45. M.A. Kellett, O. Bersillon, EPJ Web Conf. 146, 02009 (2017) [Google Scholar]
  46. A. Koning, E. Bauge, C. Dean, E. Dupont, U. Fischer, R. Forrest, R. Jacqmin, H. Leeb, M. Kellett, R. Mills, et al., J. Korean Phys. Soc. 59, 1057 (2011) [CrossRef] [Google Scholar]
  47. M. Kellett, M.M. Bé, Appl. Radiat. Isot. 87, 95 (2014) [CrossRef] [Google Scholar]
  48. M. Galan, M. Kalinowski, A. Gheddou, K. Yamba, J. Environ. Radioact. 192, 628 (2018) [CrossRef] [Google Scholar]
  49. H.R. Doran, A.J. Cresswell, D.C.W. Sanderson, G. Falcone, Eur. Phys. J. Plus 137, 665 (2022) [CrossRef] [Google Scholar]
  50. M. Gupta, M. Kellett, A. Nichols, O. Bersillon, Decay Heat Calculations: Assessment of Fission Product. Decay Data Requirements for Th/U Fuel. Tech. rep. (International Atomic Energy Agency, 2010) [Google Scholar]
  51. P. Dimitriou, A.L. Nichols, Total Absorption Gamma-ray Spectroscopy for Decay Heat Calculations and Other Applications. Summary Report of Consultants' Meeting. Tech. rep. (International Atomic Energy Agency, 2015) [Google Scholar]
  52. V. Vallet, D. Bernard, https://www.oecd-nea.org/dbdata/jeff/jeffdoc.html, 2021 [Google Scholar]
  53. M.M. Bé, V. Chisté, C. Dulieu, E. Browne, V. Chechev, N. Kuzmenko, F. Kondev, A. Luca, M. Galán, A. Pearce, X. Huang, Table of Radionuclides, Monographie BIPM-5, Vol. 4 (Bureau International des Poids et Mesures, Pavillon de Breteuil, 92310 Sèvres, France, 2008), http://www.bipm.org/utils/common/pdf/monographieRI/ Monographie_BIPM-5_Tables_Vol4.pdf [Google Scholar]
  54. J. Huyghe, V. Vallet, D. Lecarpentier, C. Reynard-Carette, C. Vaglio-Gaudard, EPJ Nuclear Sci. Technol 5, 8 (2019) [CrossRef] [EDP Sciences] [Google Scholar]
  55. V. Vallet, BEPU (Lucca, France, 2018) https://cea.hal.science/cea-02339070 [Google Scholar]
  56. N. Linden, A. Tsilanizara, J. Tommasi, Ann. Nucl. Energy 185, 109743 (2023) [CrossRef] [Google Scholar]
  57. J. Hardy, L. Carraz, B. Jonson, P. Hansen, Phys. Lett. B 71, 307 (1977) [CrossRef] [Google Scholar]
  58. A. Algora, J.L. Tain, B. Rubio, M. Fallot, W. Gelletly, Eur. Phys. J. A 57, 85 (2021) [CrossRef] [Google Scholar]
  59. E. Valencia, J.L. Taín, A. Algora, J. Agramunt, E. Estévez, M.D. Jordan, B. Rubio, S. Rice, P. Regan, W. Gelletly, Zs. Podolyák, M. Bowry, P. Mason, G.F. Farrelly, A.-A. Zakari-Issoufou, M. Fallot, A. Porta, V.M. Bui, J. Rissanen, T. Eronen, I. Moore, H. Penttilä, J. Äystö, V.-V. Elomaa, J. Hakala, A. Jokinen, V.S. Kolhinen, M. Reponen, V. Sonnenschein, D. Cano-Ott, A.R. Garcia, T. Martínez, E. Mendoza, R. Caballero-Folch, B. Gómez-Hornillos, V. Gorlichev, F.G. Kondev, A.A. Sonzogni, L. Batist, Phys. Rev. C 95, 024320 (2017) [CrossRef] [Google Scholar]
  60. Na2Stars Presentation and Proposal at the Ganil Scientific Council (2023) [Google Scholar]
  61. A.A. Zakari-Issoufou, M. Fallot, A. Porta, A. Algora, J. Tain, E. Valencia, S. Rice, V. Bui, S. Cormon, M. Estienne, et al., Phys. Rev. Lett. 115, 102503 (2015) [CrossRef] [PubMed] [Google Scholar]
  62. A. Algora, D. Jordan, J.L. Taín, B. Rubio, J. Agramunt, A.B. Perez-Cerdan, F. Molina, L. Caballero, E. Nácher, A. Krasznahorkay, M.D. Hunyadi, J. Gulyás, A. Vitéz, M. Csatlós, L. Csige, J. Äysto, H. Penttilä, I.D. Moore, T. Eronen, A. Jokinen, A. Nieminen, J. Hakala, P. Karvonen, A. Kankainen, A. Saastamoinen, J. Rissanen, T. Kessler, C. Weber, J. Ronkainen, S. Rahaman, V. Elomaa, S. Rinta-Antila, U. Hager, T. Sonoda, K. Burkard, W. Hüller, L. Batist, W. Gelletly, A.L. Nichols, T. Yoshida, A.A. Sonzogni, K. Peräjärvi, Phys. Rev. Lett. 105, 202501 (2010) [CrossRef] [PubMed] [Google Scholar]
  63. E. Valencia, J.L. Tain, A. Algora, J. Agramunt, E. Estevez, M.D. Jordan, B. Rubio, S. Rice, P. Regan, W. Gelletly, Z. Podolyák, M. Bowry, P. Mason, G.F. Farrelly, A. Zakari-Issoufou, M. Fallot, A. Porta, V.M. Bui, J. Rissanen, T. Eronen, I. Moore, H. Penttilä, J. Äystö, V.V. Elomaa, J. Hakala, A. Jokinen, V.S. Kolhinen, M. Reponen, V. Sonnenschein, D. Cano-Ott, A.R. Garcia, T. Martínez, E. Mendoza, R. Caballero-Folch, B. Gomez-Hornillos, V. Gorlichev, F.G. Kondev, A.A. Sonzogni, L. Batist, Phys. Rev. C 95, 024320 (2017) [CrossRef] [Google Scholar]
  64. L. San-Felice, R. Eschbach, P. Bourdot, Nucl. Technol. 184, 217 (2013) [Google Scholar]
  65. J. Dickens, T. Love, J. McConnell, R. Peelle, Nucl. Sci. Eng. 78, 126 (1981) [Google Scholar]
  66. S.J. Friesenhahn, N.A. Lurie, https://www.osti.gov/biblio/5847468 [Google Scholar]
  67. J. Leppänen, M. Pusa, T. Viitanen, V. Valtavirta, T. Kaltiaisenaho, Ann. Nucl. Energy 82, 142 (2015) [CrossRef] [Google Scholar]
  68. A.L. Nichols, P. Dimitriou, A. Algora, M. Fallot, L. Giot, F.G. Kondev, T. Yoshida, M. Karny, G. Mukherjee, B.C. Rasco, K.P. Rykaczewski, A.A. Sonzogni, J.L. Tain, Eur. Phys. J. A 59, 78 (2023) [CrossRef] [Google Scholar]
  69. CoNDERC: Compilation of Nuclear Data Experiments for Radiation Characterisation. Tech. rep. (2019), http://www-nds.iaea.org/conderc/ [Google Scholar]
  70. J.K. Dickens, T.A. Love, J.W. McConnell, R.W. Peelle, Nucl. Sci. Eng. 74, 106 (1980) [Google Scholar]
  71. W.A. Schier, G.P. Couchell, β− and gamma Decay Heat Mea-surements Between 0.1 s - 50,000 s for Neutron Fission of 235U, 238U, and 239Pu: Final Report. Tech. Rep. DOE/ER/40723-4 (University of Massachusetts Lowell, 1997) [Google Scholar]
  72. A. Tobias, Derivation of Decay Heat Benchmarks for U-235 and Pu-239 by a Least Squares Fit to Measured Data. Tech. rep. (Central Electricity Generating Board report RD/B/6210/R89, 1989) [Google Scholar]
  73. M.A. Kellett, O. Bersillon, R.W. Mills, OECD/NEA, ISBN 978- 92-64-99087-6 (2009) [Google Scholar]
  74. R.C. Greenwood, R.G. Helmer, M.H. Putman, K.D. Watts, Nucl. Instrum. Meth. Phys. Res. A 390, 95 (1997) [Google Scholar]
  75. V. Guadilla, L. Le Meur, M. Fallot, J.A. Briz, M. Estienne, L. Giot, A. Porta, A. Cucoanes, T. Shiba, A.A. Zakari-Issoufou, A. Algora, J.L. Taβn, J. Agramunt, D. Jordan, M. Monserrate, A. Montaner-Pizá, E. Nácher, S.E.A. Orrigo, B. Rubio, E. Valencia, J. Äystö, T. Eronen, D. Gorelov, J. Hakala, A. Jokinen, A. Kankainen, V. Kolhinen, J. Koponen, I. Moore, H. Penttilä, I. Pohjalainen, J. Reinikainen, M. Reponen, S. Rinta-Antila, K. Rytkönen, V. Sonnenschein, A. Voss, L.M. Fraile, V. Vedia, E. Ganioğlu, W. Gelletly, M. Lebois, J.N. Wilson, T. Martinez, A.A. Sonzogni, Phys. Rev. C 106, 014306 (2022) [CrossRef] [Google Scholar]
  76. B.C. Rasco, M. Wolińska-Cichocka, A. Fijałkowska, K.P. Rykaczewski, M. Karny, R.K. Grzywacz, K.C. Goetz, C.J. Gross, D.W. Stracener, E.F. Zganjar, J.C. Batchelder, J.C. Blackmon, N.T. Brewer, Sh. Go, B. Heffron, T. King, J.T. Matta, K. Miernik, C.D. Nesaraja, S.V. Paulauskas, M.M. Rajabali, E.H. Wang, J.A. Winger, Y. Xiao, C.J. Zachary, Phys. Rev. Lett. 117, 092501 (2016) [CrossRef] [Google Scholar]
  77. A. Fijałkowska, M. Karny, K.P. Rykaczewski, B.C. Rasco, R. Grzywacz, C.J. Gross, M. Wolińska-Cichocka, K.C. Goetz, D.W. Stracener, W. Bielewski, R. Goans, J.H. Hamilton, J.W. Johnson, C. Jost, M. Madurga, K. Miernik, D. Miller, S.W. Padgett, S.V. Paulauskas, A.V. Ramayya, E.F. Zganjar, Phys. Rev. Lett. 119, 052503 (2017) [CrossRef] [Google Scholar]
  78. A.-A. Zakari-Issoufou, M. Fallot, A. Porta, A. Algora, J.L. Taín, E. Valencia, S. Rice, V.M. Bui, S. Cormon, M. Estienne, J. Agramunt, J. Äystö, M. Bowry, J.A. Briz, R. Caballero-Folch, D. Cano-Ott, A. Cucoanes, V.-V. Elomaa, T. Eronen, E. Estévez, G.F. Farrelly, A.R. Garcia, W. Gelletly, M.B. Gómez-Hornillos, V. Gorlychev, J. Hakala, A. Jokinen, M.D. Jordan, A. Kankainen, P. Karvonen, V.S. Kolhinen, F.G. Kondev, T. Martínez, E. Mendoza, F. Molina, I. Moore, A.B. Perez-Cerdán, Zs. Podolyák, H. Penttilä, P.H. Regan, M. Reponen, J. Rissanen, B. Rubio, T. Shiba, A.A. Sonzogni, C. Weber, Phys. Rev. Lett. 115, 102503 (2015) [CrossRef] [PubMed] [Google Scholar]
  79. A. Algora, D. Jordan, J.L. Taín, B. Rubio, J. Agramunt, A.B. Perez-Cerdán, F. Molina, L. Caballero, E. Nácher, A. Krasznahorkay, M.D. Hunyadi, J. Gulyás, A. Vitéz, M. Csatlós, L. Csige, J. Äystö, H. Penttilö, I.D. Moore, T. Eronen, A. Jokinen, A. Nieminen, J. Hakala, P. Karvonen, A. Kankainen, A. Saastamoinen, J. Rissanen, T. Kessler, C. Weber, J. Ronkainen, S. Rahaman, V.-V. Elomaa, S. Rinta-Antila, U. Hager, T. Sonoda, K. Burkard, W. Hüller, L. Batist, W. Gelletly, A.L. Nichols, T. Yoshida, A.A. Sonzogni, K. Peräjärvi, Phys. Rev. Lett. 105, 202501 (2010) [CrossRef] [PubMed] [Google Scholar]
  80. D. Jordan, A. Algora, J.L. Taín, B. Rubio, J. Agramunt, A.B. Perez-Cerdán, F. Molina, L. Caballero, E. Nácher, A. Krasznahorkay, M.D. Hunyadi, J. Gulyás, A. Vitéz, M. Csatlós, L. Csige, J. Äystö, H. Penttilä, I.D. Moore, T. Eronen, A. Jokinen, A. Nieminen, J. Hakala, P. Karvonen, A. Kankainen, A. Saastamoinen, J. Rissanen, T. Kessler, C. Weber, J. Ronkainen, S. Rahaman, V.-V. Elomaa, S. Rinta-Antila, U. Hager, T. Sonoda, K. Burkard, W. Hüller, L. Batist, W. Gelletly, A.L. Nichols, T. Yoshida, A.A. Sonzogni, K. Peräjärvi, A. Petrovici, K.W. Schmid, A. Faessler, Phys. Rev. C 87, 044318 (2013) [CrossRef] [Google Scholar]
  81. M. Kellett, A. Nichols, O. Bersillon, H. Henriksson, R. Jacqmin, B. Roque, J.I. Katakura, K. Oyamatsu, T. Tachibana, T. Yoshida, A. Algora, B. Rubio, J. Tain, C. Dean, W. Gelletly, R. Mills, I. Gauld, P. Möller, A. Sonzogni, Assessment of Fission Product Decay Data for Decay Heat Calculations (2007) [Google Scholar]
  82. M. Kerveno, M. Dupuis, C. Borcea, M. Boromiza, R. Capote, P. Dessagne, G. Henning, S. Hilaire, T. Kawano, A. Negret, M. Nyman, A. Olacel, E. Party, A. Plompen, P. Romain, M. Sin, EPJ Web Conf. 239, 01023 (2020) [Google Scholar]
  83. M. Kerveno, G. Henning, C. Borcea, P. Dessagne, M. Dupuis, S. Hilaire, A. Negret, M. Nyman, A. Olacel, E. Party, A. Plompen, EPJ Nuclear Sci. Technol. 4, 23 (2018) [CrossRef] [EDP Sciences] [Google Scholar]
  84. M. Kerveno, A. Bacquias, C. Borcea, P. Dessagne, G. Henning, L.C. Mihailescu, A. Negret, M. Nyman, A. Olacel, A.J.M. Plompen, C. Rouki, G. Rudolf, J.C. Thiry, Eur. Phys. J. A 51, 167 (2015) [CrossRef] [Google Scholar]
  85. A. Koening, S. Hilaire, M. Duijvestijn, International Conference on Nuclear Data for Science and Technology (EDP Sciences, 2008), pp. 211–214 [Google Scholar]
  86. A. Koening, S. Hilaire, M. Duijvestijn, http://www.talys.eu/ [Google Scholar]
  87. M. Herman, R. Capote, B.V. Carlson, P. Obložinský, M. Sin, A. Trkov, H. Wienke, V. Zerkin, Nucl. Data Sheets 108, 2655 (2007) [CrossRef] [Google Scholar]
  88. T. Kawano, R. Capote, S. Hilaire, P. Chau Huu-Tai, Phys. Rev. C 94, 014612 (2016) [Google Scholar]
  89. T. Kawano, P. Talou, M.B. Chadwick, T. Watanabe, J. Nucl. Sci. Technol. 47, 462 (2010) [CrossRef] [Google Scholar]
  90. E. Browne, J. Tuli, Nucl. Data Sheets 127, 191 (2015) [Google Scholar]
  91. G. Henning, M. Kerveno, P. Dessagne, C. Chatel, F. Claeys, N.D. Bako, M. Dupuis, S. Hilaire, P. Romain, C. de Saint-Jean, R. Capote, M. Boromiza, A. Olacel, A. Negret, C. Borcea, A. Plompen, C. Paradela, M. Nyman, J.C. Drohé, R. Wynants, in 15th International Conference on Nuclear Data for Science and Technology (2022) [Google Scholar]
  92. Evaluated Nuclear Structure Data File (ENSDF) Database, NNDC, Brookhaven National Laboratory, http://www.nndc.bnl.gov/ [Google Scholar]
  93. E. Party, Etude des réactions (n, xn) pour les noyaux fertiles/fissiles du cycle du combustible innovant au Thorium. Theses, Universitéde Strasbourg, (2019), https://tel.archives-ouvertes.fr/tel-02496853 [Google Scholar]
  94. A.M. Demidov, L.I. Govor, V.A. Kurkin, I.V. Mikhailov, Phys. At. Nuclei 71, 1839 (2008) [CrossRef] [Google Scholar]
  95. La structure nucléaire et les données nucléaires pour les réacteurs (2022), https://indico.in2p3.fr/event/20211/ [Google Scholar]
  96. M. Lebois, N. Jovanèević, D. Thisse, R. Canavan, D. Etasse, M. Rudigier, J. Wilson, Nucl. Instrum. Meth. Phys. Res. Sect. A 960, 163580 (2020) [Google Scholar]
  97. C. Chatel, J. Wilson, M. Kerveno, P. Dessagne, G. Henning, 6th International Workshop On Nuclear Data Evaluation for Reactor Applications (WONDER-2023), https://indico.cern.ch/event/982643/book-of-abstracts.pdf [Google Scholar]

Cite this article as: Greg Henning, Abdelhazize Chebboubi, Cyrille De Saint-Jean, Magali Estienne, Muriel Fallot, Lydie Giot, Maëlle Kerveno, Olivier Litaize, Xavier Mougeot, Amanda Porta, Olivier Serot, Vanessa Vallet. Need of precise nuclear structure data for reactor studies, EPJ Nuclear Sci. Technol. 10, 6 (2024)

All Tables

Table 1.

List of potential primary fission fragments having an incomplete level scheme and yield higher than 0.5% in thermal fission of 235U.

In the text
Table 2.

List of important isotopes for fuel cycle applications and that would benefit from a re-evaluation of their decay data.

In the text

All Figures

thumbnail Fig. 1.

Absolute independent fission product yields for the mass A = 139 chain and comparison with the JEFF-3.3 database [24]. Left: all the uncertainties are propagated. Right: the uncertainty associated with was set to 0. Correlation matrices (bottom) in both cases are also displayed showing structures reflecting the analysis procedure. The structures reflect the analysis procedure. In this case, the resolution of the Bateman equations and the normalization procedure are in competition. The figure comes from [19].
In the text
thumbnail Fig. 2.

Impact of a new 235U(nth, f) fission yields evaluation on the decay heat uncertainty calculated for a PWR cell UOX at 45 GWd/t. The library of evaluated data used for the calculation is JEFF-3.3 (full bold black line labeled “JEFF-3.3”). The dashed lines correspond to the uncertainty propagation of nuclear data covariances but where the independent fission yields of 235U(nth, f) have been replaced by one of the new evaluations (thin dashed line: only the variances of independent 235U fission yields are propagated in the Decay heat calculation; bold dashed line: the full variance-covariance matrix of the new 235U fission yields evaluation are propagated).
In the text
thumbnail Fig. 3.

Impact of the new JEFF-3.3 decay data and fission yield library on the Dickens fission burst experiment (gamma heat on the left, total heat on the right).
In the text
thumbnail Fig. 4.

Performances of the JEFF-3.1.1 and JEFF-3.3 libraries on Friesenhahn fission burst experiment (irradiation time = 1 d).
In the text
thumbnail Fig. 5.

235U thermal fission decay heat as a function of cooling time obtained with the JEFF-3.1.1 and JEFF-3.3 libraries with the addition of TAGS data [58, 75–77]. Experimental was taken from the CoNDERC IAEA database [69].
In the text
thumbnail Fig. 6.

239Pu thermal fission decay heat as a function of cooling time obtained with the JEFF-3.1.1 and JEFF-3.3 libraries with the addition of TAGS data [58, 75–77]. Experimental was taken from the CoNDERC IAEA database [69].
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.