EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 7 (2021) EPJ Nuclear Sci. Technol., 7 (2021) 16 Full HTML
Open Access
Issue
EPJ Nuclear Sci. Technol.
Volume 7, 2021
Article Number 16
Number of page(s) 6
DOI https://doi.org/10.1051/epjn/2021015
Published online 23 September 2021

© O. Pakari et al., Published by EDP Sciences, 2021

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

In nuclear reactor design and radiation protection, one typically relies on power normalization [1] and a validated code to predict the radiation field. An important contributor to the ambient dose and structural heating is the gamma radiation emitted in nuclear processes. Moreover, the heating contribution due to gamma rays can exceed 90% in the reflector of light water reactors [2,3], highlighting the need to accurately predict the field and energy deposition of gamma rays [4]. Common codes for reactor neutronics typically do not include photon transport, or include it only for prompt processes. Monte Carlo codes such as Serpent 2 [5] have been improved to include coupled neutron-photon transport modes [6] that allow for mixed neutron gamma field calculations, with improvements to energy deposits and delayed particle transport [7] added recently. However, many nuclear data libraries do not include all relevant prompt or delayed emission data [8] in order to provide the full picture [9]. As the delayed contribution of the total gamma flux, or delayed gamma fraction, is typically of the order of 30% [3,10–13], the knowledge and accurate experimental determination of this fraction can aid in validating these codes.

Recent experiments to determine the delayed gamma fraction to date include flux measurements in research reactors [13–15] using ionization chambers. The CROCUS zero power reactor at EPFL in Switzerland offers a flexible environment to conduct gamma field measurements, using the newly developed LEAF system based on scintillators [16]. In this paper we present the delayed gamma fraction determination in CROCUS, highlighting the theoretical basis, experimental setup, our flexible analysis methodology, and discuss the results.

2 Delayed gamma fraction estimation technique

A general technique that allows for the experimental determination of the delayed gamma fraction has yet to be established. In a recent study [17], the simultaneous measurement of a fission chamber and an ionization chamber were used. The corresponding neutron and gamma signals were normalized to a point in time where the reactor had just reached power, and then, following a reactor shutdown, the delayed gamma fraction was determined from the difference in signals. The fundamental principle is that once the reactor is shut down, the prompt neutrons and thus also prompt gammas die away. The remaining delayed neutrons inducing prompt gamma releases are then recorded by the fission chamber and removed from the remaining gamma signal to yield the delayed gamma signal. By finding the reduced gamma signal directly after shutdown, we expect to only measure a delayed gamma signal that allows for the fraction to be determined when comparing to the signal at power. The method used in [17] is however only applicable to higher power systems, such as the TRIGA reactor, because of the assumption of negligible background from previous activation. Therefore, in the specific case of a zero power reactor, we are required to develop amore general method. As we will outline, our proposed methodology is usable both for zero power and power systems, and can be adapted to learn about the specific time constants of a given systems’ activation environment.

We define the time dependent signal of a gamma detector in a reactor Sγ as the sum of the prompt contributions Sγ,p and delayed contributions Sγ,d: 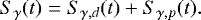S γ (t)= S γ,d (t)+ S γ,p (t). \begin{equation*} S_{\gamma}(t) = S_{\gamma,d}(t) + S_{\gamma,p}(t). \end{equation*}(1)

Assuming that the prompt gamma signal is proportional to the neutron signal Sn, we may find the delayed gamma signal as 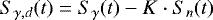S γ,d (t)= S γ (t)−K⋅ S n (t) \begin{equation*} S_{\gamma,d}(t) = S_{\gamma}(t) - K\cdot S_{n}(t) \end{equation*}(2)

with K being the ratio between the steady state signals 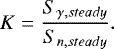K= S γ,steady S n,steady . \begin{equation*} K = \frac{S_{\gamma,steady}}{S_{n,steady}}. \end{equation*}(3)

By now normalizing by the gamma detector signal at steady state, Sγ,steady, we find: 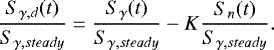S γ,d (t) S γ,steady = S γ (t) S γ,steady −K S n (t) S γ,steady . \begin{equation*} \frac{S_{\gamma,d}(t)}{S_{\gamma,steady}} = \frac{S_{\gamma}(t)}{S_{\gamma,steady}} - K \frac{ S_{n}(t)}{S_{\gamma,steady}}. \end{equation*}(4)

The term on the left hand side is our desired delayed gamma fraction Sγ,d,norm, we write 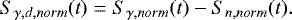S γ,d,norm (t)= S γ,norm (t)− S n,norm (t). \begin{equation*} S_{\gamma,d,norm}(t) = S_{\gamma,norm}(t) -S_{n,norm}(t). \end{equation*}(5)

Directly after a reactor shutdown, i.e. the insertion of a large negative reactivity on the order of dollars, the prompt signal goes to zero and only the delayed gamma signal remains. By least squares fitting the ensuing multi-exponential decay of the gamma signal, and evaluating said fit function at the time of shutdown, we deduce the delayed gamma fraction at steady state operation. The end result depends however on the scaling factor K, which is dependent on the time the steady state signal is chosen. In previous studies this time instant was arbitrary (e.g. the reactor operator assumes a critical reactor). In order to accurately capture the relevant delayed signal, a given experiment would need to run long enough to allow for the short lived delayed gamma source to build up. In our experimental setup, detailed in Section 3, we use a “system agnostic” approach on the normalization time. By sampling over the whole signal, we can observe the most relevant build-up of the delayed source and thus choose a normalization time that best captures the reactor dependent short-lived isotope build-up. Simultaneously, this method acts as a method to sample the experimental data to gather statistics on the uncertainty on the delayed gamma fraction related to the factor K. We note here that the delayed gamma fraction is only determined for a given time instant, as burnup and long lived activation naturally leads to a steady increase of delayed gamma sources. This long-lived build-up is however not visible in our experiment, as expected from a zero power system.

3 Experimental setup

In this section we present the CROCUS zero power reactor and the configuration and experimental setup used for the delayed gamma fraction determination.

3.1 The zero power research reactor CROCUS

A full description of the core can be found in the International Reactor Physics Experiments Handbook (IRPhE) [18,19]. The CROCUS reactor is a two-zone, uranium-fueled, H2O-moderated critical assembly operated by the Laboratory for Reactor Physics and Systems Behaviour (LRS) at the Swiss Federal Institute of Technology Lausanne (EPFL). It is a zero power reactor, with a maximum power of up to 100 W. The core is approximately cylindrical in shape with a diameter of about 58 cm and a height of 100 cm. Two different kinds of fuel rods in interlocked zones make up the reactor core of CROCUS (see Figs. 1 and 2). The inner zone is loaded with 336 UO2 fuel rods (1.806 wt.%-enriched), set in a square lattice with a pitch of 1.837 cm. The outer zone is loaded with up to 176 thicker, Umet fuel rods (0.947 wt.%-enriched) with a pitch of 2.917 cm, also in a square lattice. All fuel rods are cladded with aluminum and are maintained in a vertical position by the upper grid and lower grid plates spaced 100 cm apart. The active fuel length starts at the top surface of the lower grid’s cadmium layer and extends to 100 cm. The core is located in an aluminum water tank, its diameter is 130 cm and thickness is 1.2 cm. Demineralized light water is used as moderator and reflector. Reactivity is nominally controlled by a variation of the water level using a spillway with an accuracy of 0.1 mm (equivalent to 0.4 pcm) and optionally by means of two control rods containing naturally enriched boron carbide (B4C) sintered pellets located in diagonal symmetry within the outer fuel zone.

thumbnail Fig. 1

Schematic isometric view of the CROCUS reactor (left), and top view of the core configuration (right).
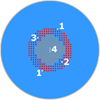thumbnail Fig. 2

Top view of the CROCUS reactor configuration used for the delayed gamma fraction experiment. 1. BF3 detectors, 2. CeBr3 scintillator, 3. control rod, 4. mounted cadmium blade. At a given stable reactor condition, the cadmium blade is dropped into the center to introduce a large negative reactivity and effectively SCRAM the reactor. The prompt contribution of radiation is thereafter considered eliminated, and the delayed gamma fraction can be determined.

3.2 Simultaneous in-core neutron and gamma detection

CROCUS has a recent history of neutron detector developments, such as fission chambers in current mode [20,21], fiber based miniature scintillators for neutron detection [22,23], or diamond based semiconductor detectors [24]. Gamma detection capabilities were added in the form of the LEAF system, an array of four scintillation based gamma spectrometers [16,25]. For this particular experiment, we chose Transcommerce MN-1 BF3 detectors [26–28] to measure the neutron signal in two peripheral locations, and LEAF’s CeBr3 detector to measure the gamma signal in a control rod tube – all set at mid core height (see Fig 2). The acquisition layout is shown in Figure 3. All detectors’ lower level thresholds were determined via standard pulse height analysis using an Ortec 926 Multi Channel Buffer [16,29]. Note that the scintillators provide the gamma spectrum and could in principle also allow for energy dependent measurements. For an overview for the gamma spectra obtained in this location we refer to [25].

thumbnail Fig. 3

Acquisition layout for the delayed gamma fraction experiment. The acquisition system can handle up to four pulse signals fromneutron detectors [30].

3.3 Delayed gamma fraction experiment

The overall timeline of the experiment follows the theoretical considerations mentioned before: the reactor is brought to power, and then, after sufficient time to allow for the delayed gamma source to build up, is shut down. CROCUS has several safety systems that activate altogether in case of a shutdown, notably the opening of the valves of the external expansion tanks causing the water level to drop rapidly (within 1 s), and the drop of the two cruciform safety blades into the core center. The drop of the water level causes significant mechanical vibrations that typically induce noise in detection equipment. Furthermore, the safety blades cannot be dropped independently of the water level. For this experiment, we therefore mounted an additional cadmium blade above the core that can be dropped by the operator to effectively shut down the reactor. The drop mechanism is a well characterized system that is also used for the power calibration of the reactor when irradiating gold foils [1]. The blades’ worth was estimated to be around 3500 pcm [31].

The time series of the neutron and gamma detectors during the whole experiment are displayed in Figure 4. The reactor operator announces when the reactor has reached a critical state (tStab). After allowing for a build up time of around 20 min, the cadmium blade is dropped into the core at tSCRAM to shut down the reactor. Since the delayed gamma fraction diverges for infinite operation time, we chose the arbitrary time interval of 20 min for build-up. This value is corroborated by our results (see Sect. 4), as we observe a significant build-up in the first minutes and thereafter a plateau. Note that the reactor’s PuBe startup source was retracted from below the core before reaching the desired power level, leaving only delayed neutrons and a negligible spontaneous fission contribution after the blade drop.

thumbnail Fig. 4

Signals acquired from the neutron and gamma detectors during the delayed gamma fraction experiment. The signals are normalized to the time of cadmium blade insertion, tSCRAM. The reactor was considered critical and thus stable by the operator at approximately tStab.

3.4 Delayed gamma fraction determination

As discussed in Section 2, we determine the delayed gamma fraction by normalizing the neutron and gamma signals to a time after stabilization tStab, and fitting the delayed gamma signal with a two termed exponential decay model from tSCRAM to tend, see Figure 5. To avoid any induced mechanical noise by the automatic reactor shutdown at low flux signals, tend was chosen as the point when the safety system triggered. The fitted function is then evaluated at the time of blade insertion tSCRAM to yield the delayed gamma fraction estimate.

The improved, “system agnostic” method of the delayed gamma fraction estimation lies in treating the normalization time as variable. The signal normalization time instant should be after the delayed gamma source has built-up, i.e. that relevant short-lived activation products have reached a quasi-equilibrium. This time instant is system specific, as it depends on the reactor’s materials. We thus left the normalization time as variable and determined the delayed gamma fraction for 100 samples in the time interval between the time of stabilized reactor power tStab and the blade insertion time tSCRAM, leading to an interval of 12 seconds between samples. This allows for two advantages: Firstly, we can observe the delayed gamma source change with normalisation time and therefore determine when the important sources, such as aluminium activation, have built up to significant levels. By fitting the decrease in gamma fraction with an exponential decay we can use a decision threshold above whichthe final estimate is based on. In this work we use 95%. Secondly, we can estimate any spread in the data and give a more reliable uncertainty bound compared to the parameter uncertainty from the least squares fit.

thumbnail Fig. 5

Example of a resulting delayed gamma signal when choosing a signal normalization point before the cadmium blade is inserted (tSCRAM-). The curve is fitted with an exponential decay model until tend; the function value evaluated at tSCRAM+ is the delayed gamma fraction.

4 Results and discussion

The final results are displayed in Table 1, with a visualization of the sampling results shown in Figure 6. By using the normalization time as variable, we can observe the relative change in measured delayed gamma fraction in dependence of the experiment’s timeline from tStab to time tSCRAM. The estimated delayed gamma fraction at first decreases and then stabilizes around a mean value after about 8 minutes. The apparent decrease is due to the fact that the total gamma signal is still increasing significantly after the operator defined tStab. As the delayed gamma signal is a fixed value, we thus observe a decrease in the estimated delayed gamma fraction. This decrease is therefore an indication that the most important source of delayed gammas in CROCUS, on top of the fuel’s background gammas, is the short term activation of the materials. Given the half life of the neutron activation product 28Al of 2.2 minutes, we hypothesize this to be the major cause for the build-up we observe [32]. The observed gamma spectra using LEAF [25] show several lines that can be attributed to 27Al(n,x) interactions,yet a more causal relationship has yet to be established in future work by e.g. a time dependent observation of said line emissions.

The final estimate for the delayed gamma fraction is found as displayed in Figure 6 after applying a 95% build-up threshold. We emphasize that we also plot the least squares fit uncertainties on the estimated delayed gamma fraction in each point –which in each case amounts to between 0.2% and 0.5%. In the spread of the sampled values we can however see that this uncertainty underestimates the total spread seen across all samples. Using the accepted samples’ mean and standard deviation we therefore provide a truer estimate of the spread. Using either the northern or southern BF3 as reference neutron signal, we find the delayed gamma fraction to agree within the estimated sampling based uncertainties – giving a delayed gamma fraction of (30.50± 0.57)% (with reference north) and (30.63± 0.62)% (with reference south) in the control rod tube of CROCUS. The variance weighted mean gives (30.55± 0.61)%. We note that this value is dependent on the gamma detector’s location, as discussed in [17]. With increasing distance of the gamma detector to the core center, the fraction decreases due to an apparent difference in the prompt and delayed gamma’s mean free paths. The neutron detector’s location is expected to not change the result save for spatial effects (negligible in CROCUS [33]) and statistical errors arising from detectors set into low flux regions.

This method of observing the build-up should be generally applicable to other reactors, thus allowing for a consistent method to estimate the delayed gamma fraction among facilities.

Table 1

Final delayed gamma fractions determined via the sampling technique using two different neutron signals as reference. The variance weighted average with standard error on the weighted mean is also given.

thumbnail Fig. 6

Top: delayed gamma fraction determined for a set of fits with the signal normalization set between the stabilization of the reactor power tStab and the insertion of the cadmium blade tSCRAM, using either BF3 detector as neutron signal reference. A build-up of the delayed gamma signal can be seen – presenting here as an exponential reduction in delayed gamma fraction. After about 8 min a saturation of build-up is seen. Bottom: by using the fitted exponential decay, we used the arbitrary threshold of having observed 95% of the fitted decay we determine the respective delayed neutron fraction estimate by estimating the mean and standard deviation of all accepted samples.

5 Conclusion

The delayed gamma fraction is an important experimental quantity, e.g. for code validation of recent Monte Carlo codes that include delayed emissions to estimate nuclear emission database needs. The CROCUS zero power reactor allows for a flexible environmentto measure this quantity using its neutron and gamma detection capabilities. We demonstrated a method on how to estimate thedelayed gamma fraction that is transferable to other facilities and discuss how the method allows both for more physical insights and better uncertainty estimation. Using in-core instrumentation measuring neutron and gamma signals, we determined the delayed gamma fraction in the control rod tube at mid core height to be (30.50 ± 0.57)% and (30.63 ± 0.62)% depending on the choice of reference signal, and a combined value of (30.55 ± 0.61)%.

Author contribution statement

O. Pakari: conceptualization, investigation, formal analysis, writing , T. Mager: investigation, software, methodology, V. Lamirand: validation, writing, supervision, P. Frajtag: investigation, resources, supervision, A. Pautz: project administration, funding acquisition.

References

  1. V. Lamirand, A. Laureau, O. Pakari, P. Frajtag, A. Pautz, Power calibration methodology at the CROCUS reactor, EPJ Web Conf. 225, 04022 (2020) [CrossRef] [Google Scholar]
  2. D. Fourmentel, J.-F. Villard, A. Lyoussi, C. Reynard-Carette, G. Bignan, J.-P. Chauvin, C. Gonnier, P. Guimbal, J.-Y. Malo, M. Carette et al., Combined analysis of neutron and photon flux measurements for the Jules Horowitz Reactor core mapping, in 2011 2nd International Conference on Advancements in Nuclear Instrumentation, Measurement Methods and their Applications (IEEE, 2011) [Google Scholar]
  3. H. Amharrak, J.D. Salvo, A. Lyoussi, M. Carette, C. Reynard-Carette, State of the art on nuclear heating in a mixed (n/γ) field in research reactors, Nucl. Instr. Methods Phys. Res. A 749, 57–67 (2014) [CrossRef] [Google Scholar]
  4. G. Rimpault, D. Bernard, D. Blanchet, C. Vaglio-Gaudard, S. Ravaux, A. Santamarina, Needs of accurate prompt and delayed γ-spectrum and multiplicity for nuclear reactor designs, Phys. Proc. 31, 3–12 (2012) [CrossRef] [Google Scholar]
  5. J. Leppönen, M. Pusa, T. Viitanen, V. Valtavirta, T. Kaltiaisenaho, The Serpent Monte Carlo Code: Status, Development and Applications in 2013, in SNA MC 2013 – Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo, edited by D. Caruge, C. Calvin, C. Diop, F. Malvagi, J.C. Trama (EDP Sciences, 2014) [Google Scholar]
  6. J. Leppänen, T. Kaltiaisenaho, V. Valtavirta, M. Metsälä, Development of a coupled neutron / photon transport mode in the serpent 2 Monte Carlo code, in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, M&C 2017 (2017) [Google Scholar]
  7. R. Tuominen, V. Valtavirta, J. Leppänen, New energy deposition treatment in the serpent 2 monte carlo transport code, Ann. Nucl. Energy 129, 224–232 (2019) [CrossRef] [Google Scholar]
  8. S. Ravaux, D. Bernard, A. Santamarina, New evaluation of photon production for JEFF-3, EPJ Web Conf. 42, 04002 (2013) [CrossRef] [Google Scholar]
  9. S. Oberstedt, R. Billnert, A. Gatera, W. Geerts, P. Halipré, F.-J. Hambsch, M. Lebois, A. Oberstedt, P. Marini, M. Vidali et al., Prompt fission γ-ray spectra characteristics - a first summary, Phys. Proc. 64, 83–90 (2015) [CrossRef] [Google Scholar]
  10. K. Ambrožič, D. Fourmentel, H. Carcreff, V. Radulović, L. Snoj, Computational support on the development of nuclear heating calorimeter detector design, EPJ Web Conf. 225, 04033 (2020) [CrossRef] [Google Scholar]
  11. K. Ambrožič, L. Snoj, Characterization of gamma field in the JSI TRIGA reactor, Ph.D. thesis, University of Ljubljana, Faculty of Mathematics and Physics (2020) [Google Scholar]
  12. D. Blanchet, N. Huot, P. Sireta, H. Serviere, M. Boyard, M. Antony, V. Laval, P. Henrard, Qualification of a gamma-ray heating calculation scheme for the future jules horowitz material testing reactor (RJH), Ann. Nucl. Energy 35, 731–745 (2008) [CrossRef] [Google Scholar]
  13. D. Fourmentel, C. Reynard-Carette, A. Lyoussi, J.F. Villard, J.Y. Malo, M. Carette, J. Brun, P. Guimbal, Y. Zerega, Nuclear heating measurements in material testing reactor: a comparison between a differential calorimeter and a gamma thermometer, IEEE Trans. Nucl. Sci. 60, 328–335 (2013) [Google Scholar]
  14. D. Fourmentel, P. Filliatre, J.-F. Villard, A. Lyoussi, C. Reynard-Carette, H. Carcreff, Measurement of photon flux with a miniature gas ionization chamber in a material testing reactor, Nucl. Instr. Methods Phys. Res. Sect. A 724, 76–82 (2013) [CrossRef] [Google Scholar]
  15. D. Fourmentel, V. Radulovic, L. Barbot, J-F. Villard, G. Zerovnik, L. Snoj, M. Tarchalski, K. Pytel, F. Malouch, Delayed gamma measurements in different nuclear research reactors bringing out the importance of the delayed contribution in gamma flux calculations, in 2015 4th International Conference on Advancements in Nuclear Instrumentation Measurement Methods and their Applications (ANIMMA) (IEEE, 2015) [Google Scholar]
  16. O.V. Pakari, Experimental and numerical study of stochastic branching noise in nuclear reactors, Ph.D. thesis, École polytechnique fédérale de Lausanne (EPFL, 2020) [Google Scholar]
  17. K. Ambrožič, A. Gruel, V. Radulović, M.L. Guillou, P. Blaise, C. Destouches, L. Snoj, Delayed gamma determination at the JSI TRIGA reactor by synchronous measurements with fission and ionization chambers, Nucl. Instr. Methods Phys. Res. A 911, 94–103 (2018) [CrossRef] [Google Scholar]
  18. U. Kasemeyer, R. Früh, J.M. Paratte, R. Chawla, Benchmark on kinetic parameters in the CROCUS reactor, in International Reactor Physics Experiments Handbook (IRPhE), no. 4440, OECD (2007) [Google Scholar]
  19. J.M. Paratte, R. Früh, U. Kasemeyer, M.A. Kalugin, W. Timm, R. Chawla, A benchmark on the calculation of kinetic parameters based on reactivity effect experiments in the CROCUS reactor, Ann. Nucl. Energy 33, 739–748 (2006) [CrossRef] [Google Scholar]
  20. O. Pakari, V. Lamirand, G. Perret, L. Braun, P. Frajtag, A. Pautz, Current Mode Neutron Noise Measurements in the Zero Power Reactor CROCUS, in EPJ Web of Conferences (EDP Sciences, 2018), Vol. 170, p. 04017 [Google Scholar]
  21. O. Pakari, V. Lamirand, G. Perret, P. Frajtag, A. Pautz, Kinetic parameter measurements in the crocus reactor using current mode instrumentation, IEEE Trans. Nucl. Sci. (2018) [Google Scholar]
  22. F. Vitullo, V. Lamirand, J.-B. Mosset, P. Frajtag, O. Pakari, G. Perret, A. Pautz, A mm3 fiber-coupled scintillator for in-core thermal neutron detection in CROCUS, IEEE Trans. Nucl. Sci. 67, 625–635 (2020) [CrossRef] [Google Scholar]
  23. F. Vitullo, V. Lamirand, J.-B. Mosset, P. Frajtag, O. Pakari, P. Gregory, A. Pautz, Developing and testing a miniature fiber-coupled scintillator for in-core neutron counting in CROCUS, EPJ Web Conf. 225, 04018 (2020) [CrossRef] [Google Scholar]
  24. M. Hursin, C. Weiss, P. Frajtag, V. Lamirand, G. Perret, P. Kavrigin, A. Pautz, E. Griesmayer, Testing of a sCVD diamond detection system in the CROCUS reactor, Eur. Phys. J. A 54 (2018) [CrossRef] [Google Scholar]
  25. O. Pakari, V. Lamirand, T. Mager, A. Laureau, P. Frajtag, A. Pautz, First in-core gamma spectroscopy experiments in the zero power reactor crocus, in ANIMMA 2021 Conference Proceedings (2021) [Google Scholar]
  26. G. Perret, Tm-41-14-02 rev. 1: Decay constant and delayed neutron fraction measurements in crocus, Tech. rep., ERP, LRS, Paul Scherrer Institut (2014) [Google Scholar]
  27. O.V. Pakari, Development of current and fast neutron noise measurements in CROCUS, Master’s thesis, École polytechnique fédérale de Lausanne (EPFL, 2016), http://infoscience.epfl.ch/record/253177 [Google Scholar]
  28. V. Lamirand, G. De Izarra, A. Krása, G. Perret, O. Pakari, P. Frajtag, M. Hursin, P. Blaise, J. Wagemans, A. Pautz, Intercomparison of neutron noise measurement systems in the CROCUS reactor, in Proc. PHYSOR (2018) [Google Scholar]
  29. Ortec 926 MCB, Datasheet (2019), www.ortec-online.com/download/926-MNL.pdf [Google Scholar]
  30. G. Perret, B. Geslot, A. Gruel, P. Blaise, J. Di-Salvo, G. De Izarra, C. Jammes, M. Hursin, A. Pautz, Kinetic parameter measurements in the minerve reactor, IEEE Trans. Nucl. Sci. 64, 72–734 (2017) [CrossRef] [Google Scholar]
  31. V. Lamirand, Installation nucléaire CROCUS - rapport de sécurité, Tech. rep., LRS Internal Report No 15-48 (2016) [Google Scholar]
  32. D.E. Alburger, G.A.P. Engelbertink, Half-lives ofBe11, c15, n16, o19, andAl28, Phys. Rev. C 2, 1594–1596 (1970) [CrossRef] [Google Scholar]
  33. O. Pakari, V. Lamirand, G. Perret, D. Godat, M. Hursin, P. Frajtag, A. Pautz, Investigation of spatial effects on neutron noise measurements in the zero power reactor CROCUS, in PHYSOR, Cancun, Mexico (2018) [Google Scholar]

Cite this article as: Oskari Pakari, Tom Mager, Vincent Lamirand, Pavel Frajtag, Andreas Pautz, Delayed gamma fraction determination in the zero power reactor CROCUS, EPJ Nuclear Sci. Technol. 7, 16 (2021)

All Tables

Table 1

Final delayed gamma fractions determined via the sampling technique using two different neutron signals as reference. The variance weighted average with standard error on the weighted mean is also given.

In the text

All Figures

thumbnail Fig. 1

Schematic isometric view of the CROCUS reactor (left), and top view of the core configuration (right).
In the text
thumbnail Fig. 2

Top view of the CROCUS reactor configuration used for the delayed gamma fraction experiment. 1. BF3 detectors, 2. CeBr3 scintillator, 3. control rod, 4. mounted cadmium blade. At a given stable reactor condition, the cadmium blade is dropped into the center to introduce a large negative reactivity and effectively SCRAM the reactor. The prompt contribution of radiation is thereafter considered eliminated, and the delayed gamma fraction can be determined.
In the text
thumbnail Fig. 3

Acquisition layout for the delayed gamma fraction experiment. The acquisition system can handle up to four pulse signals fromneutron detectors [30].
In the text
thumbnail Fig. 4

Signals acquired from the neutron and gamma detectors during the delayed gamma fraction experiment. The signals are normalized to the time of cadmium blade insertion, tSCRAM. The reactor was considered critical and thus stable by the operator at approximately tStab.
In the text
thumbnail Fig. 5

Example of a resulting delayed gamma signal when choosing a signal normalization point before the cadmium blade is inserted (tSCRAM-). The curve is fitted with an exponential decay model until tend; the function value evaluated at tSCRAM+ is the delayed gamma fraction.
In the text
thumbnail Fig. 6

Top: delayed gamma fraction determined for a set of fits with the signal normalization set between the stabilization of the reactor power tStab and the insertion of the cadmium blade tSCRAM, using either BF3 detector as neutron signal reference. A build-up of the delayed gamma signal can be seen – presenting here as an exponential reduction in delayed gamma fraction. After about 8 min a saturation of build-up is seen. Bottom: by using the fitted exponential decay, we used the arbitrary threshold of having observed 95% of the fitted decay we determine the respective delayed neutron fraction estimate by estimating the mean and standard deviation of all accepted samples.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.