| Issue |
EPJ Nuclear Sci. Technol.
Volume 6, 2020
|
|
|---|---|---|
| Article Number | 50 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/epjn/2020012 | |
| Published online | 01 July 2020 | |
https://doi.org/10.1051/epjn/2020012
Regular Article
Newton’s second law analogy for the traveling wave of nuclear burning
1
M. Smoluchowski Institute of Physics, Jagiellonian University,
30348
Krakow,
Poland
2
Odessa National Polytechnic University,
Shevchenko av. 1,
Odessa
65000,
Ukraine
* e-mail: vitaliyurbanevich@gmail.com
Received:
16
September
2019
Received in final form:
25
May
2020
Accepted:
28
May
2020
Published online: 1 July 2020
We consider a model of neutron-nuclear wave burning. The traveling wave of nuclear burning of the medium is initiated by an external neutron source and is the basis for the new generation reactors the so-called “traveling-wave reactors”. We develop a model of nuclear traveling wave burning, for which it is possible to draw a Newton’s second law analogy with a mechanical dissipative system. On the basis of this analogy, we find that the wave velocity has a continuous spectrum bounded below. Within the framework of the new model, we show the autowave to be possible for certain neutron energies only. Also we find that two burning modes are possible depending on the control parameters: a traveling autowave and a wave driven by an external neutron source.
© V. Urbanevych et al., published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The idea of autowave (or traveling-wave) regime in the medium with diffusion and multiplication of neutrons was suggested in the paper [1] more than 30 yr ago. In [2] authors give the equations which describe a physical system with a possible nuclear burning. These equations take into account among others the multi-stageness of burn-up reactions, the neutrons energy distribution and the possible dependence of the diffusion coefficient on the energy, time, and coordinate. These equations are too complicated for the exact analytical solutions being looked for, so one has to seek either for the simplified systems of equations or the numerical simulations. In a number of papers [1,3–8] authors regard significantly simplified expressions for this system. Using it, they try to analyze physical effects and look for the traveling-wave solutions to this problem. In present work, we consider the system of equations, similar to one from [1] and [8], but we suggest a different way to analyze it. Substantial difference between models of [1,4,7,8] and [3,5,6,9] consists lies in describing the combustion processes. In [3] author regards only one differential equation for the neutrons diffusion, what implies that the nonlinearity and nonlocality of the system are regarded as an effect of the fuel’s combustion, while the equations which describe these processes are not considered at all. In [5,6,9] all the kinetic equations for the fuel’s combustion do not have terms which are not proportional to the neutron flux and could provide the system with a contribution of the β-decay. Neglecting of these terms leads to the appearance of the integrals, which are not instilled in the original system. Considering these terms makes impossible to apply the methods, similar to that in [5,9]. There is an important difference in [1,8,10] and [5,11] and it is that in the differential equations we have some terms which are not proportional to the neutron flux and are responsible for the β-decay. Considering these terms makes impossible to apply the methods, similar to that in [5,11].
In [8] the numerical simulation was performed only with time-constant external neutron flux. Since the system is not left to itself in such a mode, one can question the interpretation of these results as autowave. In addition, the numerical calculation does not give an answer to two important, from our point of view, questions. Firstly, what are the conditions, which would lead the system of equations to the autowave solution? And secondly, where the speculations about conditions for the wave velocity come from? In [1,4,7] authors used an analogy with an eigenvalue problem in the famous Schrödinger equation in order to answer these two questions. In our opinion, the inconsistency in [1,4,7] arises from the fact that in the Schrödinger equation, potential does not depend on the eigenfunction, which is being looked for, while the analog of this potential in the system from [1] does depend by means of burn-up equations Besides that, the eigenfunction of the Schrödinger equation can take a negative value, in spite of the neutrons density. We would like to demonstrate that the analysis of the problem like in [1,4,7] can be performed using the analogy with the dynamic equation from the classical mechanics instead of the quantum equation which was used there. In such a new analogy the coordinate is substituted by the integral over the neutrons density, and time – by the autowave variable. In such case, the “force” (here and below the quotation marks mean, that it is not this physical quantity, but just its analog within our model) in the equation is consisted of the potential and dissipative parts. It comes to light that the traveling-wave mode is possible only when the “potential energy” function has the minimum point, which in classical mechanics led to the regime with oscillations. If the oscillations appear than in some part the velocity should become negative. As in our case, “the velocity” is proportional to the neutrons density, the solutions with the negative velocity leads to the unphysical negative neutrons density. The presence of dissipation can prevent the system from the negative velocity values if all initial stored “energy” will be dissipated before the minimum point is reached. Similarly, the ball in the elastic pendulum, which is brought out of the equilibrium in a very viscous medium will be able just to return to the equilibrium point, but not to oscillate. It will be shown below, that the “dissipative” contribution is directly connected to the β-decay processes, which are not taken into account in [5,9], and it is appeared to be proportional to the autowave velocity. Out of it, we come to the condition for this velocity - it has to be such, that “dissipation” would not allow oscillations. Hence the restrictions for the eigenvalues spectrum in the regarded model appear not out of the boundary conditions, but out of the non-negative solution requirement. We perceive the main difference of our work from another in this area, as e.g. in [1,4,7] the spectrum comes out from the boundary conditions.
Different kinds of nonlinear equations are being analyzed in [12]. In the paper, authors find the traveling-wave velocity from the condition that there is some phase trajectory in such a system, that connects points, consistent with the boundary conditions. A similar way of finding the wave velocity is used in [9], but using only the part of the trajectory, which corresponds to the positive (that is physical) values of neutron flux. But this path is being built with the help of integral, which can lead to an unphysical branch with negative values because of the square of neutrons’ flux in it. These two branches are connected in the origin of thecoordinates and the transition between the branches can happen at that point. Finally, the nonlinear eigenvalue problem in [11] is not concerning the velocity, but the effective multiplication coefficient. Again, the authors find the eigenvalues requiring that there is a nontrivial solution in such a system, which satisfies the boundary conditions.
We find that the traveling-wave velocities spectrum, which is determined by the condition of the non-negativity of the solution, is continuous and limited from below. Looking at the results of [12], such a situation is typical for the nonlinear autowaves. Next, we will discuss the above considerations in more detail. In Section 6 we will analyze the possible connection between the obtained results and more realistic models.
2 System of kinetic equations
Let us start with the system of kinetic (balance) equations for neutrons and nuclides, which describe the process of wave neutron-nuclear burning of the uranium-plutonium fissile medium. We use the work by L.P. Feoktistov [1] as a basis. Note that the system considered further on has a simplified form. As in [1], the equations describing the fission fragments are omitted, and the fuel consists only of 238U and there are no fissile nuclides like 235U, as in [13].
Let us first consider the equation for neutrons. With the mentioned simplifications in the diffusion approximation it looks as follows:
 (1)
(1)
where n, n8, n9 and nPu are the dimensionless concentrations of neutrons, 238U, 239U and 239 Pu respectively (all the concentrations are dimensionless and normalized by the initial concentration of 238U–N ); σc,i is the neutron capture cross-sectionfor the ith nuclide, σf,i is the fission cross-section, σa,i is the neutron absorption cross-section (σa,i = σf,i + σc,i); D is the neutron diffusion coefficient; ν is the average number of neutrons produced per one 239Pu fission reaction.
); σc,i is the neutron capture cross-sectionfor the ith nuclide, σf,i is the fission cross-section, σa,i is the neutron absorption cross-section (σa,i = σf,i + σc,i); D is the neutron diffusion coefficient; ν is the average number of neutrons produced per one 239Pu fission reaction.
Quantities  ,
,  ,
,  , and
, and  have the dimension of inverse time. So one can treat them as the inverse mean free times for the neutrons with respect to the corresponding nuclear reaction with relevant nucleus, given the nuclei concentrations
have the dimension of inverse time. So one can treat them as the inverse mean free times for the neutrons with respect to the corresponding nuclear reaction with relevant nucleus, given the nuclei concentrations  . Therefore, they may be denoted as follows:
. Therefore, they may be denoted as follows:
 (2)
(2)
However, the introduced mean free times are approximately equal. At least, the difference between them is much less than their difference from the overall time scale of the problem – the characteristic time of β-decay τβ. So in our work we apply a simplification, that
 (3)
(3)
In addition, one can switch to the dimensionless time coordinate, which is normalized by the τ and spatial coordinate x, defined as follows:
 (4)
(4)
All these simplifications bring the equation (1) to the next form:
 (5)
(5)
Next, we would like to formulate the kinetic equations which we mentioned in the introduction. These equations will be responsible for the fuel combustion with a next chain of reactions:
 (6)
(6)
We suppose that 238U can only burn out and cannot accumulate in any way. Then its kinetic equation is
 (7)
(7)
Using the same dimensionless densities and coordinates one obtains:
 (8)
(8)
239U is produced during the neutron capture by 238U. Its amount decreases due to absorption of neutrons (neutron capture or nuclear fission) and β-decay with characteristic time τβ. So the equation for 239U is
 (9)
(9)
After scaling, the equation (9) takes the form:
 (10)
(10)
Since 239Pu is produced by the β-decay of 239 U, and burns out absorbing neutrons, the kinetic equation for 239Pu is
 (11)
(11)
After simplification and combining together with equations (5) (8) and (10) one can obtain the next system of equations:
![\begin{eqnarray*} \begin{cases} \frac{\partial n}{\partial t}\left( t,y \right)=\frac{{{\partial }^{2}}n}{\partial {{y}^{2}}}\left( t,y \right)\\[4pt] \quad+\left( \left( \nu -2 \right){{n}_{\textrm{Pu}}}\left( t,y \right)-{{n}_{8}}\left( t,y \right)-{{n}_{9}}\left( t,y \right) \right)n\left( t,y \right), \\[4pt] \frac{\partial {{n}_{8}}\left( t,y \right)}{\partial t}=- {{n}_{8}}\left( t,y \right)n\left( t,y\right), \\[4pt] \frac{\partial {{n}_{9}}\left( t,y \right)}{\partial t}=\left( {{n}_{8}}\left( t,y \right)-{{n}_{9}}\left( t,y \right) \right)n\left( t,y \right)-\frac{\tau }{{{\tau }_{\beta }}}{{n}_{9}}\left( t,y \right), \\[4pt] \frac{\partial {{n}_{\textrm{Pu}}}\left( t,y \right)}{\partial t}=\frac{\tau }{{{\tau }_{\beta }}}{{n}_{9}}\left( t,y \right)-\frac{1}{{{{\tilde{n}}}_{\textrm{Pu}}}}{{n}_{\textrm{Pu}}}\left( t,y \right)n\left( t,y \right) \\ \end{cases}\end{eqnarray*}](/articles/epjn/full_html/2020/01/epjn190055/epjn190055-eq18.png) (12)
(12)
System (12) is almost the same as in [8], but in the diffusion equation we use explicitly the contribution of the combustion of fuel (namely 238U and 239U).
As one can see, a very small parameter  emerged in the problem – the ratio of the neutron mean free time τ (about 10−7 s) to the characteristic time of β-decay τβ ≈ 3.3 days. We shall denote this parameter as:
emerged in the problem – the ratio of the neutron mean free time τ (about 10−7 s) to the characteristic time of β-decay τβ ≈ 3.3 days. We shall denote this parameter as:
![\begin{equation*} \varepsilon \equiv \frac {\tau} {{\tau} _{\beta}} \approx 10^{-14} [\textrm{s}].\end{equation*}](/articles/epjn/full_html/2020/01/epjn190055/epjn190055-eq21.png) (14)
(14)
Let us convert the resulting system of kinetic equations into the autowave form. For this purpose, we make the variable substitution according to the relation z = y + ut. With such substitution, the burning wave goes in the negative direction of the coordinate axis of the autowave variable z. The derivatives change as follows:

System (12) in autowave form reads
![\begin{eqnarray*} \begin{cases} u\frac{{dn}}{{dz}}\left( z \right) = \frac{{{d^2}n}}{{d{z^2}}}\left( z \right) \\[4pt] \quad+ \left( {\left( {\nu - 2} \right){n_{\textrm{Pu}}}\left( z \right) - {n_8}\left( z \right) - {n_9}\left( z \right)} \right)n\left( z \right),\\[4pt] u\frac{{d{n_8}\left( z \right)}}{{dz}} = - {n_8}\left( z \right)n\left( z \right),\\[4pt] u\frac{{d{n_9}\left( z \right)}}{{dz}} = \left( {{n_8}\left( z \right) - {n_9}\left( z \right)} \right)n\left( z \right) - \varepsilon {n_9}\left( z \right),\\[4pt] u\frac{{d{n_{\textrm{Pu}}}\left( z \right)}}{{dz}} = \varepsilon {n_9}\left( z \right) - \frac{1}{{{{\tilde n}_{\textrm{Pu}}}}}{n_{\textrm{Pu}}}\left( z \right)n\left( z \right). \end{cases}\end{eqnarray*}](/articles/epjn/full_html/2020/01/epjn190055/epjn190055-eq23.png) (17)
(17)
The second equation in system (17) may be integrated. Than we obtain the following expression for the 238U concentration:
 (18)
(18)
where n8,−∞ is the 238U concentration when  . Since we use the values scaled to theinitial 238U concentration, n8,−∞ = 1.
. Since we use the values scaled to theinitial 238U concentration, n8,−∞ = 1.
Applying the variable substitution and some basic mathematical transformations, one can integrate the rest of the equations from (17). The system of equations then takes the form:
 (19)
(19)
Let us consider the last equation of the system (19) in more detail. We then direct argument to plus infinity in this expression, i.e.  . Then, we have the following:
. Then, we have the following:
 (20)
(20)
This expression may be conventionally split into three multipliers: the constant  , the exponent, and the integral. The integrand is the exponent multiplied by 239U concentration, and the interval of integration is from
, the exponent, and the integral. The integrand is the exponent multiplied by 239U concentration, and the interval of integration is from  to
to  . The exponent is strictly more than zero throughout the entire integration interval (the properties of this function). The 239U concentration is a non-negative value, and it has to be greater than zero at some points because otherwise there would be no reaction andno wave of nuclear burning at all. So the integral is of the product of two positive functions, and consequently, is also a positive quantity which is certainly not equal to zero. Since the constant (the quotient of two positive values) and the exponent (property of the function) are also positive values, then the entire product is certainly more than zero. Thus it may be concluded that the plutonium cannot burn out completely. Instead, it tends to some constant level:
. The exponent is strictly more than zero throughout the entire integration interval (the properties of this function). The 239U concentration is a non-negative value, and it has to be greater than zero at some points because otherwise there would be no reaction andno wave of nuclear burning at all. So the integral is of the product of two positive functions, and consequently, is also a positive quantity which is certainly not equal to zero. Since the constant (the quotient of two positive values) and the exponent (property of the function) are also positive values, then the entire product is certainly more than zero. Thus it may be concluded that the plutonium cannot burn out completely. Instead, it tends to some constant level:  . This is also confirmed by the results of numerical simulation of the burning kinetics, e.g. [14,15]. The fact, that plutonium can not completely burn out indicates, that in the active zone of traveling-wave nuclear burning the reproduction coefficient is greater than unity, which the boundary condition
. This is also confirmed by the results of numerical simulation of the burning kinetics, e.g. [14,15]. The fact, that plutonium can not completely burn out indicates, that in the active zone of traveling-wave nuclear burning the reproduction coefficient is greater than unity, which the boundary condition  is corresponds to.
is corresponds to.
Let us assume the following:
 (21)
(21)
Applying the approximation (21), we proceeded with the following considerations. The integral in (21) is  . If we substitute the function
. If we substitute the function  under the integral by its value at the upper limit
under the integral by its value at the upper limit  , then for the points z2 near the upper limit of integration, such substitution it is possible because of the approximate equality
, then for the points z2 near the upper limit of integration, such substitution it is possible because of the approximate equality  for the small deviation of z2 from z. On the other hand, for the points far from the upper limit of integration such substitution becomes possible due to the fact that
for the small deviation of z2 from z. On the other hand, for the points far from the upper limit of integration such substitution becomes possible due to the fact that  for z2 ≪z. So the concentration
for z2 ≪z. So the concentration  in this case will enter the integral with a coefficient that is exponentially small in comparison with that of n(z). Therefore, one can expect that the value of the integral will be much less sensitive to the accuracy of the approximation in the region z2 ≪z as compared to the region, where z2 is close to z, where the approximation
in this case will enter the integral with a coefficient that is exponentially small in comparison with that of n(z). Therefore, one can expect that the value of the integral will be much less sensitive to the accuracy of the approximation in the region z2 ≪z as compared to the region, where z2 is close to z, where the approximation  should be a good one.
should be a good one.
With this approximation, the system of equations (19) will take the form:
![\begin{eqnarray*} \begin{cases} \frac{1}{u}\frac{{dn}}{{dz}}\left( z \right) = n\left( z \right) - {n_9}\left( z \right)+ \left( {\nu - 2} \right){{\tilde n}_{\textrm{Pu}}}{n_{\textrm{Pu}}}\left( z \right) \\ \quad- \frac{\varepsilon }{u}\left( {1 + \left( {\nu - 2} \right){{\tilde n}_{\textrm{Pu}}}} \right)\int\limits_{ - \infty }^z {{n_9}\left( {{z_1}} \right)d{z_1}}\\ \quad + 2\left( {1 - \exp \left( { - \frac{1}{u}\int\limits_{ - \infty }^z {n\left( {{z_1}} \right)d{z_1}} } \right)} \right),\\ {n_8}\left( z \right) = \exp \left( { - \frac{1}{u}\int\limits_{ - \infty }^z {n\left( {{z_1}} \right)d{z_1}} } \right),\\ {n_9}\left( z \right) = \frac{1}{\varepsilon }\exp \left( { - \frac{1}{u}\int\limits_{ - \infty }^z {n\left( {{z_1}} \right)} d{z_1}} \right)n\left( z \right),\\ {n_{\textrm{Pu}}}\left( z \right) = \frac{{{\tilde n}_{\textrm{Pu}}}}{{1 - {{\tilde n}_{\textrm{Pu}}}}} \Bigg[ \exp \left( { - \frac{1}{u}\int\limits_{ - \infty }^z {n\left( {{z_1}} \right)} d{z_1}} \right) \\ \quad - \exp \left( { - \frac{1}{{u{{\tilde n}_{\textrm{Pu}}}}}\int\limits_{ - \infty }^z {n\left( {{z_1}} \right)d{z_1}} } \right) \Bigg]. \end{cases}\end{eqnarray*}](/articles/epjn/full_html/2020/01/epjn190055/epjn190055-eq43.png) (22)
(22)
Since the burning wave is propagating in a negative direction, the boundary conditions are set at minus infinity and have the following form:
 (23)
(23)
where n8,−∞ is the initial 238U concentration.
3 The analogy to Newton’s second law
Let us consider the first equation of the system (22). As we have already derived the expressions for 239U and 239 Pu from other equations, we can substitute them here. After substitution we can collect terms and integrate some parts of this equation. Finally we obtain the following expression:
![\begin{eqnarray*} &&\hskip-16pt \frac{1}{u}\frac{{dn}}{{dz}}\left( z \right) = \left[ {1 - \frac{1}{\varepsilon }\exp \left( { - \frac{1}{u}\int\limits_{ - \infty }^z {n\left( {{z_1}} \right)} d{z_1}} \right)} \right]n\left( z \right) \nonumber\\ &&\hskip18pt + \left( {1 - \left( {\nu - 2} \right){{\tilde n}_{\textrm{Pu}}}} \right)\nonumber\\ &&\hskip18pt + \frac{{(\nu -1) {{\tilde n}_{\textrm{Pu}}} - 1}}{{1 - {{\tilde n}_{\textrm{Pu}}}}}\exp \left( { - \frac{1}{u}\int\limits_{ - \infty }^z {n\left( {{z_1}} \right)} d{z_1}} \right) \nonumber\\ &&\hskip18pt -\frac{{\left( {\nu - 2} \right){{\left( {{{\tilde n}_{\textrm{Pu}}}} \right)}^2}}}{{1 - {{\tilde n}_{\textrm{Pu}}}}}\exp \left( { - \frac{1}{{u{{\tilde n}_{\textrm{Pu}}}}}\int\limits_{ - \infty }^z {n\left( {{z_1}} \right)d{z_1}} } \right)\!\!.~~~\end{eqnarray*}](/articles/epjn/full_html/2020/01/epjn190055/epjn190055-eq45.png) (24)
(24)
So we got integro-differential equation. Let us introduce a new variable N(z) into it, as follows:
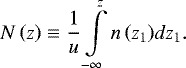 (25)
(25)
The physical meaning of this value is neutron fluence divided by the wave velocity or called neutron density accumulation over time. Let us treat N(z) as an analog of coordinate. Note that the speed, i.e. a derivative of this coordinate, cannot be negative. In our case the derivative is a neutron concentration, thus a negative sign at the speed means the same sign at n(z), which takes us out of the physical region.
Taking into account (25), (24) becomes
 (26)
(26)
Let us note that equation (26) looks like this because we did not neglect the derivative over time in the system of kinetic equations, when switching to the autowave variable z = y + ut in Section 2, as it was done e.g. in [1,3,5,11,16,17].
One could draw a parallel between equation (26) and Newton’s second law. If we consider the N(z) an analog to coordinate, its second derivative is the acceleration. So one has a resultant force scaled to mass on the left in equation (26). On the right, there is a sum of a viscous force (a term including velocity) and a force caused by some potential of interaction (which is a gradient of potential energy with a negative sign). It is easy to build an expression, the negative derivative of which would coincide with this term and which can be regarded as an analog to the potential energy. One can easily obtain the equation (26) in the form:
 (27)
(27)
A derivative of the sum of kinetic and potential energy in the expression (27) equals to the viscous force. Thus this equation may be considered as the energy conservation law, and the total energy may change only through the work of the viscous force.
We are interested in finding cases of equilibrium, which corresponds to the autowave fission mode. This happens when the total force consisting of the “potential” force and “dissipative” viscous force, is zero. For this, the potential energy must have a point of minimum, because the derivative (the potential force) is zero at this point. The speed (and hence the kinetic energy) must also be zero at this minimum point, meaning the dissipative viscous force is zero. Analyzing different values of coefficients k1, k2 and k3 depending on the ñPu parameter, we found that in order to obtain the potential energy (28) with a minimum point, it is enough that the ñPu > 1. If this condition is satisfied, than the potential energy has a form, as shown in Figure 1. There is an apparent point of minimum in this graph – a stable stationary point. The derivative of potential energy (the potential force) is obviously zero at this point. So this is a possible stationary state, if the kinetic energy is zero, and corresponds to the autowave fission mode.
Remind that the derivative of N cannot be negative, because it would lead us to negative neutron concentration, which is non-physical. If we treat N as an analog of some coordinate, then its derivative is the speed. So this speed cannot be negative – as non-physical. If the object starts from the point N = 0 and we want it to stop at the point of equilibrium (minimum), it should not overshoot this point. Otherwise the derivative of the potential energy will be non-zero, the force will act on the body, and the body will keep moving. It is known that the potential energy cannot be greater than total energy, so at some moment, when the kinetic energy completely transforms into potential, the object will start moving in the opposite direction. This means that the speed of the body will become negative. And we cannot allow this as non-physical. Therefore it is necessary for the entire kinetic energy to dissipate due to viscosity by the time when the potential energy reaches a point of minimum. This way point the object stops at a stationary point. Graphically this path is shown by the arrow in Figure 1.
As ñPu and ν (via Eqs. (13) and (43), respectively) depend on the neutrons energy, in the Section 5 we will find all possible energy values, at which the potential function has a minimum point.
 |
Fig. 1 A single possible form of potential energy that allows the existence of an auto-wave mode is shown in black. The arrow showsthe path of total energy along which this mode can be set. |
4 Finding a criterion for the wave velocity
We determined that for the autowave mode to be possible, the coefficients k1, k2 and k3 (taking into account the value ñPu) must be chosen in such a way, that the potential energy (or its analog) has a point of minimum. The potential force (the derivative of U(N) with opposite sign) in this case, will look like it is shown in Figure 2 (solid line).
Since in the autowave form the wave propagates over an infinite interval, and there is no explicit dependence on variable z in equation (27), it is always possible to perform a variable substitution that shifts z relative to the function N. Let us thus switch to a new variable so that z = 0 at the point  . We replace the function of force by a triangular one (dashed line in Fig. 2).
. We replace the function of force by a triangular one (dashed line in Fig. 2).
Next, we try to replace the function of force with two straight lines – one on the negative part of the coordinate axis z, and the other on the positive part. If we solve the equation (27) for N with the functions of force in the form of two lines, we obtain two unknown constants for each one of solutions (because the equations are of second-order). We adjust these constants to satisfy the boundary conditions. We also hope that the constants adjustment will end up with zeroing out one of them for each solution since the functions at which they appear will diverge to infinity. Then, if we join the functions and their first derivatives at the point  , we would obtain one spare equation, which can be used to find the wave speed.
, we would obtain one spare equation, which can be used to find the wave speed.
So, let us first consider the interval  . Here we make the following substitution:
. Here we make the following substitution:

where q is the slope, and is equal to:
 (32)
(32)
By substituting (31) into (27) we obtain a homogeneous differential equation of second order, whose solution looks like:

χ1 is apparently positive, and χ2 is negative. So in order for the N(z) to converge to (−∞), C2 must be zero. So
 (35)
(35)
Now let us consider the interval 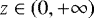 . In this case we make the following substitution:
. In this case we make the following substitution:

If we substitute the potential energy again into (27), we obtain a similar solution.
 (38)
(38)
![\begin{eqnarray*} {\lambda _{1,2}} &=& \frac{1}{2}\Bigg[ - u\frac{{{n_{8, - \infty }}}}{\varepsilon }\exp \left( { - {N_0}} \right) \nonumber\\ && \pm \sqrt {{{\left( {\frac{{u{n_{8, - \infty }}}}{\varepsilon }\exp \left( { - {N_0}} \right)} \right)}^2} - 4} \Bigg].\end{eqnarray*}](/articles/epjn/full_html/2020/01/epjn190055/epjn190055-eq66.png) (39)
(39)
As we can see, both λ1 and λ2 are negative, so at (+∞) both constants are at the “good” exponents (the converging ones), and we cannot zero out any of them. So this way we do not obtain an additional equation, which could be used to find the wave speed.
There is an expression that may be negative under the root in equation (39). Thus, the solution will be the sum of sine and cosine with some coefficients. Since they have a finite period, and the wave propagates on an infinite interval, the derivative will become negative at some point. As we noted above, this would lead us to the negative neutron concentration, which is non-physical. So we require that
 (40)
(40)
Considering this requirement relative to u, we obtain the following restriction:
 (41)
(41)
It means, that the wave velocity may take a continuous spectrum of values greater than a certain minimum value. In the framework of the analogy to the energy conservation law, one might say that the viscosity cannot be less than a certain value. It makes sense, because with higher viscosity the kinetic energy will still dissipate completely to the minimum point, but if the viscosity is not high enough, the body will possess some nonzero speed at the stationary point, which eventually leads to the reverse motion. And as we noted above, the reverse motion is not allowed as non-physical.
Let us check if the speed can take different values. To do this, we choose the parameters so that the potential energy has the point of minimum, and solve the equation (26) numerically. These parameters are: ñPu = 0.74, ν = 2.8, N0 = 1.8, where N0 is the point of potential energy minimum. With such values, the condition (41) has the form: u ≥ 15ε. Figure 3 shows the dependences of N on z for different velocities. Comparing it to the potential energy (Fig. 1a), one cannot notice the following: the coordinate is initially zero, and then it goes to the point of the potential energy minimum. The change in speed, i.e. dissipative force, affects the form of this transition and shifts it in time.
 |
Fig. 2 A solid line shows a schematic representation of the potential force F(N) (a derivative of U(N) taken withthe opposite sign), when the potential energy has a minimum point (the type of potential from Fig. 1c). A dashed line shows an approximate force which we use in our work for while looking for the wave velocity criterion. |
 |
Fig. 3 Solutions of equation (26) as a function N(z) when a minimum exists in potential energy. The curves are given for different velocities that satisfy the requirement (41). |
5 The spectrum of neutron energies, suitable for an auto-wave mode
In order to make possible the existence of the traveling-wave mode, the potential energy (or its analog) must have a point of minimum, and also the wave speed must be such that the kinetic energy is completely dissipated when the potential energy reaches this minimum point. So now as we realize that, it is interesting to study how the fulfillment of the first condition (existence of the minimum point) depends on the neutrons energy. According to (29) and (28), U(N) depends on ν and ñPu. These parameters, in turn, depend on the neutron energy. We find the parameter ñPu using equation (13) and examine it depending on the neutron energies.
According to [18–20], the mean number of instantaneous neutrons ν produced bysingle fission has the following dependence on energy:
 (42)
(42)
Since we are interested in the average number of neutrons ν for Pu239, we choose the following parameters for the equation (42):
 (43)
(43)
So now we know the dependence of the coefficients in the potential energy on the energy of the neutrons. We have to find the entire spectrum of neutron energies at which the potential energy has a point of minimum. It may be done as follows. Break some interval of N (from zero up to a certain maximum value) into sufficiently small segments, and compare the values of U(N) at three adjacent points. If the value at the middle point is less than those at both ends, then the minimum of the function exists. If we do not find such three points, then there is no minimum at this energy. Having analyzed the entire spectrum of neutron energies for which it was possible to find a cross-section values in [21], that is from 0 to 15 MeV this way, we find all the energy intervals with minima.
We show all the neutron energies, for which we found the minimum of potential energy, as a set of points in the graph, where the neutron energy is along the X-axis and the parameter ñPu is along the Y -axis. Only the values, for which there is a stationary point in the potential energy, are shown.
Figure 4 shows the values of the parameter ñPu for neutron energies in the range from 0 to 100 eV. We used the dependence of the cross-sections of nuclides on the neutron energy from the database [21]. As seen from Figure 4 (according to the considerations in Sect. 3), there are seven regions at about 6–7 eV, 19–21 eV, 34–40 eV, 66–67 eV, 81–82 eV and 90–100 eV, having a minimum of potential energy, which makes the autowave of nuclear fission possible. The spectrum of ñPu values, where the minimum of potential energy was found, looking among the all the neutron energies which were available in [21] (from 0 to 15 [MeV]) is shown in Figure 5.
It is worth mentioning, that results described in Figure 5 for fast neutrons region have a preliminary nature. This is due to the fact the calculating with one-group approximation admits a significant error in the fast neutron spectrum. Therefore it is necessary to use the multigroup approximation for quantitative calculations.
For all the previous considerations we assumed that in equation (27) the right-hand side is always negative. We did it as the dominant negative term in the brackets is proportional to  . Nevertheless if N(z) is large enough, than the exponent can make the term very small and the total viscous force will become positive, what is difficult to interpret within our Newton’s law analogy. As we are interested in a potential of Figure 1 - kind, than the maximum possible value of N(z) is a N0. If in that point the viscous force in equation (27) is still zero, than all are speculations above are valid. So we checked the value of the coefficient
. Nevertheless if N(z) is large enough, than the exponent can make the term very small and the total viscous force will become positive, what is difficult to interpret within our Newton’s law analogy. As we are interested in a potential of Figure 1 - kind, than the maximum possible value of N(z) is a N0. If in that point the viscous force in equation (27) is still zero, than all are speculations above are valid. So we checked the value of the coefficient  for the different energies of neutrons, but requiring that the potential equation (28) has a minimum point and N0 is this point ofminimum. The values of this factor are shown at Figure 6 and one can see that all of them are much greater than zero, what means that viscous force in equation (27) takes always only the negative values.
for the different energies of neutrons, but requiring that the potential equation (28) has a minimum point and N0 is this point ofminimum. The values of this factor are shown at Figure 6 and one can see that all of them are much greater than zero, what means that viscous force in equation (27) takes always only the negative values.
 |
Fig. 4 The dependence of the parameter ñPu on the energy of neutrons, for the energies, when the potential energy has the point of minimum, and the autowave may exist. The image shows the energy range from 0 to 105 eV. |
 |
Fig. 5 The dependence of the parameter ñPu on the energy of neutrons, for the energies, when the potential energy has the point of minimum, and the existence of an autowave is possible. This picture embraces all possible points, as the entire region of neutron energies, where it was possible to obtain an experimental data for the cross-sections [21]. Namely, the energy range is (0, 15) MeV. |
 |
Fig. 6 Coefficient at the viscous force equation (27) taken at the point of Potential energy minimum as a function of the energy of neutrons, where there is a minimum point. |
6 Numerical solution of the non-stationary system of equations
To confirm the conclusions of the theoretical model, by the numerical simulation we selected the epithermal region of neutrons energy. Also, we will try to confirm the relation between automodel regime existence and the form of potential energy analog. As follows fromFigure 5, the form of potential energy analog in this region (about 5.9 eV) is appropriate for the automodel regime’s existence. Note, that research of autowave nuclear burning regime existence is the foreground for authors of this article. e.g. [13].
The system of equations studied above is simplified and does not fully reflect the physical processes that take place in the reactor core.Let us consider the system of equations given in [13], which is more accurate (though not ideal), and consists of 18 equations. The kinetic equation for the neutron concentration
 (44)
(44)
where q(y, t) is the internal source of neutrons, which has the form:
![\begin{eqnarray*} q\left( {y,t} \right) &=& \left[ {{\nu ^{\textrm{Pu}}}\left( {1 - {p^{\textrm{Pu}}}} \right) - 1} \right] n\left( {y,t} \right) {V_n} \sigma _f^{\left( \textrm{Pu} \right)} {N_{\textrm{Pu}}}(y,t) \nonumber\\ &&+ \left[ {{\nu ^{5}}\left( {1 - {p^{5}}} \right) - 1} \right] n(y,t) {V_n} \sigma _f^{\left( 5 \right)} {N_5}(y,t)\nonumber \\ &&+ \ln 2 \sum\limits_{i = 1}^6 {\left[ {\frac{{\tilde N_i^{\left( {\textrm{Pu}} \right)}(y,t)}}{{T_i^{\left( {\textrm{Pu}} \right)}}} + \frac{{\tilde N_i^{\left( 5 \right)}(y,t)}}{{T_i^{\left( 5 \right)}}}} \right]}\nonumber \\ && - n(y,t) {V_n} \sum\limits_{5,8,9,Pu} {\sigma _c^{\left( i \right)} {N_i}(y,t)} \nonumber\\ &&\hskip-9pt - n(y,t) {V_n} \sum\limits_{i = 1}^6 {\left[ {\sigma _c^{i\left( {\textrm{Pu}} \right)} \tilde N_i^{\left( {\textrm{Pu}} \right)}(y,t) + \sigma _c^{i\left( 5 \right)} \tilde N_i^{\left( 5 \right)}(y,t)} \right]} \nonumber \\ &&- n(y,t) {V_n} \sigma _c^{\textrm{eff}\left( {\textrm{Pu}} \right)} {{\bar N}^{\left( {\textrm{Pu}} \right)}}(y,t) \nonumber\\ && - n(y,t) {V_n} \sigma _c^{\textrm{eff}\left( 5 \right)} {{\bar N}^{\left( 5 \right)}}(y,t).\end{eqnarray*}](/articles/epjn/full_html/2020/01/epjn190055/epjn190055-eq76.png) (45)
(45)
In equations (44) and (45) n(y, t) is the neutron concentration; Vn is the neutron velocity; νPu and ν5 are the mean number of instantaneous neutrons per 239Pu and 235U fission respectively.N5, N8, N9 and NPu are the 235U, 238U, 239U and 235 Pu concentrations respectively;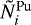 and
and  are the concentrations of fragments with neutron excess, produced due to 239 Pu and 235U fission respectively;
are the concentrations of fragments with neutron excess, produced due to 239 Pu and 235U fission respectively; and
and  are the concentrations of all the other fission fragments of 239Pu and 235U respectively;σc and σf are the microscopic cross-sections of the neutron capture and nuclear fission; the parameters pi
are the concentrations of all the other fission fragments of 239Pu and 235U respectively;σc and σf are the microscopic cross-sections of the neutron capture and nuclear fission; the parameters pi  and T1∕2 characterizethe groups of delayed neutrons. They are well known and presented in [20].
and T1∕2 characterizethe groups of delayed neutrons. They are well known and presented in [20].  is some effective microscopic cross-section of neutron capture by fragments.
is some effective microscopic cross-section of neutron capture by fragments.
One can find the whole set of kinetic equations, together with the constants used there in [13]. We use here dimensionless concentrations and coordinates, normalized in the same way as we did for the simplified system of equations. Now we assume, that initial medium consists not only from the 238U, but also from 238U and initial conditions are:
 (46)
(46)
where η8 and η5 are constants adjusting the fuel enrichment (η8 + η5 = 1). The remaining elements are initially absent.
In contrast to [8,13] we want to find the traveling-wave mode, so when there are no external neutrons come to the system and it burns in itself. In order to obtain it, we want firstly to switch the external neutron flux on and then, after some time, switch it off. We want to check if the system can set up the equilibrium with a soliton-like burning wave. The initial and boundary conditions for neutrons we set as
 (47)
(47)
where  is some function specifying the number of external neutrons and which satisfies our statements above.
is some function specifying the number of external neutrons and which satisfies our statements above.
For the numerical simulation, we use Wolfram Mathematica. We perform the calculations for the energy of neutrons En = 5.923 (eV). During the manipulation with a full system of equations we obtain a similar parameter as in equation (14). Unfortunately, at this stagewe cannot solve the system with a real value of this parameter, so let us take some approximation. We take ε = 10−3. This value is not realistic (ε is about 10−14), but it is difficult to carry out the numerical calculations with more precise values for our model.
We want to set the function n0(t) in such a way that the external neutrons flux will be switched on for some time and then it drops to zero. In particular, we set the dependence of the boundary neutrons density on the time as it is in the equation (48). With such a function the neutrons come only for a time period around t =10 (in our dimensionless units) and then it goes to zero. As we want to see the setting of the autowave, we will show the results which are much beyond the time of switching off a source and out plots starts from t =105.
 (48)
(48)
Figures 7–10 present the results of numerical simulation (with the neutron energy En = 5.923 (eV)) with the external source of neutrons being switched off already. In Figures 7–10 are presented the concentrations of neutrons, 238U, 239U and 239 Pu, respectively.The setting of the autowave mode of nuclear burning is confirmed by the fact that starting from a certain moment in time (when the external source of neutrons is already switched off), each subsequent curve differs from the previous only by a shift along the y-axis.
We also studied the regions of neutron energies for which there was no minimum in potential energy. In such cases, the autowave mode did not establish, and the wave faded away after the external source of neutrons was switched off.
The results of numerical modeling confirm the obtained theoretical conclusions. According to these results, one of the possible areas of autowave burning in the uranium-plutonium medium is the epithermal region of neutron energies (as in [13,22]). Meanwhile in the region of fast neutrons, the wave burning of the uranium-plutonium medium requires the constant supply of neutrons from an external source and the wave fades out when the source is switched off.
The discovered burning mode with external support can be used for implementing a traveling-wave reactor, e.g. to stop the burning at any time by switching off the external source of neutrons.
 |
Fig. 7 The concentrations of neutrons as a function of the spatial coordinate y in the different moments of time (from t = 200 000 to t = 1 000 000) obtained from the numerical solution. The different lines correspond to the particular moments of time. |
7 Conclusions
A kinetic system of equations, describing the wave mode of neutron-nuclear burning in the uranium-plutonium medium is formulated. Its autowave form is also obtained. In contrast to many other papers like [1,3,5,11,16,17], in which it was also considered in autowave form, we do not neglect the derivative of neutron concentration with respect to time in the neutron diffusion equation. This way we study the non-stationary traveling-wave burning mode.
For the first time, a kinetic equation for neutrons is obtained in the form of the energy conservation law for a mechanical system withdissipation, and the mechanical analogy for the fission traveling wave is developed. This allowed us to formulate the conditions for the existence of the autowave burning mode, and determine the possible values of the wave speed. The values of the burning wave rates have a continuous distribution and are bounded at the bottom, that is, they have a continuous spectrum. We also succeeded in determining the regions of neutron energy, for which the autowave burning is possible. We conclude that in other energy ranges, in which the autowave mode is impossible, the wave of nuclear burning may still be established using the support of an external neutron source. It should be noted, that these results are preliminary and further refinement is planned with the aid of more accurate calculations.
To confirm the theoretical conclusions, we performed a numerical 1D simulation of the neutron-nuclear burning in the uranium-plutonium medium in a single-group diffusion approximation (En = 5.923 (eV)). The results of numerical modeling confirm the obtained theoretical conclusions. According to these results, one of the possible areas of autowave burning in the uranium-plutonium medium is the epithermal region of neutron energies (as in [13,22]).
We regarded a significantly simplified model in the paper. Nevertheless, obtained results can be used as a first approximation in more realistic models. In particular, we did not count the energy distribution of neutrons and cross-sections (as it was done in [2]), but the limiting stage of the investigated processes was a β-decay, which does not depend on the energy of the neutrons. If one will use a multigroup approximation (as in [2]), then different groups of neutrons will have their typical times for the processes which happen to them. So during the problem solution, these times will be included as the ratios between them and their ratio to the typical β-decay time. Despite its small value, the ratio to the β-decay cannot be neglected as setting it to zero leads to the loosing of the neutrons multiplication channel and consequently, the traveling-wave solution is lost. Therefore, one cannot get the autowave iteratively, starting from an approximation, when all of them are equal to zero. But, as we showed in the work, one can obtain a traveling-wave solution putting them all equal to each other. Similar speculations can be applied to the ratios of typical neutrons times to each other. Putting them all equal to one, we get an initial solution for the iterative procedure. Having the wave at first approximation, it is possible to move on and count the multigroup effects by sequential iterations for discussed parameters. The fact that the β-decay plays a crucial role in the wave formation and it does not depend on the energy of the neutrons, allows us to expect that such an iterative approach will change a form and speed of the wave, but will not ruin the autowave solution.
One more approximation is that we work one the one-dimensional system within plane geometry. The possible improvement can be performed in a way as in [9,11], that is solving a system for a wave spreading in a cylindrical tube. In a diffusional approximation, the boundary conditions represent the continuity of the neutrons flux that is a continuity of the radial component of the gradient. It is possible to regard an ideally reflective or ideally absorbing tube walls, and neutrons will not be able to get inside the walls. In such a case the radial flux will be equal to zero, so this is a requirement for the boundary conditions. Such a requirement is also satisfied by the particular solution when the radial component is zero along all the tube surface. In that case, the problem is reduced to the one, regarded in the present work. So it is possible to take our results as a first approximation and move towards more realistic problems.
Author contribution statement
V. Urbanevych: performed analytical derivation of the model and numerical calculations in order to prove it. Prepared the figures and wrote the manuscript draft. I.V. Sharph: conceived of the model, supervised the work. V.A. Tarasov: co-supervised the work, worked on the text of the article. V.D. Rusov: discussions about the model, useful pieces of advice to improve the model. All authors put their efforts in order to obtain the final version of the article.
References
- L. Feoktistov, Rep. Acad. Sci. USSR 309, 864 (1989) [Google Scholar]
- H. Sekimoto et al., Nucl. Sci. Eng. 139, 306 (2001) [CrossRef] [Google Scholar]
- H. van Dam, Ann. Nucl. Energy 27, 1505 (2000) [CrossRef] [Google Scholar]
- A.P. Ershov, V.F. Anisichkin, Combust. Explos. Shock Waves 39, 226 (2003) [CrossRef] [Google Scholar]
- X.-N. Chen et al., Energy Convers. Manage. 59, 40 (2012) [CrossRef] [Google Scholar]
- V.V. Gann, A.V. Gann, NPAE-Kyiv2012 Proceedings (2012) [Google Scholar]
- N.G. Kodochigov, Y. Sukharev, presented at 7th International Topical Meeting on High Temperature Reactor Technology: The modular HTR is advancing towards reality, Tsinghua University, China, 2014 [Google Scholar]
- K. Anoop, O. Singh, Sadhana 43, (2018) [Google Scholar]
- X.-N. Chen, W. Maschek, J. Hydrodyn. Ser. B 18, 49 (2006) [CrossRef] [Google Scholar]
- L. Feoktistov, Successes of physics sciences 163, 89 (1993) [Google Scholar]
- X.-N. Chen, E. Kiefhaber, Energies 8, 13829 (2015) [CrossRef] [Google Scholar]
- A. Volpert, V. Volpert, Nonlinear Anal. 49, 113 (2002) [CrossRef] [Google Scholar]
- V.D. Rusov et al. Prog. Nucl. Energy 83, 105 (2015) [CrossRef] [Google Scholar]
- V.D. Rusov et al. J. Geophys. Res. 112, B09203 (2005) [Google Scholar]
- V.D. Rusov et al., Sci. Technol. Nucl. Install. 2015, 1 (2015) [CrossRef] [Google Scholar]
- V.N. Pavlovich et al., At. Energ. 102, 181 (2007) [CrossRef] [Google Scholar]
- V.M. Khotyayintsev et al., Ann. Nucl. Energy 85, 337 (2015) [CrossRef] [Google Scholar]
- A. Weinberg, E. Wigner, The Physical Theory of Neutron Chain Reactors. (The University of Chicago Press, Chicago, 1958) [Google Scholar]
- V.M. Pavlovych, Physics of nuclear reactors (Nuclear station security and safety problem research institute, Chernobyl, 2009) [Google Scholar]
- G. Bartolomey et al., Basic Theory and Methods of Nuclear Power Installations Calculation (Energoatomizdat, Moscow, 1989) [Google Scholar]
- M. Chadwick et al., Nucl. Data Sheets 112, 2887 (2011) [CrossRef] [Google Scholar]
- V.A. Tarasov et al., Nuclear reactor on a traveling wave: ultra-slow wave neutron-nuclear combustion on epithermal neutrons and regimes with peaking in a uranium-plutonium fission medium (Publishing group “A.C.C.”, Kyiv, 2016) [Google Scholar]
Cite this article as: Vitalii Urbanevych, Igor Sharph, Viktor Tarasov, Vitaliy Rusov, Newton's second law analogy for the traveling wave of nuclear burning, EPJ Nuclear Sci. Technol. 6, 50 (2020)
All Figures
 |
Fig. 1 A single possible form of potential energy that allows the existence of an auto-wave mode is shown in black. The arrow showsthe path of total energy along which this mode can be set. |
| In the text | |
 |
Fig. 2 A solid line shows a schematic representation of the potential force F(N) (a derivative of U(N) taken withthe opposite sign), when the potential energy has a minimum point (the type of potential from Fig. 1c). A dashed line shows an approximate force which we use in our work for while looking for the wave velocity criterion. |
| In the text | |
 |
Fig. 3 Solutions of equation (26) as a function N(z) when a minimum exists in potential energy. The curves are given for different velocities that satisfy the requirement (41). |
| In the text | |
 |
Fig. 4 The dependence of the parameter ñPu on the energy of neutrons, for the energies, when the potential energy has the point of minimum, and the autowave may exist. The image shows the energy range from 0 to 105 eV. |
| In the text | |
 |
Fig. 5 The dependence of the parameter ñPu on the energy of neutrons, for the energies, when the potential energy has the point of minimum, and the existence of an autowave is possible. This picture embraces all possible points, as the entire region of neutron energies, where it was possible to obtain an experimental data for the cross-sections [21]. Namely, the energy range is (0, 15) MeV. |
| In the text | |
 |
Fig. 6 Coefficient at the viscous force equation (27) taken at the point of Potential energy minimum as a function of the energy of neutrons, where there is a minimum point. |
| In the text | |
 |
Fig. 7 The concentrations of neutrons as a function of the spatial coordinate y in the different moments of time (from t = 200 000 to t = 1 000 000) obtained from the numerical solution. The different lines correspond to the particular moments of time. |
| In the text | |
 |
Fig. 8 The same as in Figure 7 but for the concentration of the 238U. |
| In the text | |
 |
Fig. 9 The same as in Figure 7 but for the concentration of the 239U. |
| In the text | |
 |
Fig. 10 The same as in Figure 7 but for the concentration of the 239Pu. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





