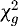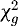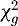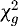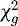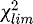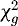| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
|
|
|---|---|---|
| Article Number | 26 | |
| Number of page(s) | 7 | |
| Section | Experimental Uncertainties | |
| DOI | https://doi.org/10.1051/epjn/2018030 | |
| Published online | 14 November 2018 | |
https://doi.org/10.1051/epjn/2018030
Regular Article
From fission yield measurements to evaluation: status on statistical methodology for the covariance question
1
LPSC, Université Grenoble-Alpes, CNRS/IN2P3,
38026
Grenoble Cedex, France
2
CEA, DEN, DER, SPRC, LEPh, Cadarache Center,
13108
Saint Paul lez Durance, France
* e-mail: kessedjian@lpsc.in2p3.fr
Received:
5
December
2017
Received in final form:
21
March
2018
Accepted:
14
May
2018
Published online: 14 November 2018
Studies on fission yields have a major impact on the characterization and the understanding of the fission process and are mandatory for reactor applications. Fission yield evaluation represents the synthesis of experimental and theoretical knowledge to perform the best estimation of mass, isotopic and isomeric yields. Today, the output of fission yield evaluation is available as a function of isotopic yields. Without the explicitness of evaluation covariance data, mass yield uncertainties are greater than those of isotopic yields. This is in contradiction with experimental knowledge where the abundance of mass yield measurements is dominant. These last years, different covariance matrices have been suggested but the experimental part of those are neglected. The collaboration between the LPSC Grenoble and the CEA Cadarache starts a new program in the field of the evaluation of fission products in addition to the current experimental program at Institut Laue-Langevin. The goal is to define a new methodology of evaluation based on statistical tests to define the different experimental sets in agreement, giving different solutions for different analysis choices. This study deals with the thermal neutron induced fission of 235U. The mix of data is non-unique and this topic will be discussed using the Shannon entropy criterion in the framework of the statistical methodology proposed.
© B. Voirin et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Fission yields are important nuclear data for fuel cycle studies. The mass and isotopic yields of the fission fragments have a direct influence on the amount of neutron poisons that limit the fuel burnup but also on the residual power of the reactor after shutdown. Nowadays, fission yield evaluations are principally based on nuclear measurements dedicated to the fission process in the past and important information on systematic effects was not considered.
Fission yield evaluation comes from data and models to perform the best estimation of mass, isotopic and isomeric yields. Nowaday, the mass yields are deduced from the sum of the isotopic yields since it is the standard output of evaluation files. But without any correlation matrix, their uncertainties are greater for mass yields than for isotopic yields. This is in contradiction with experimental knowledge where the abundance of mass yield measurements is clearly dominant and often more accurate than isotopic yields. Thus, we expect the uncertainties on this latter observable to be lower than those on isotopic yields. Even if the isotopic yields are the interesting observables for the applications, the mass yield measurements provide an important constraint on the uncertainties of the isotopic yields. The inconsistency of mass yield uncertainties comes from the undefined covariance matrix in the current evaluations. Nevertheless, the covariance matrix depends on the evaluation process and its existence assumes that all measurements are statistically in agreement. These last years, different covariance matrices have been suggested but the experimental part of those are not taken into account [1–6].
Based on experimental knowledge on fission yield measurements, the goal of this study is to define a new methodology of evaluation based on statistical test to sort the different experimental measurements. The second section is devoted to introduce the tools needed in the discussion on the compatibility of the data. The third section deals with the data renormalization process and its consequence. The fourth section discusses our evaluation procedure according to the multiplicity of solutions. Absolute normalization step of mass yields with associated correlation matrix (Sect. 5) and the ranking of solutions (Sect. 6) are described in the end. And finally, conclusion and perspectives discuss the place of integral measurements in the evaluation framework.
2 Statistical test on the compatibility of available data
Fission yields are usually defined with a normalization over the light and heavy fragments equal to two due to the fact that binary fission corresponds to the major fission process in comparison to the ternary fission. The structure of the mass yields, with a very low yields for the symmetric masses (≈120 amu for major actinides), allows a normalization to the unit only for the light or the heavy fragments. In every case, the normalization induces a constraint. Then a multinomial distribution is expected for the description of these observables. As a consequence, negative correlation is expected if there is no systematic uncertainty. Nevertheless, the correlation matrices per measurement are not available in the database.
Through the EXFOR [7] database, we chose to test the methodology only on five important sets of measurements of the 235U(nth, f) reaction from Maeck et al. [8], Diiorio and Wehring [9], Thierens et al. [10], Bail [11] and Zeynalov et al. [12]. These data correspond to more than 215 measurements over 78 masses. With this selection, we cover at least all the heavy masses, allowing the normalization process. In this logic, at least we can assess the absolute normalization with the heavy mass peak which fixes light fragment yields. This is not the usual method used by the JEFF evaluation [13] which could highlight the normalization biases. Moreover, all these data sets are presented as already normalized by the authors. Thus, assuming independent Gaussian distributions without explicit information on correlation data, we can calculate the χ2 using the nA common measured mass number. This value is compared to the limited χ2 value ( ) given for a 99.5% confidence level. In practice, we calculate the P-value corresponding to the integral on [χ2 ; ∞ ] range of the χ2 distribution for (nA − 1) degrees of freedom. Table 1 presents the P-value for each bilateral statistical test. The Zeynalov dataset corresponds to pre-neutron mass yields. This allows us to evaluate the relevance of the statistical test procedure for inconsistent data identification related to the others ones which are post-neutron mass yields.
) given for a 99.5% confidence level. In practice, we calculate the P-value corresponding to the integral on [χ2 ; ∞ ] range of the χ2 distribution for (nA − 1) degrees of freedom. Table 1 presents the P-value for each bilateral statistical test. The Zeynalov dataset corresponds to pre-neutron mass yields. This allows us to evaluate the relevance of the statistical test procedure for inconsistent data identification related to the others ones which are post-neutron mass yields.
At the first step, we obtained a complete disagreement between all series. Therefore, we exclude the values of Maeck for the masses 135 and 136, since there is a clear mismatch between these values and the other ones (Fig. 1). We observe that only the data sets of Maeck and Diiorio in reference to Thierens one give a P-value greater than a quantile of 0.005 for a 99.5% confidence level (corresponding to the confidence level at 3 sigma for Gaussian distribution). Therefore, the validity of the normalization have to be tested for these selected data.
P-value for five sets of data. Results are presented according to a matrix since each set can be considered as a reference dataset. No bias appears when symmetrical P-value matrix is obtained. Only two sets are in agreement for a 99.5% confidence level (corresponding to a P-value greater than a quantile 1–0.995) if we consider Maeck set without the masses 135 and 136.
 |
Fig. 1 Cross-normalized data sets of fission yields for five main measurements for the 235U(nth, f) reaction. |
3 Renormalization of data sets
Many choices can be made to achieve the relative normalization between data sets. The simplest method is to define a reference mass A0 (e.g. A0 = 136). Then, we define a normalization factor to the reference set which introduces a systematic uncertainty for all the normalized data set. If we remind that measurement is the mean value of a random variable, the questioning about the normalization is multiple:
-
If we normalize directly via the random variables
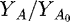 , the final distribution of mass A0,
, the final distribution of mass A0, 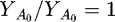 , corresponds to a Dirac distribution without variance. The distribution for masses other than the reference is the quotient of two Gaussian variables, which follows a Cauchy law. In all cases, we create a singularity on the reference mass from the others without making physical sense.
, corresponds to a Dirac distribution without variance. The distribution for masses other than the reference is the quotient of two Gaussian variables, which follows a Cauchy law. In all cases, we create a singularity on the reference mass from the others without making physical sense. -
The second solution proposed corresponds to a global normalization ki of all masses of ith set to the reference set. This solution provides simple covariance terms between masses of a same set (Fig. 2):
Cov (Ni (A) ; Ni (A′)) = var (ki) .
The masses used for the normalization represent the common masses between the two concerned data sets and change for each normalization. The cross-covariance terms between normalized sets are almost null due to the fact that ki and kj ∀ i, j ∈ [1, 4] are independent if all sets are initially independent (no initial covariance).
In the following, we use the second method considering the generalized χ2 based on covariance matrices of normalized sets. P -values between each set are presented in Table 2.
We observe that only three sets are in agreement for a 99.5% confidence level. In Figure 1, only the Zeynalov data present a clear shift to the heavy mass corresponding to a misclassification in EXFOR since these data are pre-neutron yield measurements. For the Bail set, a good agreement is presented in Figure 1 but the statistical test rejects this set. To go further and conclude on the reason of this disagreement, we have to consider the contribution of each mass to the statistical test.
 |
Fig. 2 Correlation of Maeck set after renormalization to Diiorio set as a function of mass measured. |
P-values for five sets of data after renormalization of data sets using the generalized χ2 method.
4 Tree of solutions
In the comparison of each set Ni(A) to the reference one Na(A), due to the relative normalization (Sect. 3), we have to consider the correlation matrix of Ni(A) in the generalized 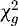 .
.
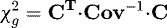 where C is the difference between two vectors of measurements and Cov−1 is the inverse covariance matrix associated to C:
where C is the difference between two vectors of measurements and Cov−1 is the inverse covariance matrix associated to C:
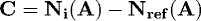 with covariance element :
with covariance element :
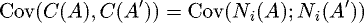 since Cov (Nref (A) ; Nref (A′)) = 0 (no experimental covariance is available).
since Cov (Nref (A) ; Nref (A′)) = 0 (no experimental covariance is available).
Therefore, the generalized 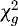 can be seen as the scalar product of the vector Z on the transposed vector CT:
can be seen as the scalar product of the vector Z on the transposed vector CT:
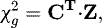
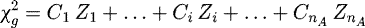 with
with
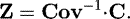
The ith contribution to 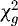 (scalar), noted
(scalar), noted 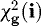 (vector), corresponds to the ith term of the sum:
(vector), corresponds to the ith term of the sum:
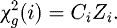
For the Zeynalov data set, the test gives a negative output due to the misclassification. We naturally exclude all these points to build the mean values of the mass yield measurements and the associated uncertainties. For the Bail data set, the global 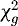 value is principally given by the contribution of the mass 128 which is in disagreement with the other ones (Fig. 3). On this plot, we compare the simple χ2 calculations and the generalized
value is principally given by the contribution of the mass 128 which is in disagreement with the other ones (Fig. 3). On this plot, we compare the simple χ2 calculations and the generalized 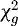 calculations. It is clear that the second one (
calculations. It is clear that the second one (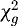 ) is expressly needed for a relevant test of compatibility.
) is expressly needed for a relevant test of compatibility.
We also note that the relative normalization to another set changes according to the common masses selected. Then, the selection of the data using renormalization and statistical test must have a feedback to the renormalization process to limit the biases on the final mean values of yields and their uncertainties. In the end, we selected the data sets of Maeck, Diiorio, Thierens and Bail (except mass 128). At this step, for instance, we can conclude for the mass 128 there are two incompatible solutions: the first one is the mean value of Maeck, Diiorio and Thierens and the second one is the Bail value. It is the same for the mass 135 and 136 from Maeck which are incompatible with those of others sets.
The 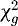 test allows us to make a choice on the compatibility of data with a given confidence level. Thus, for each incompatibility, a branch of the tree of solutions is open to get all the possibilities provided by the experiments. The classical solution of the blind mean value considering, or not, penalties in case of disagreement is a non-choice which washes the information given by the experiments. In this method, the choice is based on a regular statistical method to reach the best values with limited bias and provide realistic variance–covariance matrix.
test allows us to make a choice on the compatibility of data with a given confidence level. Thus, for each incompatibility, a branch of the tree of solutions is open to get all the possibilities provided by the experiments. The classical solution of the blind mean value considering, or not, penalties in case of disagreement is a non-choice which washes the information given by the experiments. In this method, the choice is based on a regular statistical method to reach the best values with limited bias and provide realistic variance–covariance matrix.
 |
Fig. 3 Contribution to the χ2 and |
5 Absolute normalization of mass yields
After the selection of compatible mass yield data, the goal is to deduce the mean values of renormalized measurements and the variance–covariance matrix taking into account the covariance matrix of renormalized data (Fig. 2). The self-normalization of fission yields allows the determination of absolute yields if all the mass range is covered (statistically, very low yields do not change significantly the absolute normalization). Nevertheless, at this moment, an arbitrary choice is done to select the reference set needed for the renormalization. Therefore, new calculations have been achieved changing the reference set. For the four selected data sets, the self-normalization of mean mass yields provides a constraint on the results. We observe a good agreement between all mean values for the four evaluations as a function of mass (Fig. 4). Figure 5 presents the standard deviations of evaluated mass yields as a function of mass for the four different reference sets. Correlations of each evaluation is shown in Figure 6 and present many important differences in the structures. The uncertainty propagation method dedicated to fission yields corresponds to the perturbation theory and is described in references [14,15]. This is clearly due to the correlation matrix deduced from the renormalized data. Indeed, the systematic uncertainties from ki=1,4 normalization factors depend in part of the uncertainties of the reference data set. Choice has to be done to disentangle the four different solutions given by a single compatible dataset.
 |
Fig. 4 Evaluations of 235U(nth, f) mass yields based on reference data sets. A very good agreement between evaluations and the JEFF3.1 library is observed. |
 |
Fig. 5 Relative uncertainties of the different evaluations are displayed as a function of mass. Important discrepancies appear according to the choice of the reference yield data set. |
 |
Fig. 6 For each evaluation, the correlation matrix is represented as a function of mass. Results present some large discrepancies as a function of the reference data set used for the cross-normalization of data sets. |
6 Ranking of analysis paths
From our analysis, since we can change the reference data set, four solutions are obtained with very different uncertainties and correlation matrices. To interpret the correlation matrix, eigenvalues (EVi=1,n) are computed to compare quantities of information provided by the solutions [16]. The matrix traces are always equal to the number of evaluated masses (78 in this study) but the cumulative curve of eigenvalues are drastically different for the four solutions of the analysis (Fig. 7 (up)). We observe that only the data sets of Maeck and Diiorio in reference to Thierens one give a P -values greater than a quantile of 0.005 for a 99.5% confidence level). These curves represent the spectra of the correlation matrices. Two additional "school cases" are presented: i) a diagonal correlation corresponding to null covariance terms; ii) an exponential eigenvalue spectrum. The Shannon entropy SSh is chosen as a useful criterion to assess the brewing of information [17]. It is given by the relation:
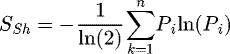 where n is the number of eigenvalues. We approximate the probability with the weight of each component of the eigenvalue decomposition to built a relative criterion. The weight of the information is provided according to the equation:
where n is the number of eigenvalues. We approximate the probability with the weight of each component of the eigenvalue decomposition to built a relative criterion. The weight of the information is provided according to the equation:
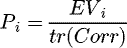 with tr(Corr) = 78 is the correlation matrix trace (in this study, 78 evaluated mass yields). Indeed, a large eigenvalue reflects an important component of the information carried by the assessed data, a low eigenvalue corresponds to a non-significant information due to the important correlations between mass yields. Figure 7 (down) presents the Shannon entropy calculation for a diagonal correlation matrix (null covariance term Cov = 0), an exponential spectrum of eigenvalues and the spectra of the four solutions analyzed. We note that the maximum of entropy appears for null covariance terms. In general case, the minimal entropy is given for a full correlated dataset. In our example, the minimum of entropy corresponds to the exponential spectrum of eigenvalues. The entropie values of the mass yields analyzed are distributed between these two extrema. We interpreted the results as following to select the possible choices of evaluations:
with tr(Corr) = 78 is the correlation matrix trace (in this study, 78 evaluated mass yields). Indeed, a large eigenvalue reflects an important component of the information carried by the assessed data, a low eigenvalue corresponds to a non-significant information due to the important correlations between mass yields. Figure 7 (down) presents the Shannon entropy calculation for a diagonal correlation matrix (null covariance term Cov = 0), an exponential spectrum of eigenvalues and the spectra of the four solutions analyzed. We note that the maximum of entropy appears for null covariance terms. In general case, the minimal entropy is given for a full correlated dataset. In our example, the minimum of entropy corresponds to the exponential spectrum of eigenvalues. The entropie values of the mass yields analyzed are distributed between these two extrema. We interpreted the results as following to select the possible choices of evaluations:
-
a maximum of entropy translates the best brewing of information. This analysis corresponds to the evaluation with a normalization based on Diiorio dataset;
-
a minimum of entropy corresponds to the larger constraint on the results.
These two extrema could be interesting to provide the best compromise of all the data for a lower cost of uncertainties or to provide the hardest test of models according to the experimental data. Figure 8 shows the mass yield evaluation with a maximum of entropy for the 235U(nth, f) reaction in comparison to the JEFF-3.1.1 [13] and the ENDF/B-VII.1 libraries [18]. A very good agreement is obtained with both libraries for this pure experimental mass yield evaluation. The uncertainties of these results correspond to the red dots in Figure 5. Shannon's entropy analysis helps us to discriminate the different evaluations that are similar for mean values but not for covariance. The correlation matrix (based on Diiorio renormalization) is plotted as a function of the mass range (Fig. 6b). We observe clear structures, with positive components corresponding to the cross-normalization of data sets and negative components from the constraint of the self-normalization of the fission yields (Sect. 5).Experimental data consideration is crucial for the definition of the evaluation covariance in complement to covariance from the models. A large range of data is listed in the EXFOR data bank. Moreover, a lot of them covers partial mass ranges which supposed a cross-normalization of data, for different incident neutron energies and not necessarily with an absolute mass (or nuclear charge) identification. The mix of all data could be non-unique and this topic has been discussed in the framework of the statistical methodology proposed. This work deals with a general methodology to assess the fission yields and their covariance matrix. This study on the 235U(nth, f) reaction is based on statistical generalized 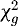 tests to build a consistent data set through the existing measurements present in the EXFOR database. The analysis provides several solutions, considering the covariance due to the analysis paths. Then, a hierarchy of solutions is built according to the Shannon entropy. For this reaction, a pure experimental mass yield assessment with consistent variance-covariance is provided due to the numerous existing data.
tests to build a consistent data set through the existing measurements present in the EXFOR database. The analysis provides several solutions, considering the covariance due to the analysis paths. Then, a hierarchy of solutions is built according to the Shannon entropy. For this reaction, a pure experimental mass yield assessment with consistent variance-covariance is provided due to the numerous existing data.
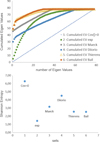 |
Fig. 7 (Up) for each correlation matrix of evaluations, cumulated eigenvalues (EV) are plotted as a function of the number of EV. For instance, we represent also the cumulated EV for null covariance terms and for an exponential distribution of EV. (Down) Shannon entropies as a function of the data set number with respect to the index in the previous legend. |
 |
Fig. 8 Chosen evaluation of 235U(nth, f) mass yields according to the maximum Shannon entropy in comparison to the JEFF-3.1 and the ENDF/B-VII.1 libraries. A very good agreement is observed all over the mass range for both libraries. |
7 Conclusion and perspectives
Experimental data consideration is crucial for the definition of the evaluation covariance in complement to covariance from the models. A large range of data is listed in the EXFOR data bank. Moreover, a lot of them covers partial mass ranges which supposed a cross-normalization of data, for different incident neutron energies and not necessarily with an absolute mass (or nuclear charge) identification. The mix of all data could be non-unique and this topic has been discussed in the framework of the statistical methodology proposed. This work deals with a general methodology to assess the fission yields and their covariance matrix. This study on the 235U (nth, f) reaction is based on statistical generalized 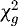 tests to build a consistent data set through the existing measurements present in the EXFOR database. The analysis provides several solutions, considering the covariance due to the analysis paths. Then, a hierarchy of solutions is built according to the Shannon entropy. For this reaction, a pure experimental mass yield assessment with consistent variance-covariance is provided due to the numerous existing data.
tests to build a consistent data set through the existing measurements present in the EXFOR database. The analysis provides several solutions, considering the covariance due to the analysis paths. Then, a hierarchy of solutions is built according to the Shannon entropy. For this reaction, a pure experimental mass yield assessment with consistent variance-covariance is provided due to the numerous existing data.
A scheme of the procedure is shown Figure 9: same datasets provide different solutions for the mass range (e.g. mass 128) which are true a priori. Several solutions are funded for the covariance matrix corresponding to identical mean values of mass yields. A ranking of solutions is proposed using the Shannon entropy to select an evaluation. Future work will proposed to compare this evaluation to fission models (GEF, FIFRELIN, etc.) or cumulative data to test the consistency of these evaluated data.
Unfortunately, the measurements of isotopic and isomeric distributions do not cover the range of isotopes requested for the applications. The use of models is unavoidable. Using the present results on mass yield evaluation and its covariance matrix, the goal is to validate the phenomenological fission models using a Bayesian comparison to perform a physical pre-selection of possible evaluations. Thus, for each solution, the goal is to provide a complete evaluation with its variance-covariance matrix. This second step is illustrated in Figure 6b. At the end, the benchmark on integral measurements and the cumulative yields built on the isotopic yields will allow us to refine the hierarchy of the possible solutions of the parent fission yields.
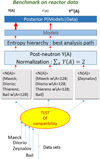 |
Fig. 9 Scheme of the analysis path: statistical test is needed to identify the compatible measurements per set and not only per mass. For all series, covariance matrices are defined in order to take into account the different analysis paths. Final results represent all the solutions given by the microscopic data which will be compared to integral measurements or cumulative mass yields. |
Author contribution Statement
This work corresponds to the Ph.D. work of B. Voirin and G. Kessedjian, A. Chebboubi and O. Serot are Ph.D. supervisors. All coauthors have been involved in the definition of the statistical analysis critera and the redaction of this article.
Acknowledgments
This work was supported by IN2P3, the University of Grenoble Alpes, Grenoble-INP and le défi NEEDS.
References
- L. Fiorito et al., Ann. Nucl. Energy 69, 331 (2014) [CrossRef] [Google Scholar]
- A. Chebboubi et al., EPJ Web Conf. 146, 04021 (2017) [CrossRef] [Google Scholar]
- K.H. Schmidt et al., Nucl. Data Sheets 131, 107 (2016) [CrossRef] [Google Scholar]
- N. Terranova et al., Nucl. Data Sheets 95, 225230 (2015) [Google Scholar]
- D. Rochman et al., Ann. Nucl. Energy 131, 125 (2016) [CrossRef] [Google Scholar]
- O. Leray et al., EPJ Web Conf. 146, 09023 (2017) [CrossRef] [Google Scholar]
- EXFOR database, https://www-nds.iaea.org/exfor/exfor.htm [Google Scholar]
- W.J. Maeck et al., Allied Chem. Corp., Idaho Chem. Programs 1142, 09 (1978) [Google Scholar]
- G. Diiorio, B.W. Wehring, Nucl. Instrum. Methods 147, 487 (1977) [CrossRef] [Google Scholar]
- H. Thierens et al., Nucl. Instrum. Methods 134, 299 (1976) [Google Scholar]
- A. Bail, Ph.D. thesis, Université Sciences et Technologies − Bordeaux I, 2009 [Google Scholar]
- S. Zeynalov et al., in 13th International Seminar on Interaction of Neutrons with Nuclei ISINN-13, Dubna, 2005 [Google Scholar]
- M.A. Kellet et al., JEFF-3.1/3.1.1, JEFF Report 20, 2009, ISBN 978-92-64-99087-6 [Google Scholar]
- F. Martin, Ph.D. thesis, Université de Grenoble, 2013 [Google Scholar]
- G. Kessedjian, HDR, Université de Grenoble, 2015 [Google Scholar]
- G. Kessedjian et al., Phys. Rev. C 85, 044613 (2012) [CrossRef] [Google Scholar]
- B. Diu, C. Guthmann, B. Roulet, D. Lederer, Physique statistique (Hermann, 1996) [Google Scholar]
- M.B. Chadwick et al., Nucl. Data Sheets 112, 2887 (2011) [CrossRef] [Google Scholar]
Cite this article as: Brieuc Voirin, Grégoire Kessedjian, Abdelaziz Chebboubi, Sylvain Julien-Laferrière, Olivier Serot, From fission yield measurements to evaluation: status on statistical methodology for the covariance question, EPJ Nuclear Sci. Technol. 4, 26 (2018)
All Tables
P-value for five sets of data. Results are presented according to a matrix since each set can be considered as a reference dataset. No bias appears when symmetrical P-value matrix is obtained. Only two sets are in agreement for a 99.5% confidence level (corresponding to a P-value greater than a quantile 1–0.995) if we consider Maeck set without the masses 135 and 136.
P-values for five sets of data after renormalization of data sets using the generalized χ2 method.
All Figures
 |
Fig. 1 Cross-normalized data sets of fission yields for five main measurements for the 235U(nth, f) reaction. |
| In the text | |
 |
Fig. 2 Correlation of Maeck set after renormalization to Diiorio set as a function of mass measured. |
| In the text | |
 |
Fig. 3 Contribution to the χ2 and |
| In the text | |
 |
Fig. 4 Evaluations of 235U(nth, f) mass yields based on reference data sets. A very good agreement between evaluations and the JEFF3.1 library is observed. |
| In the text | |
 |
Fig. 5 Relative uncertainties of the different evaluations are displayed as a function of mass. Important discrepancies appear according to the choice of the reference yield data set. |
| In the text | |
 |
Fig. 6 For each evaluation, the correlation matrix is represented as a function of mass. Results present some large discrepancies as a function of the reference data set used for the cross-normalization of data sets. |
| In the text | |
 |
Fig. 7 (Up) for each correlation matrix of evaluations, cumulated eigenvalues (EV) are plotted as a function of the number of EV. For instance, we represent also the cumulated EV for null covariance terms and for an exponential distribution of EV. (Down) Shannon entropies as a function of the data set number with respect to the index in the previous legend. |
| In the text | |
 |
Fig. 8 Chosen evaluation of 235U(nth, f) mass yields according to the maximum Shannon entropy in comparison to the JEFF-3.1 and the ENDF/B-VII.1 libraries. A very good agreement is observed all over the mass range for both libraries. |
| In the text | |
 |
Fig. 9 Scheme of the analysis path: statistical test is needed to identify the compatible measurements per set and not only per mass. For all series, covariance matrices are defined in order to take into account the different analysis paths. Final results represent all the solutions given by the microscopic data which will be compared to integral measurements or cumulative mass yields. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.