| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
|
|
|---|---|---|
| Article Number | 28 | |
| Number of page(s) | 5 | |
| Section | Nuclear Models | |
| DOI | https://doi.org/10.1051/epjn/2018043 | |
| Published online | 14 November 2018 | |
https://doi.org/10.1051/epjn/2018043
Regular Article
Influence of nuclear structure data on fission observables
1
CEA, DEN, Cadarache,
13108
Saint-Paul-lez-Durance, France
2
IRFU, CEA, Université Paris-Saclay,
91191
Gif-sur-Yvette, France
* e-mail: olivier.litaize@cea.fr
Received:
5
December
2017
Received in final form:
18
May
2018
Accepted:
8
June
2018
Published online: 14 November 2018
The simulation of the de-excitation of nuclei requires some models and data in order to construct the nuclear level scheme and the associated transition intensities. The aim of this work is to focus on nuclear structure data used at low energy where electromagnetic transitions can be measured. The RIPL3 database linked to the FIFRELIN Monte Carlo code contains such data and their influence on fission observables is reviewed.
© O. Litaize et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The aim of this work is to illustrate the influence of nuclear structure data on fission observables. To do that we consider a Monte Carlo simulation of the de-excitation of fission fragments by neutron/gamma/conversion electron emission. FIFRELIN [1,2] is a Monte Carlo code developed at CEA which offers this capability by relying on nuclear structure data at low excitations energies (level schemes and transition intensities for instance). Section 2 is a short description of the de-excitation process performed in the FIFRELIN code while Section 3 resumes the type of nuclear structure data used in the code. Section 4.1 highlights the role of the half-life of levels when comparing prompt gamma spectra measured in coincidence with fission fragments. The influence of a modification of the neutron separation energy is illustrated in Section 4.2. Section 4.3 deals with the influence of the delayed neutron emission probability and Section 4.4 shows the importance of an accurate knowledge of the level scheme.
2 Fission fragment de-excitation
The simulation of the de-excitation of fission fragments starts by the sampling of the mass A, the nuclear charge Z, the kinetic energy KE, the excitation energy E, the spin J and the parity π of an initial state. The three first characteristics are usually based on pre-neutron emission experimental data while the three last characteristics require some assumptions and models because of the scarce information available for excitation and spin-parity sharing between fragments right after scission. In FIFRELIN fission fragments excitation energy and spin are estimated by using a mass-dependent temperature ratio law RT(A) (involving two free parameters) and a spin cut-off parameter (involving one to two additional free parameters depending on the spin cut-off model). Another free parameter is used for the fragment moment of inertia which is set as a fraction of a spheroid rigid body. Once the initial states of a fragment pair (binary fission) are known, the de-excitation occurs. The de-excitation through neutron, gamma and conversion electrons is performed by using the notion of Nuclear Realization (NR) first established by Becvar [3] for radiative capture reactions and extended by Regnier et al. [4] to neutron/gamma/electron coupled emission from an excited nucleus (here a fission fragment). A nuclear realization of the level scheme of a nucleus consists in the knowledge of the complete level scheme and the partial widths allowing the decay of a level to another one. Porter-Thomas fluctuations of partial widths are naturally accounted for in such a process as described in [4]. Such a scheme allows the estimation of a statistical uncertainty as well as an uncertainty due to the bad knowledge of nuclear structure. Indeed, the estimation of an average quantity fluctuates from a NR to another NR simply due to the statistical nature of a NR. Finally, the five free parameters discussed above are used to reproduce a fission target (e.g. the average total prompt neutron multiplicity 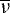 ).
).
3 Nuclear structure data
Different nuclear structure data are used for the simulation of the de-excitation of fission fragments. In FIFRELIN these data are provided by the RIPL3 database [5]. A new release has been delivered in August 2015 [6]. In addition, the knowledge of nuclear masses, provided by AME2012 [7,8], is required e.g. for the calculation of the fission fragment kinetic energy after neutron emission. These data are consistent with the neutron separation energy provided in RIPL3-2015. Differences between this release and the previous one have an impact on the estimation of fission observables. The main data accounted for in FIFRELIN are summarized hereafter:
-
neutron separation energy Sn;
-
number of levels;
-
energy of the last level below which the scheme is supposed to be complete (at least the energy of the levels inside the scheme are known but their spin and parity can be unassigned);
-
energy of the levels;
-
spin and parity of the levels (they are sampled if not given);
-
number of transitions;
-
decay branching ratio;
-
half-life T½;
-
gamma intensities
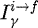 ;
; -
Internal Conversion Coefficient ICC.
These data allow the simulation of the low energy part of the cascade by emission of gamma-rays and conversion electrons (number and energy of gamma and conversion electrons). In addition if a level has a β−n emission probability an estimation of the average number of delayed neutrons can be performed (in fact the cumulative yields must be calculated as it will be explained in Sect. 4.3).
For instance in RIPL3-2015, the 88Br neutron separation energy Sn is roughly equal to 4.896 MeV. There are 9 known levels and 14 transitions. Only the ground state is fully known (energy E, spin J, parity π, half-life T½) and the 8 additional levels have unassigned spin/parity. In that case FIFRELIN samples Jπ from theoretical laws. By default positive and negative parities are supposed to be equally likely and spin is sampled, following the work of Bethe [9,10], from a distribution accounting for a spin cut-off parameter. At high energy this parameter follows a Fermi gas model and at low energy where the level density is in agreement with the discrete level scheme, a discrete spin cut-off parameter is used as proposed in [11].
4 Influence of nuclear structure data on fission observables
The prompt fission gamma spectrum (PFGS) calculated by FIFRELIN in the case of the spontaneous fission of 252Cf is in good agreement with experimental values [12] but even if the shape is well reproduced, the average multiplicity is higher by roughly 10%. As shown in Figure 1 roughly half of the calculated low-energy gamma spectrum is purely calculated from level density and photon strength function models while the other half comes from gamma intensities provided in the database. Several explanations for this overestimation can be presented:
-
bad or missing spin assignment;
-
missing half-lives (some states could be nano-second isomers or micro-second isomers);
-
incorrect gamma-ray intensities;
-
incorrect conversion coefficients;
-
bad level densities;
-
bad photon strength functions.
 |
Fig. 1 FIFRELIN calculation of the prompt fission gamma spectrum of 252Cf(sf) reaction. Total spectrum, simulated part from level densities and photon strength functions and simulated part from gamma-ray intensities provided by database are shown as black, blue and red histograms respectively. |
4.1 Influence of the half-life
The influence of the half-life is exemplified in Figure 2 between 50 and 300 keV and in Figure 3 between 500 and 700 keV. Almost all the transitions are of the order of few nanoseconds between 125 and 280 keV while between 550 keV and 700 keV longer half-lives seem to be responsible of the spectral curve (1 μs transitions are far from 5 ns transitions). In correlation with the gamma energy of these transitions, these longer half-life transitions (more than few nanoseconds) seem to be emitted by nuclei in the mass range A = [130, 145] and in a lesser extend A = [90, 105] (Fig. 4).
 |
Fig. 2 Influence of the half-life of levels on the prompt fission gamma spectrum between 50 and 300 keV. |
 |
Fig. 3 Influence of the half-life of levels on the prompt fission gamma spectrum between 500 and 700 keV. |
 |
Fig. 4 Influence of the half-life of levels on the average prompt fission gamma multiplicity as function of pre-neutron fragment mass. |
4.2 Influence of the neutron separation energy Sn
Table 1 provides different nuclei for which the neutron separation energy has changed since the last release of the RIPL3 database. The influence of a modification of Sn is exemplified on the thermal neutron induced binary fission of 235U leading to the 102Y + 134I fragment pair. In the case of 102Y, the Sn value is lowered by almost 900 keV in the present release of RIPL3-2015. This leads to an increase of about 10% of the average neutron multiplicity as well as the gamma multiplicity. In the same time, the conversion electron multiplicity of the fragment pair is increased by 60%. Nevertheless the example of 102Y is an extreme case: almost all levels of this odd-odd neutron rich nucleus have unknown spin-parities. Not only Sn has changed and for instance a level (T½ = 360 ms) having an uncertain energy assignment in RIPL3-2009 was set to 200 keV in RIPL3-2015 (Tab. 2).
Sn differences from RIPL3-2009 to RIPL3-2015.
Influence of Sn on average multiplicities.
4.3 Influence of the delayed neutron emission probability Pn
There were no Pn values for 88Br, 96Rb, 86As in RIPL3-2009 release leading to a strong underestimation of the delayed neutron fraction. It is now corrected in the new release since 2015. In FIFRELIN we can calculate without additional cost the number of delayed neutron that will be emitted at the end of the prompt de-excitation cascade. This is allowed by the fact that the database provides the β−n probabilities. Note that this is not exactly the true delayed neutron fraction 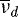 but a related parameter that we will write
but a related parameter that we will write 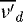 because it takes into account the independent fission fragment yields calculated during the prompt cascade and not the cumulative yields. This parameter can not be compared to experimental values but the influence of the Pn values can be highlighted here in the case of 235U(nth,f) and 237Np(n,f) reactions where an increase of 15% can be observed (see Tab. 3).
because it takes into account the independent fission fragment yields calculated during the prompt cascade and not the cumulative yields. This parameter can not be compared to experimental values but the influence of the Pn values can be highlighted here in the case of 235U(nth,f) and 237Np(n,f) reactions where an increase of 15% can be observed (see Tab. 3).
Delayed neutron fraction for thermal fission of 235U and 800 keV neutron induced fission of 237Np.
The uncertainty of ∼15 × 10−5 quoted in Table 3 is statistical. For this observable (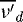 ), the present simulation leads to a 3 times higher uncertainty due to fluctuating NRs (∼40 × 10−5).
), the present simulation leads to a 3 times higher uncertainty due to fluctuating NRs (∼40 × 10−5).
4.4 Influence of the nuclear level scheme
The last example highlights the need for an update of nuclear level schemes. As previously mentioned the low energy part of the scheme is provided by nuclear structure experiments while it is completed at higher energy by level density models. A good level density leads to a good feeding of low energy levels and constitutes a constraint of the models. Among other, 92Kr has a modified level scheme in RIPL3-2015 compared to the previous release. This kind of update is crucial for comparing fission gamma spectra but could be undetectable in a global fission spectrum without fission fragment selection. Such a selection can be performed through the analysis of triple coincidences (γ − γ − γ cubes) [13]. Experimental data come from the EXILL campaign [14] involving a large array of sixteen HPGe detectors placed at the end of the PF1B cold neutron guide at the Institut Laue Langevin (ILL) in Grenoble. It included eight EXOGAM clovers, two smaller clovers from LOHENGRIN and six large efficiency detectors from GASP. We have focused the analysis on 92Kr because in the 235U(nth,f) reaction, its complementary partner after neutron emission is 142Ba. This latest nucleus has a high production yield and its level scheme is complete up to 1.848 MeV with 38 levels known up to 5.284 MeV. When two strong transitions are selected (one per complementary partner), the rest of the cascade in 92Kr can be reconstructed. Nuclear level scheme and gamma transitions of 92Kr are shown for the 235U(nth,f) reaction in Figures 5–7. The cut-off energy provided by RIPL3-2015 for 92Kr is 2.35 MeV corresponding to the 14th level. 29 additional levels are partially known (at least the position in energy is known but the spin/parity is sometimes missing and must be completed). Figure 5 corresponds to the experimental data analyzed and already reported in [13]. Figure 6 shows the calculated gamma cascade associated to the reconstructed level scheme (coming from RIPL3-2009 for the most part at low energy). With this release of the database, the intensities of the two 4+ → 2+ transitions at 1297.1 and 1034.9 keV are reversed compared to EXILL data. By using RIPL3-2015 database and completing the level scheme with FIFRELIN (Fig. 7) the situation, while not perfect, is a step forward. Remember that the goal of the calculation is to reproduce the average prompt neutron multiplicity 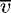 and to predict over fission observables. In this way the calculation scheme is not tuned to reproduce the specific cascade of 92Kr. Reproducing the cascade (in addition of
and to predict over fission observables. In this way the calculation scheme is not tuned to reproduce the specific cascade of 92Kr. Reproducing the cascade (in addition of 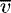 ) is simply an additional constraint for the model. If the lower part of the level scheme is known with better accuracy (in the new release of the database) then the model parameters that drive the initial fission fragment spin can be better inferred. Practically in this work it is clear that the overfeeding of high spin states in the current calculation scheme of FIFRELIN (initial spin cut-off models) leads to high intensities in transitions at 688 keV and 849.3 keV. This was already observed for other nuclei by using the previous release of the database as reported in [15] related to isomeric yields.
) is simply an additional constraint for the model. If the lower part of the level scheme is known with better accuracy (in the new release of the database) then the model parameters that drive the initial fission fragment spin can be better inferred. Practically in this work it is clear that the overfeeding of high spin states in the current calculation scheme of FIFRELIN (initial spin cut-off models) leads to high intensities in transitions at 688 keV and 849.3 keV. This was already observed for other nuclei by using the previous release of the database as reported in [15] related to isomeric yields.
 |
Fig. 5 Partial level scheme and gamma-cascade of 92Kr analyzed from EXILL experiment measured in coincidence with 142Ba. |
 |
Fig. 6 Low energy part of the level scheme and gamma-cascade of 92Kr calculated with FIFRELIN (RIPL3-2009). The intensities of 1034 and 1297 keV transitions are reversed. |
 |
Fig. 7 Low energy part of the level scheme and gamma-cascade of 92Kr calculated with FIFRELIN (RIPL3-2015). The intensities of 1034 and 1297 keV transitions are respected. |
5 Conclusion
We have shown the influence of nuclear structure data on several fission observables. The simulation of the de-excitation of fission fragments is strongly dependent on these data specially at low energies, roughly below 1 MeV, within the discrete energy level region. The impact can be seen on global observables such as average gamma multiplicities and spectra but also on delayed neutron multiplicity due to lack of knowledge in neutron emission probabilities or missing β, γ intensities. The latter topic can be investigated through total absorption γ-ray spectroscopy performed with large 4π scintillation detectors as it has been done recently for some fission products [16].
Author contribution statement
All the authors are involved in the FIFRELIN project (development of the code or studies with the code).
References
- O. Litaize, O. Serot, Phys. Rev. C 82, 054616 (2010) [Google Scholar]
- O. Litaize, O. Serot, L. Berge, Eur. Phys. J. A 51, 177 (2015) [Google Scholar]
- F. Becvar, Nucl. Instrum. Methods Phys. Res. Sect. A 417, 434 (1998) [Google Scholar]
- D. Regnier, O. Litaize, O. Serot, Comput. Phys. Commun. 201, 19 (2016) [Google Scholar]
- R. Capote, M. Herman, P. Oblozinsky, P. Young, S. Goriely, T. Belgya, A. Ignatyuk, A. Koning, S. Hilaire, V. Plujko, M. Avrigeanu, O. Bersillon, M. Chadwick, T. Fukahori, Z. Ge, Y. Han, S. Kailas, J. Kopecky, V. Maslov, G. Reffo, M. Sin, E. Soukhovitskii, P. Talou, Nucl. Data Sheets 110, 3107 (2009) [NASA ADS] [CrossRef] [Google Scholar]
- M. Verpelli, R. Capote, in International Nuclear Data Committee, INDC(NDS)-0702 (2015) [Google Scholar]
- G. Audi, M. Wang, A. Wapstra, F. Kondev, M. MacCormick, X. Xu, B. Pfeiffer, Chin. Phys. C 36, 1287 (2012) [Google Scholar]
- M. Wang, G. Audi, A. Wapstra, F. Kondev, M. MacCormick, X. Xu, B. Pfeiffer, Chin. Phys. C 36, 1603 (2012) [Google Scholar]
- H.A. Bethe, Phys. Rev. 50, 332 (1936) [CrossRef] [Google Scholar]
- H.A. Bethe, Rev. Mod. Phys. 9, 69 (1937) [Google Scholar]
- A. Koning, S. Hilaire, S. Goriely, Nucl. Phys. A 810, 13 (2008) [CrossRef] [Google Scholar]
- A. Oberstedt, R. Billnert, F-J. Hambsch, S. Oberstedt, Phys. Rev. C 92, 014618 (2015) [CrossRef] [Google Scholar]
- T. Materna, M. Rapala, A. Letourneau, A. Marchix, O. Litaize, O. Serot, W. Urban, A. Blanc, M. Jentschel, U. Köster, P. Mutti, T. Soldner, G. Simpson, C.A. Ur, G. De France, EPJ Web Conf. 146, 04041 (2017) [CrossRef] [Google Scholar]
- M. Jentschel et al., J. Instrum. 12, P11003 (2017) [Google Scholar]
- A. Etilé, O. Roig, E. Bauge, L. Gaudefroy, V. Méot, EPJ Web Conf. 146, 09027 (2017) [CrossRef] [Google Scholar]
- E. Valencia et al., Phys. Rev. C 95, 024320 (2017) [Google Scholar]
Cite this article as: Olivier Litaize, Abdelaziz Chebboubi, Olivier Serot, Loïc Thulliez, Thomas Materna, Michal Rapala, Influence of nuclear structure data on fission observables, EPJ Nuclear Sci. Technol. 4, 28 (2018)
All Tables
Delayed neutron fraction for thermal fission of 235U and 800 keV neutron induced fission of 237Np.
All Figures
 |
Fig. 1 FIFRELIN calculation of the prompt fission gamma spectrum of 252Cf(sf) reaction. Total spectrum, simulated part from level densities and photon strength functions and simulated part from gamma-ray intensities provided by database are shown as black, blue and red histograms respectively. |
| In the text | |
 |
Fig. 2 Influence of the half-life of levels on the prompt fission gamma spectrum between 50 and 300 keV. |
| In the text | |
 |
Fig. 3 Influence of the half-life of levels on the prompt fission gamma spectrum between 500 and 700 keV. |
| In the text | |
 |
Fig. 4 Influence of the half-life of levels on the average prompt fission gamma multiplicity as function of pre-neutron fragment mass. |
| In the text | |
 |
Fig. 5 Partial level scheme and gamma-cascade of 92Kr analyzed from EXILL experiment measured in coincidence with 142Ba. |
| In the text | |
 |
Fig. 6 Low energy part of the level scheme and gamma-cascade of 92Kr calculated with FIFRELIN (RIPL3-2009). The intensities of 1034 and 1297 keV transitions are reversed. |
| In the text | |
 |
Fig. 7 Low energy part of the level scheme and gamma-cascade of 92Kr calculated with FIFRELIN (RIPL3-2015). The intensities of 1034 and 1297 keV transitions are respected. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


