| Issue |
EPJ Nuclear Sci. Technol.
Volume 2, 2016
|
|
|---|---|---|
| Article Number | 20 | |
| Number of page(s) | 5 | |
| DOI | https://doi.org/10.1051/epjn/2016015 | |
| Published online | 15 April 2016 | |
https://doi.org/10.1051/epjn/2016015
Regular Article
Lock-in thermography for characterization of nuclear materials
Den-Service d’Études Analytiques et de Réactivité des Surfaces (SEARS), CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
⁎ e-mail: alexandre.semerok@cea.fr
Received:
23
September
2015
Received in final form:
2
February
2016
Accepted:
22
February
2016
Published online:
15
April
2016
A simplified procedure of lock-in thermography was developed and applied for characterization of nuclear materials. The possibility of thickness and thermal diffusivity measurements with the accuracy better than 90% was demonstrated with different metals and Zircaloy-4 claddings.
© A. Semerok et al., published by EDP Sciences, 2016
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Lock-in thermography is a non-destructive method which may be applied to test and to ensure remote control over materials in severe environment (e.g. nuclear installations) in a wide temperature range. The method is based on the laser heating of a sample with a modulated laser power at a given frequency f(Hz) followed by measurements of a thermal radiation emitted by the sample. The phase shifts Δϕ between the laser power and the thermal radiation measured at different modulated frequencies are then compared with those obtained with an analytical (3D + t) model developed at the LISL (DEN/DANS/DPC/SEARS) in case of the heating of a sample covered by a deposited layer [1,2]. Thus, it is possible to provide a tool to characterize some sample properties (thickness, thermal diffusivity, deposited layer/surface thermal contact resistance, characterization of under-surface defects and their evolution with time). The phase shift of heating temperature is presented in Figure 1.
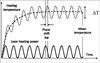 |
Fig. 1 Phase shift of heating temperature. |
2 Model for the heating of a plate
In a thermal model for homogeneous and isotropic plate with infinite dimensions, we supposed that:
-
variations of the optical and thermal properties for a surface covered by a deposited layer during its heating are negligible;
-
the surface roughness effect and heat exchange due to the sample surface/air convection are also negligible.
In the heating models [1,2] for a surface with a deposited layer, we supposed that the layer/surface thermal resistance (ℜ) and the layer optical thickness (αL) on laser wavelength are very high (ℜ → ∞ and αL >> 1). By applying the Fourier series analysis to the intensity of the laser beam and the temperature in the stationary regime of the laser heating [2,3], the complex temperature amplitude of the front face of a plate can be written as: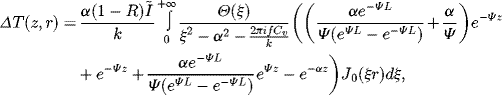 (1)with
(1)with 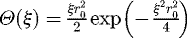 for the Gaussian beam;
for the Gaussian beam;  ;
; 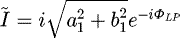 ;
; 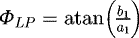 ;
; 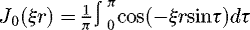 ;
; 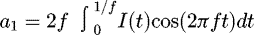 ;
; 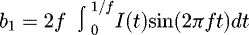 ;
; 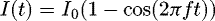 , where: z and r, respectively, are the propagation direction of the laser beam and the radial distance from the center of the heated zone at the sample surface; Cv, k and L: the volumetric specific heat, the thermal conductivity and the thickness of the sample; α and R: the laser absorption coefficient and the reflectivity of the sample surface; r0: the laser beam radius at 1/e intensity, I(t) and I0: the intensity of the laser beam and its amplitude; f, t and i: the repetitive rate frequency of the laser, the time and the complex unity; ξ and τ: the variables of the integration; ΦLP: the phase of the laser power.
, where: z and r, respectively, are the propagation direction of the laser beam and the radial distance from the center of the heated zone at the sample surface; Cv, k and L: the volumetric specific heat, the thermal conductivity and the thickness of the sample; α and R: the laser absorption coefficient and the reflectivity of the sample surface; r0: the laser beam radius at 1/e intensity, I(t) and I0: the intensity of the laser beam and its amplitude; f, t and i: the repetitive rate frequency of the laser, the time and the complex unity; ξ and τ: the variables of the integration; ΦLP: the phase of the laser power.
The phase shift between the laser and the thermal power can be found by the expression: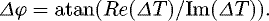 (2)
(2)
2.1 Environmental effect
The heat exchange with the environment by convection mechanism can be introduced by the conditions of limits at z = 0 and z = L [4]: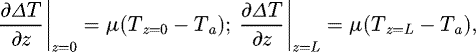 (3)where:
(3)where: 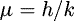 , h(Wm–2 K–1) is a coefficient of thermal exchange with environment by convection. The environment temperature Ta is supposed to be equal to the initial temperature of the plate, thus:
, h(Wm–2 K–1) is a coefficient of thermal exchange with environment by convection. The environment temperature Ta is supposed to be equal to the initial temperature of the plate, thus: 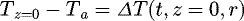 ;
; 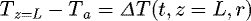 . The losses by thermal emission are supposed to be negligible.
. The losses by thermal emission are supposed to be negligible.
The solution of the heat equation: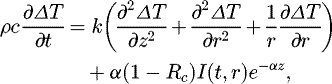 (4)on 0 ≤ z ≤ L with the initial condition
(4)on 0 ≤ z ≤ L with the initial condition 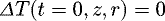 was obtained for the nth harmonic of the laser repetition frequency:
was obtained for the nth harmonic of the laser repetition frequency: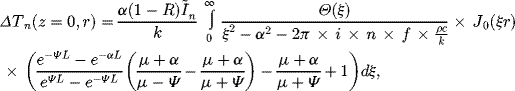 (5)where:
(5)where: 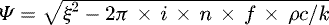 ;
; 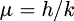 ;
;
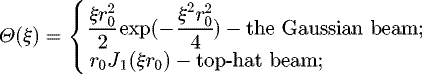
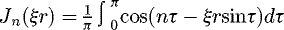 ;
; 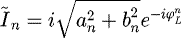 ;
;
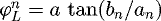 ;
; 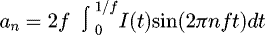 ;
;
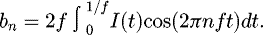
The phase shift can be written as: (6)
(6)
It depends on the parameters k, ρc, α, L, r0, h. For thin metal plates, the environmental effect on the phase shift may be considered as negligible. For example, for SS 304L of 400 μm thickness, the phase shifts are not affected by the environment even for a material with h = 100 W/m2 K (water) [4].
2.2 Simple analytical expressions
The numerical simulation of laser heating is used to fit the calculated phase shifts with the experimental ones by adjusting the material properties. A typical dependence of a phase shift on a laser modulation frequency is presented in Figure 2. For the laser beam with a diameter satisfying r0/100 ≤ L ≤ r0/2, one may observe a minimum on the phase shift curve with the corresponding values ϕmin and fmin.
Multiparameter simulation of laser heating enables one to determine the effect of the interaction parameters and the material properties on the phase shifts [3–7]. Two analytical expressions were derived to relate laser parameters, sample properties, ϕmin and fmin. This inter-relationship may provide rapid measurements of thickness L and diffusivity D of a sample with 99% accuracy: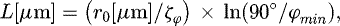 (7)
(7)
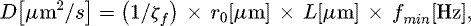 (8)with ζϕ and ζf calculated values (Fig. 3).
(8)with ζϕ and ζf calculated values (Fig. 3).
 |
Fig. 2 Phase shift for SS 304L plate of 400 μm thickness. |
 |
Fig. 3 Calculated values of ζϕ and ζf parameters. |
3 Experimental
The experimental setup with a compact fiber laser (low divergent near the Gaussian beam with M2 = 1.1, beam radius r0 ≅ 1 mm, 1060 nm wavelength) is simple in its arrangement (Fig. 4) and enables one to make remote measurements with a millimeter lateral resolution in a wide distance range (from some centimeters up to several meters).
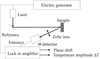 |
Fig. 4 Scheme of the experimental setup. |
3.1 Metal plates characterization
The lock-in thermography for a plate characterization was validated with a set of etalon samples. The obtained results on plate thickness and diffusivity measurements are presented in reference [3]. These results have demonstrated ≈90% accuracy of thickness and thermal diffusivity measurements. The measured thermal diffusivities along with the referenced values from literature are summarized in Figure 5.
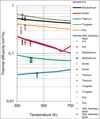 |
Fig. 5 Comparison of the measured thermal diffusivities along with the referenced values from literature (presented as solid lines) [8]. The square points – Dm2 and the circle points – Dm1 (see Tab. 1 for Dm definition). |
3.2 Zircaloy-4 cladding characterization
After the characterization of the metal plates by the above procedure, the method was used for studying Zircaloy-4 claddings (Fig. 6). The schematic comparison of the cladding diameter and the one of the heated zone (with the tested zone on it) is presented in Figure 6. As the heated zone diameter is smaller than the one of Zy4 cladding, the heated zone may be considered as a plane surface, and thus, the same procedure as the one for metal plates may be followed.
To study the effect of the oxide layer on the measured thermal diffusivity, some Zy4 claddings were artificially oxidized in a furnace at different regimes (temperature, environment, time) to obtain oxide layers of different thickness (5–15 μm). For 5 μm, 10 μm, and 15 μm oxide layer thickness, the regimes, respectively, were as follows: (500 °C, in air, for 37 hours), (550 °C, in air, for 23 hours), and (550 °C, in water vapor, for 51 hours). The surface of Zy4 with the oxide layer of 10 μm thickness has suffered nitriding effect, while the samples with 5 μm and 15 μm oxides were of a good quality.
The results on Zy4 claddings characterization are presented in Figures 7 and 8 and in Table 1. At low modulation frequency (f < 20 Hz), the phase shift is poorly affected by the presence of the oxide layer (Fig. 7). Thus, for Zircaloy-4 claddings, ϕmin and fmin method may be used to determine thickness and thermal diffusivity (see Tab. 1). The measurement relative deviations were less than 10%.
At higher modulation frequency (f > 20 Hz), a clear effect of the oxide layer on the phase shifts is observed (Fig. 7). Due to the fact that ZrO2 layers are semitransparent, the theoretical models for phase shift calculation [1,2] are not applicable in this case. However, there are all the reasons to suppose that further development of the thermal model of heating a semi-transparent layer on a metal plate will provide an adequate on-line in situ characterization of oxide formation.
 |
Fig. 6 On the left: schematic comparison of the Zy4 cladding diameter and those of the heated zone (in red) and of the tested zone on it (in blue). On the right: the picture of Zy4 claddings. Some Zy4 claddings were artificially oxidized (on the right in the picture). |
 |
Fig. 7 Phase shifts for Zy4 claddings as a function of modulated frequency. |
 |
Fig. 8 Measured and reference values of thermal diffusivity as a function of temperature (°C) for Zy4 claddings. |
Thickness and thermal diffusivity measurements for Zy4 claddings with oxide layers.
4 Conclusions
The homemade thermal model of the local heating of a homogeneous and isotropic plate with infinite dimensions was developed and verified by characterizing different metal plates and Zircaloy-4 claddings. Two analytical expressions (7) and (8) for sample thickness L and thermal diffusivity D were derived. These expressions and the lock-in thermography measurements (the minimal phase shift ϕmin and the corresponding minimal modulated frequency fmin [6,7]) are used to measure the thickness and the thermal diffusivity of the samples. The obtained results are in agreement with experimental data within an accuracy of 90%. The developed method may be applied for any material with a high absorption coefficient α, that is, for any plate with αL >> 1. Based on the results obtained, we may conclude that a rapid remote in situ control over components in nuclear installations may be ensured with a good spatial resolution (of the order of a laser beam diameter 2r0).
Acknowledgments
Authors acknowledge DEN/DANS/DMN/SRMA/LC2M team for Zircaloy-4 claddings supply.
References
- A. Semerok, F. Jaubert, S.V. Fomichev et al., Laser lock-in thermography for thermal contact characterisation of surface layer, Nucl. Instrum. Methods Phys. Res. A 693 , 98 (2012) [CrossRef] [Google Scholar]
- A. Semerok, S.V. Fomichev, F. Jaubert et al., Active laser pyrometry and lock-in thermography for characterisation of deposited layer on TEXTOR graphite tile, Nucl. Instrum. Methods Phys. Res. A 738 , 25 (2014) [CrossRef] [Google Scholar]
- S. Pham Tu Quoc, G. Cheymol, A. Semerok, New contactless method for thermal diffusivity measurements using modulated photothermal radiometry, Rev. Sci. Instrum. 85 , 054903 (2014) [CrossRef] [Google Scholar]
- S. Pham Tu Quoc, Caractérisation des propriétés d’un matériau par radiométrie photothermique modulée, CEA PhD Thesis, France, 2014 [Google Scholar]
- D. Melyukov, Étude et développement d’une méthode de caractérisation in-situ et à distance de dépôts en couches minces par pyrométrie active laser, CEA PhD Thesis, France, 2011 [Google Scholar]
- D. Melyukov, P.-Y. Thro, Patent CEA FR2980846-A1, Procédé de détermination sans contact de l’épaisseur d’un échantillon, 2013 [Google Scholar]
- S. Pham Tu Quoc, G. Cheymol, A. Semerok, Patent CEA FR1355905, Procédé de détermination de la diffusivité thermique et système pour la mise en œuvre, 2013 [Google Scholar]
- Y.S. Touloukian, R.W. Powell, C.Y. Ho, M.C. Nicolaou, Thermal diffusivity (IFI/Plenum, New York, 1973) [Google Scholar]
Cite this article as: Alexandre Semerok, Sang Pham Tu Quoc, Guy Cheymol, Catherine Gallou, Hicham Maskrot, Gilles Moutiers, Lock-in thermography for characterization of nuclear materials, EPJ Nuclear Sci. Technol. 2, 20 (2016)
All Tables
Thickness and thermal diffusivity measurements for Zy4 claddings with oxide layers.
All Figures
 |
Fig. 1 Phase shift of heating temperature. |
| In the text | |
 |
Fig. 2 Phase shift for SS 304L plate of 400 μm thickness. |
| In the text | |
 |
Fig. 3 Calculated values of ζϕ and ζf parameters. |
| In the text | |
 |
Fig. 4 Scheme of the experimental setup. |
| In the text | |
 |
Fig. 5 Comparison of the measured thermal diffusivities along with the referenced values from literature (presented as solid lines) [8]. The square points – Dm2 and the circle points – Dm1 (see Tab. 1 for Dm definition). |
| In the text | |
 |
Fig. 6 On the left: schematic comparison of the Zy4 cladding diameter and those of the heated zone (in red) and of the tested zone on it (in blue). On the right: the picture of Zy4 claddings. Some Zy4 claddings were artificially oxidized (on the right in the picture). |
| In the text | |
 |
Fig. 7 Phase shifts for Zy4 claddings as a function of modulated frequency. |
| In the text | |
 |
Fig. 8 Measured and reference values of thermal diffusivity as a function of temperature (°C) for Zy4 claddings. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


