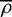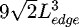| Issue |
EPJ Nuclear Sci. Technol.
Volume 2, 2016
|
|
|---|---|---|
| Article Number | 19 | |
| Number of page(s) | 7 | |
| DOI | https://doi.org/10.1051/epjn/2016013 | |
| Published online | 15 April 2016 | |
https://doi.org/10.1051/epjn/2016013
Regular Article
Modelling of as-fabricated porosity in UO2 fuel by MFPR code
Nuclear Safety Institute (IBRAE), Russian Academy of Sciences, 52, B. Tulskaya, 115191, Moscow, Russia
⁎ e-mail: tarasov@ibrae.ac.ru
Received:
3
October
2015
Accepted:
16
February
2016
Published online:
15
April
2016
For consistent modelling of behaviour of as-fabricated porosity in UO2 fuel irradiated under various conditions of in-pile and out-of-pile tests as well as under normal and abnormal conditions of nuclear reactor operation, the additional analysis of experimental observations and critical assessment of available models are presented. On this base, the mechanistic MFPR code, including physically-grounded models for the fuel porosity evolution in UO2 fuel under various irradiation and thermal regimes, is refined. These modifications complete the consistent description of the fuel porosity evolution in the MFPR code and result in a notable improvement of the code predictions.
© V.I. Tarasov and M.S. Veshchunov, published by EDP Sciences, 2016
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The in-pile dimensional behaviour of oxide fuels in nuclear reactors is a well-known phenomenon of great technological interest. It is generally established that at the beginning of irradiation the fuel densifies due to shrinking of the as-fabricated pores remaining from the fuel sintering process with a wide distribution of their sizes [1,2]. The densification is most pronounced in low density fuel, especially in the case of fine-dispersed porosity with pores typically less than one micron diameter.
Re-sintering in the furnace can be generally understood and described analytically by thermal diffusion processes, but not so in-pile densification: it was additionally assumed by Stehle and Assmann [3] that in-pile densification is a mixed athermal/thermal process, including the thermal evaporation of vacancies from pores (which dominates at relatively high temperatures above ≈1200 °C), and the athermal atomization of pores into lattice vacancies by fission spikes.
For consistent modelling of porosity behaviour in UO2 fuel irradiated under various conditions of in-pile and out-of-pile tests as well as under normal and abnormal conditions of nuclear reactor operation, the critical assessment of available models, their modification and development of more advanced models for implementation in the mechanistic codes, become rather an important task. The code MFPR (Module for Fission Products Release) was developed for analysis of fission products (FP) release from irradiated UO2 fuel in collaboration between IBRAE and IRSN (Cadarache, France) [4,5]. The mechanistic approach applied in this code allows the realistic consideration of fuel porosity evolution, self-consistently with analysis of FP release, based on physically-grounded parameters and mechanisms.
Some important modifications of the existing models of MFPR and development of new models for the fuel porosity evolution in UO2 fuel under various irradiation and thermal regimes are presented in this paper.
2 Initial fuel porosity
Optical microscopy reveals that the majority of the internal cavities are located on grain boundaries [6]; the pores are generally non-spherical in shape. In the current analysis, the pores are considered as intergranular lenticular voids with the dihedral angle θ = 50°. Their volume, V, and surface area, S, are [7]: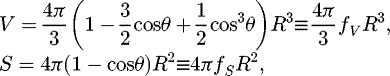 (1)where the pore curvature radius, R, relates to the experimentally measured median radius, ρ (which below will be simply referenced to as ‘radius’) as:
(1)where the pore curvature radius, R, relates to the experimentally measured median radius, ρ (which below will be simply referenced to as ‘radius’) as: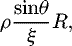 (2)where
(2)where 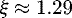 (see Appendix A of Ref. [8]).
(see Appendix A of Ref. [8]).
In the typical fresh fuel, the pores sizes are distributed within the interval 0.1–10 μm, their density distribution function can be satisfactory approximated as [8]: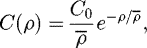 (3)where C0 is the total pore concentration and
(3)where C0 is the total pore concentration and 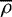 is the mean radius. The maximum contribution to the total porosity makes pores with
is the mean radius. The maximum contribution to the total porosity makes pores with  .
.
Figure 1 illustrates approximations of the experimental distributions observed in reference [9] for normal grain (mean grain diameter dgr = 8 μm) and large grain (23 μm) samples. The normal grain data are approximated by equation (3) with the mean radius of 0.35 μm and total porosity of 4.7%. Note that pores with ρ from 0.5 to 2 μm contribute near 75% to the total porosity. The large grain data are approximated by a superposition of two exponents corresponding to two pore populations, P1 and P2, with the mean radii of 0.45 and 3.0 μm, the partial porosities being 1.2 and 4.3% respectively.
 |
Fig. 1 Initial pore size distributions in fuel samples of the Harada and Doi test [9] and their approximations. |
3 Mechanisms of pore size relaxation
If the grain boundary self-diffusion is the rate controlling mechanism of the thermal pore relaxation, the pore volume change is described by the equation [10,11]: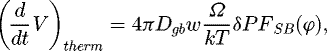 (4)where Dgb is the grain boundary diffusivity, w ≈ 0.5 nm is the thickness of the grain boundary layer, Ω = 4.09 × 10–29 m3 is the atomic volume, k is the Boltzmann constant, T is the temperature. The pressure difference, δP, is given by equation:
(4)where Dgb is the grain boundary diffusivity, w ≈ 0.5 nm is the thickness of the grain boundary layer, Ω = 4.09 × 10–29 m3 is the atomic volume, k is the Boltzmann constant, T is the temperature. The pressure difference, δP, is given by equation: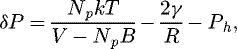 (5)where Np is the number of gas atoms in the pore, Ph is the external pressure, B is the van der Waals constant, ϕ is the fractional coverage of the grain boundary by pores.
(5)where Np is the number of gas atoms in the pore, Ph is the external pressure, B is the van der Waals constant, ϕ is the fractional coverage of the grain boundary by pores.
The factor FSB was derived in reference [10] for the case of small identical pores uniformly distributed over an infinitely large grain boundary, if the vacancy diffusion in the grain boundary is rate controlling: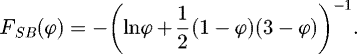 (6)
(6)
This function is of order of 1 for typical ϕ values of 10–20%, however it has logarithmic singularity at ϕ→0 and cubic singularity at ϕ→1. Moreover, applicability of equation (6) is unclear in the case of ensemble of different pores as well as in the case of large pores, which size is comparable with inter-pore distance or with grain face size. Therefore, for simplification it was assumed in this paper that FSB = 1.
As for the grain boundary diffusivity, considerable uncertainty still exists in the literature. It was shown in reference [8] that the best fit to the re-sintering data of references [9] and [12] is provided by the Arrhenius correlation for the diffusivity with parameters of Reynolds and Burton [13]. For instance, simulations of the re-sintering conditions (24 h at 1700 °C) in the Harada and Doi test resulted in the density change of 1.15% for the normal grain and 0.175% for the large grain samples (including reduction by 0.173% for population P1 and 0.002% for P2), which should be compared with the experimental values of 1.08% and 0.19% [9].
Dollins and Nichols [10], following Stehle and Assmann [3], concluded that the thermal vacancy emission alone is not sufficient to explain the healing of pores under irradiation, especially at low temperatures. This is illustrated in Figure 2 where the results are presented of simulation of porosity evolution with equation (4) under steady irradiation conditions in the Harada and Doi test (the line denoted as ‘thermal’). In these calculations, the mean pellet temperature was supposed to be equal to 1100 K, in accordance with reference [9].
To overcome this difficulty, the irradiation-induced vacancy knock-out mechanism was introduced in references [3,10]: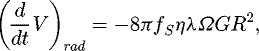 (7)where η is the number of vacancies that escape the pore per each hit, λ ∼ 1 μm is the “viable” track length of the fission fragment, and G is the fission rate. As for the key parameter, η, the authors referenced the value of 600 deduced from the fuel sputtering experiments [14]; however, they considered this value as the upper limit and set η = 100. Note for comparison that in the subsequent sputtering experiments [15] the value of η ∼ 20 was observed at typical stopping power of 20 keV/nm.
(7)where η is the number of vacancies that escape the pore per each hit, λ ∼ 1 μm is the “viable” track length of the fission fragment, and G is the fission rate. As for the key parameter, η, the authors referenced the value of 600 deduced from the fuel sputtering experiments [14]; however, they considered this value as the upper limit and set η = 100. Note for comparison that in the subsequent sputtering experiments [15] the value of η ∼ 20 was observed at typical stopping power of 20 keV/nm.
The above equation (7) has a trivial solution: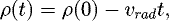 (8)where
(8)where 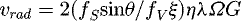 . With η = 100 and typical fission rate of 1019 m–3 s–1, this parameter equals to ≈10–13 m/s, so that the pores with ρ < 10 μm would disappear during standard LWR campaign. With the initial exponential pore size distribution, equation (3), the total fuel porosity decays exponentially:
. With η = 100 and typical fission rate of 1019 m–3 s–1, this parameter equals to ≈10–13 m/s, so that the pores with ρ < 10 μm would disappear during standard LWR campaign. With the initial exponential pore size distribution, equation (3), the total fuel porosity decays exponentially: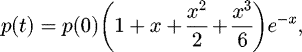 (9)where
(9)where 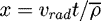 . In particular, this equation predicts decrease of the initial porosity in the typical LWR fuel by an order of magnitude at burnup of 1 GWd/t, which is considerably faster than the experimental observations. Even if to decrease the parameter η down to 20, the kinetics of fuel densification remains strongly overestimated (the curves ‘Dollins & Nichols’ in Fig. 2).
. In particular, this equation predicts decrease of the initial porosity in the typical LWR fuel by an order of magnitude at burnup of 1 GWd/t, which is considerably faster than the experimental observations. Even if to decrease the parameter η down to 20, the kinetics of fuel densification remains strongly overestimated (the curves ‘Dollins & Nichols’ in Fig. 2).
In particular, equation (7) does not predict the saturation of the densification process, which can be explained considering that pores with the size greater than some threshold value do not shrink, the threshold being associated with the grain size [16]. Therefore, to take into account this threshold effect, the cut-off of the irradiation term was suggested in reference [8], which can be implemented in equation (7) in the smoothed form: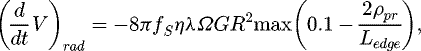 (10)where ρpr is the pore projection radius and Ledge ≈ 0.69Rgr is the typical length of the grain edge1. With the choice η = 50, this allows reasonably reproducing not only the experimental correlation [9] for the densification kinetics, Figure 2 (curve ‘modified’), but also the kinetics of the total fuel density due to both pores and inter- and intragranular fission gas bubbles, measured in references [17,18] and presented in reference [9] (Fig. 3).
(10)where ρpr is the pore projection radius and Ledge ≈ 0.69Rgr is the typical length of the grain edge1. With the choice η = 50, this allows reasonably reproducing not only the experimental correlation [9] for the densification kinetics, Figure 2 (curve ‘modified’), but also the kinetics of the total fuel density due to both pores and inter- and intragranular fission gas bubbles, measured in references [17,18] and presented in reference [9] (Fig. 3).
 |
Fig. 2 Simulation of fuel porosity under irradiation in the Harada and Doi test [9] with the thermal relaxation term, equation (4), and different variants of the irradiation term, equation (7); markers correspond to the experimental correlation [9], ‘modified’ corresponds to equation (10). |
 |
Fig. 3 Kinetics of the fuel density calculated by MFPR for normal grain samples. |
4 Fission gas capture by pores
The initial number of gas atoms in pores per one grain can be evaluated as: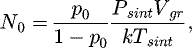 (11) where p0 is the initial porosity, Tsint and Psint are the temperature and pressure during fuel sintering. The total number of gas atoms, Nrel, released from one grain during reactor campaign is equal to κbfgVgr, where κ ≈ 0.3 is the fission gas yield per one fission, fg is the fractional release of the gas atoms to the grain boundaries and b is the burnup (number of fissions per unit volume). Therefore, one evaluates that:
(11) where p0 is the initial porosity, Tsint and Psint are the temperature and pressure during fuel sintering. The total number of gas atoms, Nrel, released from one grain during reactor campaign is equal to κbfgVgr, where κ ≈ 0.3 is the fission gas yield per one fission, fg is the fractional release of the gas atoms to the grain boundaries and b is the burnup (number of fissions per unit volume). Therefore, one evaluates that: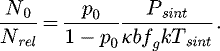 (12)
(12)
For the typical values Tsint = 2000 K, Psint = 105 Pa, b = 1027 m–3 and fg = 0.1, one evaluates this ratio as 0.6% (whereas the ratio of N0 to the total generated gas is an order of magnitude less than this estimate).
The pores can capture the fission gas escaping from fuel grains. The capture rate is estimated multiplying the pore area, equation (1), by the gas flux density, Φ: (13)where the gas flux density can be found as the time derivative of the number of gas atoms released from the grain per unit area of grain surface:
(13)where the gas flux density can be found as the time derivative of the number of gas atoms released from the grain per unit area of grain surface: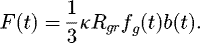 (14)
(14)
In the case of constant fission rate, b (t) = Gt and thus: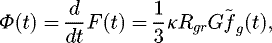 (15)where
(15)where 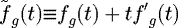 . At the beginning of irradiation
. At the beginning of irradiation 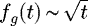 , so
, so 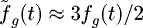 , whereas in the case of high burnup
, whereas in the case of high burnup 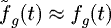 .
.
On the other hand, the gas atoms can be knocked out from pores by passing fission fragments (irradiation-induced resolution). Following Nelson's model [19], the resolution rate for intergranular pores is estimated in MFPR as [20]: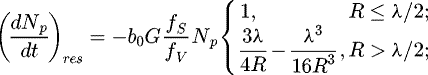 (16)where b0 is the resolution constant, λ is the average distance the ejected atom travels in pore, δ is the width of the resolution layer [19]. As explained in reference [21], the original Nelson model is used for intergranular porosity without modifications, suggested in reference [22] for intragranular bubbles (in order to avoid duplication of the backward flux of atoms, struck from pores, to the grain boundary).
(16)where b0 is the resolution constant, λ is the average distance the ejected atom travels in pore, δ is the width of the resolution layer [19]. As explained in reference [21], the original Nelson model is used for intergranular porosity without modifications, suggested in reference [22] for intragranular bubbles (in order to avoid duplication of the backward flux of atoms, struck from pores, to the grain boundary).
5 Qualitative analysis
At the beginning of irradiation, the pores are generally under-compressed so that they tend to shrink due to both thermal and irradiation mechanisms, equations (4) and (10). As a result the internal gas pressure in pores increases and eventually the pressure difference δP, equation (5), approaches zero. Neglecting the van der Waals correction (required for small bubbles with R < 5 μm), one derives the relationship between the number of gas atoms in pore Neq and its curvature radius at equilibrium Req: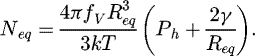 (17)
(17)
In the limiting cases one estimates the resolution term, equation (16), as: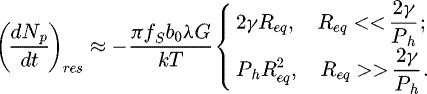 (18)
(18)
Therefore, one gets estimates for the rhs of the complete equation for Np in the equilibrium: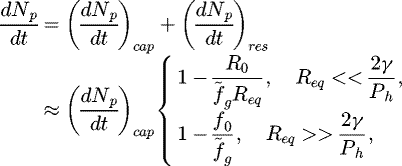 (19)where R0, and f0 are the constants depending on the model parameters and external conditions:
(19)where R0, and f0 are the constants depending on the model parameters and external conditions: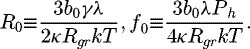 (20)
(20)
For the typical parameter values Rgr = 5 μm and T = 1100 K, one evaluates that R0 ≈ 7.6 μm, f0 ≈ 3.2. It follows from these estimates for small pores (which quickly equilibrate so that 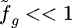 ) that
) that 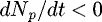 , therefore after equilibration small pores definitely lose the gas and hence continue shrinking. The same conclusion can be drawn for large equilibrated pores; however, with less reliability in view of uncertainties of the resolution model and the relevant parameters. Therefore, one expects that pores of all sizes lose their gas after equilibration. The opposite trend cannot be excluded under some extreme conditions (high burnups at high temperature of the large grain fuels). Note that these conclusions were drawn for the equilibrated pores whereas the gas content in non-equilibrium pores can be either reducing or growing.
, therefore after equilibration small pores definitely lose the gas and hence continue shrinking. The same conclusion can be drawn for large equilibrated pores; however, with less reliability in view of uncertainties of the resolution model and the relevant parameters. Therefore, one expects that pores of all sizes lose their gas after equilibration. The opposite trend cannot be excluded under some extreme conditions (high burnups at high temperature of the large grain fuels). Note that these conclusions were drawn for the equilibrated pores whereas the gas content in non-equilibrium pores can be either reducing or growing.
6 Quantitative analysis
The above qualitative considerations are illustrated in Figure 4 by MFPR numerical simulations of evolution of pores with initial radii of 0.1, 1 and 10 μm (curves labelled in the graph as 1, 2 and 3, respectively) under irradiation conditions of the Harada and Doi test [9]: normal grain fuel (dgr = 8 μm) with the initial porosity of 4.7% under temperature of 1100 K, pressure of 3 MPa and fission rate of 1019 m–3 s–1; the initial pore distribution was approximated by equation (3) with 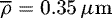 .
.
It is seen that the relatively small pores quickly equilibrate, monotonically shrink and eventually disappear (equilibration times are ∼6 × 105, 5 × 106 and 5 × 107 s for pores with the initial radii of 0.1, 0.3 and 1 μm). The large pores (≥ 3 μm) are practically unchanged in their sizes. The final fuel porosity averaged over the pore ensemble turned out to be 2.8%.
As for the gas content, it monotonically decreases in small pores (ρ ≤ 0.5 μm in these calculations) because the resolution mechanism dominates in the initial stage of irradiation when the small pores effectively shrink, e.g. see curve 1 in the right panel. For the larger pores, Np(t) can be non-monotonic function, however it finally decreases (at least after equilibration, see previous Sect. 5), e.g. curve 2. The gas content in pores with ρ > 1.2 μm increases to the end of irradiation in comparison with the initial value; however these pores remain under-pressurized (curve 3). The maximum relative gas increase (∼37%) is attained in pores with the initial radius of 2 μm. As for the overall gas content in the pore ensemble, first it rapidly decreased by a factor of ∼15 at burnup of ≈3 GWd/t and then slowly increased; the gas content was near 80% of the initial value to the end of the campaign (54 GWd/t); this change can be estimated using equation (12) as ∼0.1% of the gas released from the fuel grains.
To clarify the role of gas capture/resolution effects, the calculations were repeated with fixed Np (dashed curves in Fig. 4). It is seen on the left panel that the solid and dashed curves are very close to each other except of the stage of quick shrinking. However, at this stage the volumes of the pores are much less in comparison with the initial values and hence do not essentially contribute to the fuel porosity. As for the large pores, their sizes are practically constant, so the two approaches are close to each other too. In addition, the contribution of the largest pores to the total porosity is exponentially small (it can be evaluated by Eq. (9) with 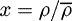 ). These qualitative considerations were confirmed by our calculations which showed that the gas capture/resolution effect influenced the final porosity by ≈0.01% only.
). These qualitative considerations were confirmed by our calculations which showed that the gas capture/resolution effect influenced the final porosity by ≈0.01% only.
These calculations demonstrated that the pores cannot be considered as effective traps of the fission gas released from the nuclear fuel. In addition, it was justified that the neglect of gas content variation in pores is a good approximation in numerical calculations, as qualitatively discussed in reference [8]. To check these conclusions, the additional calculations have been performed with the same initial pore distribution but varying one of the external parameters: grain size, fission rate or irradiation temperature. In all these cases, the pore kinetics were found to be qualitatively similar to that presented in Figure 4.
Simulations with the increased fission rate (5 × 1019 m–3 s–1) have shown that an increase of the overall gas content (following a fast initial decrease by a factor of 8) resulted in full compensation of the gas content in pores at burnup of 75 GWd/t. These variations were within 0.1% of the gas amount released from the grains, which is comparable with the above considered cases. The gas capture/resolution mechanisms were found to contribute to the final fuel porosity (which was equal to 2.33%) very similarly to the above examples. The greatest differences were found in calculations with the increased temperature. At T = 1500 K, the initial decrease of the gas content was followed (at burnup of ≈1 GWd/t) by a slight increase, which in turn followed again (at ≈4 GWd/t) by decrease up to the end of the campaign; the final content was found to be of 16% of the initial value. In addition, the simulations of the fuel volume evolution (including both pores and fission gas bubbles) under irradiation conditions of the Harada and Doi test [9] were performed (Fig. 5). The following external conditions were chosen: the mean irradiation temperature 1100 K, fission rate 1019 m–3 s–1, and external pressure 3 MPa. In the case of the large grain fuel, the realistic bi-modal initial pore size distribution was simulated as superposition of P1 and P2 populations, see Section 2.
It was found that the pore populations P1 and P2 lost 84% and 1.4% of their initial volume respectively so that the total pore densification turned out to be of 1.07%. The final fuel density change (at the burnup of 21 GWd/t) was estimated as –1.5% and –0.9% for the normal and large grain fuels respectively. Comparison with the experiment [9] demonstrates good agreement for the very initial stages of irradiation (up to ∼1 and 3 GWd/t for the large and normal grain fuels respectively). However, in later stages there is a qualitative difference in the fuel volume variation kinetics. Moreover, the similar disagreement takes place between the experimental data in reference [9] and references [17,18], also cf. Figure 3. The authors of reference [9] supposed that the discrepancy could be caused by “fuel fragment relocation at the early stage of the irradiation”. This effect was not simulated in our calculations, but is foreseen in the forthcoming version of the code. Besides, for large grain samples a more detailed experimental information is required on pore size distribution in grains of different sizes (rather than available averaged data presented in Fig. 1), since the real grain size distribution is rather flat (see Ref. [9]) and this may strongly influence the threshold sizes for shrinking pores in equation (10).
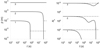 |
Fig. 4 Time dependence of pore radii and gas atom content in pores under irradiation conditions of the test [9]; dashed lines correspond to calculations with Np = const. |
 |
Fig. 5 Kinetics of fuel volume change under irradiation for the large and normal grain samples. |
7 Conclusions
The MFPR model for intergranular pore evolution was updated and verified against experimental data [9,17,18], and then applied to analysis of the sintering porosity behaviour under various conditions of in-pile irradiation.
The performed analysis demonstrated that generally the resolution of gas atoms from pores prevails over capture of the fission gas released from grains in early stages of irradiation, which somewhat accelerates fuel densification. In later stages, the gas content of the survived large pores can increase, but not significantly. As a result, pores lose their gas content during typical reactor campaign; however the effect being vanishingly small. This implies that pores can be hardly considered as effective traps for the fission gas.
The model predicts a comparatively rapid fuel densification due to shrinkage of small pores with projection radius less or comparable with the grain face size, whereas the coarse pores remain unchanged, in agreement with numerous observations, e.g. references [6,16]. In particular, this implies that the second population of relatively large pores in fuel with large grains, fabricated with a pore former, provides a rather small densification (mainly due to the first population of small pores) and thus can be hardly used for accommodation of the fuel swelling. At high burnups this can result in significant pellet-cladding mechanical interaction caused from the swelling due to retained gases and solid FPs. However, this preliminary conclusion should be thoroughly verified against additional experimental data.
Nomenclature
b : burnup (number of fissions per unit volume)
B : van der Waals volume of the gas atom
C (ρ): pore size distribution function normalized to the pore concentration
Dgb : grain boundary self-diffusivity
fg : fission gas fractional release
G : fission rate (number of fissions in unit volume per unit time)
Np : number of gas atoms in pore
η : mean number of vacancies knocked out from pore per one hit
ϕ : fractional coverage of the grain boundary by pores
Φ : fission gas out-of-grain flux density
References
- M.D. Freshley, D.W. Brite, J.L. Daniel, P.E. Hart, Irradiation-induced densification of UO2 pellet fuel, J. Nucl. Mater. 62 , 138 (1976) [CrossRef] [Google Scholar]
- G. Maier, H. Assmann, W. Dorr, Resinter testing in relation to in-pile densification, J. Nucl. Mater. 153 , 213 (1988) [CrossRef] [Google Scholar]
- H. Stehle, H. Assmann, The dependence of in-reactor UO2 densification on temperature and microstructure, J. Nucl. Mater. 52 , 303 (1974) [CrossRef] [Google Scholar]
- M.S. Veshchunov, V.D. Ozrin, V.E. Shestak, V.I. Tarasov, R. Dubourg, G. Nicaise, Development of mechanistic code MFPR for modelling fission product release from irradiated UO2 fuel, Nucl. Eng. Des. 236 , 179 (2006) [CrossRef] [Google Scholar]
- M.S. Veshchunov, R. Dubourg, V.D. Ozrin, V.E. Shestak, V.I. Tarasov, Mechanistic modeling of urania fuel evolution and fission product migration during irradiation and heating: the MFPR code, J. Nucl. Mater. 362 , 327 (2007) [CrossRef] [Google Scholar]
- B. Burton, G.L. Reynolds, The sintering of grain boundary cavities in uranium dioxide, J. Nucl. Mater. 45 , 10 (1972) [CrossRef] [Google Scholar]
- R.J. White, M.O. Tucker, A new fission-gas release model, J. Nucl. Mater. 118 , 1 (1983) [CrossRef] [Google Scholar]
- V.I. Tarasov, M.S. Veshchunov, Models for fuel porosity evolution in UO2 under various regimes of reactor operation, Nucl. Eng. Des. 272 , 65 (2014) [CrossRef] [Google Scholar]
- Y. Harada, S. Doi, Irradiation behavior of large grain UO2 fuel rod by active powder, J. Nucl. Sci. Tech. 35 , 411 (1998) [CrossRef] [Google Scholar]
- C.C. Dollins, F.A. Nichols, In-pile intragranular densification of oxide fuels, J. Nucl. Mater. 78 , 326 (1978) [CrossRef] [Google Scholar]
- M.V. Speight, W. Beere, Vacancy potential and void growth on grain boundaries, Metal Sci. 9 , 190 (1975) [CrossRef] [Google Scholar]
- G. Maier, H. Assmann, W. Dorr, Resinter testing in relation to in-pile densification, J. Nucl. Mater. 153 , 213 (1988) [CrossRef] [Google Scholar]
- G.L. Reynolds, B. Burton, Grain-boundary diffusion in uranium dioxide: The correlation between sintering and creep and a reinterpretation of creep mechanism, J. Nucl. Mater. 82 , 22 (1979) [CrossRef] [Google Scholar]
- S. Yamagishi, T.J. Tanifuji, Post-irradiation studies on knock-out and pseudo-recoil releases of fission products from fissioning UO2, J. Nucl. Mater. 59 , 243 (1976) [CrossRef] [Google Scholar]
- S. Schlutig, Contribution à l’étude de la pulvérisation et de l’endommagement du dioxyde d’uranium par les ions lourds rapides, PhD Thesis, University of Caen, 2001 [Google Scholar]
- M.O. Marlowe, In-reactor densification behavior of UO2, NEDO-12440, 1973 [Google Scholar]
- Y. Irisa, Y. Takada, in ANS Topical Meeting , Williamsburg (1988) [Google Scholar]
- S. Doi, S. Abeta, Y. Irisa, S. Inoue, in ANS Topical Meeting , Avignon, France (1991) [Google Scholar]
- R.S. Nelson, The stability of gas bubbles in an irradiation environment, J. Nucl. Mater. 31 , 153 (1969) [CrossRef] [Google Scholar]
- V.I. Tarasov, M.S. Veshchunov, An advanced model for grain face diffusion transport in irradiated UO2 fuel. Part 2. Model Implementation and validation, J. Nucl. Mater. 392 , 84 (2009) [CrossRef] [Google Scholar]
- M.S. Veshchunov, V.I. Tarasov, An advanced model for grain face diffusion transport in Irradiated UO2 fuel. Part 1. Model formulation, J. Nucl. Mater. 392 , 78 (2009) [CrossRef] [Google Scholar]
- M.S. Veshchunov, V.I. Tarasov, Modelling of irradiated UO2 fuel behaviour under transient conditions, J. Nucl. Mater. 437 , 250 (2013) [CrossRef] [Google Scholar]
Cite this article as: Vladimir I. Tarasov, Mikhail S. Veshchunov, Modelling of as-fabricated porosity in UO2 fuel by MFPR code, EPJ Nuclear Sci. Technol. 2, 19 (2016)
All Figures
 |
Fig. 1 Initial pore size distributions in fuel samples of the Harada and Doi test [9] and their approximations. |
| In the text | |
 |
Fig. 2 Simulation of fuel porosity under irradiation in the Harada and Doi test [9] with the thermal relaxation term, equation (4), and different variants of the irradiation term, equation (7); markers correspond to the experimental correlation [9], ‘modified’ corresponds to equation (10). |
| In the text | |
 |
Fig. 3 Kinetics of the fuel density calculated by MFPR for normal grain samples. |
| In the text | |
 |
Fig. 4 Time dependence of pore radii and gas atom content in pores under irradiation conditions of the test [9]; dashed lines correspond to calculations with Np = const. |
| In the text | |
 |
Fig. 5 Kinetics of fuel volume change under irradiation for the large and normal grain samples. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.