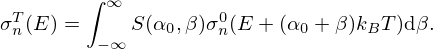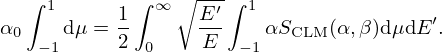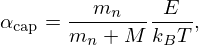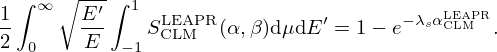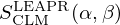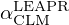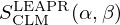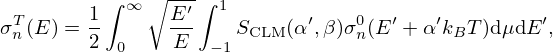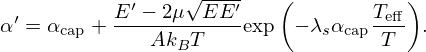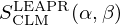| Issue |
EPJ Nuclear Sci. Technol.
Volume 11, 2025
|
|
|---|---|---|
| Article Number | 34 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/epjn/2025032 | |
| Published online | 17 July 2025 | |
https://doi.org/10.1051/epjn/2025032
Regular Article
Doppler broadening of neutron elastic scattering cross section using SCLM(α,β) thermal scattering laws
CEA, DES, IRESNE, DER, Cadarache F-13108 Saint Paul Les Durance France
* e-mail: gilles.noguere@cea.fr
Received:
18
January
2025
Received in final form:
23
April
2025
Accepted:
26
May
2025
Published online: 17 July 2025
In nuclear data processing codes, Free Gas and Crystal Lattice Models are used to account for temperature effects in neutron elastic scattering cross sections. A somewhat arbitrary thermal cutoff energy is introduced to define the energy ranges of application of the two models, given that the Crystal Lattice Model in processing codes can only be applied to constant cross sections. Despite works performed on 238U, no algorithm reported in the literature provides a unified Crystal Lattice Model valid below and above the thermal cutoff energy. This paper presents two new Doppler models, namely α0 and α′ models. The α0 model is able to account for the Doppler broadening effects in the resonance range of the neutron cross sections, while the α′ model provides a unified description of the Doppler effect over the entire energy range of interest for nuclear reactor applications. The performances of the models are illustrated with 238U, 240Pu and 237Np.
© A. Bengoechea Fernández et al., Published by EDP Sciences, 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The temperature of the target material impacts the shape of angle-integrated neutron cross-sections as a function of neutron energies. In the resonance range, the natural width of the resonances is broadened with the temperature increase, while the peak cross section decreases due to the thermal agitation of the target nucleus. This phenomenon is known as the Doppler broadening effect. In nuclear data processing codes, such as NJOY [1], temperature effects in neutron cross sections are mainly taken into account via two popular models. Above the so-called thermal cutoff energy of about a few electronvolts, the Doppler broadening of the angle-integrated neutron cross sections are routinely performed in the framework of the Free Gas Model (FGM). Below the thermal cutoff energy, Crystal Lattice Models (CLM) have to be used to account for the structure of the materials and the dynamics of the constituent atoms.
A few works have been performed on 238U [2–5], in order to extend the use of Crystal Lattice Models well above the thermal cutoff energy. Thanks to these works, Crystal Lattice Models are available in some resonance analysis codes, such as REFIT [6], SAMMY [7], and CONRAD [8]. However, these codes only cover the resonance range of the neutron cross sections and cannot reproduce the contribution of the inelastic scattering below the thermal cutoff energy. This issue is a strong limitation for nuclei having low lying resonances. As shown in Figure 1, the two models smoothly converge at the thermal cutoff energy of about 4 eV in the case of 238U in UO2, because the first s-wave resonance of 238U is located at 6.67 eV. In the case of 240Pu in PuO2, the discontinuity observed at 0.26 eV, due to the presence of the broad 240Pu resonance at 1.05 eV, is not valid. This paper aims to propose a suitable Doppler algorithm to overcome such a limitation in the case of the neutron elastic scattering cross section.
 |
Fig. 1. 238U in UO2 (a) and 240Pu in PuO2 (b) neutron scattering cross sections calculated at 294 K by using the Free Gas Model (FGM) and Crystal Lattice Model (CLM) of the NJOY processing code [1]. The thermal cutoff energies are equal to 4 eV and 0.26 eV, respectively. The SIGMA1 algorithm is used for FGM, and the LEAPR module is used for CLM. |
The proposed algorithm relies on SCLM(α,β) thermal scattering laws which contain the dynamical structure factors of the materials. It was developed to fulfil the following conditions. Below the thermal cutoff energy, the algorithm should reproduce the incoherent inelastic scattering cross section calculated with 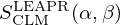 tables generated with the LEAPR module of NJOY. Above the thermal cutoff energy, it has to reproduce the Doppler broadened cross sections calculated with the Crystal Lattice Model implemented in the nuclear data code SAMMY [7]. The algorithm outputs will also be compared to Free Gas Model results computed with the SIGMA1 algorithm of NJOY because at high temperatures Free Gas and Crystal Lattice Models should provide nearly equivalent results.
tables generated with the LEAPR module of NJOY. Above the thermal cutoff energy, it has to reproduce the Doppler broadened cross sections calculated with the Crystal Lattice Model implemented in the nuclear data code SAMMY [7]. The algorithm outputs will also be compared to Free Gas Model results computed with the SIGMA1 algorithm of NJOY because at high temperatures Free Gas and Crystal Lattice Models should provide nearly equivalent results.
The Free Gas Model approximation and the theoretical framework of the Crystal Lattice Models are presented in Section 2. Section 3 focuses on the importance of the recoil energy of the target nucleus. Section 4 highlights the asymptotic form of the average dimensionless momentum transfer over the neutron resonance range of the elastic cross sections. Finally, Section 5 proposes a unified Doppler broadening model valid in the thermal and resonance ranges. Results are exemplified on 238U in UO2, 240Pu in PuO2 and 237Np in NpO2.
2. Doppler broadening models
In the framework of this work, we have distinguished two Doppler models: the Free Gas Model (FGM) and the Crystal Lattice Model (CLM). It is worth mentioning that the “Crystal Lattice Model” is a generic denomination covering various models reported in the literature. In this section, we restrict ourselves to the Crystal Lattice Model implemented in the LEAPR module of NJOY, whose analytical formulation can only be applied to constant neutron cross sections, in contrast to the Free Gas Model, which can also be applied to energy-dependent neutron cross sections. For the sake of clarity, we also restrict the presentation of the two formalisms to the elastic scattering cross section 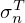 , where T represents the temperature of the target material. With this notation,
, where T represents the temperature of the target material. With this notation, 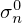 stands for the zero Kelvin cross section.
stands for the zero Kelvin cross section.
2.1. Free Gas Model for energy dependent neutron cross sections
In the Free Gas Model approximation, the Doppler broadened cross section at a given temperature T is calculated by averaging the zero Kelvin cross section over the target velocity distribution:
in which v is the velocity of the incident neutron, vr is the relative velocity between the neutron and the moving target nucleus, and ω(V) is the spectrum of the target velocities given by a Maxwell Boltzmann velocity distribution:
where kB is the Boltzmann constant, V is the velocity of the target nucleus and M is the mass of the target nucleus.
Equation (1) can be reduced to a convolution of the zero Kelvin cross section with a transfer function SFGM(E,E′,T) which depends on the temperature T, incident neutron energy E and outgoing neutron energy E′:
According to Ref. [7], the transfer function of the Free Gas Model, known as the Solbrig's kernel [9], is given by:
in which the Doppler width Δ depends on the neutron mass mn, target mass M, temperature T and incident neutron energy E:
For weakly bound crystals, the thermodynamic temperature T is not able to take into account the vibrational dynamics or the atom binding effects of the material, so Lamb proposed to replace the thermodynamic temperature with an effective temperature Teff [10]:
where ɛ=ℏω represents the energy transfer and ρ(ɛ) is the partial phonon density of states of the scattering atom in the material. Examples of partial phonon densities of states for 238U in UO2 at 300 and 1474 K are shown in Figure 2. By using these phonon densities of states, Equation (6) provides the following effective temperatures: Teff=317 K for T=300 K and Teff=1476 K for T=1474 K. Throughout the text, Free Gas Model calculations will be performed by introducing the effective temperature instead of the thermodynamic temperature T.
 |
Fig. 2. Partial phonon densities of states of 238U in UO2 at 300 and 1474 K deduced from inelastic neutron scattering experiments carried out at the Institute Laue-Langevin [12]. |
2.2. Crystal Lattice Model for constant neutron cross sections
Below the thermal cutoff energy, the neutron elastic scattering cross section is the sum of three cross sections: inelastic scattering, coherent elastic scattering and incoherent elastic scattering. In this work, we only consider the inelastic scattering contribution because it corresponds to the energy exchange between the neutron and the scattering atom. According to Ref. [1], the angle-integrated neutron inelastic scattering is calculated by:
where E (E′) is the incident (outgoing) neutron energy and μ=cos(θ) is the cosine of the scattering angle θ in the laboratory system. For a constant neutron elastic scattering cross section, the double-differential cross section formulated by Van Hove can be written as follows [11]:
where σp is the characteristic bound scattering cross section of the atom. A given material's energy and momentum exchange properties are defined by the thermal scattering laws stored in SCLM(α,β) tables. The thermal scattering laws are conveniently tabulated in terms of the dimensionless momentum transfer α and energy exchange β:
where A represents the ratio of the mass of the scattering nucleus M to the neutron mass mn.
Different theoretical models have been proposed to provide suitable analytical expressions of the thermal scattering laws. In this work, we are mainly interested in the analytic expressions derived in the framework of the incoherent and Gaussian approximations, which neglect interference terms in the inelastic scattering and average all possible orientations of the molecules using harmonic potentials [13]. The resulting expression is given by [14]:
where p stands for the number of phonons created or annihilated in the scattering event called “phonon expansion order”, λs is the temperature-dependent Debye-Waller coefficient and 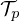 is the T-scrip function defined as follows:
is the T-scrip function defined as follows:
The zero-phonon term p=0 and the first term for p=1 are given by:
In Equation (11), the Debye-Waller coefficient can be calculated as follows:
in which ρ(β) represents the partial phonon density of states of the scattering atom in the material as already introduced in Figure 2. The zero-phonon term corresponds to elastic scattering because no phonon is created or annihilated, while the rest of the terms correspond to inelastic scattering.
2.3. Results for 238U in UO2
For nuclear applications, the Doppler broadening of neutron cross sections is routinely performed in the framework of the Free Gas Model (FGM) using algorithms such as SIGMA1 implemented in the NJOY processing code. Below the thermal cutoff energy, the Crystal Lattice Model of NJOY relies on 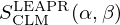 tables which can be calculated with its LEAPR module. The thermal cutoff energy is an arbitrary energy limit for changing from CLM to FGM where the two models provide nearly equivalent angle-integrated cross section values. Results obtained with these two approaches are compared in Figure 3 in the case of 238U in UO2.
tables which can be calculated with its LEAPR module. The thermal cutoff energy is an arbitrary energy limit for changing from CLM to FGM where the two models provide nearly equivalent angle-integrated cross section values. Results obtained with these two approaches are compared in Figure 3 in the case of 238U in UO2.
 |
Fig. 3. 238U neutron scattering cross sections calculated with the Free Gas and Crystal Lattice Models as shortly described in Sections 2.1 and 2.2. The top plot (a) compared the two models up to 100 eV, in which the dot blue line defines the thermal cutoff energy of 4 eV. The bottom plots (b), (c) and (d) highlight the results for the first three s-wave resonances of 238U obtained with the Free Gas and Crystal Lattice Models. The CLM calculation was performed by introducing in Equation (15) the phonon density of states shown in Figure 2. |
Below the thermal cutoff energy of about 4 eV, the large difference between the FGM and CLM calculations highlights the sizeable impact of the phonon density of states on the inelastic scattering contribution (Eq. (15)) and confirms that the Free Gas Model is not a valid approximation at low neutron energies for 238U in UO2. Similarly, above the thermal cutoff energy, the CLM formalism described in Section 2.2 is no longer valid because it was developed for constant cross sections. However, CLM calculations can be performed well above the thermal cutoff energy by replacing in Equation (3) the transfer function of the Free Gas Model with the one for the Crystal Lattice Model:
with
The obtained results in the vicinity of the first three s-wave resonances of 238U are shown in the bottom plots of Figure 3. The observed inconsistencies between the two models confirm that the extension of the CLM, as implemented in the LEAPR module of NJOY, over the entire neutron energy range is not so straightforward.
Figure 3 confirms that it is worth pursuing the development of a Doppler model to account for the dynamics of the molecule. However, obtaining a unified Doppler broadening formalism based on SCLM(α,β) was a long and tedious development work. The main development steps are summarized in the next sections. The first step consisted of studying how to introduce the recoil energy of the target nucleus in order to get resonances at their correct energy positions.
3. Combining CLM and recoil energy of the target nucleus
Preliminary tests shown in Figure 3 indicate that the gain in kinetic energy of the recoil nucleus has to be introduced in the Doppler broadening formalism.
By defining 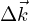 is the change of wave vector of any scattered neutron due to a collision with a single nucleus, the conservation of momentum between the nucleus momentum before (
is the change of wave vector of any scattered neutron due to a collision with a single nucleus, the conservation of momentum between the nucleus momentum before (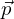 ) and after (
) and after (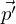 ) the collision gives:
) the collision gives:
The angle-dependent gain in kinetic energy of the recoil nucleus is then expressed as follows:
Given that for a fixed 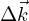 the average of
the average of 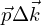 is zero, Equation (19) becomes:
is zero, Equation (19) becomes:
The same result was derived by Placzek in Ref. [15] using quantum-mechanical formalism. The average gain in energy over the scattering angles θ is then given by:
Two Doppler broadening formalisms were investigated by using either R(E,E′,μ) or R(E,E′). In the first one the zero Kelvin cross section is shifted by R(E,E′,μ):
In the second approach, 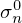 is shifted by the average energy gain R(E,E′) as follows:
is shifted by the average energy gain R(E,E′) as follows:
The Doppler broadened cross sections obtained via both methodologies are shown in Figure 4. The angle-dependent energy gain corrects the resonances’ energy position. However, their widths and amplitudes still need to be improved. Indeed, the observed differences between FGM and CLM are too large compared to the expected differences between these two models at room temperature. Despite these issues, the equations presented in this section provides a suitable theoretical framework to develop a valid Doppler broadening formalism. The expression (23) was useful to go in the direction of the α0 correction presented in Section 4 and Equation (22) together with the α0 correction lead to the α′ correction presented in Section 5.
 |
Fig. 4. Neutron elastic scattering cross sections in the vicinity of the first three s-wave resonances of 238U calculated with the Free Gas model approximation and the Crystal Lattice Models that encompass the angle-dependent recoil energy gain R(E,E′,μ) (Eq. (22)) and its average expression R(E,E′) (Eq. (23)). |
4. α0 correction relying on the average momentum transfer
According to results reported in Section 3, the next step is to determine for any given incident energy and target nucleus the momentum transfer distribution that provides a consistent angle-integrated cross section. The problem can be solved by introducing an average dimensionless momentum transfer α0. By introducing β (Eq. (10)) and replacing α by α0 in the zero Kelvin cross section 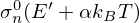 of Equations (22), (23) can be rewritten as follows:
of Equations (22), (23) can be rewritten as follows:
In this case, α0 can be calculated by a weighted mean value over all the possible α values to account for the different momentum transfer possibilities. The weighting function was the transfer function defined in Equation (17) which encompasses the molecular dynamics and scattering process information:
Figure 5 shows the neutron scattering cross section and the average dimensionless momentum transfer calculated with Equations (24) and (25) at 300 and 1474 K up to 100 eV for 238U in UO2. The comparison of these two observables confirms that the decrease of the inelastic scattering contribution below the thermal cutoff energy is strongly correlated to the energy-dependent behavior of α0. Above the thermal cutoff energy, the α0 values become equivalent to the asymptotic form:
which represents the dimensionless momentum transfer when a capture reaction occurs. This property of α0 is a useful illustration of the crystal lattice effects involved in the resonance and thermal energy ranges.
 |
Fig. 5. Neutron scattering cross sections calculated at 300 (a) and 1474 K (b) with the Free Gas Model and the Crystal Lattice Model based on the α0 correction. The α0 correction and its asymptotic form αcap are compared in the bottom plots (c) and (d) for the two temperatures. |
Results obtained in the resolved resonance range of 238U with Equation (24) are shown in Figure 6 for the two temperatures investigated in this work. At high temperatures, where the crystal lattice effects become negligible, the Crystal Lattice Model with the α0 correction is fully compatible with the Free Gas Model. At room temperature, the α0 correction significantly improves the Doppler broadening of the three first s-wave resonances of 238U compared to results shown in Figure 4. These encouraging results lead us to compare our Doppler broadening model with the Crystal Lattice Model implemented in the resonance analysis code SAMMY [7].
 |
Fig. 6. Neutron elastic scattering cross sections in the vicinity of the three first s-wave resonances of 238U calculated at 300 and 1474 K with the Free Gas model (black curves) and the Crystal Lattice Model based on the α0 correction (green curves). |
From the theoretical point of view, the asymptotic form of the α0 model, illustrated by αcap in Figure 8, is equivalent to the SAMMY approach in the case of an angle-integrated cross section. The theory was developed by Naberejnev in Ref. [2] and introduced successively in the REFIT [6], SAMMY [7] and CONRAD [8] codes. The difference between the model proposed by Naberejnev and the present one lies only in the mathematical way the models are written, given that SAMMY model only considers the asymptotic form of the α0 model. This asymptotic form also justifies why α0 and SAMMY models can be applied either for elastic scattering or radiative capture cross sections. The validity of the SAMMY model was verified with experimental 238U transmission measured at the JRC-Geel facility [16], making results from SAMMY useful for testing any CLM models. Figure 7 highlights the excellent agreement achieved between our model and SAMMY results confirming that the asymptotic form of α0 (Eq. (26)) is a good approximation to account for temperature-dependent crystal lattice effects in the resolved resonance range.
 |
Fig. 7. Results already shown in Figure 6 for T=300 K are compared with the neutron scattering cross sections calculated with the Crystal Lattice Model of the SAMMY code [7]. The CLM calculations were performed using the same partial phonon density of states shown in Figure 2. |
Results obtained in the thermal energy range with the α0 correction are shown in Figure 8. The comparison with the inelastic scattering contribution calculated with the Crystal Lattice Model of the NJOY processing code demonstrates that the use of α0 in Equation (24) is no longer valid below the thermal cutoff energy. To go further in the quantification of the missing inelastic scattering contribution, the 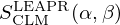 tables calculated with the LEAPR module of NJOY can be used to calculate the average momentum transfer
tables calculated with the LEAPR module of NJOY can be used to calculate the average momentum transfer 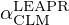 as follows:
as follows:
 |
Fig. 8. The plots (a, c) and the plots (b, d) represent the scattering cross sections and the average momentum transfer below the thermal cutoff energy as already shown in Figure 5. Plots (a, c) compare the previous results with the inelastic neutron scattering cross section calculated with the NJOY code using |
From the comparison of α0 and 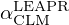 reported in Figure 8, the main difference comes from the change of the derivative with the energy increase. This change is more pronounced in the case of the α0 correction, while it can be approximated by two times the asymptotic form α0 (≃2αcap) in the case of the NJOY results.
reported in Figure 8, the main difference comes from the change of the derivative with the energy increase. This change is more pronounced in the case of the α0 correction, while it can be approximated by two times the asymptotic form α0 (≃2αcap) in the case of the NJOY results.
From the results reported in this section, we learn that the α0 approach can provide correct Doppler broadened cross sections in the resonance range, in which its asymptotic form αcap plays a crucial role. However, this approach underestimates the inelastic scattering contribution in the thermal energy range. Therefore, to improve the Doppler model in the thermal energy range without deteriorating the behavior above the thermal cutoff energy, attention should be paid to the derivative change of the average dimensionless momentum transfer with the energy increase.
5. α′ correction relying on the use of the zero phonon term
This section presents a unified Doppler broadening model for 238U in UO2 valid below and above the thermal cutoff energy based on two constraints. In the resonance range, the asymptotic form of the α0 correction has to be used, and in the thermal energy range, the inelastic contribution has to be described with the Van Hove original formalism (Eq. (17)). According to these constraints, Equation (22) can be modified as follows:
in which the α′ correction is defined as:
The dimensionless momentum transfer α′ is introduced in this Doppler broadening formalism to correct the angle-integrated cross section of the Van Hove formalism (Eq. (17)). The separation of the 2 contributions and multiplication with the asymptotic value αcap ensures that the two constraints defined above are fulfilled in their respective energy ranges. The temperature ratio between the effective temperature (Eq. (6)) and the nominal temperature is added to explain better the low-temperature range.
Figure 9 compares the neutron scattering cross sections calculated at 300 and 1474 K with the Free Gas Model, the NJOY code using 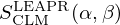 tables generated with its LEAPR module and the Crystal Lattice Model based on the α′ correction. The curves associated with NJOY and α′ correction are difficult to distinguish because they are on top of each other. This result confirms that Equation (28) allows to reproduce the Crystal Lattice Model of NJOY below the thermal cutoff energy. The smooth and continuous connection between the thermal and resonance ranges are illustrated in Figure 10. The Doppler broadened cross sections calculated in the vicinity of the first three s-wave resonances of 238U with the α0 and α′ corrections are indistinguishable, making the formalism fully compatible with the SAMMY results shown in Figure 7.
tables generated with its LEAPR module and the Crystal Lattice Model based on the α′ correction. The curves associated with NJOY and α′ correction are difficult to distinguish because they are on top of each other. This result confirms that Equation (28) allows to reproduce the Crystal Lattice Model of NJOY below the thermal cutoff energy. The smooth and continuous connection between the thermal and resonance ranges are illustrated in Figure 10. The Doppler broadened cross sections calculated in the vicinity of the first three s-wave resonances of 238U with the α0 and α′ corrections are indistinguishable, making the formalism fully compatible with the SAMMY results shown in Figure 7.
 |
Fig. 9. Neutron scattering cross sections of 238U in UO2 calculated at 300 (a) and 1474 K (b) with the Free Gas Model (black curve), the NJOY code using |
 |
Fig. 10. Neutron elastic scattering cross sections in the vicinity of the three first s-wave resonances of 238U calculated at 300 and 1474 K with the Free Gas Model (black curve), the Crystal Lattice Model based on the α0 correction (green curve) and the Crystal Lattice Models based on the α′ correction (blue curve). The green and blue curves are on top of each other. |
Equation (28) provides consistent results for 238U because the first resonances are above the thermal cutoff energy. This property ensures a smooth connection between the thermal and resonance ranges. The validity of the α′ correction for nuclei having resonances below the thermal cutoff energy is investigated with 240Pu in PuO2 and 237Np in NpO2. Figure 11 displays the neutron scattering cross sections calculated with the various models presented in this work for both materials. The Crystal Lattice Model based on the α′ correction follows the expected trends in the thermal energy range and in the resonance range well above 3 eV. At room temperature, the crystal lattice effects are still important between approximately 0.1 and 3 eV, inducing sizeable differences with the Free Gas Model. Such differences can be well observed in Figures 12 and 13 for 240Pu and 237Np, respectively.
 |
Fig. 11. Neutron scattering cross sections of 240Pu in PuO2 (a, b) and 237Np in NpO2 (c, d) calculated at 300 and 1474 K with the various Doppler broadening models investigated in this work. |
 |
Fig. 12. Neutron elastic scattering cross sections in the vicinity of the three first s-wave resonances of 240Pu calculated at 300 and 1474 K with the Free Gas Model (black curve), the Crystal Lattice Model based on the α0 correction (green curve) and the Crystal Lattice Models based on the α′ correction (blue curve). |
 |
Fig. 13. Neutron elastic scattering cross sections of 237Np calculated up to 20 eV with the Doppler broadening models shown in Figure 11. |
The theoretical results obtained on the Doppler broadening of the first resonances of 240Pu and 237Np using a Crystal Lattice Model valid over a broad energy range were never reported in the literature. Unfortunately, experimental evidence of the temperature effects calculated between 0.1 and 3 eV does not exist. Indeed, transmission measurements on 240Pu and 237Np available in the literature are dominated by the capture process, and elastic scattering measurements covering the low neutron energy resonances of these two isotopes were never performed. The analysis of older scattering experiments on 233U and 241Pu carried out by Sauter et al. [17] from 1 to 30 eV could be of interest for this work. In parallel, a review of the existing elastic data on non-fissile materials is underway [18]. An alternative option would be to investigate the neutron scattering capabilities of the VESUVIO detector located at the spallation neutron source ISIS (UK) [19] in order to design a suitable experimental Doppler program.
6. Conclusions
A unified Doppler model able to account for temperature-dependent crystal lattice effects on the neutron elastic scattering cross sections has never been reported in the literature. The present work demonstrates that a simple formula in association with SCLM(α,β) thermal scattering laws can be used to solve this issue. The paper highlights the importance of the recoil energy and average momentum transfer which are two important quantities to establish the α0 and α′ models discussed in this work. Beyond the performances of the α′ model, this work evidences that the Doppler broadening of the neutron resonances below the thermal cutoff energy is not correctly taken into account by the formalisms available in the processing codes. This key result must be confirmed experimentally using data available in the literature or with new experimental programs that could be carried out in facilities such as SNS (USA), ILL (France) or ISIS (UK). The next theoretical step will be to use the results obtained in this work to explore the anisotropy of the elastic scattering reactions as a function of the scattering angle.
Funding
This work is carried out in the framework of the SINET projects funded by the CEA.
Conflicts of interest
The authors declare that they have no competing interests to report.
Data availability statement
The data that support the findings of this study are available on request from the corresponding author.
Author contribution statement
A. Bengoecha: methodology, software, writing, review, editing. G. Noguere, D. Bernard: methodology, review, editing.
References
- R.E. MacFarlane, D.W. Muir, Nucl. Data Sheets 111, 2739 (2010) [Google Scholar]
- D.G. Naberejnev et al., Ann. Nucl. Energy 28, 1 (2001) [Google Scholar]
- A. Courcelle, J. Rowlands, Approximate Model of Neutron Resonant Scattering in a Crystal, arXiv:0709.2767 (2007) [Google Scholar]
- A.J. Villanueva, J.R. Granada, Ann. Nucl. Energy 38, 1389 (2011) [Google Scholar]
- N.C. Fleming, A.I. Hawari, J. Nucl. Eng. 2, 124 (2021) [Google Scholar]
- M.C. Moxon, T.C. Ware, C.J. Dean, REFIT-2009: A least-square program for resonance analysis of neutron transmission, capture, fission and scattering data, users guide for REFIT-2009-10 (2010) [Google Scholar]
- N.M. Larson, Updated User's Guide for Sammy: Multilevel R-Matrix Fits to Neutron Data Using Bayes’ Equations, ORNL Technical. https://doi.org/10.2172/941054, 2008 [Google Scholar]
- C. De Saint Jean et al., EPJ Nucl. Sci. Technol. 7, 10 (2021) [Google Scholar]
- A.W. Solbrig, Am. J. Phys. 29, 257 (1961) [Google Scholar]
- W.E. Lamb, Phys. Rev. 2, 190 (1939) [Google Scholar]
- L. Van Hove, Phys. Rev. 1, 249 (1954) [Google Scholar]
- G. Noguere et al., Phys. Rev. B 102, 134312 (2020) [CrossRef] [Google Scholar]
- A.W. Solbrig, Am. J. Phys. 28, 680 (1960) [Google Scholar]
- G.L. Squires, Introduction to the Theory of Thermal Neutron Scattering (Cambridge University Press, 2012) [Google Scholar]
- G. Placzek, Phys. Rev. 86, 377 (1952) [Google Scholar]
- A. Courcelle et al., AIP Conf. Proc. 769, 394 (2005) [Google Scholar]
- G.D. Sauter, C.D. Bowman, Phys. Rev. 174, 1413 (1968) [Google Scholar]
- N. Otuka et al., Nucl. Data Sheets 120, 272 (2014) [CrossRef] [Google Scholar]
- J. Mayers et al., Physica B Condens. Matter 350, E659 (2004) [Google Scholar]
Cite this article as: A. Bengoechea Fernández, G. Noguerea, and D. Bernarda. Doppler broadening of neutron elastic scattering cross section using SCLM(α,β) thermal scattering laws, EPJ Nuclear Sci. Technol. 11, 34 (2025). https://doi.org/10.1051/epjn/2025032
All Figures
 |
Fig. 1. 238U in UO2 (a) and 240Pu in PuO2 (b) neutron scattering cross sections calculated at 294 K by using the Free Gas Model (FGM) and Crystal Lattice Model (CLM) of the NJOY processing code [1]. The thermal cutoff energies are equal to 4 eV and 0.26 eV, respectively. The SIGMA1 algorithm is used for FGM, and the LEAPR module is used for CLM. |
| In the text | |
 |
Fig. 2. Partial phonon densities of states of 238U in UO2 at 300 and 1474 K deduced from inelastic neutron scattering experiments carried out at the Institute Laue-Langevin [12]. |
| In the text | |
 |
Fig. 3. 238U neutron scattering cross sections calculated with the Free Gas and Crystal Lattice Models as shortly described in Sections 2.1 and 2.2. The top plot (a) compared the two models up to 100 eV, in which the dot blue line defines the thermal cutoff energy of 4 eV. The bottom plots (b), (c) and (d) highlight the results for the first three s-wave resonances of 238U obtained with the Free Gas and Crystal Lattice Models. The CLM calculation was performed by introducing in Equation (15) the phonon density of states shown in Figure 2. |
| In the text | |
 |
Fig. 4. Neutron elastic scattering cross sections in the vicinity of the first three s-wave resonances of 238U calculated with the Free Gas model approximation and the Crystal Lattice Models that encompass the angle-dependent recoil energy gain R(E,E′,μ) (Eq. (22)) and its average expression R(E,E′) (Eq. (23)). |
| In the text | |
 |
Fig. 5. Neutron scattering cross sections calculated at 300 (a) and 1474 K (b) with the Free Gas Model and the Crystal Lattice Model based on the α0 correction. The α0 correction and its asymptotic form αcap are compared in the bottom plots (c) and (d) for the two temperatures. |
| In the text | |
 |
Fig. 6. Neutron elastic scattering cross sections in the vicinity of the three first s-wave resonances of 238U calculated at 300 and 1474 K with the Free Gas model (black curves) and the Crystal Lattice Model based on the α0 correction (green curves). |
| In the text | |
 |
Fig. 7. Results already shown in Figure 6 for T=300 K are compared with the neutron scattering cross sections calculated with the Crystal Lattice Model of the SAMMY code [7]. The CLM calculations were performed using the same partial phonon density of states shown in Figure 2. |
| In the text | |
 |
Fig. 8. The plots (a, c) and the plots (b, d) represent the scattering cross sections and the average momentum transfer below the thermal cutoff energy as already shown in Figure 5. Plots (a, c) compare the previous results with the inelastic neutron scattering cross section calculated with the NJOY code using |
| In the text | |
 |
Fig. 9. Neutron scattering cross sections of 238U in UO2 calculated at 300 (a) and 1474 K (b) with the Free Gas Model (black curve), the NJOY code using |
| In the text | |
 |
Fig. 10. Neutron elastic scattering cross sections in the vicinity of the three first s-wave resonances of 238U calculated at 300 and 1474 K with the Free Gas Model (black curve), the Crystal Lattice Model based on the α0 correction (green curve) and the Crystal Lattice Models based on the α′ correction (blue curve). The green and blue curves are on top of each other. |
| In the text | |
 |
Fig. 11. Neutron scattering cross sections of 240Pu in PuO2 (a, b) and 237Np in NpO2 (c, d) calculated at 300 and 1474 K with the various Doppler broadening models investigated in this work. |
| In the text | |
 |
Fig. 12. Neutron elastic scattering cross sections in the vicinity of the three first s-wave resonances of 240Pu calculated at 300 and 1474 K with the Free Gas Model (black curve), the Crystal Lattice Model based on the α0 correction (green curve) and the Crystal Lattice Models based on the α′ correction (blue curve). |
| In the text | |
 |
Fig. 13. Neutron elastic scattering cross sections of 237Np calculated up to 20 eV with the Doppler broadening models shown in Figure 11. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



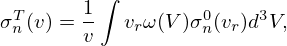
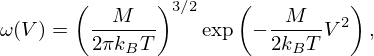
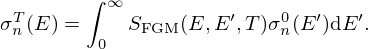
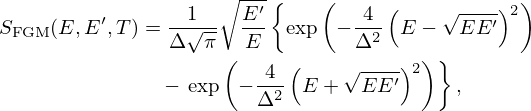
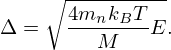
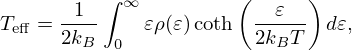
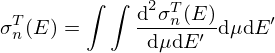
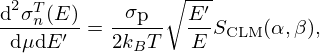
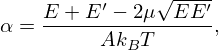
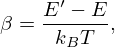
![$$ S_{\mathrm {CLM}}(\alpha , \beta ) = e^{-\alpha \lambda _s}\sum ^\infty _{p=0}\frac {1}{p!}[\alpha \lambda _s]^p{\cal {{T}}}_p(\beta ), $$](/articles/epjn/full_html/2025/01/epjn20250005/epjn20250005-eq14.gif)
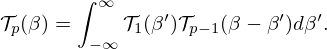
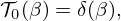
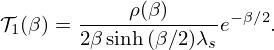
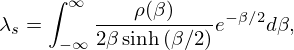
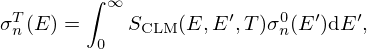
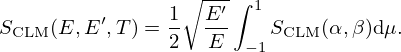
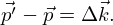
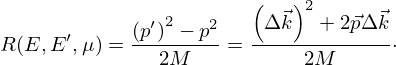
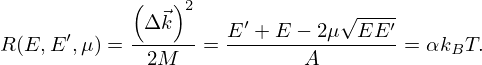
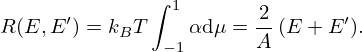
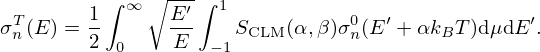
![$$ \sigma ^T_n(E) = \int ^\infty _0 S_{\mathrm {CLM}}(E, E^\prime , T)\sigma ^0_n\left (E^\prime + \frac {2}{A}\left [E + E^\prime \right ]\right ) \mbox {d}E^\prime . $$](/articles/epjn/full_html/2025/01/epjn20250005/epjn20250005-eq34.gif)