| Issue |
EPJ Nuclear Sci. Technol.
Volume 10, 2024
|
|
|---|---|---|
| Article Number | 1 | |
| Number of page(s) | 10 | |
| DOI | https://doi.org/10.1051/epjn/2024002 | |
| Published online | 19 March 2024 | |
https://doi.org/10.1051/epjn/2024002
Regular Article
Rheological investigation of bitumen, used for radioactive waste conditioning, with ultrasonic waves
1
IES, University of Montpellier, CNRS, Montpellier, France
2
Institut de Radioprotection et de Sûreté Nucléaire (IRSN), PSE-ENV/SPDR/USDR, 92260 Fontenay-aux-Roses, France
* e-mail: didier.laux@umontpellier.fr
Received:
11
December
2023
Received in final form:
24
January
2024
Accepted:
26
January
2024
Published online: 19 March 2024
In the context of bituminized radioactive waste storage and disposal, nucleation monitoring at room temperature and radiolysis bubbles migration at elevated temperature is crucial particularly in fire scenarios where bubble may impact thermal properties. Traditional methods are limited by the opacity of bitumen. To gain a deeper insight into bitumen rheology and ultrasonic wave propagation, we conducted a pilot study using ultrasonic testing cells spanning temperatures from 10°C to 60°C. Ultrasonic velocities and attenuations were measured at around 500 kHz in a 70/100 grade bitumen. Rheological information was deduced with the Time-Temperature Superposition principle and a behaviour model was proposed to describe bitumen across a wide frequency range. Notably, our study reveals a transition point around 50°C to 60°C, where bitumen’s liquid behaviour becomes dominant. The shear-thinning characteristics gradually give way to a more Newtonian response. Using the proposed model, ultrasonic attenuation and viscosity were estimated at 110°C. Acceptable ultrasonic frequencies for monitoring the nucleation and migration of radiolysis bubbles are discussed for future investigations. These findings have significant implications for safety measures and a deeper understanding of bitumen response within the realm of radioactive waste management.
© D. Laux et al., Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In the nuclear industry, the bituminization of radioactive waste is a conditioning process used to immobilize and contain radioactive waste into a bitumen matrix. This process has been widely used throughout the world and was implemented as early as the 1950s [1–3]. In France, 70/100 distilled bitumen is commonly used, and the repository of such waste encompasses over than 70 000 waste packages [4] classified as long-lived low- and intermediate-level waste. Hardness and viscoelasticity stand as important rheological characteristics of Bituminized Radioactive Waste (BWRs) governing their handling, transport, and storage [1]. Nonetheless, the influence of ionizing radiation-induced radiolysis leads to notable alterations in these material properties [4, 5]. Notably, the radiolysis-induced changes bear significant implications for the assessment of fire and explosion risks associated with BRWs, a principal concern in both the storage and operational disposal of these packages [6, 7].
Radiolysis of bitumen also results in the generation of hydrogen, light hydrocarbons, and other gases (NO, NO2, CH3NH2, etc.) [8, 9], often manifested in the form of gas bubbles, which can significantly elevate the fire and explosion risk when released. Although the quantities of radiolysis gases generated are typically modest, they remain a monitored parameter, holding substantial influence over nuclear safety, particularly concerning fire risks [6, 7]. Given this context, it becomes imperative to comprehensively investigate the repercussions of radiolysis on the bitumen matrix to effectively model its behaviour in fire scenarios [6].
Extensive research has been conducted on bitumen viscoelastic properties, bubbles growth and rising in bitumen drums, and on the effect of γ irradiation on the bitumen rheology [10–15]. In the context of assessing opaque materials, ultrasonic approaches emerge as particularly relevant. The detection of ultrasonic bubbles has been widely discussed in the scientific literature [16–21], catering to the needs of diverse industries. These methods are used particularly in high-speed fluidics (cavitation problems), in agronomy for pasta development [16] or emulsion control [17], as well as in the polymer industry (foams in the broadest sense). The problem of bubbles nucleating on impurities, rising in a liquid, and affecting acoustic waves is often referred to as the “Hot Chocolate Effect”, in reference to a 1982 experiment [18–20]. In the nuclear industry, ultrasonic propagation in opaque liquids has been used to study sodium [21]. In the case of bitumen, ultrasonic studies [22–24] have been carried out to determine the complex elastic moduli to establish behaviour laws or viscosity dependence versus temperature or shear rate. For example, a comprehensive study [22] was carried out on 35/50 bitumen.
Surprisingly, the literature review has failed to reveal any ultrasonic studies dedicated to the monitoring of a bubble population within a bitumen matrix subjected to both irradiation and heating up to several hundred degrees. This glaring gap underscores the innovative nature of this investigation. In fact, ultrasonic studies on bitumen have mainly focused on a temperature range not exceeding 40°C [22]. Nevertheless, it is noteworthy that more recent literature has introduced a transmission method for “extra-heavy oil” reaching temperatures as high as 140°C [24].
With these considerations in mind, this study aims to explore the potential of acoustic methods for monitoring these phenomena at different temperatures, from room temperature up to 110°C. Additionally, measurements of ultrasonic velocities and attenuation over a temperature range from 10 to 60°C were used to establish master curves for ultrasonic attenuation and longitudinal viscosity, thanks to the application of the Time-Temperature Superposition principle (TTS). Ultimately, the overarching goal of this research is to evaluate the capabilities of acoustic methods in monitoring the formation and migration of radiolysis bubbles in the context of radioactive waste storage and disposal. This entails the application of 500 kHz ultrasonic waves to 70/100 bitumen, encompassing temperatures ranging from ambient level to 110°C.
In the first part of this paper the experimental protocol using a transmission approach will be described for bitumen study in experimental cells and for a PMMA calibration sample. Then, results obtained in terms of attenuation and velocity versus temperature (in the range 10 − 60°C and versus frequency will be presented and discussed regarding data for 35/50 bitumen presented in [22]. These measurements will be used for the rheological behaviour of bitumen estimation and extrapolation to temperatures in the range 70 − 110°C. This extrapolation will be discussed and compared to bibliographic data reported for other bitumen grades. At last, regarding all these elements, acceptable ultrasonic frequencies for monitoring the nucleation and migration of radiolysis bubbles will be discussed for future investigations.
2. Material and methods
2.1. PMMA sample
In order to validate our experimental contact methods (see part 2.3.2), tests were performed on PMMA samples with a 50 mm diameter and lengths of 7.84, 16.31, 24.70 and 49.85 mm. These samples were cut in a 2 m bar purchased from Novaplest (90400 Danjoutin, France). This PMMA had been previously investigated in reference [25] using a non-contact immersion ultrasonic method and its ultrasonic velocity and attenuation dependence versus frequency and temperature are perfectly known. At room temperature (20°C), the ultrasonic velocity is 2750 m.s−1 and attenuation can be calculated using the following relationship:
The previous relationship is in very good agreement with literature data and for instance with Carlson et al. works [26]. For a temperature of 20°C and a frequency of 5 MHz they found 60.84 Np.m−1. Relationship (1) gives 60 Np.m−1. As explained in [25], in the literature several authors have proposed a linear law between attenuation and frequency. Generally, these laws are given over a few MHz. Relationship (1) was established from 20 kHz to 12 MHz but over a few MHz its global trend is not far from linearity. In [25] the non-linearity observed for low frequencies was interpreted thanks to the possible existence of a γ relaxation regarding activation energy calculated.
2.2. 3D printing of bitumen cells
Test cells with three different thicknesses (see Tab. 1) were designed using 3D printing as illustrated in Figure 1. Cell No.3 features dimensions suitable for future studies focused on bubble generation using γ irradiation. It was estimated that this cell had a sufficient volume to investigate bubble clouds with diameters ranging from a few micrometres to a few millimetres. For subsequent irradiation experiments, a metal version of this cell will be made.
Bitumen thickness for the 3 cells.
 |
Fig. 1. Bitumen cells with 3 different thickness designed with 3D printing. |
The 3D printing of cells for bitumen research was carried out using Fused Deposition Modelling (FDM) technology with a single extruder system. The available print volume was 210 × 210 × 250 mm, and a 1.75 mm diameter thermoplastic filament, specifically PLA (a polyester-type polymer known for its suitability in FDM printing), was used. The filament for Cell No. 1 and 2 was yellow, while for Cell No. 3, it was white. The printing process featured a precision of 50 μm for all axes. The printing process involved a 0.4 mm diameter nozzle at a temperature of 245°C. A glass print bed was used with PrintaFix adhesive for material adhesion. The printing environment, although uncontrolled, maintained an ambient temperature of 40°C to 60°C. The print speed was set at 4200 mm.min−1 with a layer height of 250 μm. The smallest cell required approximately 4 h for the printing process. Annealing is then carried out in the sand for more than 24 h at 80°C. Subsequently, following 3D printing, 1 mm thick glass windows were incorporated.
2.3. Ultrasonic longitudinal spectroscopy
2.3.1. General method and working equations
When only one sample is available, the general principle is to compare the ultrasonic signal transmitted through a well-known standard material (usually water) with those transmitted through the analysed sample. However, when various thicknesses of the same sample can be obtained, the ultrasonic signals transmitted in the samples can be studied versus thickness in order to deduce the ultrasonic velocity and attenuation. Let dG and dB be the thicknesses of the glass plates (used for experimental cell conception) and bitumen respectively. So, if vB and vG represent the ultrasonic velocities in bitumen and glass, then, the propagation time tprop of an ultrasonic signal through a given sample is written:
As the bitumen cells were all made with the same glass plates, it is not necessary to know vG. If the arrival time of the ultrasonic signal is plotted as a function of bitumen or cell thickness, then the curve obtained is a straight line with slope equal to  . So, the ultrasonic velocity vB is deduced. Furthermore, during its propagation, the ultrasonic waves are attenuated in glass and bitumen. Consequently, the amplitude A of an ultrasonic signal can be written as:
. So, the ultrasonic velocity vB is deduced. Furthermore, during its propagation, the ultrasonic waves are attenuated in glass and bitumen. Consequently, the amplitude A of an ultrasonic signal can be written as:
This expression αBW represents the mean value of bitumen spectral attenuation αB(f) (defined by relationship (4)) calculated on the sensor’s bandwidth, typically here from 250 kHz to 650 kHz. Φ is a constant which represents both ultrasonic attenuation in glass and insertion losses caused by acoustical impedance changes between ultrasonic transducers (See Sect. 2.3.2), glass and bitumen. So, if ln(A) is plotted versus dB, the graph obtained is a straight line with a slope equal to −αBW. So, αBW is straightforwardly deduced. For viscous materials such as bitumen, even if αBW is a first global interesting parameter, the attenuation versus frequency αB(f) is more relevant because it can be linked to rheological parameters such as viscosity. By analogy with (3), the modulus |S(f)| of the Fourier’s transform of the ultrasonic signal attenuated during its propagation can be writtenas:
 |
Fig. 2. Experimental bench (cell + transducers) in the thermoregulated chamber. |
So, for a chosen frequency f, the plot of |S(f)| versus dB leads to αB(f). The repetition of the procedure for various frequencies leads to αB(f) estimation of the sensor’s bandwidth. With the knowledge of spectral attenuation αB(f) in Np.m−1 ultrasonic velocity in bitumen vB in m.s−1 and mass density ρB in kg.m−3, it is possible to define the longitudinal viscosity ηL in Pa.s as follows [27], where f is the frequency expressed in Hz:
Remark:
In order to interpret this specific viscosity, it can be recalled [25] that for longitudinal waves, their propagation is linked to the complex longitudinal modulus L*, which is a combination of the complex shear G* and bulk modulus K*:  . In terms of imaginary parts, the previous relation can be written as:
. In terms of imaginary parts, the previous relation can be written as:  . By analogy with the definition of shear viscosity ηs, namely
. By analogy with the definition of shear viscosity ηs, namely  , the longitudinal viscosity is then expressed as a combination of shear and compressional (bulk) viscosity ηB as follows :
, the longitudinal viscosity is then expressed as a combination of shear and compressional (bulk) viscosity ηB as follows :  . This subject has been widely investigated in literature for simple liquids [27–29]. For heavy oils and bitumen one can refer to Rabbani’s work [24]. For Newtonian liquids it can be simply addressed because ηL is proportional to ηs (Trouton’s law) This point will be evocated further at the end of this communication
. This subject has been widely investigated in literature for simple liquids [27–29]. For heavy oils and bitumen one can refer to Rabbani’s work [24]. For Newtonian liquids it can be simply addressed because ηL is proportional to ηs (Trouton’s law) This point will be evocated further at the end of this communication
2.3.2. Experimental bench and signal processing
For signal emission and reception, we mainly used a couple of 30 mm diameter (Olympus – V101 RM VISIOSCAN) transducers with a wide bandwidth ranging from 250 kHz to 650 kHz. These transducers were chosen because they are similar to those used in reference [22], in order to compare experimental results. With these commercial transducers, it was not possible to heat over 60°C, following manufacturer recommendations. Measurements at room temperature were also performed with a couple of 1 MHz Sonaxis transducers (CMP107 – Diameter: 1 cm) and with a couple of 2.25 MHz transducers (Olympus – V323 SM – Diameter: 0.6 cm). For the PMMA calibration sample, a couple of 5 MHz Olympus transducers (V310 SU – Diameter: 0.6 cm) were chosen to be sure that a pure longitudinal wave (and not an elongational one) is generated in the PMMA rod. Lower frequencies and sensors with higher diameters do not guarantee this condition. For each experiment, one transducer acted as an ultrasound emitter, the other as receiver. Liquid honey was used as a coupling agent to ensure good transmission of the ultrasonic waves between transducers and the cell’s glass plates. Cells and sensors were mounted on an adjustable bench with two clamping screws to maximize (sensor/cell) contact and avoid signal losses. A thermometer was placed close to this adjustable bench to monitor temperature during measurements. The bench was placed in a BINDER thermoregulated chamber ranging from −10°C to 100°C. A photograph of this experimental bench is displayed in Figure 2. These sensors were connected to a JSR Ultrasonics DPR300 pulser/receiver generator and the acoustic signals were then visualized using a LeCroy WaveJet 334 oscilloscope. The acquisition of the acoustic signal was carried out with in-house LabView software. The ultrasonic signal was acquired from the oscilloscope to the computer using a National Instruments (USB/GPIB HS+) transfer cable. After signal acquisition, the envelope of the signal was calculated with the help of a Hilbert transform. Its maximum value and temporal position were plotted versus cell thickness in order to calculate αBW and vB. We also calculated S(f) with a Fast Fourier’s transform algorithm and deduced α(f) over the sensor bandwidth. All signal processing was made with in-house Python software written in the Spyderinterface.
Remark:
In order to consider diffraction effects due to the finite size of the transducers, the procedure described in [30] was used. The calculation, involving Bessel functions is not detailed in this communication. Results showed that these diffraction losses decrease with increasing frequency. For instance, they can reach 4 Np.m−1 at 250 kHz and are reduced to 1 Np.m−1 for an operating frequency of 1 MHz. One has to bear in mind that analytical relationships used and presented in [30] constitute a first-order approximation and so it is very important to check that diffraction losses are inferior to attenuations measured. Regarding values measured in paragraph 3.2.1 this condition is totally respected. Calculations also showed that diffraction phenomena have a negligible effect on the velocities measured. So, for velocities estimation they were not taken into account.
2.3.3. Temperature control and stabilisation time
In order to estimate the time taken to heat or cool the cells, we used both a 1D model (oriented on x axis) considering a bitumen layer of thickness e and the propagation time of the ultrasonic signals through the cell. To is the initial temperature of bitumen and for t = 0 a temperature T1 is imposed in positions x = 0 and x = e. It is possible to calculate the temperature for  versus time [31]. If this temperature does not evolve at all, this means that the equilibrium has been reached. It can be shown that equilibrium is reached for a time tEQ after heating or cooling given by [31]:
versus time [31]. If this temperature does not evolve at all, this means that the equilibrium has been reached. It can be shown that equilibrium is reached for a time tEQ after heating or cooling given by [31]:
In relationship (6), λ is the thermal conductivity in W.kg−1.K−1, ρ is the mass density in kg.m−3, Cp the heat capacity in J.K−1.kg−1 and κ the thermal diffusivity expressed in m2.s−1. In can also be considered that for a time tSTAB ∼ 0.4 tEQ, the temperature reaches more than 99% of T1 [31]. Consequently tSTAB can be considered to be the time when a quasiperfect equilibrium is reached. In order to compare this estimation to experimental results we used ultrasonic signal as follows. As ultrasonic velocity is a function of temperature (See Sect. 3.2.1) the arrival time of the ultrasonic signal transmitted through the sample is influenced by temperature. Furthermore, as the ultrasonic velocity is a linear function of temperature (See Sect. 3.2.1), straightforward calculations demonstrate that the arrival time can be considered as proportional to temperature. The temporal position tenvelope, of the ultrasonic signal envelope maximum was measured versus time during the heating of bitumen from T0 to T1.
In practice the cell (temperature T0) was put in the BINDER thermoregulated chamber in which the temperature was already stabilized at T1. The curve (tenvelope versus time) was then normalized between T0 and T1. An example is presented in Figure 3 for cell No.3, T0 = 21°C and T1 = 26°C.
 |
Fig. 3. Mean cell No.3 temperature as estimated with ultrasounds. |
Regarding this figure the stabilisation of temperature through bitumen was reached at around 5000–6000 s. This range is in good agreement with thermal values classically found in the literature [22]: Cp ∼ 2000 J.K−1.kg−1, ρ ∼ 1030 kg.m−3, λ ∼ 0.20 W.kg−1.K−1 which led to tSTAB ∼ 5300 s. For this cell we choose a stabilisation time of 5400 s = 1.5 h in order to use multiple hours. The same work performed on the other bitumen cells led to tSTAB = 1800 s and tSTAB = 3600 s for cells No. 1 and No. 2 respectively.
Remark: instead of the calculation proposed in [31] it would also have been possible to adjust the evolution of temperature versus time with the following relationship:
This relationship is a very first approximation of heating or cooling phenomena assuming that no gradient exists in the material. It is sometimes called the Newton cooling. In this expression, τ is the time constant of the phenomenon and is related to heat transfers on boundaries, material mass, contact surface, and heat capacity. It can be admitted that the equilibrium is quite reached for a time between 3τ and 4τ. The adjustment is presented in Figure 3 and led to τ ∼ 1600 s, 3τ = 4800 s and 4τ = 6400 s. These values are in agreement with the more complex evaluation from reference [31] previously presented.
2.4. Time-Temperature Superposition applied to ultrasonic data and viscosity
Time-Temperature Superposition (TTS), widely applied in shear rheology, is based on the principle that measurements at a high temperature correspond to measurements at a low frequency and vice versa [32, 33]. In our previous study dedicated to PMMA [25] investigation, the application of TTS directly on ultrasonic data has been discussed: attenuation was first measured for various temperatures and for various frequencies within the ultrasonic transducers’ bandwidth. Then, a reference temperature TREF was chosen, and a shifting factor aT was found so that (α.aT)at a temperature T overlaps for the frequency range (aT.f) with the attenuation measured at the chosen reference temperature. Mathematically, TTS applied to ultrasonic attenuation is written as [25]:
After the TTS application, the attenuation was obtained for the temperature TREF on an enlarger bandwidth. For instance, on PMMA in reference [25], measurements performed between 2 and 8 MHz and for temperatures ranging from 6 to 45°C led to results between 600 kHz and 10 MHz for a reference temperature of 20°C. With attenuation and relationship (5), longitudinal viscosity can be also deduced on a large bandwidth for a chosen reference temperature. But it is also possible to directly work on viscosity [13]. In this case, TTS is applied as follows:
Attenuation values measured and calculated on PMMA calibration sample.
At last, the values of aT can be adjusted with an Arrhenius law (10) in which R = 8.314 J.mol−1.K−1 is the constant of perfect gases, in order to calculate the activation energy Ea in J.mol−1 [32]:
3. Results
3.1. Validation of PMMA sample
Repeatability tests showed that the accuracy, with two standard deviations, was ±5 Np.m−1 for attenuation and ±30 m.s−1 for velocity. For the latter, we found 2749 m.s−1. Such a value is perfectly in line with those reported in [25]. In Table 2, the values of αPMMA(f) actually measured and calculated with relationship (1) clearly validate the contact method with 3 thicknesses and demonstrate that sensors repositioning to perform the measurements on different bitumen cells will not constitute a problem.
3.2. 70/100 bitumen
3.2.1. Ultrasonic attenuation and velocity
For 70/100 bitumen, the results in terms of attenuation αBW and velocity vB on the sensors bandwidth are displayed in Figures 4a and 4b. We also reported values given in [22], extracted with the free software “graphreader (http://www.graphreader.com)”. Ultrasonic velocity decreases from 2000 m.s−1 at 10°C to 1480 m.s−1 at 60°C. The following relationship (reported in Fig. 4a) can be proposed :
 |
Fig. 4. (a) Ultrasonic properties of bitumen 70/100 compared to 35/50 bitumen data (a) velocity vB (b) attenuation αBW. |
For a given temperature, the velocity measured in our 70/100 bitume is smaller than those obtained by Larcher [22] for his 35/50 bitume. Such an element is not surprising: our bitume is softer (more liquid).
For attenuation, our results are in line with the results given in litterature for the 35/50 bitumen up to 40°C. A decrease is observed above 40°C. Rabbani [24] also observed this attenuation peak which is attributed to microstructural changes and in particular to asphaltens mobility increase with temperature [10, 13]. These first results on sensor bandwidth showed that working with 500 kHz transducers is totally possible even for the 3.5 cm cell. With such a frequency the wavelength is around 3.6 mm at 20°C, 3 mm for 60°C and should reach 2 mm at 100°C using relationship (11). In order to work with smaller wavelengths to increase the special resolution for better bubble detection in the framework of future studies, the question of frequency increase must be addressed. So, TTS was applied for TRef = 20°C using attenuation measurements versus frequency between 250 and 650 kHz and temperatures ranging from 10 to 60°C, using the procedure described in Sections 2.3 and 2.4. The result is displayed in Figure 5 in the enlarged frequency range 10 kHz to 10 MHz. In this figure we also reported the value of attenuation estimated with the 1 MHz and 2.25 MHz transducers. Error bars for 2 MHz measurements are large because the signal was attenuated a lot rendering the experiment quite tricky. Experimentally, it can be considered that, when attenuation reaches ∼150 Np.m−1 measurements are difficult. Indeed, for a typical cell thickness of around 3.5 cm, the initial signal is divided by a factor 200. Working with a so small signal becomes difficult. Regarding these results, at room temperature, frequency should have been inferior to 2 MHz. This limitation will be discussed at the end of this communication.
 |
Fig. 5. Ultrasonic attenuation in 70/100 bitumen for T = 20°C, after TTS application on data measured with 500 kHz transducers and comparison with direct estimations, using 1 MHz and 2.25 MHz sensors. |
These measurements are totally in line with TTS results and constitute a proof of TTS validity. In Figure 6, ln(aT) versus (1/T − 1/TRef) is presented. It was not possible to obtain a correct linear adjustment on the whole temperature range. The linear behaviour was only established between 10°C and 50°C. As previously explained, this is certainly due to the behaviour evolution around 50°C, attributed to asphaltens mobility increase. So, we have reduced the range to 10 − 50°C. The linear adjustment (R2 = 0.997) leads to  . In reference [13], Mouazen et al. found higher values between 161 kJ.mol−1 and 175 kJ.mol−1, using classical rheology, and in literature [34], values between 117 kJ.mol−1 and 145 kJ.mol−1 are also reported for bitumen with various grades. Such a result is particularly interesting because we found the same order of magnitude of Ea with ultrasounds and with very different experimental methods on very different bandwidths.
. In reference [13], Mouazen et al. found higher values between 161 kJ.mol−1 and 175 kJ.mol−1, using classical rheology, and in literature [34], values between 117 kJ.mol−1 and 145 kJ.mol−1 are also reported for bitumen with various grades. Such a result is particularly interesting because we found the same order of magnitude of Ea with ultrasounds and with very different experimental methods on very different bandwidths.
 |
Fig. 6. ln(aT) versus (1/T − 1/TRef) for TRef = 20°C and linear adjustment for activation energy determination. |
3.2.2. Viscosity
To further investigate the rheological behaviour of bitumen and to deduce a behaviour law for extrapolation in the range 50 − 110°C, we first estimated the longitudinal viscosity as a function of temperature and frequency (See Fig. 7). As temperature increases, the shear thinning behaviour is less important and it would appear to show that bitumen slowly tends to a Newtonian behaviour. Up to 55°C, the data could be adjusted with a power law ηL ∼ f−1. In other words, considering relationship (5) this means that attenuation follows a linear trend versus frequency. Such an element was already mentioned by Larcher in [22].
 |
Fig. 7. Longitudinal viscosity versus temperature and frequency. |
In a second step, TTS was applied and longitudinal viscosity was plotted as a function of frequency and temperature on an enlarger frequency range. The results are shown in Figure 8 for TREF = 10, 30, 50°C. Curves were then adjusted with a Carreau-Yasuda law [13], where f is the frequency in Hz:
 |
Fig. 8. Longitudinal viscosity master curve and extrapolation to 110°C. |
with:
 where Ea = 140 kJ.mol−1 and T < 50°C
where Ea = 140 kJ.mol−1 and T < 50°C
ηo = 2.5e6 Pa.s, λ = 0.08 s and a = 0.70.
Remark: in a classical Carreau-Yasuda law, the exponent is not −1/a but (n − 1/a), where n is an adjustment coefficient. We found n = 0.
Above 50°C, Mouazen et al. [13] measured a lower activation energy between 110 kJ.mol−1 and 120 kJ.mol−1 resulting from asphaltens mobility increase. An extrapolation at 110°C is reported in Figure 8 with Ea = 115 kJ.mol−1. For such a temperature, bitumen seems to be Newtonian up to a few MHz. For Newtonian liquids it is admitted that, in a first approximation, the shear viscosity (generally measured with rheometers) can be linked to longitudinal viscosity with the simple relationship ηS ∼ ηL/3 (Trouton’s law) and we have demonstrated that it was verified for Newtonian liquids such as Glycerin, Honey, Fruit Juices, and sugar solutions [27, 28]. For bitumen studied at 110°C longitudinal viscosity of the first Newtonian plateau is estimated to ∼7 ± 4 Pa.s and this would lead toηS ∼ 2.5 ± 1.5 Pa.s.
Up to now, it is just a rough estimation which would have to be checked. For this purpose, high-temperature dedicated ultrasonic transducers will be needed. Nevertheless, such a value is in quite good agreement with values given in [35]. In this communication a value between 6 − 7 Pa.s is reported for T = 100°C Furthermore, an extrapolation of Newtonian viscosity given in [13] in the range 50 − 90°C to 110°C leads to 1.5 Pa.s which is in very good agreement with our ultrasonic estimation. In order not to overpass 150 Np.m−1 the corresponding frequency range is ∼1 − 2 MHz. Such a result could be surprising. Indeed, compared to lower temperatures viscosity is smaller but the maximum acceptable frequency for experimental cell No.3 remains around 1 − 2 MHz. In fact for lower temperatures we saw that the attenuation was linearly correlated to frequency because viscosity decreased as f−1 in the MHz frequency range. When temperature increases, the viscosity remains constant versus frequency and consequently, regarding relationship (5) the attenuation should evolve as ∼f2. Consequently, the viscosity decrease is compensated by the modification of the relationship between attenuation and frequency. So, the maximum acceptable frequency for experimental cell No. 3 should remain unchanged
4. Discussion
First of all, although our study primarily examined 70/100 bitumen, it is crucial to recognize that actual bituminized waste, like the STE3 sludge generated at La Hague, contains various salts such as BaSO4, NaNO3, PPFeNi, etc [4, 6, 7, 11] with different granulometry, density which could modify the conclusions obtained on pure 70/100 bitumen and perhaps perturb the ultrasonic method presented in this manuscript. A particular attention will have to be drawn to the inhomogeneous salt dispersion in bitumen. Further investigations will be needed to completely address this problem. In a first approximation, to facilitate experimentation and better simulate these complex mixtures, we prepared laboratory samples. Although our current research on these samples is not presented in this paper, specific samples comprise 60% bitumen, 27% BaSO4, and 13% NaNO3 representative of the dominant salts in STE3 sludge. These samples are similar to those produced by Mouazen et al. [11]. Preliminary tests conducted on this composite material, though not elaborated in this communication, suggest that ultrasonic parameters remain relatively consistent compared to pure 70/100 bitumen. Notably, these tests revealed heightened amplitudes in the ultrasonic signals transmitted through the cell. This increase in signal strength can be attributed to the notably high mass density of the sample’s components, especially 4500 kg.m−3 for BaSO4 and 2260 kg.m−3 for NaNO3. Since the mass density of this composite material surpasses that of pure bitumen, the difference in acoustical impedances (mass density × ultrasonic velocity) between the glass plates and the bi-salt/bitumen mixture is smaller than the difference for the glass plates and pure bitumen. Consequently, this results in a higher transmission coefficient of ultrasonic waves within the bi-salt/bitumen system, corroborating our initial findings. Importantly, to date, no direct comparisons have been drawn between the behaviour of bitumen and bi-salt bituminized products. Significantly, viscosity measurements of bi-salt asphalt performed by Mouazen [11–14] at low shear rates indicate a noticeable increase in viscosity. Furthermore, there are hints of heightened viscosity under irradiation conditions in Mouazen’s work [11]. These observations, primarily obtained at very low frequencies,necessitate assessment across a broader spectrum. Specifically, we must extend our analysis into the MHz frequency range at room temperature, encompassing γirradiation, and account for temperature variations to understand bubble migration dynamics up to 110°C. Of particular concern are structural modifications within the bitumen matrix, which could exert a considerable influence on ultrasonic parameters. Consequently, comprehensive further experiments are imperative to address these intricate issues definitively.
Secondly, our study pointed out that only frequencies in the range 1 − 2 MHz seem to be suitable for bitumen study. Indeed, we demonstrated that for higher frequencies, attenuation would be too high to correctly investigate 3.5 cm thickness cells. Working with smaller cells would not be adapted because we estimate that a representative volume for bubble nucleation investigation would not be reached. Regarding these values, millimetric wavelengths will have to be used for bubble detection. For millimetre-sized bubbles, the simple occultation of the ultrasonic beam should lead to the detection and the monitoring of bubble cloud rising. For instance, with the use of several in-lab designed, small-sized transducers settled on the cell, it would be possible to obtain the very first x–y mappings of bubble clouds. Better still, working with a system using an airborne coupling between sensors and cells would enable a rapid x–y scan to produce an x–y image of the system as a function of time. For smaller bubbles generated at lower irradiation rates, it is clearly established that they can have a significant effect on ultrasonic velocity and attenuation. So, using theoretical models [21, 36] it could be possible to deduce a distribution of bubble size in real time.
5. Conclusion
In this study, we investigated bitumen 70/100, commonly used in radioactive waste conditioning, using 500 kHz ultrasonic waves to assess the potential of acoustic approaches for monitoring radiolysis bubbles nucleation at room temperature and their migration up to 110°C. Measurements of ultrasonic velocities and attenuation around 500 kHz in the range 10 − 60°C led to ultrasonic attenuation and longitudinal viscosity (linked to shear viscosity) master curves establishment on a wide bandwidth thanks to the TTS application. A general behaviour law was established and showed that when temperature increases the first Newtonian plateau widens and that bitumen tends to a Newtonian behaviour up to a few MHz. With this behaviour law, acceptable ultrasonic frequencies have been estimated in the range 1 − 2 MHz. Such frequencies are well adapted to detect small bubble clouds with models correlating ultrasonic velocity or attenuation to void fractions or to directly follow bubbles with higher diameters of approximately a few millimetres.
Our ongoing work involves the investigation of bituminized samples containing bi-salts, which are more representative of bituminized radioactive waste. Furthermore, we are exploring the potential for direct monitoring under gamma irradiation, capitalizing on the operability of ultrasonic transducers in such conditions. These findings contribute to our understanding of how acoustic methods can be applied in the field of nuclear waste management, specifically in the monitoring and assessment of radiolysis processes. By using ultrasonic waves, we open doors to enhanced safety measures and a deeper comprehension of the behaviour of bituminized radioactive waste, which is invaluable for its long-term storage and disposal. Our research not only addresses current gaps in knowledge but also paves the way for further advancements in this critical field.
Acknowledgments
The authors sincerely acknowledge Total Energies for bitumen samples.
Funding
We received a grant from CNRS through its interdisciplinary programs (MITI) and from IRSN through its exploratory projects. The project (ARISE : Suivi ultrAsonore des gaz de Radiolyse des enrobés bItuméS lors d’incEndie) was selected in the framework of the (CNRS/IRSN) call for proposal “Matériaux, santé et mesures : au cœur des défis du nucléaire.”
Conicts of interest
The authors declare that they have no competing interests to report.
Data availability statement
All relevant data are given in the paper.
Author contribution statement
D. LAUX: funding acquisition, conceptualization, methodology, investigation, validation, software, formal analysis, supervision, writing, original draft K. TOULGOAT: investigation, software, writing – review & editing L. MILLOT, J-Y FERRANDIS: funding acquisition, conceptualization, methodology, investigation, validation, supervision, writing – review & editing.
References
- IAEA, Bituminization processes to condition radioactive wastes, Technical reports series, No 352 (1993) [Google Scholar]
- B. Nagy, F. Gauthier Lafaye, P. Holliger, D. J. Mossman, J. S. Leventhal, M. J. Rigali, Role of organic matter in the Proterozoic Oklo natural fission reactors, Gabon Africa Geol. 21, 655 (1993) [Google Scholar]
- J. C. Petit, Natural analogues for the design and performance assessment of radioactive waste forms: a review, J. Geochem. Explor., 46, 1 (1992) [CrossRef] [Google Scholar]
- J. Sercombe, F. Adenot, P. P. Vistoli, S. Parraud, C. Riglet-Martial, B. Gwinner, I. Felines, C. Tiffreau, M. Libert, Rapport Technique DTCD/2004/09. Dossier de référence bitume : synthèse des connaissances sur le comportement à long terme des colis bitumés (2004) [Google Scholar]
- K. Mijnendonckx, A. Van Gompe, I. Coninx, N. Bleyen, N. Leys. Radiation and microbial degradation of bitumen. MIND (Microbiology In Nuclear waste Disposal) Project. Grant Agreement: 661880. Deliverable 1.3 (2018) [Google Scholar]
- ASN, Revue externe sur la gestion des déchets bitumés. Rapport final (2019) [Google Scholar]
- IRSN. Avis relatif au dossier « Projet Cigéo – Dossier d’Options de Sûreté » (2017) [Google Scholar]
- W. Schorr, K. Starke, H. Dushner, Generation and diffusion of radiolysis gases in bituminized radioactive waste, Radiochim. Acta. 137, 133 (1977) [Google Scholar]
- N. K. Gulieva, G. M. Gatamkhanova, I. I. Mustafaev, Radiation resistance of bituminous waterproofing materials, High Energy Chem. 54, 336 (2020) [CrossRef] [Google Scholar]
- M. Mouazen, A. Poulesquen, B. Vergnes, Influence of thermomechanical history on chemical and rheological behavior of bitumen, Energy Fuels 25, 4614 (2011) [CrossRef] [Google Scholar]
- M. Mouazen, A. Poulesquen, F. Bart, B. Vergnes, Effect of γ irradiation on nuclear bituminized waste products (BWP): X-ray microtomography and rheological characterization, J. Nucl. Mat. 419, 24 (2011) [CrossRef] [Google Scholar]
- M. Mouazen, A. Poulesquen, F. Bart, J. Masson, M. Charlot, B. Vergnes, Rheological, structural and chemical evolution of bitumen under gamma irradiation, Fuel Proc. Tech. 114, 144 (2013) [CrossRef] [Google Scholar]
- M. Mouazen, A. Poulesquen, B. Vergnes, Correlation between thermal and rheological studies to characterize the behavior of bitumen, Rheol. Acta 50, 169 (2011) [CrossRef] [Google Scholar]
- M. Mouazen, A. Poulesquen, B. Vergnes, Caractérisation rhéologique de bitume 70/100 utilisé comme matrice de confinement de déchets radioactifs, 44ème Colloque annuel du Groupe Français de Rhéologie, Strasbourg (2009) [Google Scholar]
- A. Marchal, B. Vergne, A. Poulesquen, R. Valette, Competitive growth and rising of bubbles in a yield stress fluid. Consequences on the macroscopic swelling of bitumen drums, J. Nonnewton. Fluid Mech. 234, 162 (2016) [CrossRef] [Google Scholar]
- F. Koksel, M. G. Scanlona, J. H. Page, Ultrasound as a tool to study bubbles in dough and dough mechanical properties: A review, Food Res. Int. 89, 74 (2016) [CrossRef] [Google Scholar]
- M. J. W. Povey, T. J. Mason, Ultrasound in food processing. (Blackie Academic, 1992) [Google Scholar]
- F. S. Crawford. The Hot Chocolate Effect, Am. J. Phys. 50, 398 (1982) [CrossRef] [Google Scholar]
- P. S. Wilson, R. A. Roy, An audible demonstration of the speed of sound in bubbly liquids, Am. J. Phys. 76, 975 (2008) [CrossRef] [Google Scholar]
- Z. Travnicek, A. I. Fedorchenko, M. Pavelka, J. Hruby, Visualization of the hot chocolate sound effect by spectrograms, J. Sound. Vibr. 331, 5387 (2012) [CrossRef] [Google Scholar]
- L. D’Hondt, M. Cavaro, C. Payan, S. Mensah. Acoustical characterisation and monitoring of microbubble clouds, Ultrasonics 96, 10 (2019) [CrossRef] [Google Scholar]
- N. Larcher, Contribution à la caractérisation des matériaux au comportement viscoélastique par méthode ultrasonore. Application aux matériaux bitumineux, Thèse de l’Université de Limoges (2014) [Google Scholar]
- A. Rabbani, D. R. Schmitt, Ultrasonic shear wave reflectometry applied to the determination of the shear moduli and viscosity of a viscoelastic bitumen, Fuel 232, 506 (2018) [CrossRef] [Google Scholar]
- A. Rabbani, D. R. Schmitt, The longitudinal modulus of bitumen: Pressure and temperature dependencies. Geophysics 84, 139 (2019) [Google Scholar]
- D. Laux, G. Chabanol, G. Sapey, J-Y. Ferrandis, E. Rosenkrantz, Shear and Longitudinal attenuations and quality factors of poly(methyl metacrylate) (PMMA) from 20 kHz to 12 MHz investigation with ultrasonic spectroscopy, Ultrasonics 134, 107104 (2023) [CrossRef] [Google Scholar]
- J. E. Carlson, J. Van Deventer, A. Scolan, C. Carlander, Frequency and temperature dependence of acoustic properties of polymers used in pulse-echo systems, IEEE Symp. Ultrason. 1, 885 (2003) [Google Scholar]
- D. Laux, M. Valente, J-Y. Ferrandis, N. Talha, O. Gibert, A. Prades, Shear viscosity investigation on mango juice with high frequency longitudinal ultrasonic waves and rotational viscosimetry, Food Biophys., 8, 233 (2013) [CrossRef] [Google Scholar]
- M. A. Mograne, J-Y. Ferrandis, D. Laux, Instrumented test tube for rapid rheological behaviour of liquids estimation, J. Food Eng. 247, 126 (2019) [CrossRef] [Google Scholar]
- A. S. Dukhin, P. J. Goetz, Bulk viscosity and compressibility measurement using acoustic spectroscopy, J. Chem. Phys. 130, 124519 (2009) [CrossRef] [Google Scholar]
- G. Lévêque, E. Rosenkrantz, D. Laux, Correction of diffraction effects in sound velocity and absorption measurements, Meas. Sci. Technol. 18, 3458 (2007) [CrossRef] [Google Scholar]
- A. M. Bianchi, Y. Fautrelle, J. Etay, Transferts Thermiques. Presses polytechniques et Universitaires romandes (2004) [Google Scholar]
- J. D. Ferry, Viscoelastic Properties of Polymers, Third Edition (John Wiley & Sons, 1980) [Google Scholar]
- G. Schramm, A Practical Approach to Rheology and Rheometry, 2nd edn. (Thermo Electron, 1994) [Google Scholar]
- R. Tanaka, E. Sato, J. E. Hunt, R. E. Winans, S. Sato, T. Takanohashi, Characterization of asphaltene aggregates using X-ray diffraction and small-angle X-ray Scattering, Energy Fuels 18, 1118 (2004) [CrossRef] [Google Scholar]
- J. Ekblad, R. Lundström, E. Simonsen, Water susceptibility of asphalt mixtures as influenced by hydraulically active fillers, Mat. Struct. 48, 1135 (2015) [CrossRef] [Google Scholar]
- K. W. Commander, A. Prosperetti, Linear pressure waves in bubbly liquids: Comparison between theory and experiments, J. Acoust. Soc. Am. 85, 732 (1989) [CrossRef] [Google Scholar]
Cite this article as: Didier Laux, Killian Toulgoat, Lucie Millot, Jean-Yves Ferrandis. Rheological investigation of bitumen, used for radioactive waste conditioning, with ultrasonic waves, EPJ Nuclear Sci. Technol. 10, 1 (2024)
All Tables
All Figures
 |
Fig. 1. Bitumen cells with 3 different thickness designed with 3D printing. |
| In the text | |
 |
Fig. 2. Experimental bench (cell + transducers) in the thermoregulated chamber. |
| In the text | |
 |
Fig. 3. Mean cell No.3 temperature as estimated with ultrasounds. |
| In the text | |
 |
Fig. 4. (a) Ultrasonic properties of bitumen 70/100 compared to 35/50 bitumen data (a) velocity vB (b) attenuation αBW. |
| In the text | |
 |
Fig. 5. Ultrasonic attenuation in 70/100 bitumen for T = 20°C, after TTS application on data measured with 500 kHz transducers and comparison with direct estimations, using 1 MHz and 2.25 MHz sensors. |
| In the text | |
 |
Fig. 6. ln(aT) versus (1/T − 1/TRef) for TRef = 20°C and linear adjustment for activation energy determination. |
| In the text | |
 |
Fig. 7. Longitudinal viscosity versus temperature and frequency. |
| In the text | |
 |
Fig. 8. Longitudinal viscosity master curve and extrapolation to 110°C. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.









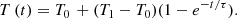




![$$ \begin{aligned} {\eta }_{L}\left( f \right)=a_{T}.{\eta }_{o}\left[ 1+\left(\lambda .a_{T}.f\right)^{a} \right]^{-1/a} \end{aligned} $$](/articles/epjn/full_html/2024/01/epjn230031/epjn230031-eq20.gif)