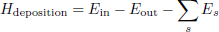EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 10 (2024) EPJ Nuclear Sci. Technol., 10 (2024) 24 Full HTML
Issue
EPJ Nuclear Sci. Technol.
Volume 10, 2024
Status and advances of Monte Carlo codes for particle transport simulation
Article Number 24
Number of page(s) 14
DOI https://doi.org/10.1051/epjn/2024021
Published online 11 December 2024

© K. Wang et al., Published by EDP Sciences, 2024

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

High-fidelity simulations are essential and irreplaceable in the accurate and reliable analysis of nuclear energy systems, especially in the design and analysis of new types of nuclear reactors in the recent decade. In advanced and innovative types of nuclear systems, such as the small modular reactors, mobile micro-reactors, and nano-reactors, traditional reactor physics calculation methods and codes based on spatial and spectral approximations and homogenization are being challenged due to “irregular” geometry, unconventional energy spectrum and strong anisotropy in new designs [1–3]. In this circumstance, the Monte Carlo method plays a more vital role in both neutronics and multi-physics coupling simulations. Accompanied by the development of supercomputer technology and parallel acceleration and optimization methods, the Monte Carlo method has become the prevailing approach for high-fidelity nuclear reactor analysis [4–6].

As a self-developed Monte Carlo code since 2000 by the REAL (Reactor Engineering Analysis Laboratory) team in the Department of Engineering Physics at Tsinghua University, the Reactor Monte Carlo code (RMC) [7] has become a powerful and innovative simulation platform for nuclear reactor analysis and beyond. Based on the comprehensive introduction in the last SNA+MC conference in 2013 [8], more advanced features and powerful functions have been developed and added to RMC, such as the stochastic and continuous-varying media modeling, advanced transient simulation capability, more accurate energy deposition model and many others. Beyond basic neutronics calculation for nuclear reactors, RMC has also been applied in shielding analysis, criticality safety analysis, and numerical simulation for fusion systems [9, 10]. Equipped with coupling simulation capabilities among neutronics, thermal-hydraulic, and mechanics, RMC is being developed into a powerful simulation platform that can facilitate the design and analysis of innovative nuclear systems.

thumbnail Fig. 1.

Octree-Based Acceleration in RSA (left) and simplified algorithm illustration of the Iterative RSA-DEM Method (right).

This paper reviews the main features developed in the RMC code in recent years and introduces ongoing research projects and future development plans. Section 2 introduces the new geometry modeling capabilities in RMC. Sections 3 and 4 are on the advances of RMC in advanced reactor physics calculations, including transient simulations and new algorithms, etc. Section 5 contains the multi-physics coupling research and applications in practice, including examples of the comprehensive RMC and multi-physics coupling platform in new types of reactor design and analysis. Lastly, Section 6 concludes the technical advances and application cases in RMC and discusses future research plans.

2. Modeling capabilities

As the vital feature for high-fidelity numerical simulations, the modeling capability, especially concerning the geometry, is at the very heart of advanced Monte Carlo methods.

2.1. Stochastic media

Stochastic media like random fuel pebbles and TRISOs are widely used in new types of nuclear reactors [11]. Various capabilities have been developed in RMC for the simulation of neutron transport in stochastic media [12, 13], of which there are six primary stochastic geometry modeling methods: (1) Chord Length Sampling (CLS), (2) Random Lattice Method, (3) Random Sequential Addition (RSA) [14], (4) Distinct Element Method (DEM), (5) Iterative RSA-DEM Method [14, 15] and (6) Optimized Drop and Roll – Virtual Surface (ODR-VS) Method [16]. Of particular note are the innovations made in the latter four stochastic geometry modeling methods.

The CLS Method is the only implicit method for stochastic media in RMC; it approximates neutron transport through stochastic media without the explicit generalization of the media itself. The Random Lattice Method involves generating particles within the boundaries of the cells of a lattice whilst exacting random translations on the particles to develop a stochastic geometry [12]. In the RSA Method, particles are added to the stochastic media randomly without overlap until the desired particle packing fraction is achieved; an improved RSA algorithm was developed by employing octree-based acceleration, as shown in the left part of Figure 1 [13]. The improved algorithm can produce highly accurate results with significantly reduced simulation time, with the capability to be easily adapted for different nuclear fuel configurations. The Iterative RSA-DEM Method developed in RMC couples the improved RSA and DEM methods to solve the high computational requirements of the DEM method, and the main steps are illustrated in the right part of Figure 1. The ODR-VS method is an explicit modeling method that combines the Optimized Dropping and Rolling (ODR) method and the Virtual Surface (VS) method for simulating no-contact dispersed particle models with packing fractions above the RSA infinite-time saturation limit of 38%.

2.2. Continuously varying media

In the advanced and novel concept reactors such as liquid-fuel reactors and supercritical water-cooled reactors, the capability of modeling continuous material properties is important to accurately take into account the physical parameters of the fuel solution in the Monte Carlo transport. In RMC the Continuously Varying Material Transport (CVMT) method is proposed using an improved direct sampling method [17–19] based on a new numerical integration method for three-dimensional space [20]. The Direct Sampling and the RayTracking methods are combined in our implementation depending on the material property as illustrated in Figure 2.

thumbnail Fig. 2.

Illustration of the mixed-transport method in uniform and continuously-varying materials.

A 3-D fuel rod model with finely layered uniform material is tested as shown in Figure 3. The mixed-transport method of CVMT and direct sampling can make the RayTracking process in RMC more general as well as improve computational efficiency. Numerical results show that the CVMT method in RMC can directly simulate the continuous material problem with higher accuracy than the layered uniform material model.

thumbnail Fig. 3.

Radial diagram and simulation results of continuous material distribution of test fuel rod.

2.3. CAD-based neutron transport

Computer-aided design (CAD) is a powerful tool for geometry construction and modeling. RMC is capable of processing CAD models and support the definition of weight window and cell importance parameters. The implementation scheme of CAD capability in RMC adopts three layers, including the RMC main module, an interface layer, and the open-source software package DAGMC module [21], which consists of the Mesh-Oriented datABase (MOAB) and Common Geometry Module (CGM). An extensive validation of various problems has been conducted using the CAD-based transport in RMC [22].

Figure 4 shows two CAD models used in RMC simulations, including the simplified Heat Pipe Reactor (HPR) [3] and the fusion tokamak model SUNIST-2 (Sino-UNIted Spherical Tokamak) designed and built by the fusion team in Tsinghua University [23].

thumbnail Fig. 4.

CAD-based models for neutron transport simulations using RMC. (a) Heat Pipe Reactor (HPR), (b) Sino-UNIted Spherical Tokamak (SUNIST-2).

3. Advancements in basic neutronics analysis

3.1. An Innovative Structure (AIS) database

The nuclear database in RMC is shifting from traditional ACE to An Innovative Structure (AIS) database based on the HDF5-format file system [24]. To improve the readability and extensibility of the nuclear database used by RMC and save disk space occupation, a hierarchical structure nuclear database was designed in AIS. Additionally, a Python code package was developed to parse ACE databases and generate AIS based on the hierarchical structure. The resulting AIS nuclear database offers significantly enhanced readability and extensibility. By eliminating redundant data in the ACE nuclear database and leveraging the compression characteristics of HDF5 files, a significant reduction in disk space usage is achieved compared to ACE databases. The thermal neutron nuclear database exhibits a 60% reduction, while the continuous energy neutron nuclear database achieves an 80% reduction in disk space consumption compared to the LANL’s decimal ACE database based on ENDF/B-VIII.0. The application of the HDF5-format neutron nuclear database was achieved under the RMC criticality calculation mode. Furthermore, criticality calculations of VERA benchmark problem 2B were conducted using both the HDF5-format nuclear database and the ACE nuclear database. The calculation results demonstrate that both the keff and cell neutron flux counts obtained from the two approaches were in perfect agreement, providing evidence for the correctness of the HDF5-format nuclear database and the correctness of the application development of RMC. Furthermore, the computational results indicate that the criticality calculations based on the HDF5-format neutron nuclear database exhibit a 46.5% reduction in memory usage and a 5.1% improvement in computational efficiency compared to those based on the ACE neutron nuclear database. The ongoing research is underway to further achieve compatibility with other functions of RMC code.

3.2. Homogenization and multi-group constants generation

Full capabilities of generating multi-group constants have been built in RMC, which can be used for lattices or assembly homogenization calculation, and provide the homogeneous few group constants for core simulations. At present, the RMC homogenization function includes a few-group macroscopic cross-section generation module, a few-group microscopic cross-section generation module, B1 approximation for leakage correction module, SPH equivalent correction module, and core coupling interface module [25]. In the homogenization module, the super homogenization method directly adjusts the group constants to ensure the conservation of the reaction rate before and after homogenization.

The homogenization function can be modeled according to the user defined fuel element to achieve the user specified area of the homogenization process. The geometry processing can cover the rod/grid/hexagonal/rectangle/sector and other common geometric shapes. The homogenization methods cover common homogenization methods such as global, lattice, and designated area homogenization.

3.3. Depletion and burnup calculation

The depletion module embedded in the RMC code, DEPTH, employs ORIGEN-2 and ORIGEN-S-based data libraries enables users to assign problem-dependent libraries for each depletion step [26–28]. Algorithms for handling stiff depletion systems are developed in RMC, such as Transmutation Trajectory Analysis (TTA), Chebyshev Rational Approximation Method (CRAM), Quadrature-based Rational Approximation Method (QRAM), and Laguerre Polynomial Approximation Method (LPAM).

Through the neutronic transport module and point-depletion module, various neutronic-depletion coupling schemes can be implemented by transferring neutronics parameters and nuclear density parameters between modules in different ways. To enhance the performance of burnup calculation, RMC has developed several neutronic-depletion coupling schemes. These schemes aim to achieve better performances while considering factors such as accuracy, efficiency, and numerical stability, including (a) beginning of step approximation, (b) predictor-corrector on nuclides densities, (c) predictor-corrector on micro one-group reaction rates, (d) high order predictor-corrector, (e) sub-step method, (f) extended predictor-corrector, (g) explicit linear sub-step method, and (h) implicit linear sub-step method.

These coupling schemes cater to different problem-solving needs, with each having its benefits. For instance, method (g) excels in Gd-bearing problem scenarios, demonstrating superior performance. Conversely, method (h) based on the implicit Euler method enhances numerical stability and accuracy. The potent combination of the embedded depletion module DEPTH, along with domain decomposition, a parallel depletion solver, and coupling schemes, empowers RMC with powerful capabilities for burnup calculations.

thumbnail Fig. 5.

The SF96 lattice benchmark model (left) and power distribution and uncertainty computed using RMC (right).
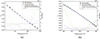thumbnail Fig. 6.

Comparison of the predicted fuel temperature reactivities using perturbation coefficients and the directly calculated results. (a) PWR fuel (T at 900 K), (b) HPR fuel (T at 1000 K).

3.4. Sensitivity and uncertainty analysis

Sensitivity and uncertainty analyses constitute integral components of high-fidelity nuclear reactor simulations. RMC is capable of calculating the sensitivities of different responses to nuclear data and geometry parameters. The responses include keff [29], reaction rate ratios [30], reaction rates [31] and kinetic parameters. RMC uses Iterated Fission Probability (IFP) and the general perturbation method to calculate sensitivities and then calculates the uncertainties using the “sandwich rules” [32]. A noteworthy feature of RMC involves the integration of the super history method into both IFP and general perturbation methodologies, a measure implemented to optimize memory usage. A super history comprises an ancestral particle and its subsequent progeny, categorized into distinct generations, with the general adjoint flux computed across all descendant histories. Furthermore, RMC exhibits versatility in addressing various forms of geometry perturbations, encompassing homogeneous expansion, unidirectional expansion, and fixed-axis rotation, among others, thereby enhancing its applicability in geometry sensitivity analyses [33].

The numerical tests use the SF96 lattice model derived from the Takahama-3 pressurized water reactor (PWR) in Japan as depicted in the left in Figure 5 [34]. As an extension to the right part of the figure showing the analysis of power uncertainties, there is a concurrence in the estimations of power distribution uncertainties derived through the first-order uncertainty quantification method and those obtained via the stochastic sampling method. The relative differences between the two methodologies are within 8% [31].

3.5. Material perturbation

The second-order material density and temperature perturbation have been implemented in the RMC code [35]. The implementation is based on the differential operator method, and its main task is to perform cross-sectional online derivation during the neutron transport process. The material density perturbation considers the effect of the material density on the macroscopic cross-section, while the material temperature perturbation considers the effect of the material temperature on the microscopic cross-section, that is, the Doppler effect.

Currently, the material perturbation function in RMC supports response quantities of keff and power. The effectiveness of the material density perturbation function is demonstrated in the reactivity-density coefficients problems of PWR moderator and HPR reflectors. Figure 6 shows that the calculated perturbation coefficients can be used to accurately predict the reactivity accurately over a wide range of boron concentrations of the PWR moderator and a wide range of temperatures of HPR reflectors.

4. Advanced physics features

4.1. Transient simulations

Both the Direct Kinetics Simulation (DKS) and Predictor-Corrector Quasi-Static (PCQS) methods are implemented in RMC [36, 37], and the connection method which combines both of them is tested and proven to improve the calculation efficiency while maintaining high accuracy.

The probability of survival (POS) is a quantity computed in stochastic kinetics and is also a simple index to test the correctness of the method of describing weak source systems. Simulation results are compared in the left part of Figure 7, including the RMC calculation results based on the single neutron tracking method and the neutron bank tracking method, and the MCATK calculation results.

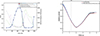thumbnail Fig. 7.

Comparison of transient simulation results in weak (left) and strong (right) neutron fields.

During the startup process of the reactor without an external neutron source, the reactor initially contains a weak neutron field composed of spontaneous fission in the fuel, which can only be simulated by the DKS method. When the number of neutrons increases to a strong neutron field, it can be simulated with the faster PCQS method. It is initially calculated by the DKS method and then calculated by the PCQS method.

Currently, international research has only conducted coupling calculations between the two theories (stochastic neutron kinetics and the Boltzmann transport method) for point reactor models. There is a lack of published research on addressing three-dimensional complex geometrical systems. We investigate the connection computation of Monte Carlo DKS method and PCQS method based on RMC code. It achieves the three-dimensional simulation of the connection calculation between the DKS method in a weak neutron field based on stochastic neutron transport equation and the PCQS method in a strong neutron field based on a time-dependent Boltzmann neutron transport equation. The comparison of the calculation results of the three methods in the whole process is shown in the right part of Figure 7, including the pure DKS method, the pure PCQS method, and the DKS method connected with the PCQS method, which are in good agreement.

4.2. Energy deposition

A new energy deposition treatment was recently developed in RMC [38] which features a most accurate mode with coupled neutron and photon transport. In this mode, neutrons and photons are independently transported and their energy is deposited far away from the reaction site.

In this case, the neutron KERMA is calculated as:

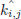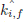k i , j = ( k i , j ̂ − k i , f ̂ ) + ( Q fragments + Q β , d ) σ i , f ( E ) $$ \begin{aligned} k_{i,j} = (\hat{k_{i,j}} - \hat{k_{i,f}}) + (Q_{\rm fragments} + Q_{\beta , d})\sigma _{i,f}(E) \end{aligned} $$(1)

where k i , j ̂ $ \hat{k_{i,j}} $ and k i , f ̂ $ \hat{k_{i,f}} $ are the total KERMA and fission KERMA which are directly generated by NJOY. Qfragments and Qβ, d are the energy of fission fragments and delayed β. It is noted that the delayed β energy generated in a fission reaction is included which is artificially neglected in NJOY [39].

Different from neutron, the photon energy deposition is calculated using the collision estimation method instead of the photon KERMA, which is expressed as:

H deposition = E in − E out − ∑ s E s $$ \begin{aligned} H_{\rm deposition} = E_{\rm in} - E_{\rm out} - \sum _{s} E_{s} \end{aligned} $$(2)

where Ein and Eout are the energy of the incoming and outgoing photons, respectively. Es is the energy of the secondary particles including the photons, electrons, and positrons. Benefit from a new photon transport capacity implemented in RMC [40], all these secondary particles are transported physically and their energy deposition is also calculated using equation (2).

The most accurate model with coupled neutron and photon transport is verified using three typical PWR problems from the VERA benchmark against the references from MCNP [41], Serpent [42], and OpenMC. High-level comparisons of the energy deposition in different materials and fission components are performed, demonstrating excellent agreement with minor differences observed (See Tab. 1).

Table 1.

Energy deposition in different materials for VERA2G in MeVs.

Figure 8 further compares the normalized energy release (mode 1), energy deposition (mode 4), and gamma deposition for VERA2G and VERA2P cases. The energy deposition generally follows the distributions of the energy release in the fuel regions. In the guide tubes, the energy deposition is much higher than the capture energy release, primarily due to the deposited energy of gammas produced in fission. However, notable differences are observed in the Ag-In-Cd control rods and Gd burnable poison rods. In these regions, the energy deposition is lower than the energy release. This is because the capture gammas produced in (n, γ) reactions tend to deposit their energy away from the site of origin.

thumbnail Fig. 8.

Comparison of the normalized energy release energy deposition, and gamma deposition for VERA2G, VERA2P. The color of each cell is determined by the amount of the gamma energy deposition. (a) 2G, (b) 2P.

4.3. Shielding calculation

Deep-penetration problems are technically challenging to simulate and optimize in shielding calculations. Optimizations and newly developed mathematical and computational techniques to perform shielding calculations for the deep-penetration problem have been implemented in both published and underway research in RMC [43, 44].

Two types of mesh-based weight windows are implemented in RMC to perform variance reduction (VR). One is designed as the foundation of RMC VR ability and is compatible with the most widely used mesh-based weight window. The other one is upgraded for the penetration calculation with fine mesh and short particle average free-fly distance. With these two types of weight windows, we can perform shielding calculation in more diversified conditions thus elevating the capability of shielding calculation in RMC.

We also developed a weight window optimizer in RMC to make an effective variance reduction process. In this program we re-invented the weight window generator and expanded its usage to optimization of parameters. In RMC, we can perform weight window parameter updates along with particle transportation and after certain batches of source simulation, we can optimize the parameters to an acceptable level for deep-penetration problems.

Besides, in computational construction we have optimized data structures and algorithms to perform particle splitting and mesh-based weight window generation based on Monte Carlo. Adaptive MPI and OpenMP parallelism for acceleration is applied in RMC to balance time and memory cost.

4.4. Neutron multiplicity simulation

Two methods for the simulation of neutron multiplicity counting have been developed in RMC. The first method involves utilizing the capture output feature in particle output events to obtain the neutron capture time in a specified cell for a specified nuclide. Neutron multiplicity counting is then obtained through processing using a multiplicity shift register. The second method involves conducting a temporal analysis of neutrons captured in a specified cell for a specified nuclide at the end of each neutron history. This method also yields neutron multiplicity counting and commonly referred to as the “PTRAC” method.

HLNC2, the new upgraded version of the High-Level Neutron Coincidence Counter (HLNCC) developed by Los Alamos National Laboratory (LANL) [45], was used for verification in RMC. The detector contains 18 3He tubes in a cylindrical polyethylene body. The schematic diagram of RMC modeling is shown in Figure 9.

thumbnail Fig. 9.

Layout of the HLNC2 model in RMC simulation.

Table 2.

Neutron Multiplicity Countings Results (with the mass of 695.04 g of 240Pu).

Pu with the same mass as in the literature was selected for calculation. PuO2 is a cylinder with a height of 20 cm and a radius of 5 cm, and its density is 2.5 g/cm3. The calculated mass of 240Pu that can be obtained is 695.04 g. The chosen pre-delay time is 450 shakes, and the gate width is 6400 shakes. From Table 2, it can be observed that the relative deviations between the results calculated by RMC and MCNP are all within 5%, demonstrating the accuracy of the RMC calculations. The term “RMC-cap” in the Table 2 represents results calculated using a temporal analysis of neutrons captured in a specified cell for a specified nuclide at the end of each neutron history and “RMC-ptrac” denotes results obtained using particle capture events output and processed through a multiplicity shift register.

4.5. Functional Expansion Tallies (FET)

The Functional Expansion Tallies (FET) method is advantageous for computing the continuous distribution of parameters in the solution space and can solve the problem of the coexistence of computational efficiency and precision [46–49]. An innovative FET method based on track-length estimation is proposed and implemented in RMC [50]. In addition, the Legendre polynomials and Zernike polynomials are combined to calculate a continuous distribution of the parameters in a three-dimensional cylindrical space. Moreover, to solve the numerical instability of the FET method on the boundary of the tally region, we propose a track-length cutting method. The new FET method in RMC can obtain a continuous distribution of the parameters in cases of a 10%–80% reduction in computing time compared with the finely divided mesh tally method. The method can also solve the problem where the traditional mesh tally method occupies too much simulation memory. Therefore, the new FET method can obtain more accurate results with less simulation memory (less than 10%). For example, Figure 10 shows a fuel rod cylindrical two-dimensional model. The radial flux distribution of the fuel rod model is calculated by 6 × 6 meshes tally and FET method, the flux distribution is shown in Figure 11.

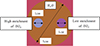thumbnail Fig. 10.

Two-dimensional cylinder model.
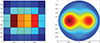thumbnail Fig. 11.

Mesh tally and FET results in contrast.

Besides, we also use the new FET method in the source convergence diagnosis method and nuclear thermal-physics coupling.

In order to acquire no-mesh distribution of fission source [51, 52], we proposed the FET source convergence diagnosis method in RMC [53]. Due to the randomness in Monte Carlo calculations and the difficulty in determining the precise source convergence, a reliable and stable convergence judge method is presented as a solution. The FET method is able to decrease the number of inactive cycles, which greatly decreases the calculation time by 40%. For example, Figure 12 shows a three-dimensional source convergence benchmark proposed by OECD/NEA. The initial source distribution and convergent source distribution are also shown in this figure. It can be seen that the FET method can obtain a no-mesh distribution of fission sources.

thumbnail Fig. 12.

The schematic diagram and initial source distribution and convergent source distribution of the three dimensional source convergence benchmark.

Concerning thermal-physics coupling, precise and effective transfer of data between different meshes is a difficult challenge. Converting two separate meshes and transferring the data is an exceptionally difficult and complex task within the conventional nuclear thermal-physics coupling approach [54, 55]. By applying FET method to nuclear thermal-physics coupling, the no-mesh continuous fission energy distribution can be obtained, which is suitable for more complex meshes. Additionally, the computational memory can be minimized by substituting the data from numerous mesh power distribution data points with the coefficients of the function. In this work, RMC is coupled to SUBCHAN using the new FET coupling framework with an in-house Python script developed for the coupling of a neutronic code and a thermal-hydraulic one, as shown in Figure 13 and described below.

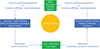thumbnail Fig. 13.

FET nuclear thermal-physics coupling flow chart.

4.6. Source convergence diagnosis

Previous studies have shown that random error term in the power iteration process significantly influences the source convergence diagnosis and variance underestimation phenomenon [56, 57]. In RMC the Sliced Wasserstein (SW) distance of the fission source distributions (FSDs) is used to estimate the error terms in the power iteration process. Three mesh-free SW-based methods are proposed to capture the random error term’s 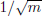1 / m $ 1/\sqrt{m} $ feature for the OECD source convergence fissile slab model, sphere array model, and the BEAVRS model, based on which a mesh-free source convergence auto-diagnosis algorithm is developed and tested [58]. Numerical calculation results show that the auto-diagnosis algorithm is practical and efficient for source convergence diagnosis and acceleration, which can automatically save 58%–81% of the computational time to reach a converged fission source in models with a dominance ratio of around 0.99. Figure 14 illustrates the evolution of FSD SW distances with the increasing neutron histories in the BEAVRS core model. The fission source converges after simulating around 270 million neutron histories using the conventional Power Iteration method. By contrast, the 5-stage auto-diagnosis method uses only 60 million neutron histories to realize automatic convergence diagnosis, reducing 81% of the computational time.

thumbnail Fig. 14.

The FSD SW distance evolution with neutron history [58].

5. Multi-physics coupling and applications

5.1. RMC + SUBCHAN

RMC is coupled with the sub-channel code SUBCHAN developed in the Department of Engineering Physics at Tsinghua University [59, 60] using the loose coupling scheme and validated on the BEAVRS benchmark. Unlike previous RMC/CTF coupling methods, a new loose coupling framework is developed based on the Picard iteration scheme and pin-wise data transfer technique.

As depicted in Figure 15, this process involves calling RMC and SUBCHAN one after and generating four external files. Two interface functions, RMC2SUBCHAN and SUBCHAN2RMC, are developed to facilitate data transfer between RMC and SUBCHAN. In the iteration loop, the loose coupling scheme starts by invoking RMC, which generates a 3-D power distribution in the MeshTally.h5 file. This power distribution is either obtained from the previous iteration or consists of initial guess values in the first iteration.

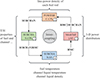thumbnail Fig. 15.

Workflow of the file-based coupling in each Picard iteration.

The calculation of Criticality Boron Concentrations (CBC) values is performed at hot full power (HFP) and All Rods Out (ARO) conditions. The CBC results for two cycles are presented in Figure 16.

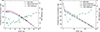thumbnail Fig. 16.

CBC evaluations of BEAVRS cycle 1 (left) and cycle 2 (right).
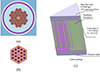thumbnail Fig. 17.

RMC and Fluent models of the micro gas-cooled reactor. (a) RMC model for the core, (b) RMC model for the fuel assembly, (c) 1/8 model using Fluent.

5.2. RMC + Fluent

More multi-physics coupling work of neutronics and T/H has been explored and tested using RMC and other T/H codes such as CTF, ANSYS CFX and Fluent. Presented here is recent research on gas-cooled micro reactors and plate fuel reactors using the coupling of RMC and Fluent.

Gas-cooled micro reactors using prismatic fuel assemblies have got wide attention as one of the fourth-generation reactor types. In previous research, ANSYS Fluent was selected as the T/H solver and the coupling framework of RMC-Fluent was developed, as illustrated in Figure 17. This coupling framework can carry out high-precision, multi-scale coupling calculations of steady-state physics and T/H calculations on the micro gas-cooled reactor core, and is an important tool for core design and safety analysis.

5.3. RMC + OpenFOAM

Traditional reactor analysis design tools are challenged when modeling solid-core reactors, such as the Heat Pipe-cooled Reactors (HPR) which use a metallic substrate and enclosed high-temperature heat pipes for heat conduction. To solve this challenge, the neutronics-heat transfer-mechanics coupling framework based on RMC and OpenFOAM is developed and tested in applications of the HPR simulation [61–63]. In this method, sub-region mapping based on spatial location is adopted to transform parameters between RMC and OpenFOAM. To achieve multiphysics coupling, a user-defined solver named thermalMechanicsFoam is built based on a built-in transient solver named solidDisplacementFoam in OpenFOAM. This method considers power changes, thermal expansion, heat pipe operation, thermal contact conduction, and gap thermal resistance. It also takes into account the reactivity feedback caused by the redistribution of the working fluid in the alkali metal heat pipes.

thumbnail Fig. 18.

The RMC and OpenFOAM model for the KRUSTY reactor.
thumbnail Fig. 19.

Reactivity and relative power variation (left) and temperature distribution (right) during the transient process.

A typical HPR model, KRUSTY, was used in the coupling research of RMC and OpenFOAM as illustrated in Figure 18 [64, 65]. The calculation results are in good agreement with the load-following test results, demonstrating the effectiveness of the proposed method. Furthermore, the self-regulating capability of such reactor systems was investigated, and a hypothetical accident was simulated. Assuming that the radiator experiences a loss at the beginning of the accident, the reactor system returns to normal after 1500 seconds of transient. In this hypothetical accident, the control rods remain outside the core, and the reactor solely relies on reactivity feedback to adjust the fission power. According to the simulation results shown in Figure 19, the peak temperature is only about 1112 K, far below the safety limit. In terms of system recovery, the reactor takes about 2500 seconds to return to steady state and can effectively adjust the power through reactivity feedback. This study confirms the effectiveness of the coupling method, which can be used as an effective tool for simulating heat pipe-cooled reactors.

6. Conclusions and future plan

Based on academic research and industrial applications over more than 20 years in China, RMC has become a powerful, innovative and versatile simulation platform for nuclear reactor analysis, criticality safety calculations, fusion neutronics simulations and beyond. Deployed in many world-class supercomputers in China, RMC played an important role in the design and analysis of commercial nuclear power plants and newly designed types of advanced nuclear reactors. The neutronics-thermal hydraulics-mechanics coupling capability enables RMC to simulate high-fidelity multi-physics problems and transient scenarios. In this paper the main advancements and features of RMC are introduced with applications on the simulation of advanced reactors. The state-of-the-art technologies developed in RMC in recent years are reviewed, such as stochastic and continuous-varying media modeling, advanced transient simulation capability, more accurate energy deposition model, etc.

With the rapid development of heterogeneous-architecture supercomputers such as the GPUs by Intel and NVIDIA and SW in China, ongoing and future work based on RMC will put more effort in the acceleration and optimization of heterogeneous parallel architectures. Machine learning algorithms will also be incorporated in ongoing research and future development plans.

Acknowledgments

The authors want to thank all the funding sources which support the research and development of RMC during these years, including but not limited to those listed in the Funding section. The authors also want to thank Professor Yi Tan and Professor Long Zeng in the Department of Engineering Physics at Tsinghua University for the CAD model of SUNIST-2 used in this article. Lastly and most importantly, all REAL alumni (“REALers”, more than 100 over the 20 years) are to be acknowledged for all their hard work and contribution in the development, maintenance and promotion of RMC in both academia, industry and education.

Funding

National Natural Science Foundation of China (No. 91126017, 11475098, 11605101, 11775127, 11775126), National Key Research and Development Program (No. 2020YFB1901700), Science Challenge Project (No. TZ2018001), Science and Technology on Reactor System Design Technology Laboratory, etc.

Conflicts of interest

The authors declare that they have no competing interests to report.

Data availability statement

This article has not generated nor analyzed data associated with this article.

Author contribution statement

Kan Wang: Conceptualization, Supervision, Project administration, Original Draft Writing, Review and Editing; Zhaoyuan Liu: Project administration, Original Draft Writing, Review and Editing; Nan An, Hao Luo, Conglong Jia, Pengfei Shen, Shihang Jiang, Yingzhe Hu, Yuanhao Gou, Wu Wang, Zhiyuan Feng, Guodong Liu, Xingyu Zhao, Kok Yue Chan, Zilin Su, Zhe Chuan Tan and Guanyang Liu: Simulations and Original Draft Writing; Zeguang Li, Ganglin Yu, Jiyang Yu, and Shanfang Huang: Supervision, Project administration and Review.

References

  1. D.A. Arostegui, M. Holt, Advanced Nuclear Reactors: Technology Overview and Current Issues, Congressional Research Service Report for Congress, Washington, DC, Report, R45706, 2019 [Google Scholar]
  2. M.K. Rowinski, T.J. White, J. Zhao, Renewable Sustainable Energy Rev. 44, 643 (2015) [CrossRef] [Google Scholar]
  3. Y. Guo, Z. Li, K. Wang, Z. Su, Sci. China Technol. Sci. 65, 102 (2022) [Google Scholar]
  4. K. Wang et al., Prog. Nucl. Energy 98, 301 (2017) [CrossRef] [Google Scholar]
  5. P.K. Romano, N.E. Horelik, B.R. Herman, A.G. Nelson, B. Forget, K. Smith, Ann. Nucl. Energy 82, 90 (2015) [CrossRef] [Google Scholar]
  6. L. Deng et al., Nucl. Sci. Tech. 33, 108 (2022) [CrossRef] [Google Scholar]
  7. K. Wang, Ann. Nucl. Energy 82, 121 (2015) [CrossRef] [Google Scholar]
  8. K. Wang et al., RMC-A Monte Carlo Code for Reactor Core Analysis, in SNA+ MC 2013-Joint International Conference on Supercomputing in Nuclear Applications+ Monte Carlo (EDP Sciences, Paris, France, 2013), p. 06020 [Google Scholar]
  9. H. Du, P. Lu, S.C. Liu, Y. Qin, Y. Yan, Y. Sun, Y. Chen, S. Liu, Fusion Eng. Des. 144, 57 (2019) [CrossRef] [Google Scholar]
  10. N. Sun, S. Liu, Z. Wang, P. Shen, Z. Li, K. Wang, Y. Chen, Fusion Eng. Des. 195, 113965 (2023) [CrossRef] [Google Scholar]
  11. N.R. Brown, J. Nucl. Mater. 534, 152139 (2020) [CrossRef] [Google Scholar]
  12. S. Liu, D. She, J.G. Liang, K. Wang, Ann. Nucl. Energy 85, 903 (2015) [CrossRef] [Google Scholar]
  13. Z. Feng, N. An, K. Wang, An Improved Distinct Element Method for High Packing Fraction Stochastic Media Modeling, in EPJ Web of Conferences (EDP Sciences, Cambridge, UK, 2021), Vol. 247, p. 04026 [CrossRef] [EDP Sciences] [Google Scholar]
  14. Z.C. Tan, Z.Y. Feng, K. Wang, Ann. Nucl. Energy 201, 110439 (2024) [CrossRef] [Google Scholar]
  15. Z.C. Tan, Z.Y. Feng, K. Wang, An iterative RSA-DEM method for high packing fraction stochastic media, in Proc. PHYSOR 2024, San Francisco, USA (2024) [Google Scholar]
  16. Z. Feng, N. An, J. Liang, K. Wang, Ann. Nucl. Energy 166, 108821 (2022) [CrossRef] [Google Scholar]
  17. F.B. Brown, D. Griesheimer, W.R. Martin, in Proceedings of the Physics of Fuel Cycles and Advanced Nuclear Systems: Global Developments, Chicago, illinois, April (2004), p. 25 [Google Scholar]
  18. Z. Li, K. Wang, X. Zhang, Research on applying neutron transport Monte Carlo method in materials with continuously varying cross sections, in Proc. ANS Mathematics & Computation Topical Meeting, Nice, France (2011) [Google Scholar]
  19. F.B. Brown, W.R. Martin, Direct sampling of Monte Carlo flight paths in media with continuously varying cross-sections, in Proc. ANS Mathematics & Computation Topical Meeting (2003), Vol. 2 [Google Scholar]
  20. N. An, C. Jia, L. Hao, K. Wang, The Three-Dimensional Continuously Varying Material Transport Method Based on RMC Code, in Proceedings of the Reactor Physics Asia 2023 Conference (2023) [Google Scholar]
  21. P.P. Wilson, T.J. Tautges, J.A. Kraftcheck, B.M. Smith, D.L. Henderson, Fusion Eng. Des. 85, 1759 (2010) [CrossRef] [Google Scholar]
  22. P. Shen, J. Liang, S. Liu, K. Wang, Implementation and Verification of the DAGMC Module in Monte Carlo Code RMC, in International Conference on Nuclear Engineering (American Society of Mechanical Engineers, Shenzhen, China, 2022), Vol. 86366, p. V002T02A075 [Google Scholar]
  23. W. Liu et al., Plasma Sci. Technol. 25, 015103 (2022) [Google Scholar]
  24. W. Wang, K. Li, Y. Guo, C. Jia, Z. Li, K. Wang, Nucl. Eng. Technol. 55, 4685 (2023) [CrossRef] [Google Scholar]
  25. Z. Feng, C. Jia, S. Huang, N. An, K. Wang, Ann. Nucl. Energy 174, 109161 (2022) [CrossRef] [Google Scholar]
  26. D. She, K. Wang, G. Yu, Nucl. Eng. Des. 258, 235 (2013) [CrossRef] [Google Scholar]
  27. D. She, Y. Liu, K. Wang, G. Yu, B. Forget, P.K. Romano, K. Smith, Ann. Nucl. Energy 51, 289 (2013) [CrossRef] [Google Scholar]
  28. W. Li, G. Yu, K. Wang, Ann. Nucl. Energy 137, 107024 (2020) [CrossRef] [Google Scholar]
  29. Y. Qiu, X. Shang, X. Tang, J. Liang, K. Wang, Ann. Nucl. Energy 87, 228 (2016) [CrossRef] [Google Scholar]
  30. G. Shi, C. Jia, X. Guo, K. Li, K. Wang, S. Huang, Q. Cheng, Prog. Nucl. Energy 134, 103643 (2021) [CrossRef] [Google Scholar]
  31. G. Shi, Y. Guo, C. Jia, Z. Feng, K. Wang, S. Huang, Q. Cheng, Ann. Nucl. Energy 154, 108099 (2021) [CrossRef] [Google Scholar]
  32. D.G. Cacuci, Handbook of Nuclear Engineering: Vol. 1: Nuclear Engineering Fundamentals; Vol. 2: Reactor Design; Vol. 3: Reactor Analysis; Vol. 4: Reactors of Generations III and IV; Vol. 5: Fuel Cycles, Decommissioning, Waste Disposal and Safeguards (Springer Science & Business Media, New York, USA, 2010), Vol. 1 [Google Scholar]
  33. H. Li, G. Yu, S. Huang, M. Zhou, G. Shi, K. Wang, Nucl. Sci. Eng. 193, 1186 (2019) [CrossRef] [Google Scholar]
  34. H.M. Dalle, Monte Carlo burnup simulation of the Takahama-3 benchmark experiment, in 2009 International Nuclear Atlantic Conference (2009) [Google Scholar]
  35. H. Li, G. Yu, S. Huang, K. Wang, Ann. Nucl. Energy 159, 108329 (2021) [CrossRef] [Google Scholar]
  36. C. Jia, L. Jian, X. Guo, K. Wang, S. Huang, J. Liang, Ann. Nucl. Energy 173, 109110 (2022) [CrossRef] [Google Scholar]
  37. X. Guo, X. Shang, J. Song, G. Shi, S. Huang, K. Wang, Ann. Nucl. Energy 151, 107864 (2021) [CrossRef] [Google Scholar]
  38. H. Luo, K. Li, N. An, S. Huang, K. Wang, Nucl. Sci. Eng. 1 (2024) [CrossRef] [Google Scholar]
  39. D. Muir, R. Boicourt, A. Kahler, Los Alamos (USA, Los Alamos National Laboratory, 2012) [Google Scholar]
  40. H. Luo, S. Huang, K. Wang, X. Xiao, Comput. Phys. Commun. 294, 108935 (2024) [CrossRef] [Google Scholar]
  41. X. Wang, Y. Liu, W. Martin, K.S. Kim, in Proc. PHYSOR 2018 (2018), pp. 22–26 [Google Scholar]
  42. R. Tuominen, V. Valtavirta, J. Leppänen, Ann. Nucl. Energy 129, 224 (2019) [CrossRef] [Google Scholar]
  43. Q. Pan, J. Rao, S. Huang, K. Wang, Ann. Nucl. Energy 137, 107113 (2020) [CrossRef] [Google Scholar]
  44. Q. Pan, K. Wang, Ann. Nucl. Energy 128, 171 (2019) [CrossRef] [Google Scholar]
  45. M.S. Krick, H.O. Menlove, Tech. rep., Los Alamos Scientific Lab., 1979 [Google Scholar]
  46. B.L. Beers, V.W. Pine, IEEE Trans. Nucl. Sci. 23, 1850 (1976) [CrossRef] [Google Scholar]
  47. D.P. Griesheimer, W.R. Martin, J.P. Holloway, J. Comput. Phys. 211, 129 (2006) [CrossRef] [Google Scholar]
  48. B. Ebiwonjumi, H. Lee, P. Zhang, D. Lee, Functional expansion tallies in Monte Carlo high fidelity LWR analysis, in Proceedings of the Reactor Physics Asia 2019 (RPHA19) Conference (2019) [Google Scholar]
  49. M. Abramowitz, I.A. Stegun, in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (US Government printing office, 1948), Vol. 55 [Google Scholar]
  50. N. An, Q. Pan, X. Guo, S. Huang, K. Wang, Nucl. Eng. Des. 391, 111736 (2022) [CrossRef] [Google Scholar]
  51. H.J. Shim, C.H. Kim, Nucl. Sci. Eng. 157, 132 (2007) [CrossRef] [Google Scholar]
  52. T. Ueki, Nucl. Sci. Eng. 163, 99 (2009) [CrossRef] [Google Scholar]
  53. N. An, X. Guo, T. Huang, K. Wang, A Monte Carlo source convergence diagnosis method based on functional expansion tallies, in Proceedings of the 2023 International Conference on Mathematics and Computation (2023) [Google Scholar]
  54. M.S. Ellis, Ph.D. thesis, Massachusetts Institute of Technology, 2017 [Google Scholar]
  55. A. Novak, P. Romano, B. Wendt, R. Rahaman, E. Merzari, L. Kerby, C. Permann, R. Martineau, R.N. Slaybaugh, Preliminary coupling of OpenMC and Nek5000 within the MOOSE framework, in Proceedings of PHYSOR (2018), Vol. 4 [Google Scholar]
  56. P. Shen, S. Jiang, Y. Hu, K. Wang, Research on the correlations of fission source distribution in the Monte Carlo algorithm using mathematical tools, in International Conference on Nuclear Engineering, Proceedings, ICONE (Virtual, Online, 2022), Vol. 2 [Google Scholar]
  57. P. Shen, X. Huo, Z. Li, Z. Shao, H. Yang, P. Zhang, K. Wang, Nucl. Sci. Tech. 34, 14 (2023) [CrossRef] [Google Scholar]
  58. P. Shen, X. Huo, S. Huang, Y. Guo, Z. Shao, H. Yang, K. Wang, Ann. Nucl. Energy 180, 109468 (2023) [CrossRef] [Google Scholar]
  59. J. Yu, S. Wang, B. Jia, Prog. Nucl. Energy 49, 334 (2007) [CrossRef] [Google Scholar]
  60. H. Luo, N. An, J. Yu, S. Huang, K. Wang, Development of a Neutronics and Thermal-Hydraulics Coupling System with RMC and SUBCHAN, in Proceedings of the Reactor Physics Asia 2023 (RPHA2023) Conference (2023) [Google Scholar]
  61. Y. Guo, Z. Li, S. Huang, M. Liu, K. Wang, Prog. Nucl. Energy 139, 103842 (2021) [CrossRef] [Google Scholar]
  62. Y. Guo, Z. Su, Z. Li, K. Wang, X. Liu, Front. Energy Res. 10, 848799 (2022) [CrossRef] [Google Scholar]
  63. Y. Guo, X. Guo, S. Guo, H. Jiang, Z. Su, G. Wang, Z. Li, K. Wang, D. Qian, J. Yu, Nucl. Eng. Des. 413, 112558 (2023) [CrossRef] [Google Scholar]
  64. D. Poston, M. Gibson, P.R. Mcclure, Proceedings NETS-2018, ANS (2018) [Google Scholar]
  65. P.R. Mcclure, D.I. Poston, S.D. Clement, L. Restrepo, M. Negrete, Nucl. Tech. 206, 43 (2020) [Google Scholar]

Cite this article as: Kan Wang, Zhaoyuan Liu, Nan An, Hao Luo, Conglong Jia, Pengfei Shen, Shihang Jiang, Yingzhe Hu, Yuanhao Gou, Wu Wang, Zhiyuan Feng, Guodong Liu, Xingyu Zhao, Kok Yue Chan, Zilin Su, Zhe Chuan Tan, Guanyang Liu, Zeguang Li, Ganglin Yu, Jiyang Yu, Shanfang Huang. The reactor Monte Carlo code RMC: The state-of-the-art technologies, advancements, applications, and next, EPJ Nuclear Sci. Technol. 10, 24 (2024)

All Tables

Table 1.

Energy deposition in different materials for VERA2G in MeVs.

In the text
Table 2.

Neutron Multiplicity Countings Results (with the mass of 695.04 g of 240Pu).

In the text

All Figures

thumbnail Fig. 1.

Octree-Based Acceleration in RSA (left) and simplified algorithm illustration of the Iterative RSA-DEM Method (right).
In the text
thumbnail Fig. 2.

Illustration of the mixed-transport method in uniform and continuously-varying materials.
In the text
thumbnail Fig. 3.

Radial diagram and simulation results of continuous material distribution of test fuel rod.
In the text
thumbnail Fig. 4.

CAD-based models for neutron transport simulations using RMC. (a) Heat Pipe Reactor (HPR), (b) Sino-UNIted Spherical Tokamak (SUNIST-2).
In the text
thumbnail Fig. 5.

The SF96 lattice benchmark model (left) and power distribution and uncertainty computed using RMC (right).
In the text
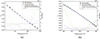thumbnail Fig. 6.

Comparison of the predicted fuel temperature reactivities using perturbation coefficients and the directly calculated results. (a) PWR fuel (T at 900 K), (b) HPR fuel (T at 1000 K).
In the text
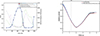thumbnail Fig. 7.

Comparison of transient simulation results in weak (left) and strong (right) neutron fields.
In the text
thumbnail Fig. 8.

Comparison of the normalized energy release energy deposition, and gamma deposition for VERA2G, VERA2P. The color of each cell is determined by the amount of the gamma energy deposition. (a) 2G, (b) 2P.
In the text
thumbnail Fig. 9.

Layout of the HLNC2 model in RMC simulation.
In the text
thumbnail Fig. 10.

Two-dimensional cylinder model.
In the text
thumbnail Fig. 11.

Mesh tally and FET results in contrast.
In the text
thumbnail Fig. 12.

The schematic diagram and initial source distribution and convergent source distribution of the three dimensional source convergence benchmark.
In the text
thumbnail Fig. 13.

FET nuclear thermal-physics coupling flow chart.
In the text
thumbnail Fig. 14.

The FSD SW distance evolution with neutron history [58].
In the text
thumbnail Fig. 15.

Workflow of the file-based coupling in each Picard iteration.
In the text
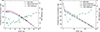thumbnail Fig. 16.

CBC evaluations of BEAVRS cycle 1 (left) and cycle 2 (right).
In the text
thumbnail Fig. 17.

RMC and Fluent models of the micro gas-cooled reactor. (a) RMC model for the core, (b) RMC model for the fuel assembly, (c) 1/8 model using Fluent.
In the text
thumbnail Fig. 18.

The RMC and OpenFOAM model for the KRUSTY reactor.
In the text
thumbnail Fig. 19.

Reactivity and relative power variation (left) and temperature distribution (right) during the transient process.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.