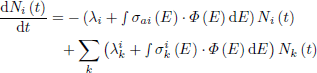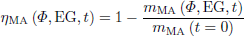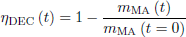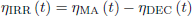| Issue |
EPJ Nuclear Sci. Technol.
Volume 9, 2023
|
|
|---|---|---|
| Article Number | 36 | |
| Number of page(s) | 10 | |
| DOI | https://doi.org/10.1051/epjn/2023021 | |
| Published online | 19 December 2023 | |
https://doi.org/10.1051/epjn/2023021
Regular Article
Multi-group analysis of Minor Actinides transmutation in a Fusion Hybrid Reactor
1
Dipartimento di Ingegneria Industriale, Elettronica e Meccanica, Università degli Studi Roma Tre, Via Vito Volterra 62, 00146 Roma, Italy
2
ENEA-Dipartimento FSN, Via Enrico Fermi 45, 00044 Frascati, RM, Italy
3
GeNERG, DIME, Università di Genova, Via All’Opera Pia, 15, 16145 Genova, Italy
4
INFN, Sezione di Genova, Via Dodecaneso, 33, 16146 Genova, Italy
* e-mail: stefano.murgo@uniroma3.it
Received:
16
June
2023
Received in final form:
10
October
2023
Accepted:
16
November
2023
Published online: 19 December 2023
New nuclear technologies are currently being study to face High Level Waste treatment and disposal issues. Generally, GEN-IV fission Fast Reactors (FR) are considered the waste-burners of the future. In fact, a fast flux turns out to be the best choice for actinides irradiation in critical reactors because of favorable cross section conditions. Differently, Fusion Fission Hybrid Reactors (FFHR) are futuristic devices based on the combination of fusion and fission systems and could represent an alternative to FRs. In such systems, the choice spectrum of the neutron flux that irradiates HLW may be non-obvious due to some operational constraints which have to be considered. To design and optimize these systems as waste-burners, one should fully understand the transmutation dynamics occurring into the fission region. A multi-energy-group analysis by FISPACT-II code has been set to analyze the conversion processes in scenarios characterized by different neutron energy spectra and fluences. The results of this study show that, despite fast fluxes are characterized by better behaviors in terms of radiotoxicity treatment, the difficulties of reaching high reaction yields may require solutions involving moderators or broadened neutron fluxes to increase the reactions probabilities and, consequently, actinides mass conversion yield.
© S. Murgo et al., Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The path to the sustainable development of world economy is one of the hardest challenges of our times. Global institutions and governments are advocating and funding decarbonization activities. The EU aim to be climate-neutral by 2050 is a case in point. This objective is at the heart of the European Green Deal and in line with the EU’s commitment to global climate action under the Paris Agreement [1].
Nuclear power could play a key role in the decarbonization process, being one of the main CO2-free available alternatives to fossil fuels. IEA and IPCC reports [2, 3] state the importance of nuclear energy in future energy mix and EU included it as a transitional activity in the new EU taxonomy [4]. Specifically, this last political act sets conditions on nuclear energy acceptance such as the development of advanced technologies and the construction of waste disposals.
The long-term solution designed for HLW is their storage in permanent disposals, but only a few countries have already built such infrastructures. Reprocessing based on partitioning and transmutation (P&T) processes could help reducing the total size of permanent disposals by recycling a relevant fraction of spent nuclear fuel, transforming a problem in an asset [5].
Spent fuel P&T could be a breakthrough factor in nuclear power revival and should be a main feature of advanced nuclear reactors [6, 7]. Looking at waste recycle as the core business means a radical change in nuclear reactors design. The value of this point of view may lie on the cost reduction of waste management and disposals, the public acceptance of nuclear power, the safety advantages, the increasing of nuclear fuel resources.
Usually, Gen-IV fast Fission Reactors (FR) [8] are considered the nuclear waste convertors of the future. In fact, several analysis state that a fast neutron flux is the best option for actinides conversion (both Pu and Minor Actinides, MA) in power generation reactors since, for high neutron energies, fission tends to prevail on capture and actinides could be conveniently converted to fission products [9–11].
An alternative to FRs could be represented by Fusion-Fission Hybrid Reactors (FFHR) [12], concepts based on the combination of fusion and fission systems. FFHRs could be briefly described as sub-critical fission reactors driven by neutrons produced in reactions occurring in the fusion core.
An FFHR can be designed for power production, waste transmutation, tritium breeding and nuclear fuel production. It could have attractive characteristics:
-
Fission blanket is sub-critical. This aspect makes the system safer than a conventional reactor since criticality accidents cannot occur.
-
It could use a broad range of nuclear fuels (enriched uranium, nuclear waste, natural uranium, and depleted uranium).
-
The design of the fission blanket could be very flexible due to the sub-critical conditions.
Since FFHRs are characterized by limited neutron fluence, the choice of the neutron flux spectrum inside the fission blanket is not obvious due to the consequently impossibility of reaching high reactions yields. To optimize the actinides conversion capability of the fission blanket of an FFHR, it is crucial to know what the transmutation dynamics into the fission blanket are and how they depend on neutron flux (spectrum and intensity) and fluence.
A burn up analysis was set to study the time evolution of a sample of HLW subjected to different neutron flux spectrum scenarios. The aim of this work is to get a preliminary evaluation of FFHR’s waste recycle potential and derive useful indications on their neutronic design. The set irradiation parameters (irradiation time, neutron flux intensity) are those considered suitable for a FFHR that may be built soon, based upon available nuclear technologies.
2. Model
In his 1979 article [12], Bethe suggested the possibility of FFHRs involvement in nuclear systems as a source of enriched fuel for satellite Pressurized Water Reactors (PWR). In Bethe’s scenario, the energy balance of the nuclear system is positive even for fusion reactor 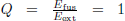 (where Efus is the energy released by the fusion reactor and Eext is the external energy that it needs to operate) since the energy produced by the satellite PWRs must be taken into account.
(where Efus is the energy released by the fusion reactor and Eext is the external energy that it needs to operate) since the energy produced by the satellite PWRs must be taken into account.
The possibility of involving FFHRs in nuclear waste transmutation is under studying. Following Bethe idea, it is possible to imagine an FFHR that serves satellite PWRs as nuclear waste burner/recycler. One of the main advantages of a subcritical reactor is that it could contain big amounts of MA and Pu isotopes without having prompt criticality issues linked to the smaller fraction of delayed neutrons. This cannot be done in critical reactors such as PWR or FR [13].
A fast neutron flux is generally considered the best choice for actinides burning because fission reactions tend to prevail on captures and waste are conveniently converted to fission products. Figure 1 shows the ratios between the fission and capture cross sections in a six groups energy discretization model (energy group structure in Tab. 1) for various isotopes. Data were obtained by processing cross section libraries (ENDF VII, [14]) with the software NJOY21 [15]. When the ratio is higher than 1 the fission reactions prevail. For MA, it happens only for very fast fluxes (EG = 5–6). In the case of Pu isotopes, this condition is reached even for lower energies. Nonetheless, the ratio is somewhat proportional to energy. Obviously, in the case of Pu-239 the ratio is always higher than 1 since it is a fissile isotope.
 |
Fig. 1. Fission vs. capture cross reaction ratios for the main MA and Plutonium isotopes for each energy group. |
Energy group structure.
List of fusion systems.
This paper refers to a hypothetical FFHR which can be described as a subcritical fission reactor powered by an external neutron source obtained by a fusion reactor. The scheme of neutron production is roughly the following:
-
1.
Neutrons are generated by Deuterium-Tritium reactions (D + T => n(14.1 MeV) + α).
-
2.
Neutrons lose some of their energies (or get lost) passing through structural materials.
-
3.
Neutrons enter inside the fission blanket where they induce fission reactions (or get lost). Depending on the fission blanket technology, neutrons can be moderated or not.
A possible neutron source design can be inspired by [23].
Neutron flux amplitude inside the blanket of a FFHR depends mainly on two points:
-
The available neutron source from fusion (Sext).
-
The subcritical multiplication factor M = 1/(1 − keff), where keff is the neutron multiplication factor which represents the ratio between the number of neutrons in two consecutive generations. The reactor is subcritical when k < 1. In this case, in presence of an external neutron source, the reactor’s power output reaches a plateau after a characteristic time.
This implies that the achievable neutron flux is limited with respect to the critical reactors which are typically regarded in literature as waste-burners [6]. Moreover, fusion systems are usually characterized by pulsed operation which reduces the net irradiation time in a substantial manner. Therefore, there is a design optimization substantial problem: since FFHRs are characterized by limited neutron fluence, the choice of the neutron flux spectrum inside the fission blanket could be open to debate because of the impossibility of achieving high fast neutrons reactions yields.
As an example, let’s suppose that keff is 0.97, that the neutron flux on the first wall of the fusion device is 5 ⋅ 1012 n cm−2 s−1 and that no neutron is lost during the path to the fission blanket. Then the neutron flux inside the blanket is of the order of 1.7 ⋅ 1014 n cm−2 s−1 (while fast critical reactors can have fluxes of the order of 1015 n cm−2 s−1). The neutrons generated inside the blanket are fission neutrons with a mean energy of 2 MeV. The result is that the neutron flux is amplified but neutrons energy is substantially modified, and the 14 MeV fusion neutrons represent only a small fraction of the total (less than 5%).
Tables 2 and 3 are a non-exhaustive summary of available alternatives in the field of nuclear fusion and fission technologies. For a Pulsed machine, the Duty-Cycle factor is defined as the ratio between operation and cooling time intervals.
List of fission systems.
Tokamaks have the best plasma confinement properties among fusion reactors and have been selected to be the technologies of international projects ITER [16] and DEMO [17]. RFPs [18] are characterized by features that make them interesting as FFHR fusion systems: ignition could be achievable by ohmic heating only, avoiding the use of additional heating systems; the configuration is not prone to disruption; in principle, the need of a divertor may be avoided, so further simplifying the machine design. However, a price has to be paid in terms of a partly chaotic character of the magnetic field leading to a poorer plasma confinement with respect to Tokamaks, so the path of RFPs towards pure fusion is more difficult.
A transmutation analysis was set to study MA conversion properties of FFHR, defining a sample/target (see Sect. 3) containing only MA and computing the isotopic evolution driven by neutron irradiation with a multi-group approach. Each simulation scenario is characterized by a mono-group neutron flux and a determined neutron flux/fluence, setting some limits to frame the FFHR design problem. With an analysis of this type, it is possible to estimate the dynamic of the transmutation processes and obtain indications on the fission blanket design.
The code FISPACT-II [19] has been used to compute the isotopic evolution of the target. It solves a set of equations called Generalized Bateman Equations. These are balance equations between decay-chains and neutron-nuclei reactions (such as captures, fissions and neutron multiplications). They are defined as:
where N is the mass (or density) concentration of an isotope, λ is a decay constant, σ is a cross section, Φ is the neutron flux. The index i indicates the analyzed isotope while index k indicates its father isotopes.
When energy spectrum is discretized, the integrals in (1) become sums.
FISPACT-II needs the following inputs to operate:
-
A nuclear data library.
-
A neutron flux (spectrum and intensity).
-
The definition of an irradiation cycle.
-
A sample.
The nuclear data library used in the computations is the TENDL 2017 [20]. This library was suggested in FISPACT-II examples, and it was considered appropriate for this study.
The nuclear flux and irradiation cycle are chosen as follows. A multigroup model was set to estimate the sensitivity of a MA target transmutation to different neutron spectra. Table 1 shows the energy group structure (Number of groups, NG; Energy Group number, EGn). The neutron flux intensity was set to 1013, 1014 and 1015 n cm−2 s−1 (Number of set intensities, NI = 3) and the maximum net irradiation time was set to 15 years, assuming the maximum duty cycle of the fusion machine as 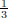 of the operation time and the lifespan of the system as 45 years. The neutron fluence (F) is obtained by multiplying the flux and the irradiation time and it is in the range 0 − 5 ⋅ 1023 n cm−2.
of the operation time and the lifespan of the system as 45 years. The neutron fluence (F) is obtained by multiplying the flux and the irradiation time and it is in the range 0 − 5 ⋅ 1023 n cm−2.
The sample used in computations was a target of minor actinides (Neptunium, Americium and Curium) as described in Section 3.
Then NG × NI computations were run, using each time a different mono-group neutron flux input varying the energy group EG and the intensity Φ. To simplify calculations, the irradiation was set as continuous, instead of pulsed.
It is then possible to analyze the effects of different neutron fluxes (in terms of energy spectrum and intensity) on the transmutation target. Results show time evolution of MA, U and Pu masses and radiotoxicity, here quantified via the ingestion dose.
The computing resources and the related technical support used for this work have been provided by CRESCO/ENEAGRID High Performance Computing infrastructure and its staff [21]. CRESCO/ENEAGRID High Performance Computing infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by Italian and European research programmes, see http://www.cresco.enea.it/english for information.
3. Target/sample description
A target actinides sample (Total mass = 1 kg) has been considered whose composition (shown in Tab. 4) was derived from the isotope concentration measurements on the spent fuel of Neckarwestheim Nuclear Power Station module 2 (GKN 2, Neckarwestheim, Germany) [22]. MA represent about the 0.15% of total initial fuel mass as 1 kg of MA derives from an initial enriched Uranium mass of about 653 kg. The relative masses of actinides isotopes were extrapolated from GKN spent fuel to elaborate the composition of the target. This can be seen as part of a heterogeneous blanket, i.e., a core which is composed by fuel rods and targets located in defined locations. This configuration analysis fits good with this core configuration because Minor Actinides are considered just as passively irradiated elements.
Isotopic composition of the target.
As an estimate, for a typical PWR fresh fuel input (≈100 tonnes of U, irradiation time ≈18–24 months), MA production rate is of the order of 50–100 kg/year.
The main isotopes included in the sample composition are Np-237, Am-241, Am-243, Cm-244 which represent respectively about the 40%, 35%, 16% and 8.7% of the target mass.
4. Results
Results obtained by FISPACT-II outputs elaboration are shown in the following. FISPACT-II gives results for all the elements generated during the irradiation process. Results are shown only for U, Np, Pu, Am, Cm and fission products since they represent most of the target mass at each time step.
4.1. Minor Actinides mass conversion
A function called Minor Actinides Conversion Efficiency was defined as:
In this case, “conversion” means the transmutation of MA isotopes to U and Pu isotopes or fission products (FP).
In the context of this analysis, it is interesting to separate the effects of irradiation and decay on the conversion efficiency to estimate the effect of recycle with respect to the conversion (decay) that could be obtained simply by a disposal approach. Computed ηMA were thus corrected eliminating the contribution of decay. To do so, a function called ηDEC (3) was defined and subtracted from each 15-year irradiation scenario results.
Reference to the corrected ηMA function will be made as ηIRR (4). It was then possible to write ηIRR as a function of neutron fluence by merging the results of each simulation.
Figure 2 a shows the evolution of corrected ηIRR as a function of neutron fluence for each mono-group neutron flux input while Figure 2b shows the time evolution of ηDEC.
 |
Fig. 2. a) Results without the effect of pure decay (filtered data); b) Conversion efficiency of pure decay on the actinide target. |
The fact that plots in Figure 2 are smooth suggests that, as a first estimate, same fluences give same conversion results, no matter the flux intensity. This is a very helpful feature because producing data as functions of fluence is easier (for example, we would have needed NG runs instead of NI × NG runs to obtain similar results). Moreover, neutron fluence is a more comprehensive function than neutron flux which makes it more interesting in this kind of analysis.
EG 1-2 curves exhibit a maximum. This is an important result since the time at which the maximum of the conversion efficiency is reached can be interpreted as the discharge time of the target. One of the differences between a heterogeneous blanket (fuel + waste targets) and a homogeneous one (fuel and waste mix) lays on this point: “waste” (Np, Am, Cm) and fuel (U, Pu) can have different discharge times. In an heterogenous blanket, the separation of fuel and waste accommodates the difference of discharge time; on the other hand, the output of a homogeneous blanket may require a reprocessing cycle to reach maximum conversion efficiencies.
EG 3-4 have a significant role in the mass conversion of actinides isotopes only with high fluences (F ≈ 1023 n cm−2). In particular, EG 3 curve achieves almost the same conversion efficiency as EG 1-2 with the maximum fluence set.
An interesting result is that EG 6 has a higher mass conversion efficiency than EG 5. The reason of such behavior is that fast fissions have high threshold energies which are largely meet in the EG 6. However, the effect on MA mass conversion of the fastest fraction of the neutron spectrum, EG 5-6, has a lower importance even for the maximum fluences set. It slightly differs from the effect of pure decay with fluences of the order of 1023 n cm−2. Moreover, it should be noted that a very fast flux can only arise by neutron fusion source and not by fission multiplication. A fission peak, in fact, mainly corresponds to EG 4 (and partially EG 3-5). Consequently, to have a relevant number of neutrons in EG 5-6, the neutron source from fusions must be very powerful. This could be unfeasible.
To fully understand the conversion processes dynamics, we analyzed the evolution of the target composition. Figure 3a–c shows the composition evolution of the actinides target for the cases: a) EG = 1; b) EG = 3; c) EG = 6, which are representative of the transmutation at different neutron flux energy level. Results are presented as mass content for each element at different neutron fluences (Mirr). Results were obtained with a correction process similar to that described above. Decay contribution was neglected subtracting the mass variation linked to natural depletion at each specific time in order to elucidate the effect of irradiation on isotopes mass consumption/production.
 |
Fig. 3. Isotopes mass evolution with respect to natural decay: a) EG = 1; b) EG = 3; c) EG = 6. Legend: U = Uranium; Np = Neptunium; Pu = Plutonium; Am = Americium; Cm = Curium; FP = Fission products. |
The scenarios exhibit an increase (and decrease, in the the case of EG = 1) in Pu concentration. This is the main effect of the irradiation of MA. In fact, FP represent only a small fraction of the sample even for higher fluences and energies. Moreover, FP appear to derive mostly by Pu isotopes fissions.
EG 1 scenario exhibits an overall reduction of MA isotopes but also an increase in Cm concentration. This last feature is a tricky point: since Cm isotopes are highly radioactive and subjected to spontaneous fission, they could raise issues related to neutron sources in fuel facilities [9]. Specifically, it seems a better option to wait for target irradiation until Cm isotopes are vanished by natural decay (Cm-242, Cm-243 and Cm-244 have low half-lives, see Tab. 4).
Recalling that the target is mainly composed by Np-237, Am-241, Am-243 and Cm-244, it can be noted that:
-
Np-237 is converted to Pu efficiently through the chain Np-237 → Np-238 → Pu-238.
-
Pu isotopes are also obtained by the chains Am-241 → Am-242 → Cm-242 → Pu-238 and Am-243 → Am-244 → Cm-244 → Pu-240.
-
Cm isotopes build up especially for thermal neutron fluxes due to capture reactions predominance on decays.
4.2. Minor Actinides Radiotoxicity treatment
As known, the harm related to the exposure to a radioactive waste can be quantified by means of radiotoxicity. This parameter considers the radioactivity of a certain waste and its (biological and physical) half-life, having the dimension of a dose (Sv). Since its definition is not univocal, the ingestion dose function (computed by FISPACT) was used as reference. The ingestion dose relative to the natural Uranium from which the MA sample (Level Of Mine, LOM) has been computed (Mass of enriched Uranium ≈653 kg, U-235, enrichment = 3.8%, U-235 abundance in the enrichment tail = 0.25%). The intersection between the waste and natural Uranium ingestion dose curves (Level Of Mine Balancing Time, LOMBT) estimates the repository time. Figure 4 shows a comparison among the evolution of the LOMBT as a function of neutron fluence for different neutron spectra. For each case, only the dose contribution of Np, Am and Cm isotopes (and Cf, when needed) were considered and a net irradiation time t = 15 years was set.
 |
Fig. 4. LOMBT as a function of neutron fluence for different neutron spectra irradiation scenarios (t = 15 years). |
From our computation LOMBT related to Pure Decay is about 3480 years. The neutron flux has a positive effect on the repository time, with the exception of EG 2, reducing it by a maximum of about 200 years. The thermal spectrum scenario shows a good behavior for low fluences while scenarios related to faster spectra need higher fluences to reach relevant results.
At higher fluences, the LOMBT (EG = 1) increases mainly because of the build-up of Cm-248 which has a half-life of 3.48 × 105 years. The scenario EG = 2, instead, shows a production of Cf which turns out to increase the repository time at high fluences.
It is interesting to note how LOMBT is influenced by the total mass of actinides contained in the target only partially. Most of the results depend on the toxicity of the nuclear waste produced. For example, EG2 irradiation shows the best results in mass conversion (η up to 0.6) but, at the same time, increases repository time. In general, faster groups scenarios, tends to produce less very-toxic isotopes than thermal and epithermal groups because capture is less-favoured. Therefore, the fraction of high mass number MA, such as Cm-248, Cf-242, after irradiation is lower. This is the reason why, at high fluences, repository time decreases only for EG 3-4-5-6.
One should expect that, increasing fluences, EG 3 and EG 4 irradiation scenarios would show behaviors like those related to low thermal neutron fluences for both mass conversion and LOMBT reduction. In fact, since fission threshold energies for MA are of the order of 1 MeV, captures would be predominant as in EG1. Curves would be somewhat translated and scaled due to different reaction dynamics.
It is interesting to note as well as EG = 6 scenario shows a lower LOMBT than the EG = 5 one at almost the same conversion efficiency. This result may depend on the fact that fission channels are more active in EG 6 irradiation and some of MA mass is converted to fission products.
In the case of EG1 irradiation, the LOMBT reduction at low fluences is probably given by the capture channel Np-237 => Np-238 which is very efficient for thermal groups. So, the increase in toxicity is initially somewhat balanced by Np mass conversion.
5. An example of a realistic neutron spectrum in a FFHR
In general, in a realistic FFHR, MA would be irradiated together with nuclear fuel such as Pu and U isotopes. Moreover, the impossibility of reaching high reaction yields may make it necessary the use of broadened neutron spectra configurations. A good compromise for U, Pu and MA conversion in FFHRs may be the irradiation with a fast neutron flux moderately broadened to guarantee the presence of an (epi)thermal tail in the neutron spectrum. In fact, as explained above, fast neutron systems have a favorable fission vs. capture probabilities ratio and would produce a lower fraction of waste during Pu and U irradiation. This configuration could be possibly achieved by designing a blanket with a relatively light mass number coolant (e.g., Molten Salts or Sodium).
Here the results related to a neutron flux scenario set on a compromise of this kind are presented. Figure 5a–c shows the energy groups definition, irradiation conversion efficiency and LOMBT evolution by fluence for the tested scenario. Energy groups definition is estimated and adjusted on the base of previous studies evaluations [23]. Fusion neutrons (EG6) are set to 5% of the total, that has to be considered as a high limit. In fact, in a FFHR blanket, most of neutrons are emitted by fission reactions and can be moderated or not, depending on the core technology.
 |
Fig. 5. a) Neutron flux energy spectrum for the tested scenario; b) Irradiation conversion efficiency as a function of the neutron flux for the tested scenario; c) LOMBT as a function of fluence for the tested scenario (t = 15 years). |
Results show that it could be possible to convert up to 50% of the actinide sample mass without increasing the waste repository time (and producing new fuel). Moreover, the neutron fluences needed for achieve good conversion results appear to be reasonable even for futuristic FFHR.
Obviously, once a real blanket is defined, this analysis should be completed by comparing these results to those related to waste production by fuel irradiation.
The high safety margins guaranteed by an FFHR enable to consider also more complex configurations. For example, an alternative may be represented by a blanket with thermal regions, filled with MA, similarly to what already proposed in [24]. The feasibility of this last scenario will be investigated in future studies.
6. Discussion and conclusions
Waste disposals design depends on two fundamental parameters: the waste quantity (mass and volume) and its disposal time. An efficient waste treatment via irradiation should give good results in waste mass conversion and disposal time reduction.
The results show that, under certain limitations (Φmax = 1015 n cm−2 s−1, tmax = 15 years), it is possible to achieve high actinide mass conversion efficiencies (up to 60%) only in scenarios related to neutron energies in the range 0–100 keV. The transmutation processes turned out be dominated by capture reactions. Consequently, the main irradiation effect is the conversion of actinides to Pu isotopes (new fuel) and high-mass-number MA.
Irradiation appears to generally reduce the repository time of MA in each tested scenario. The thermal spectrum scenario shows a good behavior for low fluences while scenarios related to faster spectra need higher fluences to reach relevant results.
The design of the FFHR machine will necessarily depend on the maximum neutron fluence that is feasible and on the desired objective, i.e., whether to prefer higher mass conversion or lower repository time. A good compromise for U, Pu and MA conversion in FFHRs may be the irradiation with a fast neutron flux moderately broadened to guarantee the presence of an (epi)thermal tail in the neutron spectrum.
The high safety margins guaranteed by an FFHR enable to consider also more complex configurations. For example, an alternative may be represented by a blanket with moderated regions where actinides may be irradiated separately from the nuclear fuel. The feasibility of this last scenario will be investigated in future studies.
Some other observations must be added to this treatment:
-
Analysis should be completed with a comparison between actinides converted by target irradiation and produced by Pu irradiation.
-
If a thermal blanket is designed, a good choice to avoid Cm and high mass number Am isotopes production could be to separate and irradiate only Np (and Pu).
-
The analysis was set with a continuous (not pulsed) irradiation. This is an approximation that probably overestimate the Cm concentration (Cm-244 half-life is ≈18 years).
-
One of the main issues related to MA irradiation with a thermal flux is the accumulation of Cm. Some limits on its concentration should be set [9].
-
A complete analysis of HLW treatment and disposal issues should involve the production of lower-level waste, heat production vs. time and chemical studies [25].
In conclusion, this work gives indications on the transmutation properties of FFHRs. The impossibility of reaching high reaction yields may require solutions involving moderators or broadened neutron fluxes to increase the reactions probabilities. The main effect of neutron irradiation will be in any case the conversion of part of MA in Pu. The main advantages in using a FFHR instead of a FR for waste transmutation targets may lay on the operation safety margins and the possibility of inserting larger quantities of actinides into the blanket. Research and developments on fusion reactors technologies could make FFHR even more interesting with the possibility of achieving high reaction rates in a very fast region of the neutron spectrum (up to 15 MeV), unreachable for FR, enabling an efficient transmutation of HLW and Pu isotopes.
Conflict of interests
The authors declare that they have no competing interests to report.
Funding
This research did not receive any specific funding, but the research activity of Stefano Murgo has been supported by PhD PON (Programma Operativo Nazionale) grant (“Study of Fusion Fission Hybrid System potentiality for nuclear waste transmutation and energy sustainability”) provided by the Italian Ministry of University and Research (MUR). The PhD course is held at Roma Tre University (XXXVII cycle).
Data availability statement
Figure 1 were produced elaborating ENDF-VII cross section data [14] by NJOY21 [15].
The SCALE 5.1 Predictions of PWR Spent Nuclear Fuel Isotopic Compositions dataset [22] contains a lot of data regarding transmutation of PWR spent nuclear fuel. We produced the data in Table 4 elaborating those contained in this reference (GKN 2 section).
TENDL-2017 cross section data [20] were used as FISPACT-II [19] input.
We used MatLab and Microsoft Excel to elaborate FISPACT-II outputs. Results are summarized in Figures 2–5. FISPACT-II outputs and corresponding elaborated data can be available on request.
Author contribution statement
All the authors gave important contributions to the paper. A detailed list of the different performed activities is provided as follows:
– Stefano Murgo: corresponding author, simulations, data elaboration and analysis, activity coordination.
– Marco Ciotti: activity coordination and article revision.
– Guglielmo Lomonaco: data elaboration and analysis, article revision.
– Nicola Pompeo: activity coordination and article revision.
– Fabio Panza: simulations, data elaboration and analysis, activity coordination, article revision.
References
- 2050 long-term strategy, https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2050-long-term-strategy en [Google Scholar]
- IEA, Nuclear Power in a Clean Energy System (IEA, Paris, 2019), https://www.iea.org/reports/nuclear-power-in-a-clean-energy-system [Google Scholar]
- J. Rogelj, D. Shindell, K. Jiang, S. Fifita, P. Foster, V. Ginzburg, C. Handa, H. Kheshgi, S. Kobayashi, E. Kriegler, L. Mundaca, R. Séférian, M.V. Vilariño, in Mitigation Pathways Compatible with 1.5° C in the Context of Sustainable Development (IPCC/WMO, 2018), pp. 93–114. [Google Scholar]
- EU Taxonomy: Commission welcomes the result of today’s vote by the European Parliament on the Complementary Delegated Act, 6th July 2022 [Google Scholar]
- B. Vezzoni et al., Preliminary evaluation of a nuclear scenario involving innovative gas cooled reactors, Sci. Technol. Nucl. Install. 2009, 16 (2009) [CrossRef] [Google Scholar]
- E. Bomboni, N. Cerullo, G. Lomonaco, V. Romanello, A critical review of the recent improvements in minimizing nuclear waste by innovative gas-cooled reactors, Sci. Technol. Nucl. Install. 2008, 18 (2008) [CrossRef] [Google Scholar]
- E. Bomboni, N. Cerullo, G. Lomonaco, Assessment of LWR-HTR-GCFR integrated cycle, Sci. Technol. Nucl. Install. 2009, 14 (2009) [Google Scholar]
- N. Cerullo, G. Lomonaco, Generation IV reactor designs, operation and fuel cycle, Nucl. Fuel Cycle Sci. Eng., Woodhead Publishing Series in Energy 2012, 333 (2012) [CrossRef] [Google Scholar]
- M. Salvatores, G. Palmiotti, Radioactive waste partitioning and transmutation within advanced fuel cycles: Achievements and challenges, Prog. Part. Nucl. Phys. 66, 144 (2011) [CrossRef] [Google Scholar]
- M. Salvatores, Nuclear fuel cycle strategies including Partitioning and Transmutation, Nucl. Eng. Des. 235 805 (2004) [Google Scholar]
- T.A. Taiwo, R.N. Hill, Summary of Generation-IV Transmutation Impacts, Nuclear Engineering Division (Argonne National Laboratory, Argonne, USA, 2005) [CrossRef] [Google Scholar]
- H. Bethe, The fusion hybrid, Phys. Today 32, 44 (1979) [CrossRef] [Google Scholar]
- S. Glasstone, M.C. Edlund, The Elements of Nuclear Reactor Theory (D. Van Nostrand Company, 1952) [Google Scholar]
- ENDF VII, https://www.nndc.bnl.gov/endf-b7.1/index.html [Google Scholar]
- NJOY21, https://www.njoy21.io/NJOY21 [Google Scholar]
- ITER, https://www.iter.org/ [Google Scholar]
- DEMO, https://euro-fusion.org/programme/demo/ [Google Scholar]
- L. Marrelli, P. Martin, M.E. Puiatti, J.S. Sarff, B.E. Chapman, J.R. Drake, D.F. Escande, S. Masamune, The reversed field pinch, Nucl. Fusion 61, 023001 (2021) [CrossRef] [Google Scholar]
- FISPACT-II, https://fispact.ukaea.uk/ [Google Scholar]
- TENDL 2017, https://tendl.web.psi.ch/tendl_2017/tendl2017.html [Google Scholar]
- F. Iannone, et al., CRESCO ENEA HPC clusters: a working example of a multifabric GPFS Spectrum Scale layout, in 2019 International Conference on High Performance Computing & Simulation (HPCS), Dublin, Ireland (2019), pp. 1051–1052 [Google Scholar]
- G. Radulescu, I.C. Gauld, G. Ilas, SCALE 5.1 Predictions of PWR Spent Nuclear Fuel Isotopic Compositions ((Oak Ridge National Laboratory, 2010) [CrossRef] [Google Scholar]
- R. Piovan et al., Pilot Hybrid Experiment with Reversed Field Pinch as neutron source and double test beds: an innovative stage approach towards a full power Fusion-Fission Hybrid Reactor, in Technical Meeting on Synergies between Nuclear Fusion Technology Developments and Advanced Nuclear Fission Technologies (Wien, Austria, 2022) [Google Scholar]
- D. Chersola, G. Lomonaco, R. Marotta, The VHTR and GFR and their use in innovative symbiotic fuel cycles, Prog. Nucl. Energy 83, 443 (2015) [CrossRef] [Google Scholar]
- L.M. Krall, A.M. Macfarlane, R.C. Ewing, Nuclear waste from small modular reactors, PNAS 119, e2111833119 (2022) [CrossRef] [Google Scholar]
Cite this article as: Stefano Murgo, Marco Ciotti, Guglielmo Lomonaco, Nicola Pompeo and Fabio Panza, Multi-group analysis of Minor Actinides transmutation in a Fusion Hybrid Reactor, EPJ Nuclear Sci. Technol. 9, 36 (2023)
All Tables
All Figures
 |
Fig. 1. Fission vs. capture cross reaction ratios for the main MA and Plutonium isotopes for each energy group. |
| In the text | |
 |
Fig. 2. a) Results without the effect of pure decay (filtered data); b) Conversion efficiency of pure decay on the actinide target. |
| In the text | |
 |
Fig. 3. Isotopes mass evolution with respect to natural decay: a) EG = 1; b) EG = 3; c) EG = 6. Legend: U = Uranium; Np = Neptunium; Pu = Plutonium; Am = Americium; Cm = Curium; FP = Fission products. |
| In the text | |
 |
Fig. 4. LOMBT as a function of neutron fluence for different neutron spectra irradiation scenarios (t = 15 years). |
| In the text | |
 |
Fig. 5. a) Neutron flux energy spectrum for the tested scenario; b) Irradiation conversion efficiency as a function of the neutron flux for the tested scenario; c) LOMBT as a function of fluence for the tested scenario (t = 15 years). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.