| Issue |
EPJ Nuclear Sci. Technol.
Volume 1, 2015
|
|
|---|---|---|
| Article Number | 15 | |
| Number of page(s) | 8 | |
| DOI | https://doi.org/10.1051/epjn/e2015-50055-0 | |
| Published online | 11 December 2015 | |
https://doi.org/10.1051/epjn/e2015-50055-0
Regular Article
Sensitivity analysis of minor actinides transmutation to physical and technological parameters
CEA Cadarache, DEN/DER/SPRC/LEDC, Bat. 230, 13108 Saint-Paul-lez-Durance, France
* e-mail: timothee.kooyman@cea.fr
Received:
24
September
2015
Received in final form:
30
October
2015
Accepted:
3
November
2015
Published online:
11
December
2015
Minor actinides transmutation is one of the three main axis defined by the 2006 French law for management of nuclear waste, along with long-term storage and use of a deep geological repository. Transmutation options for critical systems can be divided in two different approaches: (a) homogeneous transmutation, in which minor actinides are mixed with the fuel. This exhibits the drawback of “polluting” the entire fuel cycle with minor actinides and also has an important impact on core reactivity coefficients such as Doppler Effect or sodium void worth for fast reactors when the minor actinides fraction increases above 3 to 5% depending on the core; (b) heterogeneous transmutation, in which minor actinides are inserted into transmutation targets which can be located in the center or in the periphery of the core. This presents the advantage of decoupling the management of the minor actinides from the conventional fuel and not impacting the core reactivity coefficients. In both cases, the design and analyses of potential transmutation systems have been carried out in the frame of Gen IV fast reactor using a “perturbation” approach in which nominal power reactor parameters are modified to accommodate the loading of minor actinides. However, when designing such a transmutation strategy, parameters from all steps of the fuel cycle must be taken into account, such as spent fuel heat load, gamma or neutron sources or fabrication feasibility. Considering a multi-recycling strategy of minor actinides, an analysis of relevant estimators necessary to fully analyze a transmutation strategy has been performed in this work and a sensitivity analysis of these estimators to a broad choice of reactors and fuel cycle parameters has been carried out. No threshold or percolation effects were observed. Saturation of transmutation rate with regards to several parameters has been observed, namely the minor actinides volume fraction and the irradiation time. Estimators of interest that have been derived from this approach include the maximum neutron source and decay heat load acceptable at reprocessing and fabrication steps, which influence among other things the total minor actinides inventory, the overall complexity of the cycle and the size of the geological repository. Based on this analysis, a new methodology to assess transmutation strategies is proposed.
© T. Kooyman and L. Buiron, published by EDP Sciences, 2015
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Minor actinides transmutation represents a potential solution to decrease the amount and hazards caused by nuclear. It can be achieved by subjecting minor actinides nuclei to a neutron flux. Minor actinides transmutation can take two forms, either the minor actinide nuclei undergoes fission and yields fission products which are shorter lived or captures a neutron and is transmuted into another heavy nuclide. The main minor actinides that are produced in nuclear reactors are:
-
237Np, produced by neutron capture on 235U in light-water reactors, decaying to 233Pa with a half-life of 2.14 × 106 years. It is also produced by (n, 2n) reactions on 238U in fast reactors and from 241Am decay;
-
241Am, produced by decay of 241Pu and decaying to 237Np with a half-life of 432 years;
-
243Am, produced by neutron capture on 242Pu and decaying to 239Pu with a half-life of 7370 years;
-
244Cm which is produced by capture on 243Am which decays to 240Pu with a half-life of 18.1 years and which is mainly found in MOX fuels.
When plutonium is recovered from the spent fuel by reprocessing and then reused, only minor actinides and fission products remain in the final waste, along with the small uranium and plutonium losses from the reprocessing step. In this case, both long-term radiotoxicity and final spent fuel repository design constraints are dominated by minor actinides, as the fission products contribution become negligible after a few hundred years.
Minor actinides transmutation consequently appears as a potential strategy to minimize the fraction and mass of MA in the waste and reduce the spent fuel burden. As such, it was included in the 2006 French law on nuclear waste management as a research option to deal with nuclear wastes management. In the asymptotic case of a complete multi-recycling of all minor actinides, the only waste would be the associated reprocessing losses, which can be as low as 0.01% [1] of the reprocessed mass, thus dividing by a factor up to 1000 the impact of minor actinides.
Minor actinides transmutation has been studied for several decades and many concepts have been discussed so far. We will only focus here on transmutation in critical reactors. Studies have been made on transmutation in thermal [2] and fast reactors [3], either in dedicated [4] or industrial reactors with various types of fuel, coolant and minor actinides isotopic vector. Several experiments have also been carried in various reactors such as the SUPERFACT experiment in the PHENIX reactor [5] or more recently the METAPHIX experiments in the same reactor.
Fast reactors exhibit an advantage for transmutation compared to thermal systems as they have a higher neutron excess and as they produce less minor actinides from capture on plutonium isotopes. So far, transmutation options for such reactors can be divided in two different approaches. In the homogeneous approach, minor actinides are loaded in the core in fractions higher than in the natural fraction of minor actinides present in the fuel at equilibrium (below 0.5% depending on the spectrum). For minor actinides content above 2–5%, depending on the core design, reactivity coefficients such as Doppler feedback and coolant void worth are negatively impacted, which has an impact on safety performances of the core (see Refs. [3,6]). If we consider reference core design for sodium cooled reactors, minor actinides fraction in the fuel is limited to 2.5–3% to keep acceptable reactivity coefficients [7].
Additionally, this approach exhibits the drawback of “polluting” the entire fuel cycle with minor actinides, thus increasing the cost of every step of the fuel cycle [8].
In the heterogeneous approach, minor actinides are inserted into transmutation targets which can be located in the center or in the periphery of the core. This presents the advantage of dissociating the management of the minor actinides from the conventional fuel and not impacting the core reactivity coefficients.
A transmutation strategy can have various objectives: the goal can be to limit the minor actinides inventory while operating a nuclear reactor fleet, or to transmute the minor actinides stockpile originating from the current operations of LWRs. The interest of the use of a given reactor type for transmutation purposes must be evaluated bearing in mind this final objective. Preliminary questions such as the use of dedicated reactors and reprocessing facilities must also be solved before designing a complete transmutation strategy.
We considered here that the main goal of transmutation issues was to minimize the volume and burden in terms of repository size and radiotoxicity of the waste associated with nuclear energy. Consequently, we made the hypothesis of a closed cycle with plutonium multi-recycling. Only transmutation in fast reactors spectrum was studied here, as a fast spectrum appears to be more suited to transmutation. The results are detailed here for transmutation in homogeneous mode which shows the best performances but the conclusions are quite similar for transmutation in heterogeneous mode.
2 Scope of the study
Most of the work related to transmutation has been carried out seeking for an efficient transmutation system, that is to say a reactor design which exhibits high minor actinides consumption rate with “acceptable” safety parameters. The common approach to this problem was to start from an existing core and modify it to accommodate the loading of a given fraction of minor actinides, as it is proposed for instance in [9], where the core geometry is modified to decrease the sodium void worth, permitting a subsequent addition of minor actinides in the reactor.
A drawback of this approach is that it focuses solely on the reactor side of the transmutation process while additional constraints on the strategy related to fuel cycle must also be taken into account. Indeed, minor actinides bearing fuels typically lead to complications at the fabrication stage and have more stringent mechanical requirements due to an increased helium production in the fuel. Minor actinides bearing fuel handling and reprocessing are also more complicated, due to their important decay heat and neutron source. Consequently, they also require enhanced radioprotection shielding during the fabrication process.
The aim of this work was to implement a low-level approach to the transmutation concept. First, a global study of the reactor parameters which may have an impact on transmutation has been carried out. Then, fuel cycle considerations and constraints were taken into account to evaluate their effect both on transmutation and on the reactor parameters. From the results, it was then possible to identify a set of relevant parameters which encompassed both reactor and fuel cycle constraints and to outline a global methodology for the design of a comprehensive transmutation strategy.
3 Methodology
A simplified approach of reactor physics was used to evaluate the impact of various parameters on transmutation performances. In order to assess their effect on fuel cycle aspects, a simplified equilibrium algorithm described in Figure 1 was used. The list of parameters which were studied for the reactor part is given in Table 1. The plutonium fraction in the fuel is set at 20%.
A moderating material was added to the cell in some cases to evaluate the effect of a degraded spectrum, even in unrealistic quantities. Even if this material is denominated “moderator” in this paper for simplicity of language, it was not added in the medium as a design feature but as solution to explore a wide range of potentially available spectrum. Variation ranges of the various materials were voluntarily taken as extreme in order to correctly evaluate all possible configurations. As such and due to the simplicity of the model considered, the results cannot be directly transposed to reach a conclusion regarding full-core model. For instance, a full-core model would incorporate information about the geometrical design of the assembly, which feasibility depends on the fuel/coolant/moderator chosen for instance. However, the model used is enough to give a broad understanding of the effects of neutron spectrum variation and broad design parameters such as fuel or coolant fraction in the core, or power.
To simulate the irradiation, 33 group cross-sections were calculated using a homogeneous cell model and the ECCO cell code [10]. These cross-sections were then collapsed into one group cross-sections for depletion calculation which were carried out with a constant flux and a depletion chain ranging from 234U to 252Cf. Cooling down was simulated using the same depletion calculation without flux. Minimal cooling time was set at 5 years and no limits were considered for upper cooling time. The effect of the following parameters was studied:
-
maximum allowable decay heat at reprocessing;
-
maximum allowable neutron source at reprocessing;
-
manufacturing time.
The impact of each parameter on the transmutation performances was estimated using the transmutation rate, defined as the fraction of a nuclide having disappeared either by capture or by fission, and the fission rate, which is the ratio of nuclides which have undergone fission over the number of nuclides having disappeared.

The core was initially loaded with a given volume fraction of minor actinide with the vector given in Table 2. This vector is deemed representative of what should be available in France by 2035. The mass of fuel which had undergone fission was replaced with the equivalent mass of initial feed to keep a constant mass of fuel. The algorithm was stopped once the difference between the 241Am fraction in the fuel at the beginning of two consecutive cycles was below 0.5%.
It has to be noted here that for several nuclides, the main one being 241Am, the transmutation rate can be defined either between the beginning and the end of irradiation or between the start of irradiation and the end of reprocessing, as there will be a production of 241Am during reprocessing due to 241Pu decay. We referred to the first one as the “irradiation transmutation rate” and the second one as the “cycle transmutation rate”.
For decay heat calculations, the isotopes used are given in Table 3. Fission products contribution to the total residual power was neglected, as their contribution to the residual power is only 10% after 5 years cooling for MOX fuels irradiated in fast reactors, which is the minimal delay which was considered. The power density was calculated for an assembly of 175 kg of heavy nuclides.
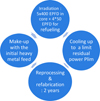 |
Fig. 1 Algorithm used for multi-recycling simulation. |
Reactor parameters.
Minor actinides isotopic vector.
Isotopes used for residual power calculations and neutron source calculations.
4 Results from reactor analysis
The impact of each parameter discussed in Table 1 on the fission rate and the transmutation was assessed in order to pinpoint the relevant ones. Representative volume fractions of a typical fast reactor were taken with 40% of fuel, 40% of coolant and 20% of structures.
4.1 Effect of the fuel type and fraction
The decrease in the transmutation rate concomitant with the increase in the fission rate when going from oxide to metal, as seen in Table 4, is explained by the modification of the spectrum in the cell. With a metal alloy fuel, the harder spectrum leads to a lower capture cross-section for the minor actinides, which decreases the total absorption cross-section and thus the transmutation rate while increasing the fraction of fissions for the same irradiation time of 1000 EPFD.
One can note that the range of variations of both rates is limited to a few percent, which leads to the conclusion that the choice of the fuel will be mainly dictated by thermo-mechanical constraints pertaining to the residence time, flux level and reactor technology rather than by solely neutronic considerations. The increase of the fuel fraction slightly hardens the spectrum thus slightly decreases transmutation rate by a few percent.
Effect of the fuel type for a cell with 6.5% Am, averaged over the results for the three coolant types.
4.2 Effect of the coolant type and fraction
Similarly to the previous case, we can observe in Table 5 here that a small change in the spectrum due to the use of a lighter or heavier coolant has a small effect on the fission and transmutation rate, but once again, this is limited to a few percent so it is concluded that coolant choice will more likely be driven by safety constraints and technological considerations rather than by neutronic aspects.
Effect of the coolant material type for a cell with 6.5% Am, averaged over the results for the four fuel types.
4.3 Effect of the neutron spectrum
Figure 2 shows the effect of the various moderator materials on the transmutation rate for a cell with 30% fuel, 30% coolant and between 40 and 20% of structures. It is clear that the hydrogenated moderator ZrH2, which has a more efficient moderating effect, is the most effective to slow down the neutrons. However, its use in reactor is difficult mainly due to dissociation issues that were not taken into account here. The two other moderators are less efficient and their impact on the transmutation rate is consequently smaller. In each case, the impact on fission rate is inversely proportional to the impact on the transmutation rate. This is explained by the change in the spectrum which has already been discussed before.
However, this highlights a potential use of the moderator to accelerate transmutation kinetic. Using moderator material increases the total absorption cross-section and thus the transmutation rate while decreasing the fission cross-section. This leads to an increase in the production of curium and heavier minor actinides. However, using moderator appears as a possible solution to tune the production of curium with regards to cycle constraints in order to maximize the transmutation rate. This will be discussed in the next parts. It should also be noted that addition of moderating material may lead to damaging power peaking issues [11].
 |
Fig. 2 Transmutation rate versus moderator fraction. |
4.4 Effect of the MA isotopic vector and volume fraction
Increasing the minor actinides volume fraction in the fuel has two effects which are opposite. On the one hand, an increase in the MA fraction leads to a harder spectrum, which decreases the transmutation rate. On the other hand, the increase in the loaded fraction of minor actinides also increases the transmutation rate by displacing the fuel isotopic vector further way from its equilibrium value. The first effect is predominant at high fraction and the second one is more visible at low fraction. This can be seen on Figure 3, which shows the transmutation rate at 1000 EPFD versus the fraction of moderator and the fraction of minor actinides for 1015 n/cm2/s flux with 40% fuel at 20% Pu fraction and 20% structures. One can see that for a constant moderator volume fraction, the transmutation rate first increases with the minor actinides fraction and then decreases. This is seen with all kind of coolant/fuel combination, all moderator material and with Am only or all minor actinides. This means that there is an optimal value for MA fraction loaded in the fuel, which depends also on the moderator fraction. In our calculations, no impact of the minor actinides vector on the transmutation rate or fission was found. However, in a “true” reactor, this vector will have an impact on reactivity and safety coefficients of the reactor.
It should also be noted that the position of this optimum may not be adequate with regards to the minor actinides inventory management. Indeed, it corresponds to relatively low minor actinides fraction.
 |
Fig. 3 Transmutation rate versus fraction of moderator. |
4.5 Effect of flux level and irradiation time
At the first order, transmutation rates variation with regards both to flux level and irradiation time goes as 1 − e−φT so an increase in any of these two parameters will lead to an increase in the transmutation rate without any impact on the fission rate, which is verified by our calculations.
Consequently, there is an interest in using the highest possible flux level to accelerate the transmutation process. For irradiation time, the reasoning is similar but appropriate care should be taken with regards to the so-called “curium peak”, which can be seen on Figure 4.
This peak is due to the competition between the production of curium from capture on americium isotopes and the destruction of these curium nuclei by fission or capture. At beginning of irradiation, the americium fraction is high which leads to a high production rate of curium with a low consumption rate as the curium fraction is still low. The height of this peak is proportional to the ratio of absorption cross-sections of Cm and Am isotopes. In a fast flux, this ratio is lower than in an epithermal flux, thus explaining why the peak appears to be lower in case A on Figure 4, which corresponds to a fast spectrum than in case B which corresponds to a more degraded spectrum. Both cases were introduced as “extremal” spectrum that can be found in a fast reactor, either with a very energetic spectrum (case A) or a very degraded spectrum (case B). It should also be noted that evolution kinetic of the curium fraction depends on the absorption cross-sections of Cm and Am, which explains the difference observed in terms of evolution on Figure 4.
From the previous analysis, we can conclude that the most important parameters in terms of reactor design for transmutation purposes are the amount of minor actinides loaded in the core and the spectrum. The other parameters studied have an impact which is small compared to the impact of the two previous parameters, and thus they can be neglected in a first step of optimization.
5 Results from the fuel cycle analysis
5.1 Methodology
Considering the results obtained in the previous part, two limit cases were used for the fuel cycle parameters analysis and it is assumed that any intermediate case in terms of spectrum leads to intermediate results. These cases are described in Table 6. They correspond to the optimum in moderator and minor actinides fraction visible on Figure 3. Case A corresponds to an asymptotic case with a very fast spectrum while case B corresponds to a very degraded spectrum for a typical fast reactor. In both cases, a loading with the MA vector described in Table 2 was considered. A manufacturing time of 2 years was also taken into account for the calculations concerning the residual power and neutron source. Sensitivity to the manufacturing time was also assessed. A final point which was discussed is the total inventory in minor actinides in the fuel cycle, which is proportional to the cooling time.
Details of the cases used for the fuel cycle calculations.
5.2 Evolution of decay heat and neutron source
The evolution of decay heat and neutron source is plotted in Figure 5 for both cases. Several comments can be made here. The first point that should be made here is that the use of a moderator material to shift the spectrum leads to an increase in the Cm production and thus in the decay heat in neutron source. Second, the sharp decrease in the decay heat is due to the decay of 242Cm with a period of 163 days. Once 242Cm has disappeared, the decay heat is dominated by 244Cm and 238Pu which are longer-lived (respectively 18.1 years and 87 years). A consequence of this is that the feasibility of reprocessing with significant quantities of curium must be demonstrated in order to consider transmutation otherwise prohibitively long cooling delays will have to be considered. For case A, this leads to value around 25 W/kg and for case B this leads to a limit around 50 W/kg.
Additionally, given the very high decay heat level in the first year of cooling, manipulation of such spent fuel assembly will be more complicated than with regular fuel (standard MOX fuel). It should be noted here that the fission products contribution at short timescales was neglected here so Figure 5 is actually underestimating decay heat in the first 5 years of cooling. A sensitivity analysis showed that the main contributor to the decay heat after 5 years was 243Am which yields 244Cm by neutron capture. At shorter timescale, decay heat is dominated by 242Cm contribution which comes from 241Am.
Neutron source being essentially driven by 244Cm contribution, its timescale is different from decay heat load and its decrease slower. For comparison, a typical UOx spent fuel discharged at 47.5 GWd/t has a typical heat load of around 4 W/kg and a neutron source of 2000 n/s/g after 4 years of cooling. One can consequently conclude from this short analysis that an increase in the reprocessing limit both in terms of decay heat and neutron source will be necessary in order to avoid large cooling times and minor actinides in-cycle inventories.
 |
Fig. 5 Evolution of decay heat and neutron source versus cooling time. |
5.3 Impact on the transmutation performances
In the next paragraphs, we will consider case B, which is the most penalizing case in terms of neutron source and decay heat due to the “moderated” spectrum. An important point that can be made about Figure 6 is the difference between the irradiation transmutation rate and the cycle transmutation rate, which is explained by:
-
the increased fraction of 241Pu in the fuel due to the spectrum shift;
-
the longer cooling time due to the higher decay heat.
One can also see that there is an interest to maximize the allowable decay heat for reprocessing in order to increase the cycle transmutation rate of 241Am. The saturation effect observed around 35 W/kg is due to the hypothesis that the minimal cooling time is 5 years. The same behavior can be observed for neutron source. The small increase at low decay heat in the cycle transmutation rate is explained by the very long cooling which leads to decay of a significant fraction of 241Am (T 1/2 = 432 years). Minimizing the cooling time has also the interest of both minimizing the time necessary to reach an equilibrium situation and the total inventory of minor actinide.
However, more active fuel at reprocessing increases the losses during treatment and consequently increases the amount of long-lived wastes coming from spent fuel reprocessing. It also leads to the production of more active wastes, which necessitate more waste packages for final storage. Work is still ongoing to quantify the loss level and identify the optimum solution of the problem.
This phenomenon is not seen in case A as the use of a fast spectrum leads to a lower production of curium isotopes and a lower equilibrium fraction of 241Pu. Consequently, the cooling times are lower by a factor three compared to case B and the minimal value of 5 years is reached. However, the transmutation rate during irradiation is also divided by three and the cycle transmutation rate by two.
 |
Fig. 6 Transmutation rate of 241Am for irradiation and cycle versus limit on decay heat during reprocessing. |
5.4 Impact of the manufacturing time
It was also found that the manufacturing time has a non-negligible impact on the total time necessary to reach an equilibrium situation. Indeed, contrary to the cooling time which decreases with the number of cycles, manufacturing is the same for each cycle. An increase of 2 years in fabrication leads then to an increase of 2 years of each cycle. This effect is more visible in case A where residual heat load is lower so cooling time is also lower and the fabrication time share in the entire reprocessing time is higher.
5.5 Outline of an optimization methodology
The conclusion from this fuel cycle parameters analysis is then that optimization of a global transmutation strategy requires both the optimization of the irradiation and reprocessing parts. Indeed, the good performances obtained from a given reactor can be cancelled by non-adapted reprocessing specifications and delayed reprocessing times. More specifically, the irradiation time and spectrum should be tuned so as to maintain the cooling time within acceptable boundaries while keeping acceptable transmutation performances.
A new methodology of reactor design is currently being developed to take into account these results to settle a multi-recycling transmutation strategy. Bearing in mind technological limitations such as maximal residence fuel time, it is aimed at selecting the best spectrum that ensures an efficient transmutation while allowing reprocessing within acceptable limits. In a second step, a core image will be designed to obtain a relevant spectrum as close as possible to the optimal one while keeping adequate safety parameters.
6 Conclusions
An analysis of the various parameters influencing the performances of a transmutation strategy was carried out including parameters from the reactor and the cycle. The neutron spectrum and the volume fraction of minor actinides in the core were found to be the most relevant parameters for the core, while the cooling time through the limitations on decay heat and neutron source for reprocessing was identified as a critical parameter for the fuel cycle part. It was shown that an optimization of a transmutation strategy required considering at the same time parameters from the cycle and the reactor.
Further work is ongoing to add a third component to this analysis, namely the waste and final repository aspect. Indeed, a goal of transmutation strategy is to reduce the size of the final deep geological repository. The decay heat and alpha activity of the waste are the main constraints impacting the number of waste packages to be stored and thus the volume occupied by the repository. In a second time, a full implementation of the optimization methodology will be carried out taking into account the three sides of the problem along with additional options such as heterogeneous recycling.
References
- D. Warin, C. Rostaing, Recent progress in Advanced Actinide recycling process, in Informal Exchange Meeting on partitioning and transmutation, San Francisco, 2010 (NEA, 2010) [Google Scholar]
- NEA, Minor actinides burning in thermal reactors (NEA, Paris, 2013) [Google Scholar]
- NEA, Homogeneous versus heterogeneous recycling of transuranics in fast nuclear reactors (NEA, Paris, 2012) [Google Scholar]
- J. Tommasi, S. Massara, S. Pillon, M. Rome, Minor actinides destruction in dedicated reactors, in Informal Exchange Meeting on partitioning and transmutation, Mol, 1998 (NEA, 1998) [Google Scholar]
- C. Prunier, F. Boussard, L. Koch, M. Coquerelle, Some specific aspects of homogeneous Am and Np based fuels transmutation through the outcomes of the superfact experiment in PHENIX fast reactor, in GLOBAL 1993, Seattle (1993) [Google Scholar]
- J. Tommasi, M. Delpech, J.P. Grouiller, A. Zaetta, Long-lived waste transmutation in reactors, Nucl. Technol. 1111, 133 (1995) [Google Scholar]
- L. Buiron et al., Transmutation abilities of the SFR low void effect core concept CFV 3600 MWth, in ICAPP 2012, Chicago (2012) [Google Scholar]
- C. Chabert, C. Coquelet-Pascal, A. Saturnin, G. Mathonniere, B. Boullis, D. Warin, L.V.D. Durpel, M. Caron-Charles, C. Garzenne, Technical and economic assessment of different options for minor actinides transmutation: the French case, in GLOBAL 2011, Tokyo (2011) [Google Scholar]
- K. Kawashima, K. Sugino, S. Ohki, T. Okubo, Design study of a low sodium void reactivity core to accomodate degraded TRU fuel, Nucl. Technol. 3, 270 (2013) [Google Scholar]
- G. Rimpault, The ERANOS code and data system for fast reactor neutronic analyses, in PHYSOR, Seoul (2002) [Google Scholar]
- T. Wakabayashi, Improvement of core performance by introduction of moderators in a blanket region of fast reactors, Sci. Technol. Nucl. Ins. 103, 879634 (2013) [Google Scholar]
Cite this article as: Timothée Kooyman, Laurent Buiron, Sensitivity analysis of minor actinides transmutation to physical and technological parameters, EPJ Nuclear Sci. Technol. 1, 15 (2015)
All Tables
Effect of the fuel type for a cell with 6.5% Am, averaged over the results for the three coolant types.
Effect of the coolant material type for a cell with 6.5% Am, averaged over the results for the four fuel types.
All Figures
 |
Fig. 1 Algorithm used for multi-recycling simulation. |
| In the text | |
 |
Fig. 2 Transmutation rate versus moderator fraction. |
| In the text | |
 |
Fig. 3 Transmutation rate versus fraction of moderator. |
| In the text | |
 |
Fig. 4 Illustration of the curium peak for case A and B (detailed below in Tab. 6). |
| In the text | |
 |
Fig. 5 Evolution of decay heat and neutron source versus cooling time. |
| In the text | |
 |
Fig. 6 Transmutation rate of 241Am for irradiation and cycle versus limit on decay heat during reprocessing. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


