| Issue |
EPJ Nuclear Sci. Technol.
Volume 7, 2021
|
|
|---|---|---|
| Article Number | 10 | |
| Number of page(s) | 15 | |
| DOI | https://doi.org/10.1051/epjn/2021011 | |
| Published online | 11 June 2021 | |
https://doi.org/10.1051/epjn/2021011
Regular Article
CONRAD – a code for nuclear data modeling and evaluation
1
CEA, DAM, DIF, 91297 Arpajon, France
2
CEA, DES, IRESNE, 13108 Saint Paul lès Durance, France
* e-mail: cyrille.de-saint-jean@cea.fr
Received:
7
July
2020
Received in final form:
19
February
2021
Accepted:
18
May
2021
Published online: 11 June 2021
The CONRAD code is an object-oriented software tool developed at CEA since 2005. It aims at providing nuclear reaction model calculations, data assimilation procedures based on Bayesian inference and a proper framework to treat all uncertainties involved in the nuclear data evaluation process: experimental uncertainties (statistical and systematic) as well as model parameter uncertainties. This paper will present the status of CONRAD-V1 developments concerning the theoretical and evaluation aspects. Each development is illustrated with examples and calculations were validated by comparison with existing codes (SAMMY, REFIT, ECIS, TALYS) or by comparison with experiment. At the end of this paper, a general perspective for CONRAD (concerning the evaluation and theoretical modules) and actual developments will be presented.
© C. De Saint Jean et al., Published by EDP Sciences, 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The development in a modern language (C++ object-oriented programming) of the CONRAD code started more than ten years ago at CEA-Cadarache. It was first devoted to nuclear reactions model calculations in the resonance range with data assimilation procedures based on Bayesian inference (such as SAMMY [1] and REFIT [2]). At that time an emphasis was made on experimental time-of-flight simulation and the related experimental conditions description with appropriate corrections [3,4]. Furthermore, a common framework to treat all uncertainties involved in the nuclear data evaluation process: experimental uncertainties (statistical and systematic) as well as model parameter uncertainties was originally proposed. Between these first developments and the present code status, additional features were added to CONRAD such as new theoretical models, new experimental descriptions as well as new Bayesian analysis features. The aim of this paper is to present an overview of the current status of CONRAD-V1 in terms of developments (physics/analysis) as well as in terms of functionalities. For further details on mathematical methods and analysis results, references to appropriate papers are given.
2 Code organization and content
2.1 General principles
CONRAD is a code devoted to the evaluation of nuclear data as well as theoretical model developments. Evaluation consists in making the synthesis between experimental and theoretical nuclear physics knowledge to propose numbers (referred as nuclear data) that will be used by applications (nuclear energy applications, medical applications, etc.). CONRAD is thus organized in several major modules which are theoretical modules (theoretical nuclear physics), experimental modules (experiment description and related simulation capabilities), interface modules (input/output) and analysis modules (mainly Bayesian inference). The main idea driving CONRAD developments is to use as much as possible an object-oriented description of physical phenomena to allow a generic interface to analysis modules (derivative calculation, Bayesian inference…) and to add any kind of models (that can be nuclear models or anything else) in a simple manner. A developer’s Application Programming Interface (referred as API in the rest of the document) is proposed.
2.2 CONRAD API description
2.2.1 Generic Bayesian interface implementation
Even though CONRAD was first designed for cross section evaluation, a Bayesian interface was conceived in the prime years of its development. It consists in creating links between experimental results and theoretical calculations with a proper handling of related parameters. The first important notion is the AbstractModel API illustrated in Figure 1 with a simple UML plot. Examples of cross section models derived from the generic interface as well as a user defined model (MyModel) are given. In terms of C++ programming, it means that all model classes should inherit from this AbstractModel. Thus, this model which is associated to internal parameters will be updated during the analysis, its results will be asked during internal iterations of the Bayesian algorithms. For example, in Figure 1, the method getGradMap() must return the derivatives of the implemented model with respect to a list of its internal parameters. It is not necessary for the Bayesian module of CONRAD to know exactly the physical meaning of the parameters: only mathematical derivatives are used when the Bayesian inference is called through a minimization requiring derivatives algorithm.
Several models were implemented in CONRAD which allow other nuclear data type evaluation than cross section with a common philosophy. It means that all the mathematical methods developed for Bayesian studies (see Sect. 2.3) can be used for any model that respects the imposed interface. In the past few years, fission yields models [5,6], prompt fission neutron spectrum and multiplicities based on Madland-Nix model (see Sect. 2.5.4 for an example), thermal data models [7] and delayed neutron data models used in evaluation [8] were implemented. Further details on the results can be found in the related papers. One can notice that such an interface must be the simplest possible.
For the Bayesian procedure, a companion class to this AbstractModel is the ExperimentalModel class that permits a consistent comparison between model results and experimental data points. Figure 2 presents the diagram description of the ExperimentalModel class. It is very general and it allows the description and data assimilation of nearly all experimental results of interest. In addition, the fact that experiments can give data which are not directly comparable to nuclear observable given by models (for example, a transmission measurement is not directly a total cross section but is related via a functional of the form e −nσtot) is handled by this generic API.
One last important notion in CONRAD, is the notion of parameters. A dedicated set of parameter classes was designed which allows values, uncertainties and correlations handling for both model parameters and experimental ones. In CONRAD, parameters are vectors of uncertainties and their update during the Bayesian analysis are driving the adjustment of model results to experimental data. In addition, during an analysis, the parameter type can change: it can be fitted, sampled (for Monte Carlo analysis), marginalized (see Sect. 2.3), considered as constant but with uncertainties or ignored. This volatility of the parameter type is something important when defining a calculation scheme for your evaluation. Furthermore, one can notice that both theoretical and experimental parameters can be handled via the ExperimentalModel class (see Fig. 2).
 |
Fig. 1 UML diagram description of CONRAD AbstractModel interface. The API for model implementation (called specialization) is presented. |
 |
Fig. 2 Diagram description of CONRAD Experimentalmodel interface. |
2.2.2 Generic cross section interface implementation
For cross section evaluation, a lot of nuclear reaction models exist in the literature. They are associated to various energy domains, various channels (elastic, inelastic, fission, capture, etc.). It seems appropriate to share as much as possible common features for these calculations.
The idea is to share a common description by means of a nuclear process describing nuclear reactions and connection between in going and out going channels. This nuclear process will be used to map the nuclear reaction model calculations and allows the Cross Section model to handle properly and in detail the cross section calculations with two perspectives: a channel-to-channel cross section (that can be a small part of the cross section) or in terms of reaction (elastic, fission, absorption, etc.) which is a more evaluation oriented result. In other words, the Cross Section model level will count and classify everything that is related to the handling of quantum numbers J, π, s, ℓ and the connections between entrance and exit channels.
A major difference between the AbstractModel interface and the Cross Section interface resides in the Physics content of the Cross Section implementation. Furthermore, as previously stated, a lot of nuclear reaction models exists for various incident particle energy and for various channels. Nevertheless, this variety can be driven by a proper interface. Figure 3 shows the result of theprevious discussion in term of code implementation general philosophy for the CONRAD cross section model description (CrossSectionModel). A new nuclear reaction model implementation (called MyNuclearReactionModel in the figure) should respect the nuclear reaction model interface and the rest is handled by the upper level (CrossSectionModel). Nuclear models, depending on the studied phenomenology can take various forms, especially in the fast energy range. Figure 3 shows also additional details on the “matrioschka” associated to nuclear reaction models devoted to transmission calculations and how a new developer could incorporate his or her developments within CONRAD with a few API restrictions (MyOpticalModel, MyFissionModel, MyGammaStrenghtFunction, etc.). Adding any kind of transmission calculations easily gives to the nuclear physicists a variety of possibilities for their own analysis.
 |
Fig. 3 Simple diagram description of CONRAD CrossSectionmodel interface. The API for new models implementation (called specialization) for cross section is presented. The red box contains existing implementations and the blue one deals with new models development and the appropriate interface with existing code. |
2.3 Bayesian inference modules
2.3.1 Basic principles
It was stated in previous chapter that CONRAD contains modules for Bayesian inference analysis (comparison between model and experiments).
A briefreminder of the Bayesian inference will be given. Let  (i = 1…Ny) denote some experimentally measured variables, and let x⃗ denote the parameters defining the model (
(i = 1…Ny) denote some experimentally measured variables, and let x⃗ denote the parameters defining the model (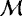 ) used to simulate these variables theoretically and t⃗ the associated calculated values to be compared with y⃗ (t⃗ is related to what was called in previous chapters the experimental functional). Using Bayes’ theorem [9] and especially its generalization to continuous variables [10], one can derive the following relation between conditional probability density functions (written p(.)) when the analysis of a new data set y⃗ is performed,
) used to simulate these variables theoretically and t⃗ the associated calculated values to be compared with y⃗ (t⃗ is related to what was called in previous chapters the experimental functional). Using Bayes’ theorem [9] and especially its generalization to continuous variables [10], one can derive the following relation between conditional probability density functions (written p(.)) when the analysis of a new data set y⃗ is performed,
 (1)
(1)
where U represents the “background” or “prior” information from which prior knowledge of x⃗ is assumed. y⃗ is supposed independent of U. In this framework, the denominator is just a normalization constant. t⃗ is connected to the experiment via the likelihood  term. For example, if the likelihood is supposed Gaussian it could be represented as:
term. For example, if the likelihood is supposed Gaussian it could be represented as:
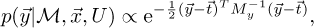 (2)
(2)
where My represents the experimental covariance matrix.
2.3.2 Major functionalities
The major functionalities implemented in CONRAD so far are: generalized chi-square minimization (in 2007), Bayesian Monte Carlo (in 2015) and special treatments for experimental systematic uncertainties (marginalization procedures in 2009). For a detailed explanation of these mathematical methods, see for example [11]. What is important to point out, is that CONRAD users can work with any of the previous developed methods without many changes in their input files. Simple keywords should be assigned but no drastic changes in the theoretical or experimental descriptions.
2.4 Experimental modules
The first version of CONRAD, CONRAD V0 [3], contains many C++ modules devoted to time-of-flight experiments: target description (isotopic contents, geometry), experimental parameters definition such as normalization and background related parameters. To allow a proper theoretical/experimental comparison, one has to know exactly the relationship between the theoretical cross sections and what is measured. The relationship between cross section and measurement is called a functional, named t⃗ in this document. All kinds of functional were proposed in CONRAD from the simplest one, macroscopic cross section (t⃗ ~ σ), to transmission (example given in Fig. 4 where what is measured is something close to t⃗ ~ e−σtotn) or capture yield measurements which exhibit a more complicated form (see [11,12] for some description of this experimental functional).
In addition, various physical models were implemented to allow Doppler broadening (temperature effects), experimental resolution functions simulation and multiple scattering models for thick targets [13]. Figure 5 shows a multiple scattering correction calculated by CONRAD on 55Mn neutron induced capture yields compared to a JRC-Geel measurement.
The major part of the recent experimental developments were related to the enhancement of these capabilities. In particular, Doppler broadening (from a Free-Gas Model to a Crystal Lattice Model [7]) to take into account better temperatureeffects (especially at low temperature), experimental apparatus resolution function (from simple analytic forms to user-provided tabulated functions), detector efficiency uncertainties, resonant scattering (to treat properly large targets) [14] and a lot of target corrections such as in-homogeneous material and porosity were proposed [4,15].
Furthermore, the possibility of using integral data measurements during the nuclear data evaluation was provided, for multigroup cross-section adjustments (see [16]) as well as for nuclear reaction model parameters (see [17]). This integral data assimilation can be done simultaneously with differential measurements assimilation or sequentially (after the differential analysis). For the latter solution, users can keep track of the analysis at each steps (parameters values, uncertainties and correlations) allowing a detailed booking of their calculations.
 |
Fig. 4 Comparison between experimental values and theoretical description for 238U neutron induced transmission. Figure taken from [11]. |
 |
Fig. 5 Comparison between experimental values and theoretical description with multiple-scattering corrections for 55 Mn neutron induced capture yields. Figure taken from [13]. |
2.5 Theoretical models
2.5.1 Cross section in the resonance energy range
The first theoretical developments in CONRAD were devoted to the calculation of cross sections in the resonance range base on R-matrix theory [18]. Several approximations were implemented from multilevel Breit-Wigner [19] to Reich-Moore [20]. A special treatment of the unresolved resonance range was proposed in the early years by implementing an average R-matrix [21] model in conjunction with a Hauser-Feshbach description of the nuclear reaction [22]. Fluctuation factor calculations (both Moldauer [23] and based on GOE description [24]) were implemented as well.
In the resonance range, R-matrix is a well defined theory with few hypothesis but with un-predicted parameters thus adjusted by comparison to experiments. A fitting procedure is mostly employed to obtain R-matrix parameters such as energies, and various widths of the resonances. The knowledge of these experiments, in other words all that is to be understood between electronic counts and the experimental values of the desired observable, is necessary to properly take into account for potential measurement biases.
2.5.2 Cross section in the fast energy range
The main evolution in the last CONRAD version is related to a philosophy change: from a resolved resonance range analysis code to a platform for nuclear data modeling. As a result, nuclear reaction models calculation capabilities were extended to the continuum region.
One should notice that for fast energy range (from several tenths of keV up to several tenths of MeV), several possibilities are offered by CONRAD: an encapsulation of TALYS [25] and/or ECIS [26] as well as a new optical model called CCCP. The CCCP module is a new C++ implementation for the resolution of the coupled-channel equations in the case of the symmetric rigid rotor model. The numerical resolution is based on the same Numerov or modified-Numerov that is used in the reference ECIS code. This new implementation is easier to maintain, it is free from numerical fix-ups necessary in single-precision computations and benefits from the use of the modern Eigen algebra library [27] allowing fast computations with a code written in a compact from. An exhaustive validation of this new optical model calculation was performed. Especially, one major point focusing on all the physical and numerical problems was the proper behaviour of CONRAD/CCCP coupled channels models for deformed nuclei (such as 157 Gd). Figure 6 shows a comparison for this isotope between this new C++ optical model calculation with the ECIS06 reference results based on the same optical potential and using the related optical potential parameters retrieved from the RIPL database [28]. Other cross sections such as shape elastic and reaction cross sections were validated as well. In the future the CCCP module should be extended to asymmetric rotation and rotational-vibrational models and multi-band coupling.
In addition to optical model calculations, several additional models were implemented in CONRAD (transmission models for each channel: Tγ, Tf, …) for partial crosssections to allow Hauser-Feschbach statistical model with fluctuation factor corrections (Moldauer and GOE already mentionned in the cross section in the resonance energy range chapter): transmission coefficient models for Gamma (Kopecky-Uhl [29]), transmission coefficient models for Fission (Hill-Wheeler [30], Cramer-Nix [31]) and level densities (Gilbert-Cameron [32]). An example for (n,γ) cross section of 56Fe is given in Figure 7. It shows the comparison between a full CONRAD calculation (based on all implemented models) and TALYS1.4.
For a full treatment of all actinides cross sections, a development of a first pre-equilibrium model based on the two excitons model [33] is underway.
 |
Fig. 6 ECIS06/CONRAD (aka CCCP) total cross section comparisons on 157Gd. |
 |
Fig. 7 TALYS1.4/CONRAD (n,γ) cross section comparisons on 56Fe. |
2.5.3 A meta-model for cross section calculations
As explained in the previous section, CONRAD contains nuclear reaction models for the whole energy range giving a cross section calculation capability from 0 eV up to 20 MeV. In CONRAD, by having this object oriented philosophy, it was quite easy to propose a full energy range cross section model where several models used for different energy ranges are embedded. This multi-modelcould be used for cross section evaluation in the whole energy range with the same physical (channels, quantum numbers, reactions…) and mathematical (Bayesian inference) descriptions. Indeed, evaluations are most of the time done by separating fast energy range and resonance energy range, creating not only discontinuities in the evaluation of the cross sections but also block diagonal matrices when covariance analysis is performed. CONRAD by having the whole nuclear reaction models in the same tool allows the evaluation of cross section over the entire energy range of interest with an experiment having measures on a broad energy range. The example of the new JEFF-3.2 (and JEFF-3.3 [34]) sodium evaluation is given in Figure 8.
One can see the cross correlation between the resonance (below 2 MeV) and the continuum energy range (above 2 MeV). It comes from the analysis of the new JRC-Geel experiment with both a Reich-Moore model and an optical model. The correlation is created first because CONRAD provides the framework to handle several nuclear reaction models (or codes) but from a more fundamental point of view because, the code gives the possibility of treating experimental systematic uncertainties (such as normalization). In this sodium analysis, the Rouki data [36] exhibits a 2.6% normalization uncertainty which is reflected in the evaluated cross section uncertainty but also in the cross correlation between energy domains. Indeed, it was shown in [37] that without any systematic uncertainties, no cross correlations appears between energy domains if models are not sharing common parameters.
 |
Fig. 8 New covariance evaluation with CONRAD of 23Na (n, n′) cross section [35] based on the analysis of JRC/Geel inelastic cross section measurements [36]. Figure taken from [11]. |
2.5.4 Fission observable models
As mentioned several time in this paper, CONRAD interface allows the implementation of other models than only cross section and nuclear reaction models. In particular, a lot of work was devoted to develop several models associated to post-fission nuclear data.
Prompt fission neutron spectrum and multiplicity
Prompt fission neutron spectrum and multiplicity models based on Watt [38] or Madland-Nix [39] models were implemented for evaluating the covariances. In Figure 9, the result of a prompt fission neutron spectrum on 235 U evaluation is shown.
This evaluation builds on a previous work [40]. The main advance was to be able to handle properly various systematic experimental uncertainties such as normalisation (important for this kind of experiment because most of the time the measurements do not cover the whole neutron spectrum and thus no normalisation is given) as well as detector efficiencies. In addition, one can see in this figure, the scatter and discrepancies to be dealt by the evaluation. As expected, high uncertainties are obtained in the tails due to a lack of good experimental data. The generic Bayesian interface (ExperimentalModel) allows the utilization of all the mathematical methods developed in the Bayesian inference module such as marginalisation of experimental parameters and/or Bayesian Monte-Carlo without additional developments.
Fission Yields
With the same philosophy than previously exposed, fission yields covariances evaluation [6] was made for JEFF-3.1.1 nuclear data library for 235,238U, 239,240Pu based on Wahl [41] and Brosa [42] models. The main goal was to reproduce coherently the JEFF-3.1.1 fission yield library for the latter isotopes and add covariance information. There is a room for improvement in this kind of evaluation by implementing new models (replacing Wahl or Brosa) or by interfacing to existing codes (such as GEF [43]). In the future, one can propose new evaluations from scratch based on advanced models and an exhaustive set of experiments.
 |
Fig. 9 235U thermal neutron induced prompt fission neutron spectra evaluation with CONRAD. Comparison between experiment and theory (Madland-Nix Los Alamos model) are given, as well as an uncertainty evaluation. Figure courtesy of A. Chebboubi. |
2.5.5 Miscellaneous model implementations
Allowing any kind of model to connect with the code via a definite C++ interface (see Fig. 1) opens the range of various additional nuclear data analysis. So far, the following models were also implemented or interfaced:
-
models for thermal data calculation [7];
-
DPA cross sections models [44];
-
expression-based model: description given with standard mathematical functions in the input file.
In addition, a Miscellaneous analysis mode has been developed for testing new nuclear data models before their implementations in the CONRAD code. This mode allows to explore a large variety of analysis by using the full Bayesian capabilities of CONRAD without specific C++ development nor model description in the input file.
One of the latest applications of the Miscellaneous mode was the production of covariance matrices between the model parameters involved in the description of the Thermal Scattering Laws (TSL), which are needed to describe the neutron scattering process when energies lie below a few eV. Figure 10 shows the correlation matrix obtained for the total cross section of H in H2O at 574K. The uncertainty analysis mainly relies on the experimental phonon density of states of H in H2O recommended in the JEFF-3.1.1 library. Improved results were obtained by using the CAB model for water established at the nuclear center of Bariloche (Argentina) thanks to Molecular Dynamic simulations. The correlation matrix between theMolecular Dynamic parameters obtained from the least-squares fit of neutron data are discussed in reference [45].
 |
Fig. 10 Relative uncertainties and correlation matrix for the total cross section of H in H2O at 574K obtained with the Miscellaneous analysis mode of CONRAD by using the TSL parameters of JEFF-3.1.1. |
3 The user interface
3.1 General principles for users
With CONRAD-V1, major analyses performed are of Bayesian inference type. Users can adjust theoretical models with a given set of parameters on a given set of experiments knowing some prior information. The analysis can be performed sequentially (adjustmentdone experiment after experiment) or simultaneously (all experiments adjusted at the same time) and with a standard generalized least-square engine or by Monte Carlo [46]. In addition, marginalization of nuisance parameters [47,48], which consists of taking properly into account parameters necessary to described the theoretical/experimental comparison but unnecessary for the final nuclear reaction model evaluation is possible. For example, experimental parameters such as normalization, detector efficiencies…can be treated that way. Multi-model calculations where a given observable, such as a cross section, can be modeled on different energy ranges by different nuclear reaction models can be performed. Analysis devoted to diagnosed the input data such as sensitivity calculations, which gives the normalized derivatives of a model related to an observable to its parameters (numerically or analytically) and statistical analysis of resonances [49] are available.
In the next chapters, two kind of analysis will be detailed (in particular the files description). The first one is a standard evaluation analysis of neutron induced cross section of 239 Pu. This analysis makes use of implemented nuclear reaction models in the code. The second analysis related to delayed neutron takes advantage of a very new CONRAD feature: the expression based model where the model is not directly implemented in the CONRAD code but described in the input file with simple mathematical functions. Both analysis are of Bayesian type. For the users, the inputs for any Bayesian inference can be separated in three types of files. The first file, called the analysis file, describes the calculation to be made (generalized least-square or Monte Carlo or another one…) as well as the path to theoretical and experimental input files (one can have several of them) and also various global parameters (numerical parameters, number of processes for multi-threaded calculations, etc.). CONRAD executable only needs a consistent analysis file. The second important kind of files, called theoretical files, contains the theory description, the related parameters values and uncertainties with a defined “type” that can be fixed (do nothing), fitted (or sampled in the Monte Carlo case) or marginalized. In addition, theses files contain the nuclear process description to be investigated. The last files, called experimental files, contain the description of the experiments in terms of experimental conditions (temperature, target compositions, etc.), experimental parameters (also with described types: fixed, fitted, marginalized and having uncertainties) and the experimental data with their uncertainties.
These files contains simple associations between keys and values that can be numbers, strings and list of the previous items as can be seen in following examples.
3.2 An example of cross section evaluation analysis
An example of necessary files is given in the following. It corresponds to the evaluation of 239 Pu resonance parameters on a fission cross section measurement.
First, let us describe the analysis file.

The keyCalculationType is explicitly what is driving the calculation. In this example, you choose to perform a simple generalized χ2 adjustment. As such, you need to give additional indications on the calculation: NumberOfProcess is the desired number of threads for parallelization of the calculation, nbIterations and epsilon are related to the Newton-Raphson algorithm in CONRAD.
To perform a Bayesian analysis, replace “ANALYSIS” by “BMC_ANALYSIS” and just add the following specific Monte-Carlo keys:

An experimental file path is given by the key Experiment which is equal to “./Experiment/Pu9FissWest93.exp” in this example. The content of the experimental file is of the following type:

In this file, you can find keys related to experimental conditions (temperature, target composition), to experimental parameters (EffectiveTemperature key) and to the measurements itself ([/Spectrum/]). In addition, you can choose also the model to be used for Doppler broadening (FreeGas in this example).
A theoretical file path is given by the key Theory which is equal to “./Theory/pu9Jeff.th” in this example. The content of this file is of the following type:

This theoretical file contains the nuclear process description as well as the scope of the calculation (which compound nucleus), the chosen theory and the related parameters (resonance parameters in this example). One can see also how parameters are described for the analysis: FITTED, CONSTANT (with uncertainties) or fixed (no uncertainties).
In the previous files all experimental points (~4000) were given and all resonances were compiled, we showed only part of the files for the sake of clarity (there are 1044 resonances in the file for 239Pu). The result of this analysis is given in Figure 11.
 |
Fig. 11 239Pu resonance parameters adjustment on a fission cross section measurement. Theoretical/experimental comparisons before an after adjustment. |
3.3 An example of expression based analysis on delayed neutron data
3.3.1 Expression based model
A recent development allows the user to give a model based on standard mathematical functions described in the input file. A generic C++ expression interpreter was coded and no additional C++ model development was necessary.
To explain with a simple example, let us look at the following file representing a model with three parameters p1, p2 and p3:

This model can be fitted on experimental data (called dataType1) represented as:

This simple example shows the idea of the expression based model capabilities. In the following chapter, a much more complicated use of this functionality is presented.
3.3.2 Delayed neutrons evaluation
Delayed neutron data covariances were evaluated using this new capability (model based on standard mathematical functions described in the input file). For the delayed neutron model based on summation calculation, it was a very challenging case for this CONRAD capability.
Indeed, let us remind the expression used to calculate multiplicities of delayed neutrons:
![\[ \nu_{\text{d}}=\lim_{t_{\text{irr}}\rightarrow\infty} \left(\sum_{1}^n x_i N_i(t_{\text{irr}}) P_{n,i}\right) \]](/articles/epjn/full_html/2021/01/epjn200017/epjn200017-eq6.png)
where xi is is the number of delayed neutrons emitted during the decay, Ni(tirr) is the concentration of the ith precursor and Pn,i is the probability for delayed-neutron emission after the β− decay of precursor i. The number of precursor is about 1000 and for each of them an equation is related to the calculation of Ni (tirr). A partial (in terms of visible input) example of the written equations is given by the following expressions written in the theoretical input file:

The previous equation for dataType_235Ut corresponds to the solution of a Bateman equation involving all precursors for the delayed neutron multiplicity of 235U for thermal neutrons. The previous file corresponds to the marginalization of all branching ratios (, etc. BR44, BR45, etc.) and evaluate their impact on delayed neutron multiplicities. This kind of analysis was used to calculate neutron delayed data values and covariances for 235,238U and 239,240,241Pu [50].
4 Towards a new version
4.1 Simplification and re-engineering of the code
The CONRAD code was initiated more than ten years ago with original ideas related to resolved resonance range analysis. The increase of code functionalities (new models, Monte Carlo algorithms) led to a code harder to maintain and sometimes difficult to understand for new developers. It was thus decided to redevelop and simplify a lot what was formerly done with a special emphasize on the ExperimentalModel API as well as model implementation capabilities. In addition, efforts are put on accelerating calculations with optimizations, new numerical methods and a better design of parallelism. Speed is still an issue to allow good and comprehensive full range evaluation (resonance of actinides or iron for example), uncertainty evaluation, high energy range data assimilation (with uncertainties) etc ..., These developments are underway and all former functionalities have not yet been transferred to the new CONRAD version.
4.2 Charged particles and compound nucleus representation of nuclear reactions
The historical way of supplying evaluated cross section in the resolved resonance range for actinides consists in providing resonance parameters. These latter are associated to the laboratory framework of the incident particle. For lighter nuclei, more sophisticated resonances parameters needs to be evaluated. Former limitations of the ENDF format used to prevent the supply of resonance parameters for light nuclei. This limitation being now removed, the new code will aim at evaluating such lighter isotopes.
In Figure 12 inspired by E. Vogt in [51], one can see how the 7 Be compound nucleus can be formed/decay through various channels. The idea, recently developed in the CONRAD code, is to work with parameters defined in the center of mass of the system and analyze measurements of various cross sections yielding the same compound nucleus with different target/projectile. The use of alternative measurements implies the necessity to treat channels with charged particles that experience Coulomb potential. Several developments were necessary, namely for computing penetration factors with accurate Coulomb functions [52]. An example of such an analysis is given in Figure 13, where both 6Li and 3He data were analyzed for the compound nucleus 7 Be formation [53].
In addition, new developments are ongoing in order to implement the Brune alternative parametrization [54] of the R-matrix. This parametrization removes the presence of the arbitrary boundary conditions and yields eigenstate energies located at the observed resonance energy.
 |
Fig. 12 Schematic view of the 7Be compound nucleus with channel surfaces and radii (left) and formation and decay through various channels (right). |
 |
Fig. 13 Simultaneous analysis of measurements involving the same compound system. Up is the comparison of CONRAD on Barnard 1964 4He(3He,3He) measurements. Bottom is the comparison of CONRAD (with the same model than previously) on Fasoli 1964 6 Li(p, p) measurements. |
4.3 Bayesian inference
4.3.1 Statistical indicators
The evaluation of nuclear data is mainly based on nuclear reaction model comparisons with experiments within a Bayesian inference mathematical framework. Very few statistical discussions arise from this inference. Especially, the notion of goodness of the fit is notclearly exposed. Various potential Bayesian indicators that may be standard in the Bayesian inference community but not really used in the framework of nuclear data assimilation can be proposed (and very recently developed in CONRAD code) for evaluating the correctness of the adjustment. These indicators are Akaike information criteria [55], Bayesian information criterion [56], deviance information criterion, Cook’s distance (some examples of the use of Cook’s distance are given in [16]). In addition, a mathematical definition of an effective number of parameters following [57] was recently proposed in CONRAD as:
 (3)
(3)
where, Nparam is the number of initial parameters used in the fit, Mprior is the prior covariance matrix between the initial parameters and Mposterior is the posterior covariance matrix. The interpretation of this formulae is quite obvious: it is a competition between an initial guess of the complexity represented by Nparam and a penalty relying on the deviance between the prior and the posterior ( ).
).
With these indicators a common framework is proposed for addressing general questions such as, model complexity, over-fitting and comparison of complex models to infer a possible best choice. The use of Monte Carlo Bayesian inference (in complement or instead of traditional generalized least square) implemented in the CONRAD code is a suitable mathematical framework for calculating these indicators. Some first attempts are given in [58,59].
4.3.2 Model deficiencies
one major hypothesis is that probability density functions are given as “knowing” the model which does not mean that the model is correct.
Two solutions can be offered and are under development in CONRAD. The first one, is to treat the model inadequacies from a statistical point of view by adding an extra model (model deficiency) reflecting somehow the incapacity of these theories to fit experimental data [60,61]. Higher uncertainties (of the model prediction) are expected due to this lack of knowledge. The second one is to obtain reference calculations based on microscopic theoretical description which are far from being effective. Nevertheless, the effort should be expanded to obtain, at least for some part of the nuclear models, microscopic ingredients. These calculations can thus be used as reference calculations for phenomenological models. Resulting calculated biases must be taken into account during Bayesian inference.
4.4 Towards microscopic calculation ingredients
The new CONRAD code is designed to allow a lot of innovative developments for nuclear physics models. The ultimate goal of nuclear physics modeling could be thought as the removal of some free (adjusted) parameters in nuclear reaction models as well as in fission models. This path may lead to more consistency from the physics point of view on nuclear models, give information/evaluation for isotopes difficult to measure (such as fission products) and reduce compensation effects. Following what was exposed in [62], fission barrier calculations are a real room for improvement in nuclear data evaluation, namely in the resonance range, where for instance no energy-dependence is used in practice for the penetration factor used for fission channels. Reduction of arbitrariness of the adjusted parameters can also be an intermediate goal. For instance, phenomenological models implemented in CONRAD to mimic fission penetration factors can be used to extract more physical fission amplitudes [62] from experimental data. The ambition in CONRAD is to go even further by using fission models [63] based on macroscopic-microscopic and microscopic calculations. This model can be used to study the deformation energy of a compound nucleus as it deforms towards fission yielding potential energy surface (PES). This PES can be projected on a one-dimensional deformation potential energy that can be further used in a numerical approach of fission barrier tunneling. The obtained transmission coefficient can finally be used as a replacement of the extremely idealized Hill-Wheeler approach.
In addition, CONRAD will be able to take into account microscopic ingredients coming from microscopic calculations such as level densities computed from Hartree-Fock-Bogolyubov calculations [64] or gamma strength function based on QRPA calculations [65]. These ingredients are very valuable and will be used in the future at CEA in a broader way for doing evaluations in JEFF project.
5 Conclusions
CONRAD after more than ten years of developments is a code mature for nuclear data evaluation with any kind of nuclear models. The major functionalities of this code are Bayesian inference modules, possibilities of calculation of cross sections with several models to cover the whole energy range of interest (from 0 eV to 20 MeV) and an exhaustive treatment of all uncertainties coming from experiments. These developments were constantly tested, verified and validated against other nuclear reaction codes. In addition, pragmatic choices were made to use existing codes such as ECIS or TALYS with a proper C++ encapsulation allowing to use these tools in the same way than in-house developments. The strategy was then to rewrite some of them in C++, for a better use of additional modern features such as parallelization (on PC’s) or for high performance computing on large calculators. Furthermore, this will facilitate the development of new models and prepare the use of microscopic ingredients.
Author contribution statement
All authors participate in the writing and correction of the paper. C. De Saint Jean, P. Archier and P. Tamagno are principal recent developers of the CONRAD code.
- 1.
C. De Saint Jean: general coordination and contribution in all the chapters and calculation of the 239 Pu example.
- 2.
P. Tamagno: main contribution in the chapters Theoretical models and Towards a new version.
- 3.
P. Archier: main contribution in the chapter Theoretical models and calculation related to Figure 8.
- 4.
G. Noguere: main contribution in the chapters Experimental modules and Miscellaneous model implementation.
Acknowledgements
The authors would like to thank (alphabetical order) L.Berge-Tamagno (prompt fission neutron spectrum), O.Bouland, D.Bernard, A. Chebboubi (prompt fission neutron spectrum), S. Chen, M. Diakaki, D. Foligno (delayed neutron evaluations), B. Habert (experimental uncertainties and marginalization), P. Leconte, O. Litaize (experimental description and capture yields), A. Nizigama, E. Privas (Bayesian Monte Carlo), D. Regnier, O. Serot, C. Suteau (numerical R-matrix derivatives and generalized Chi-Square solver), N. Terranova (fission yields), C. Vaglio-Gaudard, E. Vandermeersch and S. Xu for their past, present or future involvement in the CONRAD activity, as users and/or developers.
References
- N.M. Larson, Updated users’ guide for SAMMY: Multilevel R-matrix fits to neutron data using Bayes’ equation, tech. rep., ORNL/TM-9179/R8 ENDF-364/R2, 2006 [Google Scholar]
- M.C. Moxon, T.C. Ware, C.J. Dean, REFIT-2009 A Least-Square Fitting Program for Resonance Analysis of Neutron Transmission, Capture, Fission and Scattering Data Users’ Guide for REFIT-2009-10, tech. rep., UK Nuclear Science Forum Report UKNSF, 2010 [Google Scholar]
- C. De Saint Jean, B. Habert, O. Litaize, G. Noguère, C. Suteau, Status of CONRAD, a nuclear reaction analysis tool,’ EDP Sciences 1, 251–254 (2008) [Google Scholar]
- P. Archier, C. De Saint Jean, O. Litaize, G. Noguère, L. Berge, E. Privas, and P. Tamagno, CONRAD evaluation code: development status and perspectives, Nucl. Data Sheets 118, 488–490 (2014) [CrossRef] [Google Scholar]
- N. Terranova, O. Serot, P. Archier, C. De Saint Jean, M. Sumini, Covariance matrix evaluations for independent mass fission yields, Nucl. Data Sheets 123, 225–230 (2015) [CrossRef] [Google Scholar]
- N. Terranova, O. Serot, P. Archier, C.D.S. Jean, M. Sumini, Fission yield covariance matrices for the main neutron-induced fissioning systems contained in the JEFF-3.1.1 library, Ann. Nucl. Energy 109, 469–489 (2017) [CrossRef] [Google Scholar]
- G. Noguère, P. Maldonado, C. De Saint Jean, Doppler broadening of neutron-induced resonances using ab initio phononspectrum, Eur. Phys. J. Plus 133, 177 (2018) [CrossRef] [Google Scholar]
- D. Foligno, P. Leconte, O. Serot, O. Litaize, A. Chebboubi, Summation calculation of delayed neutron yields for 235U, 238U and 239Pu, based on various fission yield and neutron emission probability databases, EPJ Web Conf. 193, 03004 (2018) [CrossRef] [Google Scholar]
- M. Bayes, M. Price, An essay towards solving a problem in the doctrine of chances, Philos. Trans. 53, 370–418 (1763) [NASA ADS] [CrossRef] [Google Scholar]
- A. Papoulis, S.U. Pillai, Probability, Random Variables, and Stochastic Processes. McGraw-Hill series in electrical engineering: Communications and signal processing, Tata McGraw-Hill (2002) [Google Scholar]
- C. De Saint Jean, P. Archier, E. Privas, G. Noguère, B. Habert, P. Tamagno, Evaluation of neutron-induced cross sections and their related covariances with physical constraints, Nucl. Data Sheets 148, 383–419 (2018). Special Issue on Nuclear Reaction Data. [CrossRef] [Google Scholar]
- P. Schillebeeckx, B. Becker, Y. Danon, K. Guber, H. Harada, J. Heyse, A. Junghans, S. Kopecky, C. Massimi, M. Moxon, N. Otuka, I. Sirakov, K. Volev, Determination of resonance parameters and their covariances from neutron induced reaction cross section data, Nucl. Data Sheets 113, 3054–3100 (2012). Special Issue on Nuclear Reaction Data. [CrossRef] [Google Scholar]
- O. Litaize, P. Archier, B. Becker, P. Schillebeeckx, S. Kopecky, Validation of capture yield calculations in the resolved resonance energy range with CONRAD code, EPJ Web Conf. 42, 02003 (2013) [CrossRef] [Google Scholar]
- B. Becker, R. Dagan, G. Lohnert, Proof and implementation of the stochastic formula for ideal gas, energy dependent scattering kernel, Ann. Nucl. Energy 36, 470–474 (2009) [CrossRef] [Google Scholar]
- P. Archier, C. De Saint Jean, S. Kopecky, O. Litaize, G. Noguère, P. Schillebeeckx, K. Volev, Recent developments in the CONRAD code regarding experimental corrections, EPJ Web Conf. 42, 02004 (2013) [CrossRef] [EDP Sciences] [Google Scholar]
- M. Salvatores, G. Palmiotti, G. Aliberti, R. McKnight, P. Archier, C. De Saint Jean, E. Dupont, M. Herman, M. Ishikawa, K. Sugino, T. Ivanova, E. Ivanov, S.-J. Kim, I. Kodeli, A. Trkov, G. Manturov, S. Pelloni, C. Perfetti, B. Rearden, A. Plompen, D. Rochman, W. Wang, H. Wu, W.-S. Yang, Methods and issues for the combined use of integral experiments and covariance data, tech. rep., Organization for Economic Co-operation and Development-Nuclear Energy Agency (OECD-NEA), WPEC-33, December 2013. NEA/NSC/WPEC/DOC(2013)445 [Google Scholar]
- C. De Saint Jean, P. Archier, E. Privas, G. Noguère, O. Litaize, P. Leconte, Evaluation of cross section uncertainties using physical constraints: focus on integral experiments, Nucl. Data Sheets 123, 178–184 (2015) [CrossRef] [Google Scholar]
- A.M. Lane, R.G. Thomas, R-matrix theory of nuclear reactions, Rev. Mod. Phys. 30, 257–353 (1958) [CrossRef] [MathSciNet] [Google Scholar]
- G. Breit, E.P. Wigner, Capture of slow neutrons, Phys. Rev. 49, 519–531 (1936) [CrossRef] [Google Scholar]
- C.W. Reich, M.S. Moore, Multilevel formula for the fission process, Phys. Rev. 111, 929–933 (1958) [CrossRef] [Google Scholar]
- P.A. Moldauer, Average compound-nucleus cross sections, Rev. Mod. Phys. 36, 1079–1084 (1964) [CrossRef] [Google Scholar]
- W. Hauser, H. Feshbach, The inelastic scattering of neutrons, Phys. Rev. 87, 366–373 (1952) [NASA ADS] [CrossRef] [Google Scholar]
- P.A. Moldauer, Evaluation of the fluctuation enhancement factor, Phys. Rev. C 14, 764–766 (1976) [CrossRef] [Google Scholar]
- J.J.M. Verbaarschot, H.A. Weidenmüller, M.R. Zirnbauer, Grassmann integration in stochastic quantum physics: the case of compound-nucleus scattering, Phys. Rep. 129, 367–438 (1985) [CrossRef] [MathSciNet] [Google Scholar]
- A.J. Koning, S. Hilaire, M.C. Duijvestijn, TALYS-1.0, EDP Sci. 1, 211–214 (2008) [Google Scholar]
- J. Raynal, Notes on ECIS94, Tech. Rep. CEA-N-2772, pp. 1–145, Commisariat à l’Énergie Atomique, Saclay, France, 1994 [Google Scholar]
- G. Guennebaud, B. Jacob et al., Eigen v3. http://eigen.tuxfamily.org (2010) [Google Scholar]
- R. Capote, M. Herman, P. Obložinský, P.G. Young, S. Goriely, T. Belgya, A.V. Ignatyuk, A.J. Koning, S. Hilaire, V.A. Plujko, M. Avrigeanu, O. Bersillon, M.B. Chadwick, T. Fukahori, Z. Ge, Y. Han, S. Kailas, J. Kopeckỳ, V.M. Maslov, G. Reffo, M. Sin, S. Soukhovitskii, Efrem, P. Talou, RIPL – Reference input parameter library for calculation of nuclear reactions and nuclear data evaluations, Nucl. Data Sheets 110, 3107–3214 (2009) [NASA ADS] [CrossRef] [Google Scholar]
- J. Kopecky, M. Uhl, Test of gamma-ray strength functions in nuclear reaction model calculations, Phys. Rev. C 41, 1941–1955 (1990) [CrossRef] [Google Scholar]
- D.L. Hill, J.A. Wheeler, Nuclear constitution and the interpretation of fission phenomena, Phys. Rev. 89, 1102–1145 (1953) [NASA ADS] [CrossRef] [Google Scholar]
- J.D. Cramer, J.R. Nix, Exact calculation of the penetrability through two-peaked fission barriers, Phys. Rev. C 2, 1048–1057 (1970) [CrossRef] [Google Scholar]
- A. Gilbert, A.G.W. Cameron, A composite nuclear-level density formula with shell corrections, Can. J. Phys. 43, 1446–1496 (1965) [CrossRef] [Google Scholar]
- J.J. Griffin, Statistical model of intermediate structure, Phys. Rev. Lett. 17, 478–481 (1966) [CrossRef] [Google Scholar]
- A.J.M. Plompen, O. Cabellos, C. De Saint Jean, M. Fleming, A. Algora, M. Angelone, P. Archier, E. Bauge, O. Bersillon, A. Blokhin, F. Cantargi, A. Chebboubi, C. Diez, H. Duarte, E. Dupont, J. Dyrda, B. Erasmus, L. Fiorito, U. Fischer, D. Flammini, D. Foligno, M.R. Gilbert, J.R. Granada, W. Haeck, F.-J. Hambsch, P. Helgesson, S. Hilaire, I. Hill, M. Hursin, R. Ichou, R. Jacqmin, B. Jansky, C. Jouanne, M.A. Kellett, D.H. Kim, H.I. Kim, I. Kodeli, A.J. Koning, A.Yu. Konobeyev, S. Kopecky, B. Kos, A. Krása, L.C. Leal, N. Leclaire, P. Leconte, Y.O. Lee, H. Leeb, O. Litaize, M. Majerle, J.I. Márquez Damián, F. Michel-Sendis, R.W. Mills, B. Morillon, G. Noguère, M. Pecchia, S. Pelloni, P. Pereslavtsev, R.J. Perry, D. Rochman, A. Röhrmoser, P. Romain, P. Romojaro, D. Roubtsov, P. Sauvan, P. Schillebeeckx, K.H. Schmidt, O. Serot, S. Simakov, I. Sirakov, H. Sjöstrand, A. Stankovskiy, J.C. Sublet, P. Tamagno, A. Trkov, S. van der Marck, F. Álvarez-Velarde, R. Villari, T.C. Ware, K. Yokoyama, G. Zerovnik, The joint evaluated fission and fusion nuclear data library, jeff-3.3, Eur. Phys. J. A 56, 181 (2020) [CrossRef] [EDP Sciences] [Google Scholar]
- P. Archier, G. Noguère, C. De Saint Jean, A.J. Plompen, C. Rouki, New JEFF-3.2 sodium neutron induced cross-sections evaluation for neutron fast reactors applications: from 0 to 20 MeV, Nucl. Data Sheets 118, 140–143 (2014) [CrossRef] [Google Scholar]
- C. Rouki, P. Archier, C. Borcea, C. De Saint Jean, J. Drohé, S. Kopecky, A. Moens, N. Nankov, A. Negret, G. Noguère, A.J. Plompen, M. Stanoiu, High resolution measurement of neutron inelastic scattering cross-sections for 23 na, Nucl. Instr. Methods Phys. Res. A 672, 82–93 (2012) [CrossRef] [Google Scholar]
- C. De Saint Jean, E. Privas, P. Archier, G. Noguère, Estimation of nuclear reaction model parameter covariances and the related neutron induced cross sections with physical constraints, Nucl. Data Sheets 118, 336–340 (2014) [CrossRef] [Google Scholar]
- B.E. Watt, Energy spectrum of neutrons from thermal fission of u235, Phys. Rev. 87, 1037–1041 (1952) [CrossRef] [Google Scholar]
- D.G. Madland, J.R. Nix, New calculation of prompt fission neutron spectra and average prompt neutron multiplicities, Nucl. Sci. Eng. 81, 213–271 (1982) [CrossRef] [Google Scholar]
- L. Berge, Contribution à la modélisation des spectres de neutrons prompts de fission. Propagation d’incertitudes sur un calcul de fluence cuve. PhD thesis, Institut polytechnique de Grenoble (2015) [Google Scholar]
- A.C. Wahl, Nuclear-charge distribution and delayed-neutron yields for thermal-neutron-induced fission of 235U, 233U, and 239Pu and for spontaneous fission of 252Cf, Atom. Data Nucl. Data Tables 39, 1–156 (1988) [NASA ADS] [CrossRef] [Google Scholar]
- U. Brosa, S. Grossmann, A. Müller, Nuclear scission, Phys. Rep. 197, 167–262 (1990) [NASA ADS] [CrossRef] [Google Scholar]
- K.-H. Schmidt, B. Jurado, C. Amouroux, C. Schmitt, General description of fission observables: Gef model code, Nuclear Data Sheets 131, 107–221 (2016) [CrossRef] [EDP Sciences] [Google Scholar]
- S. Chen, P. Tamagno, D. Bernard, P. Archier, G. Noguere, From nuclear physics to displacement damage calculation and uncertainty propagation in Conrad, Results Phys. 17, 103023 (2020) [CrossRef] [Google Scholar]
- J. Scotta, G. Noguère, J.M. Damian, Generation of the h in h2o neutron thermal scattering law covariance matrix of the cab model, EPJ Nucl. Sci. Technol. 4, 1–12 (2018) [CrossRef] [Google Scholar]
- C. De Saint Jean, E. Privas, P. Archier, G. Noguère, On the use of Bayesian Monte-Carlo in evaluation of nuclear data, in International Conference on Nuclear Data for Science and Technology - ND2016, JRC, Geel, Bruges, Belgium, September 5–9, 2016 [Google Scholar]
- C. De Saint Jean, G. Noguère, B. Habert, B. Iooss, A Monte Carlo approach to nuclear model parameter uncertainties propagation, Nucl. Sci. Eng. 161, 363–370 (2009) [CrossRef] [Google Scholar]
- B. Habert, C. De Saint Jean, G. Noguère, L.C. Leal, Y. Rugama, Retroactive generation of covariance matrix of nuclear model parameters using marginalization techniques, Nucl. Sci. Eng. 166, 276–287 (2010) [CrossRef] [Google Scholar]
- O. Litaize, C. De Saint Jean, G. Noguère, P. Archier, Statistical analysis of a set of actinide resolved resonance parameters with CONRAD code, J. Korean Phys. Soc. 59, 1900–1903 (2011) [CrossRef] [Google Scholar]
- D. Foligno, New evaluation of delayed-neutron data and associated covariances. Theses, CEA Cadarache, 13115 SAINT-PAUL-LEZ-DURANCE; Aix Marseille Université, CNRS, Centrale Marseille, ED 353 Sciences pour l’ingénieur, Mécanique, physique, micro et nanoélectronique, 2019 [Google Scholar]
- E. Vogt, Theory of low energy nuclear reactions, Rev. Mod. Phys. 34, 723–747 (1962) [CrossRef] [Google Scholar]
- N. Michel, Precise coulomb wave functions for a wide range of complex ℓ, η and z, Comput. Phys. Commun. 176, 232–249 (2007) [CrossRef] [Google Scholar]
- I.J. Thompson, R. Deboer, P. Dimitriou, S. Kunieda, M.T. Pigni, G. Arbanas, H. Leeb, T. Srdinko, G. Hale, P. Tamagno, P. Archier, Verification of r-matrix calculations for charged-particle reactions in the resolved resonance region for the 7Be system, Eur. Phys. J. A 55, 92 (2019) [CrossRef] [EDP Sciences] [Google Scholar]
- C.R. Brune, Alternative parametrization of R-matrix theory, Phys. Rev. C 66, 044611 (2002) [CrossRef] [Google Scholar]
- H. Akaike, Information theory and an extension of the maximum likelihood principle, in Proc. 2nd Int. Symp. Information Theory (2001) 267–281 [Google Scholar]
- G. Schwarz, Estimating dimension of a model, Ann. Stat. 6, 461–464 (1978) [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- D.J. Spiegelhalter, N.G. Best, B.P. Carlin, A. Van Der Linde, Bayesian measures of model complexity and fit, J. Royal Stat. Soc. B 64, 583–639 (2002) [Google Scholar]
- D. Kumar, S.B. Alam, H. Sjöstrand, J.-M. Palau, C. De Saint Jean, Influence of nuclear data parameters on integralexperiment assimilation using Cook's distance, EPJ Web Conf. 211, 07001 (2019) [CrossRef] [Google Scholar]
- D. Kumar, S.B. Alam, H. Sjöstrand, J.M. Palau, C. De Saint Jean, Nuclear data adjustment using Bayesian inference, diagnostics for model fit and influence of model parameters, EPJ Web Conf. 239, 13003 (2020) [CrossRef] [Google Scholar]
- H. Leeb, D. Neudecker, T. Srdinko, Consistent procedure for nuclear data evaluation based on modeling, Nucl. Data Sheets 109, 2762–2767 (2008) [CrossRef] [Google Scholar]
- D. Neudecker, R. Capote, H. Leeb, Impact of model defect and experimental uncertainties on evaluated output, Nucl. Instr. Methods Phys. Res. A 723, 163–172 (2013) [CrossRef] [Google Scholar]
- P. Tamagno, C. De Saint Jean, O. Bouland, G. Noguère, P. Archier, E. Privas, O. Serot, From low- to high-energy nuclear data evaluations – issues and perspectives on nuclear reaction models and covariances, Eur. Phys. J. A 51, 181 (2015) [CrossRef] [EDP Sciences] [Google Scholar]
- P. Tamagno, Challenging fission cross section simulation with long standing macro-microscopic model of nucleus potential energy surface. PhD thesis, Université de Bordeaux, 2015 [Google Scholar]
- A.J. Koning, S. Hilaire, S. Goriely, Global and local level density models, Nucl. Phys. A 810, 13–76 (2008) [CrossRef] [Google Scholar]
- S. Goriely, S. Hilaire, S. Péru, The gogny-hfb+qrpa dipole strength function and its application to radiative neutron capture cross section, EPJ Web Conf. 178, 04001 (2018) [CrossRef] [Google Scholar]
Cite this article as: Cyrille De Saint Jean, Pierre Tamagno, Pascal Archier, Gilles Noguere, CONRAD, a code for nuclear data modeling and evaluation, EPJ Nuclear Sci. Technol. 7, 10 (2021)
All Figures
 |
Fig. 1 UML diagram description of CONRAD AbstractModel interface. The API for model implementation (called specialization) is presented. |
| In the text | |
 |
Fig. 2 Diagram description of CONRAD Experimentalmodel interface. |
| In the text | |
 |
Fig. 3 Simple diagram description of CONRAD CrossSectionmodel interface. The API for new models implementation (called specialization) for cross section is presented. The red box contains existing implementations and the blue one deals with new models development and the appropriate interface with existing code. |
| In the text | |
 |
Fig. 4 Comparison between experimental values and theoretical description for 238U neutron induced transmission. Figure taken from [11]. |
| In the text | |
 |
Fig. 5 Comparison between experimental values and theoretical description with multiple-scattering corrections for 55 Mn neutron induced capture yields. Figure taken from [13]. |
| In the text | |
 |
Fig. 6 ECIS06/CONRAD (aka CCCP) total cross section comparisons on 157Gd. |
| In the text | |
 |
Fig. 7 TALYS1.4/CONRAD (n,γ) cross section comparisons on 56Fe. |
| In the text | |
 |
Fig. 8 New covariance evaluation with CONRAD of 23Na (n, n′) cross section [35] based on the analysis of JRC/Geel inelastic cross section measurements [36]. Figure taken from [11]. |
| In the text | |
 |
Fig. 9 235U thermal neutron induced prompt fission neutron spectra evaluation with CONRAD. Comparison between experiment and theory (Madland-Nix Los Alamos model) are given, as well as an uncertainty evaluation. Figure courtesy of A. Chebboubi. |
| In the text | |
 |
Fig. 10 Relative uncertainties and correlation matrix for the total cross section of H in H2O at 574K obtained with the Miscellaneous analysis mode of CONRAD by using the TSL parameters of JEFF-3.1.1. |
| In the text | |
 |
Fig. 11 239Pu resonance parameters adjustment on a fission cross section measurement. Theoretical/experimental comparisons before an after adjustment. |
| In the text | |
 |
Fig. 12 Schematic view of the 7Be compound nucleus with channel surfaces and radii (left) and formation and decay through various channels (right). |
| In the text | |
 |
Fig. 13 Simultaneous analysis of measurements involving the same compound system. Up is the comparison of CONRAD on Barnard 1964 4He(3He,3He) measurements. Bottom is the comparison of CONRAD (with the same model than previously) on Fasoli 1964 6 Li(p, p) measurements. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



