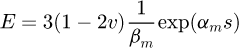| Issue |
EPJ Nuclear Sci. Technol.
Volume 6, 2020
Euratom Research and Training in 2019: the Awards collection
|
|
|---|---|---|
| Article Number | 1 | |
| Number of page(s) | 7 | |
| DOI | https://doi.org/10.1051/epjn/2019059 | |
| Published online | 03 January 2020 | |
https://doi.org/10.1051/epjn/2019059
Regular Article
Effects of the initial granular structure of clay sealing materials on their swelling properties: experiments and DEM simulations
1
Université Paris-Est, Laboratoire Navier, UMR 8205 (Ecole des Ponts ParisTech − Ifsttar − CNRS), 6-8 avenue Blaise Pascal, Cité Descartes, 77455 Marne-la-Vallée Cedex 2, France
2
Andra R&D, 1-7 rue Jean Monnet, Parc de la Croix-Blanche, 92298 Châtenay-Malabry Cedex, France
* e-mail: benjamin.darde@enpc.fr
Received:
20
October
2019
Accepted:
8
November
2019
Published online: 3 January 2020
Pellet-based expansive clay materials are considered as a sealing material for closing the galleries in radioactive waste disposal concepts. In repository conditions, the granular mixture progressively homogenises upon hydration by the host rock pore water. The present study focuses on the material behaviour before homogenisation. A grain-scale experimental characterisation is first performed in the laboratory. A model describing the hydromechanical behaviour of a pellet is proposed based on the experimental results. Then, suction-controlled swelling pressure tests are performed in the laboratory. Using Discrete Element Method (DEM) and the model proposed for a single pellet, the tests are successfully simulated. It is highlighted that (i) the swelling pressure evolves in two phases in the investigated suction range, controlled by the granular structure of the mixture; (ii) wall effects at the laboratory scale affects the material response; (iii) measurement variability associated to the sensor diameter is non-negligible; (iv) DEM is a valuable tool able to provide insight into the material behaviour.
© B. Darde et al., published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Concepts of radioactive waste disposal vary between the different countries. A general feature of the repository concepts is the reliance on the multi-barrier principle [1], which for a HLW repository consists of: (i) a canister containing waste, (ii) a host rock, and (iii) an engineered barrier system that also limits fluid flow in the repository.
Compacted expansive clay-based materials are candidate materials for engineered barriers in radioactive waste disposal concepts. These materials are characterised by a low permeability, good radionuclide retention capacity, and ability to swell upon hydration and thus filling technological voids and exerting a confining pressure on the excavation damaged zone.
Owing to operational convenience, pellet-based materials have been considered as an alternative to compacted blocks [2–5]. Pellets are emplaced in the galleries as a granular material. The granular material undergoes hydration by the pore water of the host rock and progressively becomes homogeneous. Before homogenisation, the mechanical behaviour of the material is controlled by its granular nature. The influence of the initial granular structure on the macroscopic response of the material upon hydration needs to be characterised to better understand the engineered barrier evolution under repository conditions.
The present work focuses on the study of the influence of the granular structure on the macroscopic response upon hydration under constant-volume conditions. Suction-controlled swelling pressure tests are performed in the laboratory. These tests are simulated using the Discrete Element Method (DEM) to obtain insight into grain-scale phenomena. Finally, interesting results regarding the performance of swelling pressure tests in the laboratory and the DEM model results contributing to the characterisation of the influence of the granular structure are presented and discussed.
2 Material
2.1 Bentonite pellet
In the French concept of radioactive waste disposal [6], 32-mm subspherical MX80 bentonite pellets are envisaged as one element of the engineered barriers. In the present study, a smaller version of this pellet is used to perform laboratory tests. Pellets are composed of a central cylinder with two spherical ends (Fig. 1). The initial properties of the pellet are presented in Table 1.
 |
Fig. 1 Geometry of the pellet. |
Initial properties of the pellet.
2.2 Pellet assembly
Swelling pressure tests are performed for a pellet assembly. The average dry density of the granular material is 1.05 Mg/m3. The pellet volume fraction (ratio of volume of pellet to total volume) is 0.553.
3 Work performed
3.1 Description of the hydromechanical behaviour of a pellet
A model describing the hydromechanical behaviour of a pellet is required to perform DEM simulations of pellet assemblies. The experimental characterisation of the pellet behaviour in the laboratory has been performed and is described in [7]. In the experimental study, the vapour equilibrium technique [8] is used to impose a suction to pellets. At equilibrium, the volumetric strain of the pellet is measured using a camera. Pellet Young modulus and strength are obtained through compression tests. Evolution of the pellet volumetric strain, Young modulus, and strength is measured upon suction decrease.
Assuming that (i) the pellet macroporosity is negligible, (ii) pellet behaviour remains elastic, (iii) pellets are fully saturated and expand upon water uptake, and (iv) pellet strength is proportional to pellet stiffness, the following equations are used to describe the pellet behaviour upon suction decrease:
 (2)
(2)
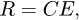 (3)where E is the pellet Young modulus, εV
is the pellet volumetric strain, R is the pellet strength, ν is the pellet Poisson ratio, s is the suction, s
0 is the initial suction, αm
, βm
and C are parameters.
(3)where E is the pellet Young modulus, εV
is the pellet volumetric strain, R is the pellet strength, ν is the pellet Poisson ratio, s is the suction, s
0 is the initial suction, αm
, βm
and C are parameters.
Parameters used in the model for the 7-mm pellet are presented in Table 2. Figure 2 presents a comparison between model predictions and experimental results.
The model aims at describing the pellet behaviour upon partial hydration, before losing the granular structure. Experimental results in the literature suggest that, for MX80 bentonite, the model would no longer be valid for suction below ∼3 to ∼7 MPa [9]. The model assumptions are discussed in [7].
 |
Fig. 2 Experimental results and model predictions: left, pellet Young modulus and strength and right, pellet volumetric strain [7]. |
3.2 Vapour hydration of pellet assemblies under constant-volume conditions
Two swelling pressure tests are carried out and referred to as SP1 and SP2. Isochoric cylindrical cells are used to perform swelling pressure tests. Two porous disks are placed at the bottom and at the top of the cell. Humid air is allowed to directly flow from the bottom to the top of the cell through a side tube. The side tube prevents increase of air pressure and allows humid air to diffuse in the inter-pellet porosity. 209 pellets are placed in the cell to reach the target pellet volume fraction. Diagrams of the isochoric cell are presented in Figure 3. Dimensions of the cell are presented in Table 3.
Hydration is performed using the vapour equilibrium technique. Upon pellet hydration, owing to the constant-volume conditions, swelling pressure develops against the cell walls. This latter is measured by an axial pressure sensor. Suction considered in the study are: 82 MPa, 59 MPa, 40 MPa, 38 MPa, 25 MPa, 13 MPa, 9 MPa, and 4 MPa. A new suction step starts when equilibrium is reached at the current suction. Equilibrium is considered when swelling pressure remains constant for three days.
 |
Fig. 3 Diagram of the experimental apparatus used for swelling pressure tests: left, 3D view of the isochoric cell and right, sketch of the suction control system. |
Dimensions of the isochoric cell used for swelling pressure tests.
3.3 DEM simulations of laboratory tests
In the DEM simulations, the pellet assembly is modelled as a sphere assembly. Each sphere behaves as a pellet, according to the model presented in Section 3.1. The sphere diameter is denoted by a. Its initial value, a 0, is chosen such that its volume and density are the same as for the real pellets. The cell is modelled as a cylinder of infinite Young modulus. The cylinder dimensions are the same as the cell used in the laboratory. Simulations consist of two steps: (i) sample preparation and (ii) pellet hydration.
During the simulations, the granular assembly is always under gravity. Interactions at contacts are described by normal and tangential reactions. Normal forces are elastic-perfectly plastic. Elastic limit is set to the pellet strength (Eq. (3)). Tangential reaction is described using a simplified form of the Cattaneo-Mindlin-Deresiewicz laws [10] and the Coulomb friction as in [11], denoting by µ the friction coefficient for all contacts. Damping in contacts is considered as in [11]. Elastic normal forces are calculated using Hertz's law as follows: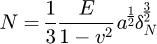 (4)or
(4)or
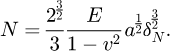 (5)
(5)
Equation (4) is used for contacts between two pellets. Equation (5) is used for contacts between a pellet and an infinitely stiff flat wall. In both expressions, N is the normal force and δN is the normal deflection (Fig. 4).
Sample preparation is performed by placing 209 pellets in the cell. The first 20 pellets are placed at random positions at the bottom of the cell. Then, pellets are placed one by one at the lowest available elevation in the rigid cylinder each 1 second. When all pellets are placed, the elevation of the top of the cylinder is set at the elevation of the highest pellet, then progressively decreased to its target elevation. During preparation step, µ is set to 0 in the model to avoid high initial pressure to arise during the closure step. Following preparation, µ is set to 0.3. Hydration is modelled as an increase of the diameter of all pellets. Swelling pressure is calculated as the sum of normal forces on the area corresponding to the pressure sensor. The area corresponding to the pressure sensor can be set to the same area as in experiments, or a larger/smaller area to study the influence of this parameter.
At each calculation step (i.e. decrease of the elevation of the top wall or diameter increase) the granular assembly is considered at equilibrium in the model when both the ratio of the net force to the maximum normal force and the ratio of the net moment to the maximum moment are smaller than 10−4 for each pellet. The next step starts when this condition is fulfilled.
100 simulations are performed to assess the reproducibility of the results. Parameters used for the simulations are summarised in Table 4.
 |
Fig. 4 Left: contact between two pellets i and j of diameter ai and aj , distance between centres dij , and normal deflection δN ij . Right: evolution of normal force as a function of normal deflection. |
Parameters used in the DEM simulations of swelling pressure tests.
4 Results
4.1 Evolution of the swelling pressure upon suction decrease in the experiments
Both SP1 and SP2 tests displays comparable swelling pressure-suction relationships upon hydration. First, hydration is characterised by an increase of the measured swelling pressure. Then, a plateau/decrease of swelling pressure is measured.
Following the cell closure, the initial pressure in SP1 is 0.055 MPa. Upon hydration from initial state (s = s 0 =89 MPa) to s = 40 MPa, swelling pressure increases from 0.055 MPa to 0.173 MPa. Then, the swelling pressure remains nearly constant until s = 25 MPa and decreases and reaches 0.128 MPa at s = 9 MPa.
Following the cell closure, the initial pressure in SP2 is 0.010 MPa. Upon hydration from initial state to s = 9 MPa, swelling pressure increases from 0.010 MPa to 0.153 MPa. Then, swelling pressure decreases and reaches 0.135 MPa at s = 4 MPa.
A picture of the samples is taken at s = 9 MPa (SP1) and s = 4 MPa (SP2). Both materials are still granular at these values of suction. Pellets and inter-pellet voids can be identified. The pellets still have the same shape as initially. Some pellets in contact with the top wall are irreversibly deformed at the contact area. It is not known if the deformation occurred during cell closure or as a result of the hydration and subsequent swelling of the pellets (Fig. 5).
The evolution of swelling pressure upon suction decrease in SP1 and SP2 is presented in Figure 6.
 |
Fig. 5 Pictures of samples following hydration: left, SP1 and right, SP2. |
 |
Fig. 6 Comparison of experimental and numerical evolution of swelling pressure upon suction decrease. Dashed lines represent a two-standard-deviation interval of numerical simulation results. |
4.2 Evolution of the swelling pressure upon suction decrease in the simulations
The DEM results are presented for an identical sensor diameter in the simulations as in the experiments. The mean value of swelling pressure (for 100 calculated samples) evolves in two phases upon hydration.
Following the cell closure, the initial pressure in the DEM simulations is negligible. Upon hydration from initial state to s = 60 MPa, the swelling pressure increases to 0.330 MPa. Then, the swelling pressure decreases and reaches 0.110 MPa at s = 4 MPa.
The simulation results are presented in Figure 6 along with SP1 and SP2 measurements. Variability of the apparent swelling pressure is determined by calculating the standard deviation for the 100 simulations. In Figure 6, a two-standard-deviation interval is plotted to highlight the result variability. Variability of simulation results is discussed in the following section.
4.3 Evolution of the pellet-scale features in the simulations
The evolution of the proportion of plastic contacts in the simulated samples, xplas , is calculated upon suction decrease (mean value for the 100 samples). Following the cell closure, xplas is zero. Upon hydration from s = 89 MPa to s = 70 MPa, the swelling pressure increases still with a constant xplas = 0. Between s = 70 MPa and s = 60 MPa, xplas sharply increases. This suction range corresponds to the peak swelling pressure. Then, swelling pressure keeps decreasing while xplas keeps increasing (Fig. 7).
Notable differences are obtained between xplas and xplas sup , the proportion of plastic contacts among contact between pellets and with the top wall of the cell. Between s = 70 MPa and s = 60 MPa, xplas sup increases from xplas sup = 0 to xplas sup = ∼0.80 (Fig. 7).
The mean value (for the 100 samples) of the increment of elastic normal deflection in the contacts between the pellets and the top wall, where swelling pressure is measured, as a function of the imposed increment of pellet radius (i.e. a/2) is presented in Figure 8. The two values are almost identical until the peak value is reached, as highlighted in Figure 8 by plotting a “y = x” line.
 |
Fig. 7 Evolution of the proportion of plastic contacts and swelling pressure upon suction decrease in the simulated samples. |
 |
Fig. 8 Calculated increment of the mean elastic deflection in the contacts between the pellets and the top wall, as a function of the imposed increment of pellet radius. The dashed line represents the “y = x” line. |
4.4 Influence of the sensor size on the apparent macroscopic response
Depending on the position of pellet-top wall contacts, the simulation results can be characterised by different calculated swelling pressure depending on the chosen sensor diameter. The influence of the sensor size on the variability of the measured swelling pressure is determined by considering different values of the sensor diameter. The mean value for the 100 simulations is found to be close for all sensor diameters. The coefficient of variation is defined as the ratio of the standard deviation to the mean value. Figure 9 presents the value of the coefficient of variation for the swelling pressure at peak value and at s = 9 MPa, for different values of the sensor diameter, for the 100 simulated samples.
Figure 9 highlights that (i) variability significantly increases for diameter ratios smaller than 4, (ii) variability is lower at low suction than at peak and (iii) even at diameter ratio of 6 the coefficient of variation is non-negligible (∼0.10).
 |
Fig. 9 Calculated coefficient of variation of the swelling pressure as a function of the ratio of pressure sensor diameter to initial pellet diameter. |
5 Discussion
5.1 Validity of the DEM modelling approach
The validity of the DEM approach depends mainly upon the following assumptions: (i) the material remains granular and (ii) contact laws used are adequate to describe interactions between pellets.
Sample dismantling allowed the material to be observed. It is highlighted in Figure 5 that the pellet assembly remained granular at suctions as low as 4 MPa. Pellets are still subspherical. Modelling the pellet assembly as a sphere assembly is considered appropriate within the investigated suction range.
The contact laws used in the present study assume that the pellets are characterised by an elastic-perfectly plastic behaviour. Experimental results [7] suggest that pellet behaviour is not fully reversible before reaching pellet strength. However, the same contact law is used in [7] to satisfactorily reproduce the force-displacement relationship in compression tests. Irreversible deformations observed in Figure 5 suggest that using plasticity is an adequate approach compared to grain crushing to account for pellet strength.
The model is able to reproduce the two phases of evolution of the swelling pressure. The peak swelling pressure is overestimated by the model. It is considered to be a consequence of modelling the pellets by equivalent beads of exactly the same stiffness and strength. As highlighted in Figure 2, the pellet properties are characterised by a non-negligible variability at high suction. Accounting for these variations in the model would decrease the peak swelling pressure and apparent stiffness before the peak since (i) the pellet Young modulus could be characterised by significantly lower values at high suction and (ii) xplas would start to increase at higher suction.
Upon hydration at lower suction, it is expected that the material will undergo microstructural rearrangement [9]. Owing to the material dry density, a final swelling pressure of ∼0.25 MPa can be estimated [12]. The model can neither handle the microstructural rearrangement nor the second increase of swelling pressure. It is considered that it is no longer valid at suction lower than ∼3 MPa, as for the model for a single pellet.
5.2 Influence of the initial granular structure
In pellet materials, interaction at contacts have been suggested to control the material response upon suction decrease [5,13]. Experimental results highlight that the material remains granular at low suction, with dry inter-pellet porosity. DEM simulations provide insight into grain-scale phenomena. Comparison of experimental and numerical simulation results suggests that the swelling pressure of bentonite pellet materials evolves in two phases upon suction decrease, which are controlled by the interaction at the contacts. At high suction, swelling pressure increases as a result of pellet swelling. This phase is mainly controlled by the pellet stiffness. As contact forces between pellets start to reach the pellet strength, swelling pressure reaches a plateau/decreases upon suction decrease. This phase is characterised by irreversible deformation at contacts and is mainly controlled by the decrease of pellet strength and stiffness upon suction decrease.
5.3 Influence of the cell walls
In a true representative elementary volume, the variability of the results would be negligible. In the present work, simulation results highlight that, even with a ratio of pressure sensor diameter to pellet diameter of 6 (i.e. sensor diameter of 45 mm, for a cell diameter of 60 mm), the coefficient of variation of swelling pressure is non-negligible.
It is also evidenced that each increment of pellet radius is associated to an equivalent increment of deflection in contacts between pellets and the top wall. This is possible if no rearrangement of the granular assembly occurs. Owing to the low volume fraction of the granular assembly, this is considered as a consequence of wall effect due to the small size of the cell.
Influence of the wall is also highlighted by comparing the evolution of xplas and xplas sup . The absence of particle rearrangement induces a faster increase of xplas sup , because contact stiffness is higher in pellet-wall contacts (Eqs. (4) and (5)). In this respect, the measured post-peak swelling pressure in small size cells can be overestimated [14].
It is thus recommended to either use larger cells to perform swelling pressure tests, or carefully interpret and compare experiments performed at laboratory scale using comparable cell size to pellet size ratios.
5.4 Measurement of swelling pressure
In addition to the variability associated to the small size of the cell, simulation results highlight that significant measurement variation can be obtained for small pressure sensors. DEM allowed this variability to be quantified. It is suggested that the results of laboratory-scale swelling pressure tests performed on pellet materials should be interpreted even more carefully if the ratio of sensor diameter to pellet diameter is low.
6 Conclusion
The present work addressed the hydromechanical behaviour of bentonite pellet materials upon partial hydration, in a suction range which allows the behaviour of the material to be controlled by its granular structure.
From grain-scale experimental characterisation in the laboratory, a DEM modelling approach was presented. Using DEM, suction-controlled swelling pressure tests performed in the laboratory on pellet materials were successfully simulated.
It was highlighted that, upon suction decrease from 89 MPa to ∼3 MPa, the swelling pressure evolves in two phases: (i) an increase of swelling pressure, controlled by pellet stiffness and (ii) a decrease of swelling pressure, characterised by irreversible deformation at contacts, controlled by the decrease of pellet strength and stiffness.
Numerical simulation results evidenced that the behaviour of pellet material in swelling pressure tests performed at laboratory scale are influenced by the small size of the cell. In addition, variability of the apparent swelling pressure associated to the sensor size was quantified and shown to be non-negligible.
Author contribution statement
The present study is a part of the PhD thesis of B. Darde, supervised by A.M. Tang and co-supervised by the other co-authors. The code used to perform DEM simulations is developed by J.-N. Roux. The model for pellets has been added to the code by B. Darde. Experiments have been performed by B. Darde. All authors discussed the results and contributed to the final version of the manuscript.
References
- P. Sellin, O.X. Leupin, Clays Clay Miner. 61, 477 (2014) [Google Scholar]
- G. Volckaert, F. Bernier, E.E. Alonso, A. Gens, J. Samper, M.V. Villar, P.L. Martín, J. Cuevas, R. Campos, H.R. Thomas, C. Imbert, V. Zingarelli, EUR 16744. Commission of the European Communities, Luxembourg, 1996 [Google Scholar]
- M. van Geet, G. Volckaert, S. Roels, Appl. Clay Sci. 29, 73 (2005) [CrossRef] [Google Scholar]
- C. Imbert, M.V. Villar, Appl. Clay Sci. 32, 197 (2006) [Google Scholar]
- C. Hoffmann, E.E. Alonso, E. Romero, Phys. Chem. Earth. 32, 832 (2007) [Google Scholar]
- Andra, Evaluation of the feasibility of a geological repository in an argillaceous formation. Andra, Chatenay-Malabry, France, 2005 [Google Scholar]
- B. Darde, A.M. Tang, J.M. Pereira, J.N. Roux, P. Dangla, J. Talandier, M.N. Vu, Geotech. Lett. 8, 330 (2018) [CrossRef] [Google Scholar]
- A.M. Tang, Y.J. Cui, Can. Geotech. J. 42, 287 (2005) [Google Scholar]
- N. Saiyouri, D. Tessier, P.Y. Hicher, Clay Miner. 39, 469 (2004) [CrossRef] [Google Scholar]
- K.L. Johnson, Contact Mechanics (Cambridge University Press, Cambridge, UK, 1985) [CrossRef] [Google Scholar]
- I. Agnolin, J.N. Roux, Phys. Rev. E 76, 1 (2007) [Google Scholar]
- Q. Wang, A.M. Tang, Y.J. Cui, P. Delage, B. Gatmiri, Eng. Geol. 124, 59 (2012) [CrossRef] [Google Scholar]
- E.E. Alonso, C. Hoffmann, E. Romero, J. Rock Mech. Geotech. Eng. 2, 12 (2010) [Google Scholar]
- B. Darde, J.N. Roux, P. Dangla, J.M. Pereira, A.M. Tang, J. Talandier, M.N. Vu, in CIGOS 2019, Innovation for Sustainable Infrastructure (Springer, Singapore, 2020), p. 871 [CrossRef] [Google Scholar]
Cite this article as: Benjamin Darde, Anh Minh Tang, Jean-Noël Roux, Patrick Dangla, Jean-Michel Pereira, Jean Talandier, Minh Ngoc Vu, Effects of the initial granular structure of clay sealing materials on their swelling properties: experiments and DEM simulations, EPJ Nuclear Sci. Technol. 6, 1 (2020)
All Tables
All Figures
 |
Fig. 1 Geometry of the pellet. |
| In the text | |
 |
Fig. 2 Experimental results and model predictions: left, pellet Young modulus and strength and right, pellet volumetric strain [7]. |
| In the text | |
 |
Fig. 3 Diagram of the experimental apparatus used for swelling pressure tests: left, 3D view of the isochoric cell and right, sketch of the suction control system. |
| In the text | |
 |
Fig. 4 Left: contact between two pellets i and j of diameter ai and aj , distance between centres dij , and normal deflection δN ij . Right: evolution of normal force as a function of normal deflection. |
| In the text | |
 |
Fig. 5 Pictures of samples following hydration: left, SP1 and right, SP2. |
| In the text | |
 |
Fig. 6 Comparison of experimental and numerical evolution of swelling pressure upon suction decrease. Dashed lines represent a two-standard-deviation interval of numerical simulation results. |
| In the text | |
 |
Fig. 7 Evolution of the proportion of plastic contacts and swelling pressure upon suction decrease in the simulated samples. |
| In the text | |
 |
Fig. 8 Calculated increment of the mean elastic deflection in the contacts between the pellets and the top wall, as a function of the imposed increment of pellet radius. The dashed line represents the “y = x” line. |
| In the text | |
 |
Fig. 9 Calculated coefficient of variation of the swelling pressure as a function of the ratio of pressure sensor diameter to initial pellet diameter. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.