| Issue |
EPJ Nuclear Sci. Technol.
Volume 5, 2019
|
|
|---|---|---|
| Article Number | 7 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/epjn/2019003 | |
| Published online | 15 May 2019 | |
https://doi.org/10.1051/epjn/2019003
Regular Article
Quick calculation of damage for ion irradiation: implementation in Iradina and comparisons to SRIM
1
DEN, Service de Recherches de Métallurgie Physique, CEA, Université Paris-Saclay,
91191
Gif-sur-Yvette, France
2
DEN, Service de Thermique et Mécanique des Fluides, CEA, Université Paris-Saclay,
91191
Gif-sur-Yvette, France
* e-mail: jpcrocombette@cea.fr
Received:
8
February
2019
Received in final form:
1
March
2019
Accepted:
29
March
2019
Published online: 15 May 2019
Binary collision approximation (BCA) calculation allows for two types of damage calculation: full cascade and quick calculations. Full cascade mode describes fully the cascades while in quick calculations, only the trajectory of the ion is followed and effective formulas give an estimation of the damage resulting from each collision of the ion. We implement quick calculation of damage in the Iradina code both for elemental and multi-component solids. Good agreement is obtained with SRIM. We show that quick calculations are unphysical in multi-component systems. The choice between full cascade and quick calculations is discussed. We advise to favour full cascade over quick calculation because it is more grounded physically and applicable to all materials. Quick calculations remain a good option for pure solids in the case of actual quantitative comparisons with neutron irradiations simulations in which damage levels are estimated with the NRT (Norgett-Robinson and Torrens) formulas.
© J.-P. Crocombette and C. Van Wambeke, published by EDP Sciences, 2019
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In the nuclear context, ion irradiation is used as a way to study materials under radiation. Such experiments are cheaper and quicker than in reactor studies under neutron irradiation. Direct connection of such ion experiments with neutron irradiations face numerous challenges [1,2]. However, even without a direct connection to in-reactor experiments, ion irradiation gives many information about the behaviour of materials. Rapid numerical estimations of the damage and implantation profiles in ion irradiation experiments are very important. They are used before the irradiations to design them, and/or after experiments to choose where analyses should be performed. Such estimations requires fast modelling tools of the primary damage and implantation profiles. The Binary collision approximation (BCA) [3–5] which divides the ion trajectory in successive two-body collisions is the good formalism to perform such estimations. Indeed, it allows to quickly deal with any type of ion irradiation (ion nature and energy) in any material. The limitations of such BCA approaches are well-known. For instance, thanks to molecular dynamics (MD) simulations [6,7] and experiments [8], it has been known for decades that BCA codes overestimate the number of created defects by primary damage. Moreover, they cannot give information about the detailed structure of the clusters of defects formed directly after the collisions cascades. Nevertheless, BCA simulations remain extremely useful because they are simple and fast. The principles of BCA have been described many times in previous works [3–5] and we just recall that BCA uses generic pair-wise interaction potentials and rely intensively on scattering theory. While some rare codes use energy integrals in the BCA framework to calculate average number of collisions and atomic displacements (e.g. the DART code [9]), most of the BCA codes deal with real space trajectories and describe explicitly the sequence of collisions sustained by the incoming ion.
The two major historic codes are SRIM [3,10] and MARLOWE [5]. Marlowe includes a description of the crystalline structure of the materials and because of that, it is more complex than SRIM which is based on a random material assumption. Furthermore, SRIM comes with a graphical user interface, which makes it easy to use. Thus, it has been and remains extensively used as the common tool to estimate primary damage and implantation profiles.
In SRIM, two main types of damage calculation exist: full cascade (FC) and quick calculation (QC). In both modes, the trajectory of the incoming ion through its successive collisions is followed, until its kinetic energy falls below a given threshold where it is stopped. FC mode describes fully the cascades, i.e. the trajectories of all atoms accelerated by the ions or, recursively, by previously accelerated atoms, until they all come to rest (when their kinetic energy falls below the stopping threshold). In QC mode, only the trajectory of the ion is followed. And effective formulas give an estimation of the damage resulting from each collision of the ion (see below). From either mode, one obtains the number of atomic displacements along the trajectory of the ion. From this number and the density, one can deduce the local amount of dpa (displacement per atom).
People have used SRIM for so many years that it has become a sort of reference for the BCA estimation of damage. It is like an unofficial standard. In quite many papers, one may read sentences such as “the damage has been calculated with SRIM” without much or any detail.
While SRIM remains intensively used in the ion irradiation community, it faces a few severe weaknesses. First the actual code is unknown. The only thing one can get from the website is a windows executable and a manual. Back in the 1980s, a listing appeared in a book [3]. This listing does not include all the options that exist in the present SRIM, e.g. it contains only the QC and not the FC mode. A book with additional details appeared in the 1990s [3] (the present manual is a recopy of this book). However, the code listing is not given in this book and some things remain undetailed (see below). The ignorance of what is actually in the code is in unfavourable contrast with present day standard of open source programming. As we shall show below, the inability to look into the details of the code makes it very difficult to reproduce SRIM results. Indeed BCA codes, beyond their apparently simple formalism, rely on some assumptions which, in the case of SRIM are not always documented. Moreover, SRIM code gets more and more difficult to install on computers as years pass by. It seems that the development and updating of this code has been frozen for many years. As will be exemplified below, some interesting recent numerical developments in ion-ion interactions have not been included in the code. For all these reasons, we believe that the ion irradiation community should not rely so much on this ageing and problematic code. Alternatives should be built.
In this context, the requirements a satisfactory alternative must fulfil are three-fold. First, unlike SRIM, the code must be open-source. Second, like SRIM, it must be easy to use for people non-specialized in numerical simulations. Finally, and more strangely, in order to be accepted by the community, an alternative to SRIM must provide results identical or at least very close to the ones of SRIM. Indeed, as mentioned below, SRIM has been used so intensively and for so many years that any code which gives different results, whatever their experimental accuracy and physical correctness will not be adopted by the community. Finally, in the nuclear context, an alternative to SRIM should include the QC of damage, which is very commonly used in this community.
Keeping the objective of providing an alternative to SRIM, we chose to implement QC in the Iradina code [11] originally developed by Christian Borschel and Carsten Ronning from the university of Jena. Compared to the few other modern BCA codes (see below), Iradina has some advantages. First, it is truly open-source. Second being written in C, it is easy to read. Third, it proves very fast. This is because it relies on the formalism implemented originally in the Corteo code [12] which has been developed by François Schiettekatte for ion beam analysis. In this code, the calculation of the scatterings use logarithmically-scaled stopping tables which greatly speeds up the calculation. This formalism is much faster than the one based on the so-called Magic formula implemented in SRIM.
Other modern BCA codes we are aware of include Mytrim [13], SDTrimSP [14] and IM3D [15]. To our knowledge, SDTrimSP is not open-source. From what we understand, MyTrim uses the Magic formula (instead of fast Corteo's formalism) which should make it quite slow. Finally, contrary to what authors claim, IM3D is not open-source. Indeed the transport routines at the heart of this code are included in an executable archive, which one has to download separately. Strangely enough, the input variables of IM3D have almost identical names to the ones of Iradina. Marlowe code has recently be renewed in connection with mixed BCA-MD simulations [16]. But it remains not very user-friendly and much more complex than BCA codes considering random material. It can therefore not be regarded as an alternative to SRIM.
We present in the following, how we realized the implementation of QC in Iradina. We then compare our results with the ones of SRIM. Finally, we discuss QC in non-elemental solids and give our opinion on how to choose between FC and QC calculations.
2 Implementation of QC in Iradina
2.1 Elemental solids
The history of QC of damage dates back to the late 1960s [17,18]. At that time, due to the very limited computer resources available, even the BCA description of a full cascade was challenging, not to mention MD calculations, which were in their infancy [19]. The goal of QC was to estimate the amount of damage created by an accelerated atom of kinetic energy T; the damage being expressed as a number of displaced atoms. In the ion irradiation context, this accelerated atom results from an elastic collision with the incoming ion. With QC formulas, one did not have to describe the full cascade, but only the successive collisions of the ion.
Two steps appear in the QC formalism. First, the kinetic energy T of the accelerated atom must be transformed into the so-called damage energy E. This energy is the portion of T available for ballistic collisions, i.e. the part which is not lost to electrons through inelastic collisions. To do so, one resorts to formulas by Lindhard [20] to estimate the portion of T lost by ballistic losses:
 (1)
(1)
 (2)
(2)
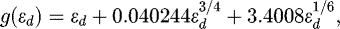 (3)
(3)
 (4)
(4)
In these expressions, Z and M are the atomic number and molar mass of the accelerated atom. Masses and energy are expressed in grams and eV respectively. Note that in FC calculations, electronic losses are accounted for by a slowing term applied to the moving atom between two subsequent collisions and E is the sum of the energy lost through each successive collisions with atoms in the material.
Second, the damage energy must be converted into damage production by a damage formula. Various formulations appeared in the late 1960s and early 1970s [18]. Nowadays, the so-called modified Kinchin-Pease or Norgett-Robinson-Torrens (NRT) [17] formula is used:
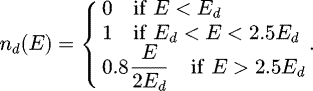 (5)
(5)
We implemented formulas (1) to (5) in Iradina and set up a new simulation type for which the code calculates the trajectory of the sole ion and the damage created by the recoil of each collision by the above formulas. When actual damage is created (nd (E) > 0), the code assigns it entirely to the point where collision took place. The damage is eventually stored in the vacancy file. In QC, one cannot distinguish replacements and interstitial creations. These defects are therefore not counted.
As mentioned before, BCA codes rely on a few physical assumptions which impact the coding algorithms. The determination of the flight path between two successive collisions is one of them. The choice of the flight path is closely related to the possible impact parameters of the collisions. Iradina in its original version [11] include three choices for the free flight path l: a constant flight path set by the user; a constant flight path equal to the interatomic distance; a Poisson distributed flight path with inter-atomic distance as a mean value, the latter being the default. In all cases, the impact parameter is then chosen randomly with an upper maximum impact parameter which is deduced from the flight path as follows. The flight path and the maximum impact parameter can be regarded as the length and radius of a cylinder. The volume of this cylinder is set to the atomic volume:
 (6)
ρ being the atomic density so that 1/ρ is the atomic volume. One then has:
(6)
ρ being the atomic density so that 1/ρ is the atomic volume. One then has:
 (7)
(7)
The actual impact parameter is randomly chosen as:
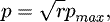 (8)
with r being a random real number between 0 and 1.
(8)
with r being a random real number between 0 and 1.
To reach a better agreement between SRIM and Iradina with QC, we had to implement a new choice of calculation of the free flight path and impact parameter: the so-called impulse approximation. Following [21], one first calculates a maximum impact parameter Pmax, then one deduces the flight path. Pmax is set as the impact parameter corresponding to a given minimum energy transfer Emin. Emin is chosen equal to the energy at which the ion is stopped which is an input choice (reasonable values are around a few eV).
Considering the collision between an ion (M1,Z1) of energy T1 with a target (M2,Z2), one defines successively:
-
the screening length a
 (9)
where a0 = 0.529 Å is the Bohr radius;
(9)
where a0 = 0.529 Å is the Bohr radius;
-
the reduced energy ε
 (10)
(εmin is defined from Emin with the same formula).
(10)
(εmin is defined from Emin with the same formula).
-
and the maximum impact parameter Pmax with
 (11)
(11)
 (12)
(12)
 (13)
(13)
The flight path is then deduced from equation (6) and the actual impact parameter is selected randomly up to Pmax (Eq. (8)).
We tested our implementation of QCs in Iradina on the case of self-irradiation in iron. We calculated irradiation by Fe ions of energy 500 keV or 2 MeV with normal incidence. The damage and implantation profiles calculated with Iradina and SRIM with QCs are given in Figure 1. One can note that for both energies SRIM and Iradina predict very close damage profiles. We obtained similar agreement in the various test cases we performed on elemental solids. Our implementation of QCs is therefore validated for the case of elemental solids.
 |
Fig. 1 Damage profiles for 2 MeV and 500 keV self-irradiation in iron estimated with quick calculation. Comparison between Iradina (solid lines) and SRIM (dashed lines). |
2.5 QC for non-elemental solids
The implementation of QCs for alloys or more generally non-elemental solids is less straightforward. Indeed while, such calculations are possible with SRIM, there is no indication whatsoever on how they are actually performed. The difficulty is easily understood looking at the above formulas (Eqs. (1) to (5)). They depend on the mass (M) and atomic number (Z) of the target atom which is therefore supposed to be also characteristic of the irradiated material. Despite the lack of any information in SRIM documentation, one can deduct from tests in multi-component solids that the QCs in non-elemental solids proceed as follows. For each collision, the nature of the target atom is randomly selected, and the impact factor is chosen (Eqs. (6) to (12)). With the transferred kinetic energy, the damage is then estimated applying formulas (1) to (5) with the mass and atomic number of the target atom, completely neglecting the fact that the material is in fact in a multi-component system. In the following, we present some results of xenon irradiations in UO2. In this case when the incoming ion hits a uranium (resp. oxygen) atom, the formula is applied with M = 238.03 and Z = 92 (respectively M = 16 and Z = 8). We implemented this formulation in Iradina.
The comparison between iradina and SRIM for the UO2 test case is given in Figure 2. One can see that the agreement is good, though not perfect. We could not find any way to improve the agreement between Iradina and SRIM. We contemplated other possibilities namely, applying the formulas to an arithmetical or geometrical average atom with M and Z given as composition averages of the M and Z of the components. These other formulations result in damage creation which deviates largely from SRIM results. This is a situation where not knowing how SRIM is actually coded proves very inconvenient and makes it impossible to reproduce its results with another code. Anyway, we believe the slight discrepancy between SRIM and Iradina for QCs in non-elemental solids is rather inconsequential. Indeed, as we shall discuss below, such calculations are unsuitable for these materials.
 |
Fig. 2 Damage profile for xenon irradiation in UO2 estimated with quick calculation. Comparison between Iradina (solid lines) and SRIM (dashed lines). |
2.6 Iradina as an alternative to SRIM
With the above-described implementation, we achieved correct agreement between SRIM and Iradina for QCs. The agreement between SRIM and Iradina for FC calculations was already highlighted in the original Iradina paper [11]. We checked it for our test cases and indeed found very close results for Iradina and SRIM. The same is true for the ion implantation profiles. With the present addition, Iradina is now able to reproduce SRIM calculations in the two main damage calculations frameworks: FC and QC.
Being open-source, Iradina therefore fulfils two of the requirements for a satisfactory alternative to SRIM. The last one is to have an easy to use graphical user interface (GUI) for non-experts in simulations. The original Iradina already has a user interface. While this interface is quite elegant and useful, it was not conceived to run SRIM like calculations. Moreover, it is not open source and thus cannot be adapted to such calculations. We therefore preferred to design a new GUI. This GUI is briefly described in Appendix A. Finally, Iradina has recently been made available on source forge [22]. The SRIM-like GUI is also available on source-forge with packages to be used in linux or windows environments to perform SRIM like calculations with the Iradina code embedded in it [23].
3 Choosing between FC and QC
Users of SRIM or Iradina have to choose between two ways of calculating the damage profile in ion-irradiated materials. We want in this section to elaborate on this choice and present our opinion about it. We shall first present some comparisons between these two schemes for elemental or non-elemental solids based on the same test cases we used before. We should compare not only the damage production but the profiles of energy deposition.
3.1 Comparisons
The first thing to realize is that the two damage frameworks give quite different results. This is illustrated in Figures 3–6 in the cases of Fe and UO2. This should be no surprise as the two calculations are based on quite different premises. As explained above, FC describes the complete cascades while QC use formulas (1) to (5) to estimate the damage created by the Primary knocked-on atom (PKA) resulting from each collision of the ion.
Focusing for now on mono-elemental solids, one can note that QC tend to predict smaller amounts of defects than FC (Fig. 3). It is worth stressing that the ratio between QC and FC depends on the material and irradiation under study. For instance, it is around 0.5 for self-irradiation in iron and closer to 0.7 for self-irradiation in aluminium (not shown). Thus, one cannot deduce what FC results would be from QC calculations (and the other way around). As described in equations (1) to (4), QC rely on an assumed division of the kinetic energy of the PKA into electronic and ballistic losses in the material. The validity of this division can be checked by comparisons with FC calculations. Figure 4 presents, for each framework, the two types of energy deposition as a function of depth, in the case of 500 keV and 2 MeV self-irradiation in iron. One can note that Robinson formulas perform rather well. The electronic losses are however slightly overestimated especially at low energy. Another difference appears pertaining to the localization of energy losses. In FC, the calculated cascades have some spread which dispatch the energy losses in the volume of the material. At the opposite, in QC, the energy deposition of an (implicit) cascade is located at the position of the corresponding collision with the incoming ion, neglecting its spread. The energy deposition due to the first collisions of the ions which happen close to the surface are then staked at the lowest depths. This is especially visible at low energy (left panel of Fig. 4).
QC thus perform reasonably well for elemental solids. Considering Figures 5 and 6, it appears readily that the differences between FC and QC are more striking for non-elemental solids. At first, considering the global defect production (Fig. 5), one obtains the same kind of difference between FC and QC that appeared for elemental solids. However, the material being made of multiple species, one can also consider the amount of vacancies created for each species. In the case of UO2, one then sees that the ratio of created vacancies for each species (U and O) is very different for FC and QC. It appears clearly that the distribution of damage between O and U is unphysical for QC. Indeed, QC predicts that the majority of vacancies are of the uranium type. Even considering the differences in collision cross-sections, this contradicts the fact that there are twice as many oxygen atom than uranium and that their displacement energy is two times smaller.
Another problem with QC for multi-component materials appears for the energy losses. Figure 6 clearly shows that QC and FC are in strong disagreement for the balance between electronic and ballistic energy depositions. This is especially a problem when one want to study the relative or synergistic effects of electronic over ballistic losses. Ratios of energy depositions calculated with QC are then utterly wrong.
Using QC instead of FC for non-elemental solids thus induces large errors in the distributions of created defects and energy losses compared to FC calculations. Applying QC for such systems is therefore very questionable. These discrepancies are naturally related to the application of mono-elemental formula for each component of the materials after each collision. This assumption is obviously un-physical.
One may wonder why such an approximation was coded in SRIM in the first place. The reason may be related to the NRT calculation of damage in neutronics codes. Indeed neutron transport and reaction codes such as Tripoli [24] or NJOY [25] are primarily concerned with the fate of the neutrons through interactions with atoms of the materials. They consider series of nuclear reactions or elastic collisions of a neutron with atoms. The amount of damage created by the result of a nuclear reaction or an elastic collisions are secondary outputs of the neutron code irrelevant for the main calculation. Because such codes consider interactions with one atom at a time, the damage formulas depend on the sole nature of the atom interacting with the neutron. Physically, this is as wrong as in ion irradiation codes, but the consequences for neutronics are zero. Indeed, damage productions being simple pieces of information, they do not affect the fate of the neutrons which is the actual object of neutronics codes. One may suppose that NRT formulas were implemented in neutron codes, and then simultaneously introduced in SRIM for consistency with these codes even for multi-component systems where they are physically irrelevant.
 |
Fig. 3 Damage profiles for 2 MeV and 500 keV self-irradiation in iron calculated with Iradina for quick calculation (solid lines) and full cascade (dashed lines). |
 |
Fig. 4 Energy deposition for 500 keV and 2 MeV self-irradiation in iron. |
 |
Fig. 5 Damage profiles for 300 keV and 1 MeV Xe irradiation in UO2 calculated with Iradina for quick calculation (solid lines) and full cascade (dashed lines). Black, red and blue curves are the total, uranium and oxygen vacancy production respectively. |
 |
Fig. 6 Energy deposition for 300 keV Xe irradiation in UO2. |
3.2 Choice between QC and FC
As explained above, FC is more physically grounded than QC. It may seem that FC should therefore always be preferred. Nevertheless, a few reasons have been put forward to prefer QC over FC. We review them briefly. The most basic one is that in SRIM, FC calculations are extremely slow and QC are better suited to quickly estimate the damage. This practical argument does not apply to Iradina where both QC and FC are very fast (Iradina is actually about two orders of magnitude faster than SRIM). Another questionable argument is the fact that QC tend to be somewhat closer to the MD predictions than FC calculations. But QC results still deviates strongly from MD. At high PKA energies, there is an overestimation of about 3 for the number of defects with QC in iron [26] (the factor is thus about 6 for FC). Thus, one cannot say that the agreement is between QC and MD is good (see also below the discussion about arc-dpa).
More profound arguments have been put forward by Stoller et al. [27]. The conclusion of their work “On the use of SRIM for computing radiation damage exposure” is three-fold:
-
it is not possible to determine the “right” number of displacements generated by a given PKA in any absolute sense. MD simulations provide the most realistic estimate, but MD results are also model;
-
authors should fully describe how they have calculated any dpa values they report and endeavour to determine how the dpa were calculated in any previous experiments to which they compare their own data;
-
QC is to be preferred because of its consistency with the NRT standard and previous publications.
We fully agree with the first two conclusions. One could never overstress that models are just models, even the most up to date of them. In the same way, one should always state precisely how damage and dpa are calculated (which damage formalism, Ed, etc.). As exemplified above, stating a number of dpa without specifying the details of how they were calculated caries little information.
Nevertheless, we respectfully tend to qualify or moderate the last conclusion about favouring QC over FC. It is true that, as far as elemental solids are concerned, there are some benefits to use QCs. The consistency with the NRT standard is naturally the main one. It allows direct comparison of dpa levels between ion and neutron irradiations. There are therefore legitimate reasons to favour QC over FC for elemental solids when quantitative comparisons damage estimated from neutronics codes are planned. In our opinion, the situation is quite different for multi-component solids. For such materials, QC are physically and qualitatively wrong. The distribution of atomic displacements among the various atomic species as well as the division between electronic and ballistic energy deposition are basically just non-sense with this framework. We therefore believe QC should not be used for such materials. Two things tend to confirm that the designer of SRIM felt the same way. First, nothing appears in the manual about QC in non-elemental materials. Second, looking at the outputs of QC of SRIM, one can realize that the number of created vacancies in QC calculations is not broken down into species but given as the whole. Both points indicate that these calculations were intended only for pure solids. The reason why they were enabled for multi-component materials remains unknown. We contemplated disabling QC for alloys in Iradina, but we chose not to forbid this use of the code, mainly for consistency with what one can do with SRIM. Coming back to Stoller et al. [27], one can note that they deal only with pure solids in their paper, also consistently with implicitly restricting QC to mono-elemental solids.
Finally, we would advise to favour FC over QC in all cases because it more grounded physically and applicable to all materials. QC remains a good option for pure solids in the case of actual quantitative comparisons with neutron irradiations in which damage levels are estimated with the NRT formulas. Consistency with previous studies may also be a reason to give QC damage levels. One may even contemplate using QC in multi-component systems in such particular situations, but we would then highly recommend to give also FC results. The same should be done for elemental solids when one plans to compare between pure or alloyed materials at some point of the study.
As mentioned above, the NRT formula is known the overestimate the damage creation compared to MD. One route of improvement would be to modify the NRT formula (Eq. (5)) and QC to better fit with the actual creation or MD prediction of defects. This is the purpose behind the arc-dpa proposition. The idea is to replace the NRT formula with the so-called arc-dpa formula (arc stands for athermal recombination corrected) [28]. In this formulation, the damage production for kinetic energies larger than 2.5 Ed is rescaled by a factor ξ(E):
 (14)
with
(14)
with
 (15)
(15)
The 0.8 factor is thus replaced by a decreasing function of the PKA energy which starts from 0.8 and converges around 0.3 × 0.8 for iron. This proposition to replace NRT (Eq. (5)) by the arc-dpa (Eqs. (14) and (15)) is still under debate. In our opinion, it faces a couple of issues. First it relies on the existence of MD simulations to fit the additional parameters (b and c) entering the arc-dpa formulas. One then has to face the difficulties and uncertainties of such calculations, e.g. dependence on the empirical potential [29], on the detailed or not inclusion of electronic losses [30], etc. These choices do affect the amount of created defects in a non-negligible way. In view of the continuing activity on cascade simulations even in simple materials, obtaining generally accepted reference MD date is not an easy task. Second, there seems to be some pure materials where the arc-dpa formula does not apply, e.g. W [31], where a re-increase of the damage production seems to take place at high PKA energies. In the same way, it has been shown that the arc-dpa formula is not applicable to alloys or multi-elemental solids [32]. Its utility and field of application appears therefore quite restricted. One may however contemplate its implementation as an alternate damage formula replacing NRT in specific cases. There would be no difficulty to do so in Iradina for instance. But then, one would lose the consistency with previous studies or neutronics evaluation based on the NRT formula. To reach a better agreement with actual damage production, one would spoil the main advantage of QC. The situation would naturally change, if the dpa standard was modified which is not the case at present.
4 Conclusion
In this paper, we have presented our implementation of Quick-Calculations in the Iradina code. We obtain a good agreement between Iradina and SRIM for such calculations. We shed light on the weaknesses of QC in the case of non-elemental solids, namely the fact that the damage formulas are applied to supposedly pure elemental solids after each collision of the incoming ion with atoms of the material, thus completely neglecting the multi-component nature of the material. This drastic and unphysical approximation leads to wrong results in terms of the distribution of damage among the different species as well as the division of losses between ballistic and electronic components. We therefore advocate not to use such QC for multi-component solids. For the sake of consistency, we tend to suggest to favour FC also for elemental materials. Noticeable exceptions are situations where actual quantitative comparisons with damage estimated by neutronics codes or previous QC estimations of damage are in order.
For what concerns alternatives to SRIM, Iradina being equipped with QC and a GUI for 1D irradiation (designed to perform SRIM-like calculations), we believe it can provide a fast and safe way to perform BCA calculations for the ion implantation community.
Author contribution statement
Jean-Paul Crocombette coded the quick calculations in Iradina, performed the calculations and wrote the present paper. Christian Van Wambeke programmed the graphical user interface to perform SRIM-like calculations.
Appendix A Iradina graphical user interface
We developed a graphical user interface (Iradina-GUI) to perform 1D (SRIM-like) calculations. The GUI is a set of Python 3.5 script files with QT. It requires a few packages, namely: PyQt5, numpy, matplotlib and pandas. The GUI enables to set-up calculations and run them. It automatically saves the inputs and outputs of Iradina and allows navigating around them. A few basic plots are also possible. Iradina_GUI and the associated Iradina code (Iradina_Code) are available on source forge [23]. This directory is a sub section of the general Iradina source forge project [22] maintained commonly by the present author and the original Iradina team (Christian borchel and Carsten Ronning).
Packages are available for windows and linux, together with installation instructions. For windows, the package contains everything to make the program run, including all the packages mentioned above. For linux, a few basic preliminary steps are necessary to include these packages independently from Iradina. The GUI as well as Iradina code itself are works in progress and they should be enhanced in the forthcoming years. The author welcomes comments and suggestions from users.
References
- G.S. Was, Challenges to the use of ion irradiation for emulating reactor irradiation, J. Mater. Res. 30, 1158 (2015) [CrossRef] [Google Scholar]
- S.J. Zinkle, L.L. Snead, Opportunities and limitations for ion beams in radiation effects studies: bridging critical gaps between charged particle and neutron irradiations, Scripta Mater. 143, 154 (2018) [CrossRef] [Google Scholar]
- J.F. Ziegler, J.P. Biersack, M.D. Ziegler, SRIM − The stopping and range of ions in matter (Ion Implantation Press, 2008) [Google Scholar]
- M. Robinson, The energy dependence of neutron radiation damage in solids, Nucl. Fusion React. 1, 364 (1970) [Google Scholar]
- M.T. Robinson, I.M. Torrens, Computer simulation of atomic displacement cascades in solids in the binary-collision approximation, Phys. Rev. B 9, 5008 (1974) [CrossRef] [Google Scholar]
- R. Averback, R. Benedek, K.L. Merkle, Ion-irradiation studies of the damage function of copper and silver, Phys. Rev. B 18, 4156 (1978) [CrossRef] [Google Scholar]
- M.W. Guinan, J.H. Kinney, Molecular dynamic calculations of energetic displacement cascades, J. Nucl. Mater. 104, 1319 (1981) [CrossRef] [Google Scholar]
- L.E. Rehn, P.R. Okamoto, Production of freely-migrating defects during irradiation, Mater. Sci. Forum 15–18, 985 (1987) [CrossRef] [Google Scholar]
- L. Luneville, D. Simeone, D. Gosset, A new tool to compare neutron and ion irradiation in materials, Nucl. Instrum. Methods Phys. Res. Sect. B 250, 71 (2006) [CrossRef] [Google Scholar]
- J.F. Ziegler, SRIM, www.srim.org [Google Scholar]
- C. Borschel, C. Ronning, Ion beam irradiation of nanostructures − A 3D Monte Carlo simulation code, Nucl. Instrum. Methods Phys. Res. Sect. B 269, 2133 (2011) [CrossRef] [Google Scholar]
- F. Schiettekatte, Fast Monte Carlo for ion beam analysis simulations, Nucl. Instrum. Methods Phys. Res. Sect. B 266, 1880 (2008) [CrossRef] [Google Scholar]
- D. Schwen, MyTrim, https://github.com/idaholab/mytrim [Google Scholar]
- W. Eckstein, et al. SDTrimSP version 5.00, MaxPlanck- Institut für Plasmaphysik, Report 12/08 [Google Scholar]
- Y.G. Li, et al., IM3D: a parallel Monte Carlo code for efficient simulations of primary radiation displacements and damage in 3D geometry, Sci. Rep. 5, 18130 (2015) [CrossRef] [Google Scholar]
- C.J. Ortiz, A combined BCA-MD method with adaptive volume to simulate high-energy atomic-collision cascades in solids under irradiation, Comput. Mater. Sci. 154, 325 (2018) [CrossRef] [Google Scholar]
- M. Norgett, M.T. Robinson, I. Torrens, A proposed method of calculating displacement dose rates, Nucl. Eng. Design 33, 50 (1975) [CrossRef] [Google Scholar]
- M. Robinson, The energy dependence of neutron radiation damage in solids, Nuclear Fusion Reactor Conference (Culham Laboratory, 1969) [Google Scholar]
- J.B. Gibson, et al., Dynam. Radiat. Damage Phys. Rev. 120, 1229 (1960) [Google Scholar]
- J. Lindhard, M. Scharff, H.E. Schiott, Kgl. Dan. Vidensk. Selsk. Mat. −fys. Medd 33, 14 (1963) [Google Scholar]
- J.F. Ziegler, J.P. Biersack, M.D. Ziegler, in SRIM − The stopping and range of ions in matter (Ion Implantation Press, 2008), pp. 7–16 [Google Scholar]
- C. Borschel, et al., Iradina, https://sourceforge.net/projects/iradina/ [Google Scholar]
- C. Van Wambeke, J.P. Crocombette, Iradina_CEA, https://sourceforge.net/projects/iradina/files/Iradina_CEA/ [Google Scholar]
- E. Brun, et al., Tripoli-4®, CEA, EDF and AREVA reference Monte Carlo code, Ann. Nucl. Energy 82, 151 (2015) [CrossRef] [Google Scholar]
- R.E. Macfarlane, D.W. Muir, F.M. Mann, Radiation damage calculations with njoy, J. Nucl. Mater. 123, 1041 (1984) [CrossRef] [Google Scholar]
- R.E. Stoller, The role of cascade energy and temperature in primary defect formation in iron, J. Nucl. Mater. 276, 22 (2000) [CrossRef] [Google Scholar]
- R.E. Stoller, et al., On the use of SRIM for computing radiation damage exposure, Nucl. Instrum. Methods Phys. Res. Sect. B 310, 75 (2013) [CrossRef] [Google Scholar]
- K. Nordlund, et al., Improving atomic displacement and replacement calculations with physically realistic damage models, Nat. Commun. 9, 8 (2018) [CrossRef] [PubMed] [Google Scholar]
- C.S. Becquart, A. Souidi, M. Hou, Relation between the interaction potential, replacement collision sequences, and collision cascade expansion in iron, Phys. Rev. B 66, 134104 (2002) [CrossRef] [Google Scholar]
- E. Zarkadoula, et al., Electronic effects in high-energy radiation damage in iron, J. Phys.: Condens. Matter 26, 085401 (2014) [CrossRef] [Google Scholar]
- W. Setyawan, et al., Displacement cascades and defects annealing in tungsten, Part I Defect Database Mol. Dynam. Simulat. 462, 329 (2015) [Google Scholar]
- J.P. Crocombette, et al., Molecular dynamics simulations of high energy cascade in ordered alloys: defect production and subcascade division, J. Nucl. Mater. 474, 134 (2016) [CrossRef] [Google Scholar]
Cite this article as: Jean-Paul Crocombette, Christian Van Wambeke, Quick calculation of damage for ion irradiation: implementation in Iradina and comparisons to SRIM, EPJ Nuclear Sci. Technol. 5, 7 (2019)
All Figures
 |
Fig. 1 Damage profiles for 2 MeV and 500 keV self-irradiation in iron estimated with quick calculation. Comparison between Iradina (solid lines) and SRIM (dashed lines). |
| In the text | |
 |
Fig. 2 Damage profile for xenon irradiation in UO2 estimated with quick calculation. Comparison between Iradina (solid lines) and SRIM (dashed lines). |
| In the text | |
 |
Fig. 3 Damage profiles for 2 MeV and 500 keV self-irradiation in iron calculated with Iradina for quick calculation (solid lines) and full cascade (dashed lines). |
| In the text | |
 |
Fig. 4 Energy deposition for 500 keV and 2 MeV self-irradiation in iron. |
| In the text | |
 |
Fig. 5 Damage profiles for 300 keV and 1 MeV Xe irradiation in UO2 calculated with Iradina for quick calculation (solid lines) and full cascade (dashed lines). Black, red and blue curves are the total, uranium and oxygen vacancy production respectively. |
| In the text | |
 |
Fig. 6 Energy deposition for 300 keV Xe irradiation in UO2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


