| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
|
|
|---|---|---|
| Article Number | 5 | |
| Number of page(s) | 6 | |
| DOI | https://doi.org/10.1051/epjn/2018001 | |
| Published online | 09 April 2018 | |
https://doi.org/10.1051/epjn/2018001
Regular Article
α-decay half-lives of some nuclei from ground state to ground state using different nuclear potential
1
Akre Computer Institute Ministry of Education,
Kurdistan, Iraq
2
Becquereal Institute for Radiation Research and Measurements,
Erbil,
Kurdistan, Iraq
* e-mail: akrawy85@gmail.com
Received:
12
July
2017
Received in final form:
19
November
2017
Accepted:
16
January
2018
Published online: 9 April 2018
Theoretical α-decay half-lives of some nuclei from ground state to ground state are calculated using different nuclear potential model including Coulomb proximity potential (CPPM), Royer proximity potential and Broglia and Winther 1991. The calculated values comparing with experimental data, it is observed that the CPPM model is in good agreement with the experimental data.
© D.T. Akrawy, published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
George Gamow interpreted the theory of alpha decay in terms of the quantum tunneling from the potential well of the nucleus [1]. There are many theoretical schemes that used to define α cluster radioactivity and alpha-like models using various ideas such as the ground-state energy, nuclear spin and parity, nuclear deformation and shell effects [2–14]. Frequently used models include the fission-like [15], generalized liquid drop [16], generalized density dependent cluster [17], unified model for α decay and α capture [18], Coulomb and proximity potential [19] and unified fission [20]. These models, with their own merits and failures, have been in acceptable agreement with the experimental data [21,22]. Spontaneous fission and cluster radioactivity were studied in 1980 by Sandulescu, Poenaru, and Greiner [23] based on the quantum mechanical fragmentation theory. Rose and Jones experimentally observed the radioactive decay of 223Ra by emitting 14C in mid 1980s [24,25]. Recently, the concept of heavy-particle radioactivity is further explored by Poenaru et al. [26]. Hassanabadi et al. considered the alpha-decay half-lives for the even–even nuclei from 178Po to 238U and derived the decay constant [27]. Also the half-life for the emission of various clusters from even–even isotopes of barium in the ground and excited states were studied using the Coulomb and proximity potential model by Santhosh et al. [28]. Also, there are many efficient and useful empirical formulas to calculate alpha decay half-lives which are given in reference [29–32]. In this study we used three different nuclear potential including Coulomb proximity potential (CPPM), Royer proximity potential (RPP) and Broglia and Winther 1991 model (BW91). From those models we calculated alpha decay half-lives for 57 nuclei that have Z = 67–91, from ground state to ground state, the root mean square (RMS) deviation was evaluated, and the results are compared with experimental data.
2 Formalism of α-decay
According to one dimensional WKB approximation, the barrier penetration P is given by [33],
 where a, b are tunneling point of integral which are given as V(a) = V(b) = Q. The interaction potential for two spherical nuclei is given by [34],
where a, b are tunneling point of integral which are given as V(a) = V(b) = Q. The interaction potential for two spherical nuclei is given by [34],
 (2)where the first term represents the Coulomb potential with Z1 and Z2 are the atomic numbers of parent and daughter nuclei, the second term is nuclear potential and the final term is centrifugal potential which dependent on the angular momentum ℓ, and reduced mass of nuclei µ. The half-life of alpha decay can be calculated as [35]
(2)where the first term represents the Coulomb potential with Z1 and Z2 are the atomic numbers of parent and daughter nuclei, the second term is nuclear potential and the final term is centrifugal potential which dependent on the angular momentum ℓ, and reduced mass of nuclei µ. The half-life of alpha decay can be calculated as [35]
 (3)where
(3)where  , is frequency of collision with barrier per second, E is the empirical vibration energy, is given as [36]
, is frequency of collision with barrier per second, E is the empirical vibration energy, is given as [36]
 (4)where Q is the energy released [37], and A2 the mass number of α-particle. By substitution value of E and P in equation (3) determines the half-lives.
(4)where Q is the energy released [37], and A2 the mass number of α-particle. By substitution value of E and P in equation (3) determines the half-lives.
In this section, we present the details of three nuclear potential models used for the calculation of α-decay half-lives. When two surfaces approach each other within a distance of 2–3 fm, additional force due to the proximity of the surface is labeled as proximity potential [38]. In this section we discuss each model in details.
2.1 Coulomb and proximity potential model (CPPM)
The proximity potential is considered as [39],
 (5)
where Z1 and Z2 are the atomic numbers of parent and daughter nuclei, z is the distance between the near surfaces of the fragments, and the nuclear surface tension coefficient is given as,
(5)
where Z1 and Z2 are the atomic numbers of parent and daughter nuclei, z is the distance between the near surfaces of the fragments, and the nuclear surface tension coefficient is given as,
 (6)where A, Z and N represent mass, proton and neutron numbers of parent nuclei, respectively, and r is the distance between fragment centers and is given as r = z + C1 + C2, and C1, C2 are the Susmann central radii of fragments are given as:
(6)where A, Z and N represent mass, proton and neutron numbers of parent nuclei, respectively, and r is the distance between fragment centers and is given as r = z + C1 + C2, and C1, C2 are the Susmann central radii of fragments are given as:
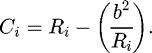 (7)
(7)
ϕ is the universal proximity potential which is given by [40]
 (8)
(8)
 (9)
where ϵ = z/b, is the overlap distance in unit of b where the width of the nuclear surface b ≈ 1 fm.
(9)
where ϵ = z/b, is the overlap distance in unit of b where the width of the nuclear surface b ≈ 1 fm.
The semi-empirical formula for Ri in term of mass number is given as [41],
 (10)
(10)
2.2 Royer proximity potential model (RPPM)
For the α emission where the proximity energy between the two separated α particle and daughter nucleus plays the central role a very accurate formula has been obtained as [42]
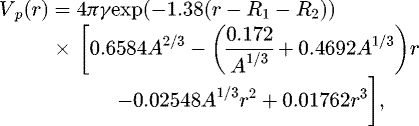 (11)
where A is the mass of the parent nucleus and r the mass-center distance.
(11)
where A is the mass of the parent nucleus and r the mass-center distance.
2.3 Broglia and Winther 1991 model (BW91)
Broglia and Winther derived a refined version of the BW91 potential by taking Wood-saxon potential with dependent condition of being appropriate with the value of the maximum nuclear force which is predicted by proximity potential model. This model reduced in [38,43]
 (12)
(12)
 (13)
here a = 0.63 fm and
(13)
here a = 0.63 fm and
 (14)
(14)
Here the radius Ri has the form
 (15)
(15)
The surface energy coefficient γ has the form
 (16)
where A, Z, and N are the total number for (p, d) parent and daughter, respectively, γ0 = 0.95 Mev/fm2 and ks = 1.8.
(16)
where A, Z, and N are the total number for (p, d) parent and daughter, respectively, γ0 = 0.95 Mev/fm2 and ks = 1.8.
3 Results and discussion
The α-decay half-lives provided by the above nuclear potential models are presented in Table 1 which included CPPM, Royer proximity potential and BW91. The angular momentum l loaded by α-decay from ground state to ground state transition and obeys by the spin-parity selection rule [44]
 (17)
where Δj = |jp − jd|, jp, πp and jd, πd are the spin and parity value of parent and daughter, respectively. The relative superiority of the present choice of the potential can be as well seen in the in Table 1 where our results are reported for different potential models. The outcome of our study is presented in Figures 1–3. In Figure 1 to provide best view of the results, we have plotted logarithm α-decay half-lives including CPPM, RPP, BW91 and experimental data vs. neutron number of parent nuclei, the figures shows the increasing disposal of logarithm half-live for decreasing neutron number of parent nuclei, also this figure refer the three models are more close to experimental data, which indicates to the agreeable of the results. The ΔT parameter is determined, which is representing the different between experimental half-live to theoretical, and reported in Figure 2; which indicated the ΔT of more isotopes is less than one; it seems that the results are more close to experimental data. We predict that the nuclei with higher neutron number a larger half-life and thence more stable. Figure 3 describes the relation between logarithm α-decay half-lives vs. Q-value, it shown that the logarithm α-decay decreases when Q-value increases; it is in agreement with a larger Q-value increases the instability. We calculated the RMS deviation which is defined as [45]
(17)
where Δj = |jp − jd|, jp, πp and jd, πd are the spin and parity value of parent and daughter, respectively. The relative superiority of the present choice of the potential can be as well seen in the in Table 1 where our results are reported for different potential models. The outcome of our study is presented in Figures 1–3. In Figure 1 to provide best view of the results, we have plotted logarithm α-decay half-lives including CPPM, RPP, BW91 and experimental data vs. neutron number of parent nuclei, the figures shows the increasing disposal of logarithm half-live for decreasing neutron number of parent nuclei, also this figure refer the three models are more close to experimental data, which indicates to the agreeable of the results. The ΔT parameter is determined, which is representing the different between experimental half-live to theoretical, and reported in Figure 2; which indicated the ΔT of more isotopes is less than one; it seems that the results are more close to experimental data. We predict that the nuclei with higher neutron number a larger half-life and thence more stable. Figure 3 describes the relation between logarithm α-decay half-lives vs. Q-value, it shown that the logarithm α-decay decreases when Q-value increases; it is in agreement with a larger Q-value increases the instability. We calculated the RMS deviation which is defined as [45]
 (18)for present models which reported in Table 2; which indicate the CPPM model is best model to calculate α-decay half-life comparative with RPP and BW91 models.
(18)for present models which reported in Table 2; which indicate the CPPM model is best model to calculate α-decay half-life comparative with RPP and BW91 models.
Comparative study of α-decay half-lives using three nuclear potential models included CPPM, RPPM and BW91.
 |
Fig. 1 Logarithm α-decay half-live for CPPM, RPP, BW91 and experimental data vs. neutron number. |
 |
Fig. 2 Logarithm α-decay half-live for CPPM, RPP, and BW91 vs. neutron number. |
 |
Fig. 3 ΔT vs. neutron number. |
RMS deviation for CPPM, RPP and BW91 nuclear potential model.
4 Conclusion
Three different nuclear potential are used to calculate the α-decay half-lives for some nuclei from ground state to ground state including CPPM, RPP and BW91. The angular momentums are taken into account. RMS deviations are calculated, it shows that the best nuclear potential is CPPM. The results are compared with experimental data; this comparison provides a reference how to select nuclear potential to calculate α-decay half-lives.
References
- G. Gamow, Z. Phys. 51, 204 (1928) [NASA ADS] [CrossRef] [Google Scholar]
- Z. Ren, G. Xu, Phys. Rev. C 36, 456 (1987) [Google Scholar]
- H. Horiuchi, Nucl. Phys. A 522, 257 (1991) [CrossRef] [Google Scholar]
- R.B. Firestone, V.S. Shirley, C.M. Baglin, S.Y. Frank Chu, J. Zipkin, Table of Isotopes, 8th edn. (Wiley–Interscience, New York, 1996) [Google Scholar]
- R.G. Lovas, R.J. Liotta, A. Insolia, K. Varga, D.S. Delion, Phys. Rep. 294, 265 (1998) [CrossRef] [Google Scholar]
- F. Garcia, O. Rodriguez, M. Gonçalves, S.B. Duarte, O.A.P. Tavares, F. Guzman, J. Phys. G 26, 755 (2000) [CrossRef] [Google Scholar]
- J. Tang, Z.M. Niu, J.Y Guo, Chin. Phys. C 40, 074102 (2016) [CrossRef] [Google Scholar]
- T.N. Ginter et al., Phys. Rev. C 67, 064609 (2003) [CrossRef] [Google Scholar]
- P.E. Hodgson, E. Betak, Phys. Rep. 374, 1 (2003) [CrossRef] [Google Scholar]
- R.D. Herzberg, J. Phys. G 30, 123 (2004) [Google Scholar]
- Z.G. Gan et al., Eur. Phys. J. A 20, 385 (2004) [CrossRef] [EDP Sciences] [Google Scholar]
- D. Seweryniak et al., Phys. Rev. C 73, 061301 (2006) [CrossRef] [Google Scholar]
- A.P. Leppanen et al., Phys. Rev. C 75, 054307 (2007) [CrossRef] [Google Scholar]
- G. Royer, R.K. Gupta, V.Y. Denisov, Nucl. Phys. A 632, 275 (1998) [CrossRef] [Google Scholar]
- J. Dong, H. Zhang, Y. Wang, W. Zuo, J. Li, Nucl. Phys. A 832, 198 (2010) [CrossRef] [Google Scholar]
- D. Ni, R. Zhong-zhou, J. Phys. G: Nucl. Part. Phys. 37, 035104 (2010) [CrossRef] [Google Scholar]
- V.Yu. Denisov, A.A. Khudenko, Phys. Rev. C 80, 034603 (2009) [CrossRef] [Google Scholar]
- K.P. Santhosh, A. Joseph, Pramana J. Phys. 58, 611 (2002) [CrossRef] [Google Scholar]
- J. Dong et al., Chin. Phys. C 34, 182, (2010) [CrossRef] [Google Scholar]
- S. Peltonen, D.S. Delion, J. Suhonen, Phys. Rev. C 78, 034608 (2008) [CrossRef] [Google Scholar]
- D. Ni, Z. Ren, Phys. Rev. C 80, 051303 (2009) [CrossRef] [Google Scholar]
- K.P. Santhosh, J.G. Joseph, S. Sahadevan, Phys. Rev. C 82, 064605 (2010) [CrossRef] [Google Scholar]
- A. Sandulescu, D.N. Poenaru, W. Greiner, Sov. J. Part. Nucl. 11, 528 (1980) [Google Scholar]
- H.J. Rose, G.A. Jones, Nature (London) 307, 245 (1984) [CrossRef] [Google Scholar]
- R. Kumar, M.K. Sharma, Phys. Rev. C 85, 054612 (2012) [CrossRef] [Google Scholar]
- D.N. Poenaru, R.A. Gherghescu, W. Greiner, Phys. Rev. Lett. 107, 062503 (2011) [CrossRef] [PubMed] [Google Scholar]
- H. Hassanabadi, E. Javadimanesh, S. Zarrinkamar, Nucl. Phys. A 906, 84 (2013) [CrossRef] [Google Scholar]
- K.P. Santhosh, P.V. Subha, B. Priyanka, Pramana J. Phys. 86, 819 (2016) [CrossRef] [Google Scholar]
- D.T. Akrawy, D.N. Poenaru, J. Phys. G: Nucl. Part. Phys. 44, 105105 (2017) [CrossRef] [Google Scholar]
- S. Zhang, Y. Zhang, J. Cui, Y. Wang, Phys. Rev. C 95, 014311 (2017) [CrossRef] [Google Scholar]
- V.Y. Denisov, O.I. Davidovskaya, I.Y. Sedykh, Phys. Rev. C 92, 014602 (2015) [CrossRef] [Google Scholar]
- G. Royer, R.K. Gupta, V.Y. Denisov, Nucl. Phys. A 848, 279 (2010) [CrossRef] [Google Scholar]
- K.P. Santhosh, R.K. Biju, S. Sahadevan, J. Phys. G: Nucl. Part. Phys. 36, 115101 (2009) [CrossRef] [Google Scholar]
- K.P. Santhosh, R.K. Biju, J. Phys. G: Nucl. Part. Phys. 36, 015107 (2009) [CrossRef] [Google Scholar]
- K.P. Santhosh, J.G. Joseph, B. Prlyanka, S. Sahadevan, J. Phys. G: Nucl. Part. Phys. 38, 075101 (2011) [CrossRef] [Google Scholar]
- K.P. Santhosh, J.G. Joseph, B. Prlyanka, J. Phys. G: Nucl. Part. Phys. 39, 085106 (2012) [CrossRef] [Google Scholar]
- E. Javadimanesh, H. Hassanabadi, A.A. Rajabi, H. Rahomov, S. Zarrinkamar, Commun. Theor. Phys. 58, 146 (2012) [CrossRef] [Google Scholar]
- I. Dutt, R.K. Puri, Phys. Rev. C 81, 064609 (2010) [CrossRef] [Google Scholar]
- K.P. Santhosh, I. Sukumaran, B. Prlyanka, Nucl. Phys. A 935, 28 (2015) [CrossRef] [Google Scholar]
- K.P. Santhosh, B. Prlyanka, Nucl. Phys. A 929, 20 (2014) [CrossRef] [Google Scholar]
- K.P. Santhosh, S. Sahadevan, Nucl. Phys. A 847, 42 (2010) [CrossRef] [Google Scholar]
- R. Moustabchir, G. Royer, Nucl. Phys. A 683, 266 (2001) [CrossRef] [Google Scholar]
- W. Reisdorf, J. Phys. G: Nucl. Part. Phys. 20, 1297 (1994) [CrossRef] [EDP Sciences] [Google Scholar]
- V.Y. Denisov, A.A. Khudenko, At. Data Nucl. Data Tables 95, 815 (2009) [CrossRef] [Google Scholar]
- Y. Qian, Z. Ren, D. Ni, Phys. Rev. C 83, 044317 (2011) [CrossRef] [Google Scholar]
Cite this article as: Dashty T. Akrawy, α-decay half-lives of some nuclei from ground state to ground state using different nuclear potential, EPJ Nuclear Sci. Technol. 4, 5 (2018)
All Tables
Comparative study of α-decay half-lives using three nuclear potential models included CPPM, RPPM and BW91.
All Figures
 |
Fig. 1 Logarithm α-decay half-live for CPPM, RPP, BW91 and experimental data vs. neutron number. |
| In the text | |
 |
Fig. 2 Logarithm α-decay half-live for CPPM, RPP, and BW91 vs. neutron number. |
| In the text | |
 |
Fig. 3 ΔT vs. neutron number. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


