| Issue |
EPJ Nuclear Sci. Technol.
Volume 3, 2017
|
|
|---|---|---|
| Article Number | 10 | |
| Number of page(s) | 5 | |
| DOI | https://doi.org/10.1051/epjn/e2015-50012-0 | |
| Published online | 03 April 2017 | |
https://doi.org/10.1051/epjn/e2015-50012-0
Regular Article
The role of power sources in the European electricity mix
1
Commissariat à l’Énergie Atomique et aux Énergies Alternatives, Direction de l’Énergie Nucléaire, CEA Saclay, Bât. 121, 91191 Gif-sur-Yvette cedex, France
2
PHELMA/Grenoble INP and LPSC/IN2P3/CNRS, 53 rue des Martyrs, 38026 Grenoble cedex, France
3
Institut de Radioprotection et de Sûreté Nucléaire, 31 avenue de la Division Leclerc, 92262 Fontenay-aux-Roses, France
4
Laboratoire des Sciences du Climat et de l’Environnement, L’Orme des Merisiers, 91191 Gif-sur-Yvette cedex, France
* e-mail: bernard.bonin@cea.fr
Received:
3
May
2015
Accepted:
13
November
2015
Published online: 3 April 2017
The ongoing debate in Europe about energy transition enhances the necessity to evaluate the performance of the envisaged mix of power sources, in terms of production cost, CO2 emissions and security of supply. In this study, we use MIXOPTIM, a Monte-Carlo simulator of the behavior of a mix of power sources on a territory, to evaluate the performance of the present EU power mix. After a validation on the French mix, we applied it to the whole EU territory and made variational calculations around the present mix to evaluate the performance impacts induced by small changes in installed renewable power and nuclear power. According to the analyzed criteria, the study shows that a plausible way to keep an affordable MWh in Europe with minimal amount of CO2 emissions and acceptable security of supply could be to extend the life of existing Gen II nuclear reactors. All other options lead to the degradation of the mix performance, on at least one of the three criteria listed above.
© B. Bonin et al., published by EDP Sciences, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The ongoing debate in Europe about energy transition gave rise to many scenarios about the evolution of the EU power mix. It is necessary to evaluate the performance of the mix in these scenarios, in terms of cost of electricity, CO2 emission and security of supply. In the present paper, our ambition is not to study a complete scenario extending over the future decades. We limit our analysis to the near-term future, and explore the consequences of small changes in the composition of the mix. For this purpose, we use MIXOPTIM [1], a Monte-Carlo simulator of the behavior of an electricity mix of power sources on a territory, to evaluate the performance of the present European power mix, and indicate how these performance indicators would evolve under an elementary change in the composition of the source mix. Despite its simplicity, we believe that this evaluation can be a useful guide to understand the value and consequences of the policy decisions associated with the energy transition.
2 Principle of the MIXOPTIM simulation
The evaluation of the cost of an electricity mix is not as simple as it might appear at first sight. Several factors introduce complications in the system. Firstly, electricity cannot be stored in large amounts at the present time, and the demand, which fluctuates, must be met exactly and at all times by providing sources. Secondly, these sources are called upon in a specific order, within the limits of their availability. Thirdly, this availability itself is variable, especially for renewable sources like wind or solar energy, which take an increasing share in the mixes in Western countries. Moreover, the capacity of interconnexion between territories is growing, thus giving an increasing importance to imported and exported power fluxes (with wildly fluctuating prices). The conjunction of these four factors suggests a rather non-linear behavior of the system, and a priori hampers a simple determination of average values for cost evaluation.
The classical approach based on the use of averaged load factors is not fully satisfactory because it is not self-consistent: it uses load factors as input data while they should in principle be considered as output data, since they depend on the energy mix.
Some authors have treated this problem by simulating the behavior of the mix on a time-dependent basis, using the hourly chronicles of the demand over past years [2]. Another plausible, almost equivalent approach is to use the Monte-Carlo method, which is well suited to treat complicated physical systems. The Monte-Carlo simulation gives access to the whole phase space, as opposed to time-dependent approaches using hourly chronicles. It has the advantage of being fully self-consistent and potentially independent of the chronicles of past years, thus allowing extrapolation studies on hypothetic future mixes with completely different composition of power sources and demand.
In the MIXOPTIM simulation, the territory is equipped with power sources of various kinds, e.g. wind, solar, hydraulic sources, etc. The availability of the sources at any given time t is treated as a random variable, to take into account the fluctuations of sun, wind, and, more generally, the availability of all sources. The demand is also treated as a random variable to take into account the fluctuating nature of the demand. The power demand can be met by the power sources existing on the territory, or by imports from outside. A sampling of these random variables corresponds to a particular situation of the mix, for which the sources are solicited in a pre-defined ranking order, to fulfill the power demand. For this situation of the mix at time t, the hourly cost of the electricity, the hourly amount of CO2 emitted, the amount of power exported or imported from outside can be calculated. Average values of these quantities are then calculated after many samplings of the random variables. The MIXOPTIM simulation also enables one to calculate the probability of a power cut, e.g. the occurrence of the event where the power demand cannot be satisfied by an undersized power mix.
MIXOPTIM is an open-access software, which is available on http://www.mixoptim.org. Details on the model have been described in a previous paper [1].
3 Input data for the scenarios simulation
MIXOPTIM needs the following input data:
-
the cost of the MWh for each production source has been split into a variable component, proportional to the produced power, and a fixed component, proportional to the installed power. The fixed component corresponds mainly to the amortization of the investment. The cost structure of the sources has been taken from reference [3]. Gen II and Gen III nuclear power plants are treated separately because of their very different cost structure;
-
the CO2 emission of the sources has also been split into a fixed and a variable component; the fixed part takes into account the whole life cycle of the power production source [4], including the CO2 produced during its construction;
-
the probability law for the demand has been deduced from the hourly chronicles of the demand over past years, available in reference [5];
-
in the same way, probability laws for the availability of the sources have been obtained from the hourly chronicles of the production (for the mandatory sources, wind and sun, the availability factor equals the production factor since all the available sources are actually used). Since no aggregated data exists at the European level, we considered the French hourly chronicle (available from Ref. [5]) to derive the probability laws of the sources. As will be shown later in the text (Tab. 2), the reasonable agreement between the observed and calculated load factors of the sources (especially wind and sun) confirms that this approximation does not introduce important bias in the results;
-
the composition of the European power mix has been taken from reference [6] (Tab. 1).
4 Validation of MIXOPTIM
The results of MIXOPTIM have been validated by comparison with the observed performance of the 2011 French mix [1] (Tab. 2).
The agreement between the observed and calculated results suggests that the MIXOPTIM simulation is able to give reasonably precise and accurate information on a mix.
Another piece of validation of MIXOPTIM can also be found in the analysis of load factors of the sources in the European mix: the load factors Kp observed for the sources in 2013 are correctly reproduced by MIXOPTIM at the European scale (Tab. 3).
This validation exercise has also highlighted that the quality of the results depends more on the quality and consistency of the input data than on the simulation tool itself. Traceability of the data used as input is crucial!
The validation of MIXOPTIM on the French and European mixes being satisfactory, we use confidently the tool to perform trends and sensitivity studies on the European mix.
Comparison between the observed and calculated load factors of the sources for the 2013 EU power mix.
5 Sensitivity of the performance of the mix to small changes in its composition
Three performance criteria can be calculated with MIXOPTIM:
-
an economic performance indicator of the mix, defined as the average cost
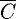 of the MWh, divided by the average power demand:
of the MWh, divided by the average power demand: 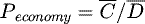 , expressed in €/MWh;
, expressed in €/MWh; -
the CO2 emissions of the mix, defined as the average CO2 emissions divided by the average power demand:
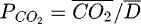 , expressed in kilograms of CO2/MWh;
, expressed in kilograms of CO2/MWh; -
the probability of occurrence of a power cut Pcut at any time t is also provided by the MIXOPTIM software.
In this first sensitivity study, these three criteria were calculated for the 2013 EU mix (taken as a reference), and for mixes modified by the addition of 20 GW of installed power for a given power source (Tab. 4 and 5). The addition of 20 GW was made separately and successively for each power source, and the performance indicators of the modified mix were calculated with MIXOPTIM.
The results of the addition of 20 GW of installed power in wind, solar PV, hydraulic, etc. sources are summarized in Table 5.
The choice of an increment of 20 MW results from a compromise between the precision of the Monte-Carlo calculation, and the need to avoid non-linear effects that would arise in the mix for an exceedingly large increment in installed power. The statistical precision of the Monte-Carlo calculation is ±0.01 €/MWh on the cost, ±0.01 kgCO2/MWh on the CO2 emission, and ±2 × 10–5 on the power cut probability.
It can be seen from Table 5 that the addition of installed power increases the cost of the MWh for all sources, except for nuclear Gen II. In this special case, since the European fleet of Gen II reactors can only decrease, one should rather consider that a reduction of the Gen II installed power would result in an increase of the cost of the MWh.
The CO2 emissions of the mix increase or decrease according to whether the considered source is low carbon or not. It also depends on the value of the load factor Kp of the source.
Of course, the addition of installed power reduces the probability of a cut, more efficiently if the source is controllable, less efficiently if it is intermittent. The increase of the cost of the MWh mentioned above can be seen as the cost of the insurance against power cuts.
A global dimensionless figure of merit Pglobal of the mix performance can be constructed, as a weighted sum of the normalized criteria defined above:
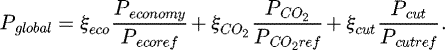
This global figure of merit gives an estimate of the mix performance compared to the performance of the reference mix. The values chosen in this paper for the weighting coefficients are ξeco = 0.8, 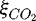 = 0.1, ξcut = 0.05. These values reflect only the subjective view of the authors on the relative importance of the three performance criteria of the mix. This choice can be viewed as the attribution of an economic value to an avoided ton of CO2, and to an avoided yearly hour of power cut.
= 0.1, ξcut = 0.05. These values reflect only the subjective view of the authors on the relative importance of the three performance criteria of the mix. This choice can be viewed as the attribution of an economic value to an avoided ton of CO2, and to an avoided yearly hour of power cut.
Value of an avoided ton of CO2:
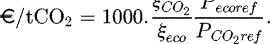
Value of an avoided yearly hour of power cut:
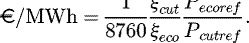
The values of the weighting coefficients ξ proposed here correspond to giving a value of 47 € to the avoided ton of CO2, and of 0.79 €/MWh to the avoided yearly hour of power cut. Other values for the weighting coefficients can be used by interested readers if they wish to use the open access MIXOPTIM software to perform their own calculations.
By definition, this global figure of merit is dimensionless and equal to unity for the reference mix (here, the mix EU 2013). It is interesting to see how this figure of merit varies for small variations of the composition of the mix by calculating the sensitivity to changes in the installed power αi of the source i:

Here, the partial derivatives 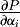 have been approximated as
have been approximated as 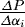 with Δαi = 20 GW.
with Δαi = 20 GW.
Table 6 below gives the sensitivity of the global figure of merit to a change in the installed power αi of the source i.
A lower criterion value corresponds to an improvement of the mix performance. Consequently, if an increase of the installed power αi of the source i results in a negative value of the sensitivity 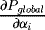 , this increase corresponds to an improvement of the mix performance, according to the global criterion. Table 6 shows that the largest improvement of the global figure of merit of the mix is obtained via an increase of the installed nuclear power.
, this increase corresponds to an improvement of the mix performance, according to the global criterion. Table 6 shows that the largest improvement of the global figure of merit of the mix is obtained via an increase of the installed nuclear power.
This study uses the OECD 2010 cost structure, established before the Fukushima accident [3]. The additional safety requirements imposed on the nuclear reactors after the accident may modify the fixed costs of the Gen II and Gen III nuclear power. This effect has not been taken into account here. On the other hand, the fixed cost of solar, and, to a lesser extent, wind power, is steadily decreasing, and the 2010 figures are already slightly outdated. More recently, the cost of gas has also decreased, especially in the United States, where some Gen II reactors have been recently closed because they were no longer economically competitive. The above figures are therefore probably somewhat too pessimistic for renewable sources, and too optimistic for nuclear Gen II and III.
Another approximation made in this study must also be mentioned: Europe has been treated as a “copperplate”, assuming no restriction to the power transfer from one region to the other. This global treatment results in an underestimate of the use of expensive but locally available sources that are needed more often in reality than in the simulation because of regional interconnexion limitations.
The performance of the 2013 EU power mix, calculated by MIXOPTIM as a reference basis.
The sensitivity of the EU power mix to changes in the installed power for the various power sources. The quantities Delta cost, Delta CO2 and Delta Pcut are the changes in cost, CO2 production and power cut probability induced by a 20 GW increase in installed power for a given power source, wind, solar, hydraulic, etc.
The sensitivity of the global figure of merit of the EU power mix to an elementary change in installed power.
6 Conclusions
With the above reservations in mind, the study shows that a possible way to keep an affordable MWh in Europe with minimal amount of CO2 production and acceptable security of supply could be to extend the life of existing Gen II nuclear reactors, provided this extension can be made in reasonable safety conditions. All other options lead to the degradation of the mix performance, on at least one of the three criteria listed above. An increase of the Gen III installed nuclear power degrades slightly the economic performance of the mix, but improves its global performance.
Acknowledgments
This work has been conducted under the auspices of the National Agency for the Coordination of Research on Energy (ANCRE), with the financial support of the NEEDS Program.
References
- B. Bonin et al., MIXOPTIM: a tool for the evaluation and the optimization of the electricity mix in a territory, Eur. Phys. J. Plus 129, 198 (2014) [CrossRef] [EDP Sciences] [Google Scholar]
- F. Wagner, Electricity by intermittent sources: an analysis based on the German situation 2012, Eur. Phys. J. Plus 129 20 (2014) [CrossRef] [EDP Sciences] [Google Scholar]
- Projected costs of generating electricity, report OECD/NEA, 2010 [Google Scholar]
- H. Safa, CO2 production, Rev. Gen. Nucl. 2 100 (2012) [Google Scholar]
- RTE website: http://www.rte-france.com/fr/eco2mix/eco2mix [Google Scholar]
- F. Thais et al., Energy Handbook, edited by CEA (Institut de Technico-économie des Systèmes Énergétiques, 2013), www.cea.fr [Google Scholar]
Cite this article as: Bernard Bonin, Henri Safa, Françoise Thais, Axel Laureau, Elsa Merle-Lucotte, Joachim Miss, Danylo Matselyuk, Yann Richet, François-Marie Bréon, The role of power sources in the European electricity mix, EPJ Nuclear Sci. Technol. 3, 10 (2017)
All Tables
Comparison between the observed and calculated load factors of the sources for the 2013 EU power mix.
The performance of the 2013 EU power mix, calculated by MIXOPTIM as a reference basis.
The sensitivity of the EU power mix to changes in the installed power for the various power sources. The quantities Delta cost, Delta CO2 and Delta Pcut are the changes in cost, CO2 production and power cut probability induced by a 20 GW increase in installed power for a given power source, wind, solar, hydraulic, etc.
The sensitivity of the global figure of merit of the EU power mix to an elementary change in installed power.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


