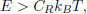EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 9 (2023) EPJ Nuclear Sci. Technol., 9 (2023) 23 Full HTML
Open Access
Issue
EPJ Nuclear Sci. Technol.
Volume 9, 2023
Article Number 23
Number of page(s) 11
DOI https://doi.org/10.1051/epjn/2023006
Published online 31 May 2023

© H. Belanger et al., Published by EDP Sciences, 2023

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

Currently, two internationally accepted nuclear data storage formats are in use. The traditional and most widely used is the ENDF-6 format [1]. All major data libraries are distributed in this format, and its use is ubiquitous in nuclear engineering, nuclear physics, and reactor physics communities [2–4]. The ENDF-6 format does not store nuclear data in a representation which is conducive to use in a continuous-energy Monte Carlo transport code. Secondary energy and angle distributions are often stored in representations which cannot be easily sampled to obtain the outgoing energy and scattering angle after a collision. Important data such as the Cumulative Distribution Function (CDF) are not provided, and the provided tabulations for a Probability Density Function (PDF) may not be linearly interpolable. The cross sections for reactions in the ENDF files distributed with major data libraries are generally kept as resonance parameters, and not as a linearly interpolable set of points [1]. Due to these reasons, ENDF-6 formatted files are generally not read directly for nuclear data in Monte Carlo transport codes.

A new format for nuclear data files has recently been developed, called the Generalised Nuclear Data Structure (GNDS) [5]. The GNDS format makes many improvements on the ENDF-6 format, such as allowing the storage of energy and angle distributions in a format which is more compatible with continuous-energy Monte Carlo codes (although this is not required by the standard). Some nuclear data libraries are now also distributed in the GNDS format (such as ENDF/B-VIII.0 and TENDL-2021) [3, 6], but these distributions are generally translations of the ENDF-6 formatted files, and therefore do not contain data which is Monte Carlo ready. As GNDS is so young, there is currently very little support for the format in most software. While the FUDGE nuclear data processing code does have support for GNDS [7, 8], other major codes such as NJOY and FRENDY do not yet support the format [9, 10].

Because not all necessary data for continuous-energy Monte Carlo transport codes is provided in ENDF-6 files (and in practice, is not

available in the current GDNS files either), most Monte Carlo codes use an alternative format which contains cross sections that are linearly interpolable and represent PDFs and CDFs

in a format that lends itself well to Monte Carlo sampling (typically piecewise linear functions). The Monte Carlo code MCNP developed its own file format for this purpose, which is referred to

as ACE (ACE being an acronym for A Compact ENDF) [11]. The official format for ACE files is essentially the MCNP implementation, as ACE files were generally only intended for use with MCNP. A description of this format is provided in the development manual of MCNP, but this is typically not available to users. Despite the lack of publicly available documentation, the ACE format has become an extremely popular choice for many Monte Carlo codes. Codes which use ACE files include Serpent [12], the open-source Monte Carlo SCONE [13], and a plethora of others [14–16].

The popularity of the ACE format has likely been driven by the ubiquitous use of MCNP, which has ensured that most users have several ACE libraries at hand already. Since MCNP is used so frequently in the field, it has also become popular for other Monte Carlo codes to compare their results to those obtained using MCNP. Such a code-to-code comparison can be simplified if both codes are using the same nuclear data files, as any statistically significant differences in results would therefore be due to different approximations made in the physics at hand. As the use of the ACE format has expanded, it has become a “de facto” standard in the community, and a publicly accessible document has now been produced outlining the format [17]. Currently, two open-source nuclear data processing codes are available to produce ACE files from ENDF-6 evaluations. NJOY is the more traditional choice and can produce ACE files for incident neutrons, photons, thermal scattering laws, and several different charged particles [9, 18]1. A newer option is the FRENDY processing code, which can produce ACE files for incident neutrons and thermal scattering laws [10].

This paper presents version 0.3.1 of the Papillon Nuclear Data Library (PapillonNDL) [19]. PapillonNDL is a free and open-source library which allows users to read and sample ACE files for incident neutron data, and thermal scattering laws. Being written in C++, PapillonNDL can be used to write high-performance computing applications. Additionally, a Python API is provided, which grants users access to all of the same functionality as in the C++ API.

Continuous-energy nuclear data is invaluable in the field of nuclear engineering and is used for nuclear reactor calculations, radiation protection, and nuclear medicine. Due to their importance, many aspects of nuclear data are discussed and taught in nuclear engineering programs, at the undergraduate and graduate levels. Most of these discussions are focused on continuous-energy cross-sections, but may also include secondary energy and angle distributions as well. Most classroom usage of nuclear data (if any) is generally quite minimal and surface-level. A large reason for this is limited access to continuous-energy data. The Python interface of PapillonNDL gives students a way to read ACE files in an easy and accessible programming language, so that they can easily examine, plot, and use continuous-energy neutron data.

Three alternatives exist to reading ACE files in Python: PyNE [20], OpenMC [21], and ACEtk [22]. While it is possible to make plots of cross-sections and scattering distributions with these three implementations, none of them supports the sampling of secondary energy or angle distributions. It is therefore impractical to use these libraries when a user needs to sample scattering energies and angles, as the user would need to implement all of the sampling algorithms themselves. Outside of the Python language, JANIS is a popular tool for plotting different pieces of nuclear data (written in Java), but it is not designed to be used as a library in other applications, cannot read ACE files, and cannot sample scattering distributions [23]. While it is also possible to plot data in ACE files using NJOY, users have very little control over the final appearance of such plots [9]. PapillonNDL provides a simple interface to users, making it easy to sample scattering distributions (even elastic scattering) and plot nuclear data. To the best of the author’s knowledge, it is the only such stand-alone library which exists, for both C++ and Python.

Most graduate students who study computational methods in nuclear engineering will be required at one point in time to write a small toy Monte Carlo code. Typically, these exercises are left to simple one-group problems (or at most, a few groups), with isotropic scattering. Being able to easily sample scattering distributions with PapillonNDL using the Python API, students can easily write toy Monte Carlo codes in continuous energy. A continuous-energy code written in pure Python, however, would be most probably too slow for high-performance computing applications. PapillonNDL’s Python API being made available via pybind11 means all computations are actually performed in compiled and optimized C++, allowing for reasonable computation times. Graduate students are not the only ones however who find themselves writing small toy Monte Carlo codes; senior researchers often write “disposable” Monte Carlo codes, as this is where the development of new algorithms and ideas typically takes place. PapillonNDL fills this niche as well, providing an easy interface for researchers to write simple, disposable, continuous-energy Monte Carlo codes, to test new computational methods in C++.

The remainder of this paper is structured as follows: Section 2 describes the overall functionality of the library, providing brief explanations of the main features and classes. The process which has been used to verify the correct function of the library is presented in Section 3, in addition to an example Monte Carlo benchmark result. Details on the development and distribution of the library are provided in Section 4. Conclusions and future development goals are outlined in Section 5.

2. Library structure and neutron physics

PapillonNDL is written in C++ and makes heavy use of the object-oriented programming paradigm. Currently, all continuous-energy neutron physics is supported by the library. It is possible to read continuous-energy ACE files for free-gas data, and make use of reaction cross sections, scattering distributions, information about delayed neutron families, and probability tables for the unresolved resonance region. Additionally, it is also possible to read the ACE files which contains thermal scattering laws, and sample the three types of bound thermal scattering laws which are generally considered in neutron physics. In this section, we will cover the major functionalities of the library and the important classes and interfaces which users will likely need to interact with.

Free-gas continuous-energy neutron data is accessed through the STNeutron class (ST standing for Single Temperature). A STNeutron instance contains all cross-sections, scattering distributions, fission data, and probability tables for a single nuclide, at a single temperature. Many users have ACE libraries which were distributed with MCNP or Serpent. PapillonNDL has two helper classes, MCNPLibrary and SerpentLibrary, which can read each code’s respective cross-section directory file. A user can then ask the library to load the STNeutron instance for a particular nuclide and temperature. Alternatively, a STNeutron instance can be created directly from an ACE file. While the library assumes ASCII ACE files by default, one can also use binary ACE files. The ACE class in PapillonNDL even provides a utility to convert an ASCII ACE file to a binary ACE file for the system in question2.

The total, elastic, and fission cross sections are stored as CrossSection instances, directly in the STNeutron object. Reaction-specific cross sections are stored in the respective STReaction object, which also contains other pieces of reaction specific information, such as the scattering yield as a function of incident energy and the scattering distribution. In the ACE format, all cross-sections associated with a given nuclide/temperature combination are stored on the same energy grid. In many classes of neutron transport problems, the most time-consuming portion of the Monte Carlo algorithm is the search for the index of the energy grid that contains the energy of the neutron [24]. To mitigate this problem, PapillonNDL employs the energy-hashing algorithm on each nuclide/temperature combination, as proposed by Brown [25]. Previous studies have looked at different energy-grid search strategies, and identified energy-hashing as likely being the best compromise between speed and memory usage [24].

For many resonant nuclides, it is impossible to know the exact resonance parameters above a certain energy threshold, as the resonances are too close to one another. This region is referred to as the Unresolved Resonance Region (URR), and in this energy window, the cross-section values are only known statistically. In the ACE format, the URR cross sections are represented using the probability table method [9, 26]. PapillonNDL will read the URR probability tables, storing them in a URRPTables instance, which is kept in the STNeutron object. A user may sample cross-sections with the incident energy and a single random number on the unit interval. The URRPTables instance will then return an XSPacket, containing the total, elastic, inelastic, absorption, fission, and capture cross-sections, in addition to the heating number3. The provided random numbers may be stored by the user, and reused to ensure that correlations are maintained when evaluating cross sections in the URR for the same nuclide, but at different temperatures.

2.1. Scattering distributions

All scattering and absorption reactions (other than elastic scattering and fission) are stored in the STNeutron object and can be accessed via their respective MT number4. The scattering distribution for each reaction, which is used to sample the outgoing neutron’s energy and the cosine of the scattering angle, is stored in the reaction’s STReaction instance. Scattering distributions are accessed through the interface of the abstract AngleEnergy class. To sample an outgoing energy and scattering angle cosine, the incident energy must be provided, in addition to a function which generates pseudo-random double precision floating point numbers, uniformly distributed on the unit interval. With this interface, a user is free to supply whatever pseudo-random number generator they desire, without needing to recompile the library. It is up to the user to ensure that their provided random number function will only generate values within [0, 1). No checks are performed on the sampled random numbers to ensure that they are within this interval. If the random number function provides a value outside this interval, the behaviour of the library is not guaranteed and is undefined. A random number generator function is provided in the library and should be suitable for most users’ basic needs should they not wish to provide their own.

The ACE format contains many different possible representations of scattering distributions [17]. Currently, the following scattering distributions are supported:

  • uncorrelated.

  • Kalbach-Mann.

  • Tabular Energy-Angle.

  • N-Body Phase Space Distribution.

For uncorrelated distributions, the angular distribution is sampled independently from the energy distribution. Some of the energy distributions described in the ACE specification are legacy or do not appear in any modern evaluations, and have not been implemented. The correlated Laboratory Angle-Energy distribution is not implemented either, as it does not appear in any modern evaluation. In both the ENDF and ACE formats, reactions may store their scattering distributions in the centre-of-mass frame [1, 17]. When this is the case, the distribution is encapsulated inside a special CMDistribution distribution, which automatically converts the resulting scattering information from the centre-of-mass frame to the laboratory frame. The users, therefore, do not need to worry about performing this conversion themselves. Reactions which do not emit any neutrons are given a special scattering distribution, Absorption, which throws an exception when one tries to sample an energy-angle pair. Other types of secondary particles (such as photons) are not yet supported, but this feature is planned for the future when photon physics is supported.

2.2. Elastic scattering

Elastic scattering is not treated in the same manner as other scattering reactions, which are stored in STReaction instances. Instead, a special class, Elastic, is stored in the STNeutron instance. Elastic inherits from AngleEnergy, and it is, therefore, possible to sample scattering information from an Elastic instance in the same manner as for the distributions of other reactions. The reason that elastic scattering is treated differently is that one must consider the thermal motion of the target nucleus when performing the kinematics calculations to sample elastic scattering. This treatment to consider the temperature effect on the scattering distribution is often referred to as Doppler broadening5. Several algorithms exist to perform the Doppler broadening of the elastic scattering kernel. Most Monte Carlo codes use the Sampling Velocity of the Target nucleus (SVT) algorithm [28, 29], also sometimes referred to as the constant cross-section (CXS) approximation [30]. This algorithm relies on an approximation which is only valid when the elastic scattering cross-sections are nearly constant with respect to the incident energy. Rothenstein, however, has demonstrated that the use of this algorithm on nuclides which have resonances at low energies (such as 238U) yields incorrect results and proposed an exact treatment referred to as the Doppler-broadening Rejection Correction (DBRC) [31]. Subsequently, Becker et al. demonstrated that the application of DBRC can have a significant impact on the multiplication factor for criticality problems, leading to differences as high as 360 pcm when compared to SVT [32].

thumbnail Fig. 1.

Example Jupyter notebook using PapillonNDL’s Python API to compare elastic scattering for a 36.25 eV neutron sampled using both SVT and DBRC off of 238U.

Due to the large effect that elastic scattering can have on simulation results, PapillonNDL treats elastic scattering separately from other reactions, so as to give users fine-grained control of the algorithm being used by the Elastic class. On a nuclide-by-nuclide basis, one can decide whether or not to use the target at rest (TAR) approximation. The TAR approximation will be applied for neutrons with incident energy

(1)

kB being the Boltzmann constant, and T being the temperature of the material (in kelvin). CR is a positive parameter which can be set by the user and can vary for each nuclide. By default, PapillonNDL will allow the TAR approximation to be used for all nuclides, with CR = 400. Users can also specify the use of either SVT or DBRC for elastic scattering, by providing the appropriate ElasticDopplerBroadener, which is responsible for sampling the velocity of the target nucleus. The ElasticSVT is used by default, as it requires no extra information beyond that provided in ACE files for a given nuclide/temperature combination. The DBRC algorithm requires the elastic scattering cross section for the nuclide at 0 K. If users have this cross section (either from another ACE file, or elsewhere), it may be used to construct an ElasticDBRC instance, which can be provided to the Elastic instance of the nuclide. A Python example is provided in Figure 1, demonstrating the use of both SVT and DBRC for 238U, and the resulting differences in the scattering kernel near a low-energy resonance.

2.3. Fission data

Fission, like elastic scattering, is somewhat unique and is treated differently from other reactions in PapillonNDL. A Fission class provides access to the prompt neutron spectrum, in addition to the prompt, total, and delayed neutron yields per fission, all given as functions of the incident energy. The information such as the decay constant, probability, and emission energy spectrum are provided for each delayed family in a DelayedFamily class. Most evaluations provide the average prompt fission spectrum directly, using MT 18. Occasionally, however, evaluators will instead choose to provide the data for first-chance, second-chance, third-chance, and fourth-chance fission directly, in MT 19, 20, 21, and 38 respectively. When this is the case, the total prompt spectrum is reconstructed from these four reactions. Nuclides which are not fissile still have a Fission class instance: there are simply no delayed families and the fission yields are all set to zero.

2.4. Thermal scattering laws

Only free-gas neutron data is stored in the STNeutron class. To interact with thermal scattering laws which contain the information for coherent elastic, incoherent elastic, and incoherent inelastic scattering, the STThermalScatteringLaw class is used. PapillonNDL supports both the traditional discrete energies and cosines representation for incoherent inelastic scattering and the newer representation with continuous energies and discrete cosines [9]. Each type of thermal neutron scattering channel is represented by an instance of the abstract STTSLReaction class, which can be sampled in the same manner as a scattering distribution, but can also be queried for the cross-section value. While all thermal scattering evaluations must contain incoherent inelastic scattering, coherent and incoherent elastic may or may not be present [1]. As such, PapillonNDL has been written in such a way so that a user can still query the cross section and scattering information for these reactions (even if they are not present), without causing any errors or segmentation faults. The cross section in this case is simply guaranteed to be zero, while the scattering distribution will throw an exception when sampled (like the Absorption distribution).

3. Library verification

To verify that PapillonNDL correctly samples scattering distributions, from both free-gas and thermal scattering laws, the library was tested on Lib80x and ENDF80SaB2, the official ACE libraries prepared by Los Alamos National Laboratory from ENDF/B-VIII.0 for use with MCNP [33]. When reading an ACE file, and constructing a STNeutron instance, PapillonNDL performs many tests on the data, to ensure that the cross-sections and scattering distributions are coherent. These tests include: ensuring all cross-sections and PDFs are positive; CDFs must be in increasing order, starting at 0 and ending at 1; other common-sense checks such as angle cosines being in the [ − 1, 1] interval. PapillonNDL is able to read all of the free-gas ACE files distributed with Lib80x, except those for 22Na (at all temperatures), 115mCd (at all temperatures), and 111Cd (at 0.1 K). For these ACE files, PapillonNDL will throw an exception, due to failures of the aforementioned checks. The reason for these failures is as follows:

  • a negative capture cross-section is present in the URR probability tables for 111Cd at 0.1 K.

  • An outgoing energy grid for the MT 91 scattering distribution for 115mCd is not sorted.

  • Several of the URR probability tables for 22Na have a CDF of 0 (while CDFs for scattering distributions should start at 0, this is not the case for URR probability tables).

The problems with 111Cd and 115mCd were previously unreported. The Lib80x report mentions that negative cross-sections had been found in the URR probability tables for 22Na, but that the data had been reprocessed without using URR probability tables [33, 34]. However, the 22Na ACE files appears to still contain the URR probability tables. In addition to these unexpected errors, many negative heating numbers were encountered in several evaluations, but all had been previously mentioned in the Lib80x release, and are caused by problems in the original ENDF evaluations. To allow these evaluations to be used by the user, the check for positive cross-sections is not performed if it is indicated that the CrossSection object is being used to contain heating numbers.

thumbnail Fig. 2.

Comparison of PapillonNDL and OpenMC for an Uncorrelated scattering distribution, using a Maxwellian spectrum for energy. The demonstrated distribution is for 241Pu MT18, at an incident energy of eV. The p-values for the energy and angle distributions are 0.496 and 0.548 respectively.
thumbnail Fig. 3.

Comparison of PapillonNDL and OpenMC for a Kalbach-Mann scattering distribution. The demonstrated distribution is for 16O MT28, at an incident energy of 20 MeV. The p-values for the energy and angle distributions are 0.962 and 0.159 respectively.

Many negative values for scattering PDFs were initially encountered in the distributions for incoherent inelastic scattering. As the magnitude of these negative values was quite small (typically around 10−20), it was determined that such small negative values could simply be set to zero. A threshold is used, where any negative PDF value that is in the interval ( − 10−15, 0] is set to zero; all negative values for scattering PDFs in the interval ( − ∞, −10−15] result in an exception being thrown. Another error which was initially encountered was that the discrete scattering cosines in the incoherent inelastic distributions were often not sorted. This can be problematic when applying the “smearing” operation to smooth out the scattering angles so that they appear to be a continuous distribution. Since these discrete angles are all equiprobable, it was decided that simply sorting these angles is an appropriate solution. With these adjustments, PapillonNDL is able to read all ACE files for thermal scattering laws which are distributed with ENDF80SaB2. Attempting to read older libraries, such as ENDF71SaB can lead to errors, however, as some of the provided discrete cosines are outside the [ − 1, 1] interval. The only solution to this problem is to generate new ACE files for these evaluations, as this problem has been fixed in more recent versions of NJOY2016 [35].

3.1. Comparison with OpenMC

There is a small set of unit tests which are run automatically during the development of the library, which makes sure that underlying library functionality is properly functioning. These tests ensure that performing table interpolations and sampling angular distributions are done properly, and yield the expected results. Ensuring the proper implementation of joint angle-energy distributions is more difficult, however. Currently, instead of using unit tests, two supplementary programs are provided with PapillonNDL, allowing the user to directly sample a specified scattering distribution at a specified energy, using either PapillonNDL or OpenMC. Both programs write all of the sampled energy and cosine pairs to a binary NumPy file. These files are then read by a provided Python script which then performs a Kolmogorov–Smirnov test on the two data sets, verifying that PapillonNDL yields statistically equivalent results to OpenMC. After performing its analysis on the two data sets, the Kolmogorov–Smirnov test will return a p-value, which indicates the probability that the two data sets were sampled from the same probability distribution. In general, it is considered that if the p-value for both energy and the cosine of the scattering angle is greater than 0.05, then the distributions are statistically equivalent. The one exception to this is the distribution of coherent elastic scattering. The angular distribution for this reaction is a discrete distribution, given as a function of the energies of the Bragg edges for the material. PapillonNDL stores all energy quantities in units of MeV, while OpenMC uses units of eV. This units conversion slightly changes the floating-point representation of the Bragg edges, and therefore also slightly affects the discrete distribution for the scattering angle. This slight difference in a discrete distribution will often cause the Kolmogorov–Smirnov test to fail, despite the distributions being equivalent. For this case, it is just ensured that the two distributions appear to be equivalent upon a visual examination of the two plotted distributions.

thumbnail Fig. 4.

Comparison of PapillonNDL and OpenMC for a Tabular Energy-Angle scattering distribution. The demonstrated distribution is for 235U MT16, at an incident energy of 10 MeV. The p-values for the energy and angle distributions are 0.446 and 0.513 respectively.
thumbnail Fig. 5.

Comparison of PapillonNDL and OpenMC for an NBody scattering distribution. The demonstrated distribution is for 2H MT16, at an incident energy of 10 MeV. The p-values for the energy and angle distributions are 0.373 and 0.341 respectively.

When testing PapillonNDL, different nuclides and reactions were independently examined. For a given nuclide/reaction combination, several incident energies were calculated, based on the threshold energy of the reaction, and the maximum tabulated energy for the nuclide. Each nuclide/reaction/incident energy combination was used to sample a set of outgoing energy and cosine pairs from PapillonNDL and OpenMC. These datasets were then compared to ensure they were statistically equivalent. It is impossible to present the results of all the tests here, but a few different examples of such comparisons are provided in this paper. Figures 2–5 depict the comparisons for examples of Uncorrelated, Kalbach-Mann, Tabular Energy-Angle, and NBody distributions respectively. In general, an excellent agreement has been observed between PapillonNDL and OpenMC.

The elastic scattering implementation in the two codes is quite different. OpenMC will perform the kinematics calculations directly on the particle in transport, changing the energy and direction directly. A cosine of the scattering angle is not actually sampled (at least not in the laboratory frame). PapillonNDL is agnostic to such concepts and is meant to be used in any general Monte Carlo code, or as a stand-alone distribution sampler. For elastic scattering, PapillonNDL will perform a similar kinematics calculation, but on a “pseudo-particle” which is created internally, always with the same initial direction. After the kinematics calculation has been performed, the outgoing energy and scattering angle in the laboratory frame are all that is returned. A comparison of the two DBRC implementations for elastic scattering is presented in Figure 6. An example comparison of PapillonNDL and OpenMC for incoherent inelastic scattering off of 1H in light water is presented in Figure 7. In general, excellent agreement was observed between both codes across the range of examined energies.

thumbnail Fig. 6.

Comparison of PapillonNDL and OpenMC implementation of elastic scattering with DBRC. The demonstrated distribution is for 238U at 293.6 K and incident energy of 36.26 eV. The p-values for the energy and angle distributions are 0.666 and 0.927 respectively.
thumbnail Fig. 7.

Comparison of PapillonNDL and OpenMC for an incoherent inelastic scattering with 1H in water at 293.6 K, and at an incident energy of 0.99 eV. The p-values for the energy and angle distributions are 0.806 and 0.875 respectively.
thumbnail Fig. 8.

Flux profile for the CROCUS research reactor at EPFL, simulated using the Chenille Monte Carlo mini-app, with PapillonNDL for continuous-energy neutron physics.

3.2. Integral test on a continuous-energy Monte Carlo benchmark

Previously, PapillonNDL has been used to add full continuous-energy neutron physics to the MGMC multi-group Monte Carlo mini-app [36]. The resulting continuous energy Monte Carlo mini-app, named Chenille, is able to perform fixed-source, k-eigenvalue, and neutron noise calculations in continuous-energy, and general three-dimensional geometries [37]. Several different continuous-energy benchmarks have been examined using Chenille. As a form of integral test for the Papillon Nuclear Data Library, the ‘H1 water-level’ configuration of the CROCUS reactor benchmark has been examined [38]. Using ACE files produced from the ENDF/B-VII.0 evaluation [39], processed using version 2 of FRENDY [10], a multiplication factor of keff = 1.00249 ± 0.00002 was obtained. Other studies have previously obtained multiplication factors of keff = 1.00249 ± 0.000024 using TRIPOLI-4®, and keff = 1.00253 ± 0.000012 using MCNP5 using the same data library [40]. Despite not having used probability tables to treat the unresolved resonance region (a fine approximation for a thermal system such as CROCUS), the agreement between Chenille and these two previous values is excellent. Figure 8 provides plots of the flux profile for the benchmark obtained with Chenille.

4. Development and distribution

PapillonNDL is written in C++, using the recent C++20 standard. Features such as std::span, std::ranges, and std::source_location provide a rich set of features and abstractions which facilitate development. Modules were also introduced in C++20, but the library does not currently make use of this feature, due to the lack of uniform compiler support. The choice of C++20 helps ensure the longevity of the project, as compiler support for this standard will only increase with time. Currently, however, it means that the choice of available compilers is rather limited. On GNU/Linux and BSD systems, PapillonNDL has been successfully compiled with GCC 11, GCC 12, and Clang 15 when using libstdc++ (libc++ does not yet support all required C++20 features). It is also possible to build PapillonNDL on Windows systems using MSVC version 19.29 or higher. In addition to a sufficient C++20 compiler, CMake is also required, as it is the build system used for the project. No other dependencies are required to build PapillonNDL if one only intends to use the C++ API.

The Python API is generated using the pybind11 library. This dependency is automatically downloaded by CMake if the Python bindings option is enabled. Additionally, Python must also be installed on the system, with the required development header files. Each class in the library has bindings which make it possible to use the exact same C++ interface from within Python, resulting in one uniform API for the two languages. Documentation is generated from the C++ source using Doxygen, and currently also serves as the documentation for the Python API.

PapillonNDL is currently developed publicly on GitHub, at https://github.com/HunterBelanger/papillon-ndl, and is released under the GPL-3.0-or-later license. The documentation website, with the full API description and usage examples in both Python and C++ can be found at https://papillon-ndl.readthedocs.io.

5. Conclusions and future developments

The Papillon Nuclear Data Library (PapillonNDL) is a stand-alone C++ and Python library, which can be used to read and interact with continuous-energy nuclear data stored in ACE files. Currently, both free-gas data for neutrons, and thermal scattering law ACE files can be read by the library, giving users access to all continuous-energy neutron physics. It has been written with the express goal of facilitating fundamental research and nuclear engineering education. Experienced researchers will find utility in the library, as the C++ interface makes it easy to implement small continuous-energy Monte Carlo codes to test new simulation methods and algorithms, as part of the research process. The Python interface makes it easy for students to gain access to continuous-energy nuclear data. PapillonNDL is distributed as free and open-source software, and can be used on all major operating systems, making it a valuable tool in the classroom. The implementation of the sampling routines in the library has been tested by sampling sets of scattering energy-angle pairs from both PapillonNDL and OpenMC. Kolmogorov–Smirnov tests were used to check that the two sampled sets were statistically equivalent. This verification was performed using Lib80x, and for all distributions which have been examined, an excellent statistical agreement has been observed.

In the future, it is hoped that the development of the library will continue. Short-term goals are focused on improving the representation of thermal scattering laws. Both incoherent elastic and incoherent inelastic scattering use discrete distributions for scattering angles [9]. By using the Debye-Waller integral which is provided in the ENDF files for thermal scattering laws, it is possible to use a continuous distribution for the scattering angle in incoherent elastic scattering [1]. It is also possible to use the S(α, β) tables provided in ENDF files to generate a representation for incoherent inelastic scattering which is continuous in both energy and angle [41, 42]. An interface to perform Doppler broadening of cross sections is currently in development, and will hopefully be integrated in the near future. In the long term, it is hoped that physics for other particles will be added to the library, so that it can handle photo-atomic, photo-nuclear, dosimetry, and electron ACE files.

Conflict of interests

The author declares that they have no competing interests to report.

Acknowledgments

The author would like to thank Dr. Davide Mancusi and Dr. Andrea Zoia, at CEA Paris-Saclay Service d’Études des Réacteurs et de Mathématiques Appliquées, for their invaluable discussions and helpful comments in the preparation of this manuscript.

Funding

This research did not receive any specific funding.

Data availability statement

All data used in this article is readily reproducible from the presented open-source software library and the cited nuclear data libraries.

Author contribution statement

Hunter Belanger: conceptualization, software, investigation, validation, writing – original draft, writing – review & editing.

1

NJOY is the only official processing code for producing ACE files to be used with MCNP.

2

Binary ACE files are not generally usable on all other computers, as different systems can use a different “endianness”.

3

Heating numbers are used to simulate the amount of heating deposition and damage to materials.

4

MT numbers are uniquely associated with different reactions, according to the ENDF-6 format [1].

5

Doppler broadening also refers to the treatment of cross-sections for use at different temperatures, taking into account the thermal motion of the atoms in the material, assuming they have the same velocity distribution as an ideal free-gas [27].

References

  1. Members of the Cross Sections Evaluation Working Group, ENDF-6 Formats Manual, Brookhaven National Laboratory, Tech. Rep. BNL-203218-2018-INRE, 2018 [Google Scholar]
  2. A.J.M. Plompen, O. Cabellos, C.D.S. Jean, M. Fleming, A. Algora, M. Angelone, P. Archier, E. Bauge, O. Bersillon, A. Blokhin, F. Cantargi, A. Chebboubi, C. Diez, H. Duarte, E. Dupont, J. Dyrda, B. Erasmus, L. Fiorito, U. Fischer, D. Flammini, D. Foligno, M.R. Gilbert, J.R. Granada, W. Haeck, F.-J. Hambsch, P. Helgesson, S. Hilaire, I. Hill, M. Hursin, R. Ichou, R. Jacqmin, B. Jansky, C. Jouanne, M.A. Kellett, D.H. Kim, H.I. Kim, I. Kodeli, A.J. Koning, A.Y. Konobeyev, S. Kopecky, B. Kos, A. Krása, L.C. Leal, N. Leclaire, P. Leconte, Y.O. Lee, H. Leeb, O. Litaize, M. Majerle, J.I.M. Damián, F. Michel-Sendis, R.W. Mills, B. Morillon, G. Noguére, M. Pecchia, S. Pelloni, P. Pereslavtsev, R.J. Perry, D. Rochman, A. Röhrmoser, P. Romain, P. Romojaro, D. Roubtsov, P. Sauvan, P. Schillebeeckx, K.H. Schmidt, O. Serot, S. Simakov, I. Sirakov, H. Sjöstrand, A. Stankovskiy, J.C. Sublet, P. Tamagno, A. Trkov, S.V.D. Marck, F. Álvarez Velarde, R. Villari, T.C. Ware, K. Yokoyama, G. Žerovnik, The joint evaluated fission and fusion nuclear data library, JEFF-3.3, Eur. Phys. J. A 56, 181 (2020) [CrossRef] [Google Scholar]
  3. D. Brown, M. Chadwick, R. Capote, A. Kahler, A. Trkov, M. Herman, A. Sonzogni, Y. Danon, A. Carlson, M. Dunn, D. Smith, G. Hale, G. Arbanas, R. Arcilla, C. Bates, B. Beck, B. Becker, F. Brown, R. Casperson, J. Conlin, D. Cullen, M.-A. Descalle, R. Firestone, T. Gaines, K. Guber, A. Hawari, J. Holmes, T. Johnson, T. Kawano, B. Kiedrowski, A. Koning, S. Kopecky, L. Leal, J. Lestone, C. Lubitz, J.M. Damián, C. Mattoon, E. McCutchan, S. Mughabghab, P. Navratil, D. Neudecker, G. Nobre, G. Noguere, M. Paris, M. Pigni, A. Plompen, B. Pritychenko, V. Pronyaev, D. Roubtsov, D. Rochman, P. Romano, P. Schillebeeckx, S. Simakov, M. Sin, I. Sirakov, B. Sleaford, V. Sobes, E. Soukhovitskii, I. Stetcu, P. Talou, I. Thompson, S.V.D. Marck, L. Welser-Sherrill, D. Wiarda, M. White, J. Wormald, R. Wright, M. Zerkle, G. Žerovnik, Y. Zhu, ENDF/B-VIII.0: the 8th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data, Nucl. Data Sheets 148, 1 (2018) [CrossRef] [Google Scholar]
  4. K. Shibata, O. Iwamoto, T. Nakagawa, N. Iwamoto, A. Ichihara, S. Kunieda, S. Chi, K. Furutaka, N. Otuka, T. Ohasawa, T. Murata, H. Matsunobu, A. Zukeran, S. Kamada, J.-I. Katakura, JENDL-4.0: a new library for nuclear science and engineering, J. Nucl. Sci. Technol. 48, 1 (2011) [CrossRef] [Google Scholar]
  5. NEA, Specifications for the Generalised Nuclear Database Structure (GNDS), Nuclear Energy Agency, Tech. Rep. [Online], 2020, Available: https://www.oecd-nea.org/jcms/pl_39689/specifications-for-the-generalised-nuclear-database-structure-gnds?details=true [Google Scholar]
  6. A. Koning, D. Rochman, J.-C. Sublet, N. Dzysiuk, M. Fleming, S. van der Marck, TENDL: complete nuclear data library for innovative nuclear science and technology, Nucl. Data Sheets 155, 1 (2019), Special Issue on Nuclear Reaction Data. [Online], Available: https://www.sciencedirect.com/science/article/pii/S009037521930002X [CrossRef] [Google Scholar]
  7. C. Mattoon, B. Beck, N. Patel, N. Summers, G. Hedstrom, D. Brown, Generalized nuclear data: a new structure (with supporting infrastructure) for handling nuclear data, Nucl. Data Sheets 113, 3145 (2012) [CrossRef] [Google Scholar]
  8. FDUGE. [Online], Available: https://github.com/LLNL/fudge [Google Scholar]
  9. R. Macfarlane, D.W. Muir, R.M. Boicourt, A.C. Kahler, J.L. Conlin, The NJOY nuclear data processing system, version 2016, Los Alamos National Laboratory, Tech. Rep. LA-UR-17-20093, 2017 [CrossRef] [Google Scholar]
  10. K. Tada, Y. Nagaya, S. Kunieda, K. Suyama, T. Fukahori, Development and verification of a new nuclear data processing system FRENDY, J. Nucl. Sci. Technol. 54, 1 (2017) [Google Scholar]
  11. X-5 Monte Carlo Team, MCNP-A general Monte Carlo N-particle transport code, version 5, Los Alamos National Laboratory, Tech. Rep. LA-UR-03-1987, 2003 [Google Scholar]
  12. J. Leppänen, M. Pusa, T. Viitanen, V. Valtavirta, T. Kaltiaisenaho, The Serpent Monte Carlo code: status, development and applications in 2013, Ann. Nucl. Energy 82, 142 (2015) [CrossRef] [Google Scholar]
  13. M.A. Kowalski, P. Cosgrove, J. Broman, E. Shwageraus, SCONE: a student-oriented modifiable Monte Carlo particle transport framework, J. Nucl. Eng. 2, 57 (2021) [CrossRef] [Google Scholar]
  14. B. Molnar, G. Tolnai, D. Legrady, A GPU-based direct Monte Carlo simulation of time dependence in nuclear reactors, Ann. Nucl. Energy 132, 46 (2019) [CrossRef] [Google Scholar]
  15. H. Lee, W. Kim, P. Zhang, M. Lemaire, A. Khassenov, J. Yu, Y. Jo, J. Park, D. Lee, MCS – a Monte Carlo particle transport code for large-scale power reactor analysis, Ann. Nucl. Energy 139, 107276 (2020) [CrossRef] [Google Scholar]
  16. K. Wang, Z. Li, D. She, J. Liang, Q. Xu, Y. Qiu, J. Yu, J. Sun, X. Fan, G. Yu, RMC – a Monte Carlo code for reactor core analysis, Ann. Nucl. Energy 82, 121 (2015) [CrossRef] [Google Scholar]
  17. J. L. Conlin, P. Romano, A Compact ENDF (ACE) format specification, Los Alamos National Laboratory, Tech. Rep. LA-UR-19-29016. [Online], 2019, Available: https://www.osti.gov/biblio/1561065 [Google Scholar]
  18. R. MacFarlane, A. Kahler, Methods for processing ENDF/B-VII with NJOY, Nucl. Data Sheets 111, 2739 (2010) [CrossRef] [Google Scholar]
  19. H. Belanger, Papillon Nuclear Data Library, v0.3.1. [Online], 2023, Available: https://github.com/HunterBelanger/papillon-ndl [Google Scholar]
  20. A. Scopatz, P.K. Romano, P.P. Wilson, K.D. Huff, PyNE: Python for nuclear engineering, Trans. Am. Nucl. Soc. 107, 985 (2022) [Google Scholar]
  21. P.K. Romano, N.E. Horelik, B.R. Herman, A.G. Nelson, B. Forget, K. Smith, OpenMC: a state-of-the-art Monte Carlo code for research and development, Ann. Nucl. Energy 82, 90 (2015) [CrossRef] [Google Scholar]
  22. ACEtk. [Online], Available: https://github.com/njoy/ACEtk [Google Scholar]
  23. N. Soppera, M. Bossant, E. Dupont, JANIS 4: an improved version of the NEA Java-based nuclear data information system, Nucl. Data Sheets 120, 294 (2014) [CrossRef] [Google Scholar]
  24. Y. Wang, E. Brun, F. Malvagi, C. Calvin, Competing energy lookup algorithms in Monte Carlo neutron transport calculations and their optimization on CPU and intel MIC architectures, Proc. Comput. Sci. 80, 484 (2016) [CrossRef] [Google Scholar]
  25. F. Brown, New hash-based energy lookup algorithm for Monte Carlo codes, Los Alamos National Laboratory, Tech. Rep. LA-UR-14-24530, 2014 [Google Scholar]
  26. L.B. Levitt, The probability table method for treating unresolved neutron resonances in Monte Carlo calculations, Nucl. Sci. Eng. 49, 450 (1972) [CrossRef] [Google Scholar]
  27. D.E. Cullen, C.R. Weisbin, Exact Doppler broadening of tabulated cross sections, Nucl. Sci. Eng. 60, 1999 (1976) [CrossRef] [Google Scholar]
  28. R. Coveyou, R. Bate, R. Osborn, Effect of moderator temperature upon neutron flux in infinite, capturing medium, J. Nucl. Energy 2, 153 (1956) [Google Scholar]
  29. A. Zoia, E. Brun, C. Jouanne, F. Malvagi, Doppler broadening of neutron elastic scattering kernel in Tripoli-4, Ann. Nucl. Energy 54, 218 (2013) [CrossRef] [Google Scholar]
  30. P.K. Romano, J.A. Walsh, An improved target velocity sampling algorithm for free gas elastic scattering, Ann. Nucl. Energy 114, 318 (2018) [CrossRef] [Google Scholar]
  31. W. Rothenstein, Neutron scattering kernels in pronounced resonances for stochastic Doppler effect calculations, Ann. Nucl. Energy 23, 441 (1996) [CrossRef] [Google Scholar]
  32. B. Becker, R. Dagan, G. Lohnert, Proof and implementation of the stochastic formula for ideal gas, energy dependent scattering kernel, Ann. Nucl. Energy 36, 470 (2009) [CrossRef] [Google Scholar]
  33. J.L. Conlin, W. Haeck, D. Neudecker, D.K. Parsons, M.C. White, Release of ENDF/B-VIII.0-Based ACE data files, Los Alamos National Laboratory, Tech. Rep. LA-UR-18-24034, 2018 [CrossRef] [Google Scholar]
  34. D.K. Parsons, C.A. Toccoli, Re-release of the ENDF/B VIII.0 S(α, β) data processed by NJOY2016, Los Alamos National Laboratory, Tech. Rep. LA-UR-20-24456, 2020. [Google Scholar]
  35. W. Haeck, J.L. Conlin, A.P. McCartney, A.C.I. Kahler, NJOY2016 updates for ENDF/B-VIII.0, Los Alamos National Laboratory, Tech. Rep. LA-UR-18-22676, 2018. [CrossRef] [Google Scholar]
  36. H. Belanger, MGMC v0.3.0. [Online], 2022, Available: https://github.com/HunterBelanger/mgmc [Google Scholar]
  37. H. Belanger, Development of numerical methods for neutronics in continuous media, Ph.D. dissertation, Université Paris-Saclay, 2022 [Google Scholar]
  38. J. Paratte, R. Früh, U. Kasemeyer, M. Kalugin, W. Timm, R. Chawla, A benchmark on the calculation of kinetic parameters based on reactivity effect experiments in the CROCUS reactor, Ann. Nucl. Energy 33, 739 (2006) [CrossRef] [Google Scholar]
  39. M. Chadwick, P. Obložinský, M. Herman, N. Greene, R. McKnight, D. Smith, P. Young, R. MacFarlane, G. Hale, S. Frankle, A. Kahler, T. Kawano, R. Little, D. Madland, P. Moller, R. Mosteller, P. Page, P. Talou, H. Trellue, M. White, W. Wilson, R. Arcilla, C. Dunford, S. Mughabghab, B. Pritychenko, D. Rochman, A. Sonzogni, C. Lubitz, T. Trumbull, J. Weinman, D. Brown, D. Cullen, D. Heinrichs, D. McNabb, H. Derrien, M. Dunn, N. Larson, L. Leal, A. Carlson, R. Block, J. Briggs, E. Cheng, H. Huria, M. Zerkle, K. Kozier, A. Courcelle, V. Pronyaev, S.V.D. Marck, ENDF/B-VII.0: next generation evaluated nuclear data library for nuclear science and technology, Nucl. Data Sheets 107, 2931 (2006) [CrossRef] [Google Scholar]
  40. A. Zoia, Y. Nauchi, E. Brun, C. Jouanne, Monte Carlo analysis of the CROCUS benchmark on kinetics parameters calculation, Ann. Nucl. Energy 96, 377 (2016) [CrossRef] [Google Scholar]
  41. C.T. Ballinger, The direct S(α, β) method for thermal neutron scattering, in Proceedings of the International Conference on Mathematics and Computations, Reactor Physics, and Environmental Analyses (1995), Vol. 1, pp. 134–143. [Google Scholar]
  42. X.-X. Cai, T. Kittelmann, E. Klinkby, J.M. Damián, Rejection-based sampling of inelastic neutron scattering, J. Comput. Phys. 380, 400 (2019) [CrossRef] [Google Scholar]

Cite this article as: Hunter Belanger. Papillon Nuclear Data Library – a free and open-source C++/Python library for interacting with ACE files for continuous-energy neutron data, EPJ Nuclear Sci. Technol. 9, 23 (2023)

All Figures

thumbnail Fig. 1.

Example Jupyter notebook using PapillonNDL’s Python API to compare elastic scattering for a 36.25 eV neutron sampled using both SVT and DBRC off of 238U.
In the text
thumbnail Fig. 2.

Comparison of PapillonNDL and OpenMC for an Uncorrelated scattering distribution, using a Maxwellian spectrum for energy. The demonstrated distribution is for 241Pu MT18, at an incident energy of eV. The p-values for the energy and angle distributions are 0.496 and 0.548 respectively.
In the text
thumbnail Fig. 3.

Comparison of PapillonNDL and OpenMC for a Kalbach-Mann scattering distribution. The demonstrated distribution is for 16O MT28, at an incident energy of 20 MeV. The p-values for the energy and angle distributions are 0.962 and 0.159 respectively.
In the text
thumbnail Fig. 4.

Comparison of PapillonNDL and OpenMC for a Tabular Energy-Angle scattering distribution. The demonstrated distribution is for 235U MT16, at an incident energy of 10 MeV. The p-values for the energy and angle distributions are 0.446 and 0.513 respectively.
In the text
thumbnail Fig. 5.

Comparison of PapillonNDL and OpenMC for an NBody scattering distribution. The demonstrated distribution is for 2H MT16, at an incident energy of 10 MeV. The p-values for the energy and angle distributions are 0.373 and 0.341 respectively.
In the text
thumbnail Fig. 6.

Comparison of PapillonNDL and OpenMC implementation of elastic scattering with DBRC. The demonstrated distribution is for 238U at 293.6 K and incident energy of 36.26 eV. The p-values for the energy and angle distributions are 0.666 and 0.927 respectively.
In the text
thumbnail Fig. 7.

Comparison of PapillonNDL and OpenMC for an incoherent inelastic scattering with 1H in water at 293.6 K, and at an incident energy of 0.99 eV. The p-values for the energy and angle distributions are 0.806 and 0.875 respectively.
In the text
thumbnail Fig. 8.

Flux profile for the CROCUS research reactor at EPFL, simulated using the Chenille Monte Carlo mini-app, with PapillonNDL for continuous-energy neutron physics.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.