| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
Special Issue on 4th International Workshop on Nuclear Data Covariances, October 2–6, 2017, Aix en Provence, France – CW2017
|
|
|---|---|---|
| Article Number | 37 | |
| Number of page(s) | 6 | |
| Section | Covariance Evaluation Methodology | |
| DOI | https://doi.org/10.1051/epjn/2018037 | |
| Published online | 14 November 2018 | |
https://doi.org/10.1051/epjn/2018037
Regular Article
Covariance analysis for total neutron cross sections based on a microscopic optical model potential
China Nuclear Data Center, China Institute of Atomic Energy,
P.O. Box 275(41),
Beijing
102413, P.R. China
* e-mail: xrr-001@163.com
Received:
7
December
2017
Received in final form:
1
March
2018
Accepted:
28
May
2018
Published online: 14 November 2018
The deterministic simple least square (LS) approach is employed in the covariance analysis of the total neutron cross section (n,tot) calculated by a microscopic optical potential, CTOM, which is based on a fundamental theory − Dirac Brueckner Hartree Fock. The sensitivity to the CTOM parameters is firstly systematically calculated for 77 stable nuclei in the range 12C–208Pb within neutron energy 5–200 MeV. Then, an equivalent covariance of experimental data (EVexp) is constructed to describe the experimental data uncertainties and the systematic difference between experimental data and CTOM calculation. The variance and covariance of EVexp matrix are both evaluated via the Gaussian analysis to the ratios of measured (n,tot) cross sections and the CTOM calculations. In addition, a technique named “selection of effective points (SEP)” is suggested additionally to reduce the influence of the Peelle's Pertinent Puzzle problem in this work.
© R. Xu et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
As well known, covariance of cross sections make a big impact on the target accuracy design of modern nuclear facilities such as the reactors of Generation-IV [1]. Because experimental data on stable or unstable nuclei can be lacking for modern nuclear engineering studies, the evaluation of these nuclear data must rely heavily on theoretical calculations. Therefore, how to derive cross sections and associated covariance out of theoretical results is an attractive issue in the study of nuclear data.
The research based on a fundamental theory with better background and less freedom is believed to provide more confidence in theoretical prediction. Recently, a microscopic optical potential, CTOM, based on the Dirac Brueckner Hartree Fock (DBHF) theory has been developed in China Nuclear Data Center and Tuebingen University to globally describe the nucleon scattering from 12C–208Pb for nuclear energy in the range 5–200 MeV [2,3]. It is interesting to study the covariance of the CTOM predictions. Since CTOM is built on a microscopic theory, the covariance estimation should show some different features comparing to the traditional evaluation based on phenomenology. A very preliminary trial has been performed in reference [4] according to the uncertainty of the differential cross sections of nucleon scattering from 40Ca and 208Pb, however, due to its complexity, the covariance of the CTOM prediction still deserve to be further studied, namely for its impact on other physics observable. Therefore, the purpose of this article is to further explore the covariance according to another important observable, the cross sections of (n,tot), and discuss more performance of CTOM predictions.
The methodologies of covariance evaluation can be simply classified as the deterministic least square (LS) approach and the stochastic Monte Carlo approaches [5]. Both have been used in the real nuclear data evaluation. Considering the merits of LS approach, such as involving more details of the experimental data and less time consuming, it is adopted in this work to analyze the covariance obtained from CTOM predictions. At the same time, some special methods related to the parameter sensitivity, the experimental covariance, and the Peelle's Pertinent Puzzle (PPP) effect are discussed in LS according to the properties of microscopic CTOM prediction.
The scheme of CTOM and its predictions have been presented in reference [3], in this paper, we focus on introducing the whole covariance evaluation process. The content is organized as follows. Firstly, a general description is presented to describe the LS approach in Section 2. Then, the sensitivity with respect of the CTOM parameters [2] are discussed in Section 3. The calculated total neutron cross sections of 77 stable nuclei in the region 12C–208Pb are contained in this process, and a special parametrization for the uncertain components is designed to obtain the sensitivity. Thirdly, a so-called equivalent covariance of experimental data (EVexp) is introduced to describe the covariance based on the microscopic predictions and experimental data, which are illustrated in Section 4. In order to reduce the effect of PPP problem, we adopt a technique named “selection of effective points (SEP)” in LS calculation and the satisfactory result is presented in Sections 5 and 6. At last, this paper is summarized in Section 7.
2 The deterministic simple LS approach
Up to now, the LS approach is still very popular in the nuclear data and covariance evaluation. The conventional flow chart can be exhibited as Figure 1, and its full formalism can be referred in [6]. It is worthwhile to note that when assuming the prior probability of parameters of function f as 1, the LS approach can be expressed as the simple LS. It starts from an initial input of parameter array C0 and the initial derived values Y* by the function f. The relevant parameter sensitivity matrix F is calculated for every variable xi by the function f. After that, the parameter array C0 is replaced by the new modified 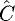 via the uncertainty propagation from the experimental covariance Wy and theoretical sensitivities F. The process above will be iterated until the conditions set in the left bottom in Figure 1 are satisfied. The obtained
via the uncertainty propagation from the experimental covariance Wy and theoretical sensitivities F. The process above will be iterated until the conditions set in the left bottom in Figure 1 are satisfied. The obtained 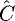 is believed to be the best estimate to fit the experimental data y and the parameters covariance matrix
is believed to be the best estimate to fit the experimental data y and the parameters covariance matrix 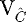 , the derived value
, the derived value 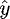 and the associated covariance
and the associated covariance 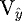 are obtained as shown in Figure 1. In order to make use of the LS approach in this work, several issues related to CTOM are specifically discussed in the following.
are obtained as shown in Figure 1. In order to make use of the LS approach in this work, several issues related to CTOM are specifically discussed in the following.
 |
Fig. 1 The flow chart of conventional LS approach. |
3 The sensitivity analysis
The sensitivity of model parameter F is one of the important components in LS, as mentioned in Section 2. It can exhibit the impact of uncertainties of the model parameter on the target function f, which is given by,
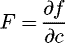 (1)
(1)
Normally, F can be calculated through the analytical or numerical solution according to the target function f. However, the target function in CTOM is based on the microscopic theory but not phenomenological expression with a lot of adjusted parameters, which make it a difficulty to derive the F matrix in the conventional way. In order to solve this problem, we focus on finding the uncertain sources in the CTOM by performing a discussion throughout its whole formula scheme.
As presented in references [2,3], CTOM potential is built based on the relativistic self-energies by DBHF calculation, ∑s, ∑0, ∑v, which represent the scalar part of self-energy, the time-like and space-like terms of the vector part, respectively. There is no free parameter in the solution procedure of nucleon self-energies within the nuclear matter. When the concentration is shifted to the finite nuclei, two uncertain parts are involved inevitably in the theoretical scheme of CTOM, namely the extrapolation of Dirac potentials Us, U0 at lower density and the effective interaction range parameter t in the improved local density approximation (ILDA). The sensitivity of t can easily been calculated through incorporating small perturbation to the optimized t values [3], but Us, U0 at lower density region are different, because there are not direct parameter expression for them. In our previous trial in [4], the sensitivity is calculated by making perturbation on the auxiliary potentials points at ρ = 0.04 fm−3 for the real parts and at ρ = 0.04 and 0.06 fm−3 for the imaginary parts, which are used in the Us and U0 extrapolation in the “full” density region for finite nuclei. In order to make more direct calculation, we introduce a simple quadratic curve f1 as function of the nuclear matter density ρ with the maximum of amplitude F0 at ρ = ρ0 while ρ varies in [0, 0.08], F0 indicates the amplitude of perturbation in sensitivity calculation,
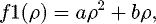 (2)
where
(2)
where
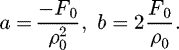 (3)
(3)
We define f(ρ) = 1 + f1(ρ), and the real and imaginary parts of Dirac potentials at lower density can be parameterized as
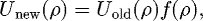 (4)
where Uold stands for the original Us and U0 of CTOM. In this work, we select ρ0 = 0.04 fm−3 and set |F0|≪1 to keep Unew as a tiny deviation from the Uold, which is required in the numerical solution of sensitivity. It is known that the step length is the important factor to derive the correct sensitivity in the numerical solution to equation (1). In this work, F0 in equation (3) is adopted as 0.035 for all U potentials, the f, f 1 and relevant perturbation to Dirac potentials are shown in Figures 2 and 3. The absolute value of F0 is set to 0.2, in Figure 2 “minus” stands for F0 = − 0.2 and “plus” for F0 = 0.2. The corresponding change is propagated to the Dirac potentials as shown in Figure 2. The sensitivities are calculated based on this parameter variation. In addition, the variation step for the factor “t ” is taken as Δt = 0.01t all calculations in ILDA as in references [3,4].
(4)
where Uold stands for the original Us and U0 of CTOM. In this work, we select ρ0 = 0.04 fm−3 and set |F0|≪1 to keep Unew as a tiny deviation from the Uold, which is required in the numerical solution of sensitivity. It is known that the step length is the important factor to derive the correct sensitivity in the numerical solution to equation (1). In this work, F0 in equation (3) is adopted as 0.035 for all U potentials, the f, f 1 and relevant perturbation to Dirac potentials are shown in Figures 2 and 3. The absolute value of F0 is set to 0.2, in Figure 2 “minus” stands for F0 = − 0.2 and “plus” for F0 = 0.2. The corresponding change is propagated to the Dirac potentials as shown in Figure 2. The sensitivities are calculated based on this parameter variation. In addition, the variation step for the factor “t ” is taken as Δt = 0.01t all calculations in ILDA as in references [3,4].
As a result, six parameters in total are considered in describing the uncertainties in CTOM, they are t-Re, t-Im in ILDA and Real Us and U0 (ReUs, ReU0), Imaginary Us, U0 (ImUs, ImU0) respectively. Figure 4 shows the calculated sensitivities for the 12C(n,tot) cross sections in 5 ≤ En ≤ 200 MeV. One can observe that 12C(n,tot) cross sections are sensitive to ReUs, ReU0, ImUs, t-Re, and the sensitivities of ReUs and ReU0 vary with energies more significantly.
In our calculation, the sensitivities have been derived for 77 stable nuclei in 12C–208Pb in the incident energy region 5–200 MeV. The cross sections below 5 MeV are not involved in this analysis due to the complex structures in (n,tot) cross section curves especially in the unresolved resonance region, whose structures can not be reproduced by optical model. We assemble the sensitivity results of 12C–208Pb in one sensitivity matrix in our LS calculation. 77 nuclei in total are contained in this analysis, and they are 12C, 14N, 16O, 19F, 20Ne, 23Na, 24Mg, 27Al, 28Si, 31P, 32S, 35Cl, 40Ar, 39K, 40Ca, 45Sc, 48Ti, 51V, 52Cr, 55Mn, 56Fe, 59Co, 58Ni, 63Cu, 66Zn, 69Ga, 74Ge, 75As, 80Se, 79Br, 84Kr, 85Rb, 88Sr, 89Y, 90Zr, 93Nb, 96Mo, 99Tc, 102Ru, 103Rh, 106Pd, 107Ag, 112Cd, 115In, 120Sn, 121Sb, 128Te, 127I, 132Xe, 133Cs, 138Ba, 139La, 140Ce, 141Pr, 144Nd, 147Pm, 152Sm, 153Eu, 160Gd, 159Tb, 164Dy, 165Ho, 166Er, 169Tm, 174Yb, 175Lu, 180Hf, 181Ta, 184W, 187Re, 192Os, 193Ir, 195Pt, 197Au, 202Hg, 205Tl, 208Pb, respectively.
 |
Fig. 2 The curves of perturbation function f 1 and f at ρ ≤ 0.08 fm−3. |
 |
Fig. 3 The perturbation for Us and U0 in this work. |
 |
Fig. 4 The sensitivities of six parameters to the 12C(n,tot) cross sections. |
4 The equivalent covariance of experimental data
It is well known that the experimental data are important in LS to obtain the optimized parameters of the target function, and the experimental covariance matrix (Wy), as shown in Figure 1, also plays an important role to provide the weights of the each experimental data point in the fitting process. In this work, we introduce a so-called EVexp instead of the classical one to incorporate the experimental information in the covariance evaluation for CTOM. EVexp is mainly constructed through exploring the systematic deviation between experimental data and the theoretical results, and the systematic evaluation of the total uncertainties of experimental data for 12C–208Pb. In total, more than 3000 sets of measurements for (n,tot) cross sections are involved, and the neutron incident energies En are ranging from 5–200 MeV.
In order to evaluate the EVexp matrix, we firstly define three uncertainties: ERR1, ERR2 and ERR3. In our estimation, ERR1 is the uncorrelated (statistical) uncertainty and comes directly from the reported total error of experimental data. As shown in Figure 5, we analyze all measured points in the 3000 sets of experimental data, each point is taken as one statistic sample in EVexp. A systematics function is obtained to evaluated the uncertainties for 12C–208Pb in Figure 5. This uncertainty is taken as the statistic uncertainty ERR1.
In our correlated uncertainty estimation, the statistic Gaussian analysis is used to evaluate the ratio = E/C, namely the ratio of measurements “E” and theoretical results “C”, to obtain the correlation. In order to get the better description to the E/C, we separate the analysis into two energy regions, 5–20 MeV and 20–200 MeV. Figure 6 shows the Gaussian analysis results for the E/C in 20–200 MeV. The FWHM of Gauss curve indicates the correlated uncertainty, ERR2 = 0.026 in 20–200 MeV, and the deviation between the Gauss curve center and 1.0 is the correlated uncertainty ERR3 = 0.038 in 20–200 MeV. In our work, ERR2 is adopted as the middle-range correlation in 20–200 MeV, and ERR3 is taken as the long-range correlation not only in 20–200 MeV but also between 20–200 MeV and 5–20 MeV, because it reflects the systematic deviation between measurements and theory predictions to some extend.
Based on the evaluation above, the matrix element ρij (correlation) in EVexp is built through the following formula,
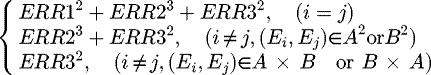 (5)
where “A” and “B” stand for the energy regions of 5–20 MeV and 20–200 MeV, respectively. It is noted that the coefficient of correlated uncertainties between different energies are preliminarily assumed as 1.0 in our calculation.
(5)
where “A” and “B” stand for the energy regions of 5–20 MeV and 20–200 MeV, respectively. It is noted that the coefficient of correlated uncertainties between different energies are preliminarily assumed as 1.0 in our calculation.
 |
Fig. 5 The systematics study of the measured uncertainties of 12C–208Pb(n,tot) cross sections. |
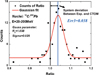 |
Fig. 6 The Gaussian analysis to the counts of ratio in 20–200 MeV. |
5 The technique to reduce influence from Peelle's Pertinent Puzzle problem
It is known that PPP problem is the inevitable issue when linear assumption is used to evaluate the nonlinear response function [7]. In order to reduce the PPP effect, we employ a method named SEP in our scheme. In SEP, the Gaussian analysis is also employed to pick out the proper points from the huge experimental database of the 12C–208Pb(n,tot) cross sections. The adopted samples of experimental data used in LS are restricted to the data whose values are consistent with the theoretical prediction within 1 sigma. 27Al(n,tot) is chosen to illustrate the results of SEP in Figure 7. One can observe that the data derived from LS with SEP (red curve) is obviously improved and closer to the CTOM results (blue curve) and remains consistent with the measurements, while the one without SEP (black curve) is rather apart from others.
 |
Fig. 7 The comparison of CTOM calculation, the derived cross sections with and without SEP approach in LS, and the experimental data of 27Al(n,tot). |
6 The derived covariance for prediction of CTOM
After combining the experimental and theoretical uncertainties using the sensitivity F, EVexp and SEP approach in LS, we derive the covariance of CTOM predictions. As an example, the 27Al(n,tot) cross sections with derived uncertainties are shown in Figure 7 and the covariance (correlation) is shown in Figure 8. Labels of X-axis and Y-axis in Figure 8 are both energy mesh-grids from 5–200 MeV. In this work, the reduced χ2 is defined to assess the quality of LS results,
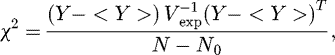 (6)
where N indicates the dimension of covariance of experimental data, and N0 is the number of parameters in CTOM. The LS outputs are finally adopted when the derived cross-section curve is almost equivalent to the CTOM calculation. In this case, χ2 equals to 0.98, which is close to 1.0 and indicates that the present LS results remains in good agreement with the experimental data within the uncertainty band, as shown in Figure 7.
(6)
where N indicates the dimension of covariance of experimental data, and N0 is the number of parameters in CTOM. The LS outputs are finally adopted when the derived cross-section curve is almost equivalent to the CTOM calculation. In this case, χ2 equals to 0.98, which is close to 1.0 and indicates that the present LS results remains in good agreement with the experimental data within the uncertainty band, as shown in Figure 7.
In addition, the parameters covariance matrix (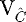 ) is derived simultaneously with other outputs in LS, and the covariance of CTOM predictions of any nuclide scares of measurements can also be produced in our approach.
) is derived simultaneously with other outputs in LS, and the covariance of CTOM predictions of any nuclide scares of measurements can also be produced in our approach.
 |
Fig. 8 The correlation matrix of the 27Al(n,tot) cross sections. |
7 Conclusion
In this work, the LS approach is applied to evaluate covariance data related to the (n,tot) cross sections by the nucleon-nucleus microscopic optical model CTOM. According to its application scope, the current covariance evaluation contains the analysis to 12C–208Pb in the range 5–200 MeV. Considering the features of CTOM, the covariance is obtained through combining the information from theoretical predictions and experimental data by LS. Moreover, through this covariance analysis, the CTOM is further been proved to be powerful in the nucleon-nucleus scattering calculation, and the current scheme can be used to generate the covariance of (n,tot) cross sections predicted by CTOM for any nuclei of interest.
Author contribution statement
In this work, the covariance evaluation scheme was derived by Ruirui Xu, Tingjin Liu and Zhigang Ge, and the entire calculation and analysis was performed by Ruirui Xu and Zhi Zhang. The experimental data of total neutron cross sections were collected comprehensively and pre-evaluated by Zhang Yue and Xi Tao.
Acknowledgments
This work has been supported by the National Natural Science Foundation of China (Grant Nos. U1630143); We thank Prof. Z.Y. Ma, Prof. H. Muether and Prof. Q.B. Shen for their kindly discussions on CTOM calculation and covariance evaluation.
References
- G. Palmiotti, M. Assawaroongruengchot, M. Salvatores et al., J. Korean Phys. Soc. 59, 1264 (2011) [CrossRef] [Google Scholar]
- R. Xu, Z. Ma, E.N.E. Van Dalen et al., Phys. Rev. C 59, 034613 (2012) [CrossRef] [Google Scholar]
- R. Xu, Z. Ma, Y. Zhang et al., Phys. Rev. C 94, 034606 (2016) [CrossRef] [Google Scholar]
- R. Xu, Z. Ma, H. Muether et al., EPJ Web Conf. 146, 12009 (2017) [CrossRef] [Google Scholar]
- D.L. Smith, Am. Nucl. Soc., LaGrange Park, IL, USA (1991) [Google Scholar]
- D.L. Smith et al., ANL/NDM-128 (1993) [Google Scholar]
- A.D. Carlson, V.G. Pronyaev, D.L. Smith et al., Nucl. Data Sheets 110, 3215 (2009) [CrossRef] [Google Scholar]
Cite this article as: Ruirui Xu, Zhigang Ge, Tingjin Liu, Yue Zhang, Xi Tao, Zhi Zhang, Covariance analysis for total neutron cross sections based on a microscopic optical model potential, EPJ Nuclear Sci. Technol. 4, 37 (2018)
All Figures
 |
Fig. 1 The flow chart of conventional LS approach. |
| In the text | |
 |
Fig. 2 The curves of perturbation function f 1 and f at ρ ≤ 0.08 fm−3. |
| In the text | |
 |
Fig. 3 The perturbation for Us and U0 in this work. |
| In the text | |
 |
Fig. 4 The sensitivities of six parameters to the 12C(n,tot) cross sections. |
| In the text | |
 |
Fig. 5 The systematics study of the measured uncertainties of 12C–208Pb(n,tot) cross sections. |
| In the text | |
 |
Fig. 6 The Gaussian analysis to the counts of ratio in 20–200 MeV. |
| In the text | |
 |
Fig. 7 The comparison of CTOM calculation, the derived cross sections with and without SEP approach in LS, and the experimental data of 27Al(n,tot). |
| In the text | |
 |
Fig. 8 The correlation matrix of the 27Al(n,tot) cross sections. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


