| Issue |
EPJ Nuclear Sci. Technol.
Volume 4, 2018
|
|
|---|---|---|
| Article Number | 18 | |
| Number of page(s) | 8 | |
| DOI | https://doi.org/10.1051/epjn/2018040 | |
| Published online | 19 September 2018 | |
https://doi.org/10.1051/epjn/2018040
Regular Article
Reflector features and physics consideration issued from the Jules Horowitz Reactor design analyses
Safety and Power Plant Process, Neutronic − Shielding − Criticality Department, TechnicAtome,
Aix-en-Provence, France
* e-mail: edwin.privas@technicatome.com
Received:
16
June
2017
Received in final form:
28
November
2017
Accepted:
31
May
2018
Published online: 19 September 2018
Mechanic solicitations induced by neutron and photon interactions have to be featured for components lifespan determination. TechnicAtome is in charge of both the design and building on behalf of CEA of the 100 MW Jules Horowitz Reactor (JHR). This modular Material Testing Reactor is under construction in southern France, with radioisotope production and material testing capabilities. Inner core components have been designed based on mechanical and thermohydraulic considerations. Both studies require neutronic physical quantities like the neutron flux and deposited energies. The JHR reflector is outside the primary loop and is composed of beryllium. Gamma shields are partially positioned between the reflector and the core to reduce photon heating on aluminum structures. The design is completed and this paper deals with the neutronic and photonic impacts on the reflector. A Monte Carlo methodology based on the MCNP code was developed to model the reactor and enhance fluxes and energy deposited maps. MCNPs mesh options are used over the detailed geometry model. The convolution with mechanical meshes enables to determine neutronic parameters on local structures, material by material. Time required for such modeling is very long if one requires results on every mesh with a maximum uncertainty of 2% (1σ). To reduce time calculation by a factor 3.5 on refined meshes, MCNP biasing methods have been used. Spatial distribution of the gamma heating shows the importance of the interface with the surrounding area. For example, photon and neutron interactions close to the gamma shield create numerous photons with lower energy adding heating at the shield interfaces. In order to keep high flux in the experimental part of the reflector, gamma shields are not continuously set around the reactor vessel. Consequently, some photon leakage arises in the reflector area, with limited impact on aluminum structures. The overall thermal flux map shows local effects and gradients that have to be taken into account by the physics studies. Material swellings are deduced from the fluxes on all reflector structures.
© E. Privas and L. Chabert, published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Design and development of new research reactor like Material Testing Reactors is mainly driven by the materials qualification, the fuel behavior characterization during nominal conditions or accident scenarios and the radioisotope production. In this scope, the Jules Horowitz Reactor (JHR) is intended to be a multipurpose research reactor with the largest experimental capacity in Europe [1]. One application will be to validate components both for the current nuclear reactors of second and third generations and for the next generation, thanks to high neutron flux (both in thermal and fast range and each around 5 × 1014 n·cm−2·s−1). Experimental devices like ADELINE, MADISON or MOLFY for 99Mo production are designed by CEA [2] and can be placed in serval part of the reactor. JHR is designed by TechnicAtome to fulfill the flux and maximum heating requirement of such experimental devices. HORUS V2.1 [3] chained with MCNP [4] are used to compute neutronic physical quantities for thermohydraulic and mechanical analysis [5].
This paper focuses on the main reflector features and neutronic methodology. Fine flux and heating distribution over the reflector will be discussed, leading to key design parameters. A special care will be given to the gamma shield and physics happening around. Finally, a mechanical application using heating and flux will be presented, showing the swelling of a sector.
2 Jules Horowitz Reactor
JHR is a 100 MW pool-type Material Testing Reactor cooled by light water. The core rack is a 60 cm height cylinder made of aluminum in which 37 drilled holes can host 34 fuel elements and three large devices. Every fuel assembly is composed of 8 cylindrical and concentric plates hold together with three stiffeners. A U3-Si2 metallic fuel is considered for this study. A 3 cm height Al-B poisoned insert positioned 1 cm above the top of each plate aims at limiting the flux upwelling and heat deposition above the fissile zone. This is mandatory because the water is warmer and less pressurized in this zone inducing lower vaporization margin.
Seven small test locations, called “simple DEN”, are placed in the center of the cylindrical fuel plates in order to have high fast flux. The other fuel elements are filled with hafnium rods to handle reactor reactivity both to provide depletion compensation and to ensure safety shutdowns. They are geometrically composed of two concentric hafnium tubes and an aluminum follower.
The core is surrounded with an aluminum vessel (containing the primary circuit) and then a reflector. The latter is mainly composed of beryllium elements, allowing a suitable thermal neutron flux for several material tests and 99Mo production. Neutrons coming from the inner core undergo more collisions in beryllium than water, with less absorption and a lower energy decrease by collision. It gives JHR higher experimental flexibility. In this paper, the experimental configuration considers 12 ADELINE devices type (called “PWR DEN”), consisting of UO2 1% 235U enriched fuel pin.
A zircaloy shield between core and reflector is set partially around the core to reduce gamma heating in some area.
The JHR neutronic model is described in Figures 1 and 2. Each reflector area is defined by a sector number and constitutes a mechanical entity. Only C1P1C6 are linked together.
 |
Fig. 1 JHR general description. Sectors name is given within orange boxes. Grey is for beryllium, blue for water, purple for aluminum, turquoise blue for zircaloy and orange for NaK. |
 |
Fig. 2 Core components description view. Grey is for beryllium, blue for water, purple for aluminum, turquoise blue for zircaloy and orange for NaK. |
3 Neutronic computational model and methodology
Different neutronic calculation codes are available at TechnicAtome to design the JHR: the determinist tools HORUS [3], the Monte Carlo transport code MCNP-6.1 [4], TRIPOLI-4® [6], Serpent-2 [7] and Geant4 [8]. The reflector design, because of its complex geometry, is performed using stochastic codes.
Moreover, MCNP is chosen because of a need to use specific options like biasing technics coupling with sur-imposed mesh. The nuclear data used in this paper is ENDF-VI.8 [9] with the photonic library coming from Lawrence Livermore Nuclear Laboratory (EPDL-92) [10].
The core and fuel burnup taken into account for this study correspond to a Beginning Of Cycle (BOC) at equilibrium sate. The material balance comes from HORUS-V2.1 by simulating a build up from the first cycle to the equilibrium state, following a specific fuel reshuffling strategy.
3.1 MCNP
Monte Carlo computer code, like MCNP, is a very powerful and versatile tool for particle transport calculations. It can be used for neutron and photon transport which is interesting for a reactor physicist who designs and optimizes a reactor. This code is used for calculations of multiplication factor, reaction rates, neutron fluxes, power peaking factors, neutronic and gamma heating. MCNP also provides multiple standard results types called “tallies”. Every output is normalized to one fission neutron in a critical calculation (using KCODE). In order to normalize the result by the thermal power of a system, scaling factors should be used (methodology is described in Sect. 3.2).
The “FMESH” convenient option of MCNP is used in this paper. It enables to quickly mesh an entire shape, allowing the user to describe a mesh independent of the modelled geometry. The “FMESH” card is associated to a “FM” card to transform the flux into heat deposition.
3.2 Results normalization
In MCNP, the easiest way to calculate the multiplication factor and physical quantities is through KCODE card (critical calculation). Since MCNP results are normalized to one neutron fission source, they have to be properly scaled in order to get absolute values. The scaling factor is calculated for a given power level. The normalized factor is calculated by using directly the “loss to fission” results given in the MCNP output and the total heating in the vessel:
 with fn, flux normalisation factor; PCore, core power; C, eV-J conversion factor; Wfiss, energy produced per fission; τf, fission rate;
with fn, flux normalisation factor; PCore, core power; C, eV-J conversion factor; Wfiss, energy produced per fission; τf, fission rate;  , neutron heating deposited within the vessel;
, neutron heating deposited within the vessel;  , prompt gamma heating deposited within the vessel;
, prompt gamma heating deposited within the vessel;  , prompt beta heating deposited;
, prompt beta heating deposited;  , delayed gamma heating deposited within the vessel coming from fission product.
, delayed gamma heating deposited within the vessel coming from fission product.
 ,
, 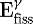 and τf are calculated using two FMESH containing the primary circuit. The option “FM −1 0 −4 1” for gamma heating and “FM −1 0 −5 −6” for neutron heating enables to get the induce energy deposition in all materials within the mesh. MCNP chosen model does not calculate directly the delayed gamma heating deposited within the vessel
and τf are calculated using two FMESH containing the primary circuit. The option “FM −1 0 −4 1” for gamma heating and “FM −1 0 −5 −6” for neutron heating enables to get the induce energy deposition in all materials within the mesh. MCNP chosen model does not calculate directly the delayed gamma heating deposited within the vessel 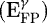 . It is evaluated proportionally (bdg = 36%) to the prompt gamma heating
. It is evaluated proportionally (bdg = 36%) to the prompt gamma heating  as:
as:
 Finally, the flux renormalisation is given by:
Finally, the flux renormalisation is given by:
 with
with  , mean neutronic heating deposited inside the vessel calculated by MCNP;
, mean neutronic heating deposited inside the vessel calculated by MCNP; 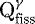 , mean gamma prompt heating deposited inside the vessel calculated by MCNP.
, mean gamma prompt heating deposited inside the vessel calculated by MCNP.
For neutron heating, the normalization factor becomes C ⋅ fn.
For gamma heating, the normalization factor becomes C ⋅ fn (1 + bdg). No nuclear data biases are considered in this paper but are taken into account for design studies.
3.3 Weighing method
With the objective to obtain finest values in the reflector area, the weight window generator capability of MCNP is chosen. The option is mandatory to converge below an uncertainty of 5% at 2σ on a fine cylindrical mesh, as describe in Section 4.1.
The mesh-based weight window method is used to both increase sampling in important regions of interest and to control particle weights. Upper and lower weight bounds are assigned to each region of phase space. Particles with weights above the bounds are split in two particles with a weight divided by a factor two. Particles with weights below the bounds are rouletted so that those that survive have weights increased. The weight decreases in the direction of importance and increases away from important regions. As a result, many lower weight particles reach the regions of importance.
Figure 3 explains the weight window principle and shows a neutron flux weight map created by the MCNP generator.
In the JHR reflector case, the declared region of importance is located in an outside rim, in order to attract particles from the inner core. More precisely, two weight maps are generated: one for fast neutron flux (>0.1 MeV) and another one for gamma heating. For instance, to produce the neutron weighting map, the following energy grid is taken: 0.625E-6 0.1 5 20. Those parameters were selected to:
split very fast neutron from the core because they will contribute directly to the area of interest;
split and deal with neutron slowdown in the reflector, for neutron between 0.1 MeV to 5 MeV;
kill with a Russian roulette thermal neutron coming from the core under 0.1 MeV;
optimize the map to converge either on thermal flux and fast flux for different materials.
The time gained on a calculation is estimated at about 3.5. The weighting maps are used at different burnup steps. It is justified because the same geometry is taken into account (only control rods are withdrawn) and only one mesh is used in the core to avoid an incoherent biasing.
 |
Fig. 3 Weight ponderation scheme on the left and neutron flux weight map obtained with the MCNP generator on the right, for neutron energy from 5 MeV to 20 MeV. |
4 Discuss on neutronic results
4.1 Total heating distribution
FMESH options in MCNP are used to get neutronic and gamma heating distribution in the reflector. The fine mesh is given in Figure 4. Details are given in Table 1.
FMESH is a tally flux based. It is possible to use a “FM” card, as described in Section 3.2, to obtain neutron and photon energy deposition. Two options are commonly used: either a virtual material for all the map, usefull for mechanical application because it is possible to interpolate correctly the physical quantities, or the “FM0” option considering effective materials. The latter option gives a good idea of the real distribution, as it can be seen in Figure 5. The neutron energy deposition is azimutaly uniform. Maximum deposition are closed to the pressure vessel, especially in the gamma shield and in the fuel pins in reflector devices (12 red points), explained by the fission occurring caused by a high termal flux.
Nevertheless neutron heating in reflector is, by a factor 5, lower than gamma heating. The effect of the gamma shield is clearly identified, with a fast decrease. It is explained because zirconium has 40 electrons, much more than other materials around, inducing much more interaction with photons. The mean efficiency of the gamma shield has been evaluated by calculating the average ratio difference between energy deposition before and after the gamma shield. This factor is about 1.75.
 |
Fig. 4 Fine mesh used for distribution map. |
Mesh options.
 |
Fig. 5 Neutron heating on the left and gamma heating on the right. The values are taken in the axial center of the core, integrated axially over 5 cm. Neutron heating in reflector is, by an average factor 5, lower than gamma heating (different color scale). |
4.2 Focus on the gamma shield in P1
A more detailed map has been produced for gamma shield. For convenience, only the P1 is considered in this section along the x axis. Total heating (coming mainly from gamma energy deposited in zirconium) decreases radially in the shield. Meanwhile, the exponential slope stops when reaching the interface with the reflector, as shown in Figure 6. This change is explained by gamma interactions in beryllium, where Compton Effect is happening. Indeed, Figure 7 shows three different curves to quantify the beryllium contribution. A first curve (in blue dot) represents the gamma spectrum in zircaloy close to the core. The green curve illustrates what is happening at the shield interface with the beryllium. Finally, a simulation (orange line) with void instead of beryllium and structures shows the difference in term of contribution and how much photon is produced by Compton for energy below 1 MeV.
Figure 8 shows the classical graph giving approximately the dominant interaction according to the incident photon energy. In beryllium (Z = 4), Compton Effect is the dominant interaction. Beryllium can then be seen as a secondary photon source. More details are given in Figure 9, where the photon spectrum coming from beryllium only has been isolated. A first curve (in black) represents the Compton gamma heating contribution (it means photons created by Compton Effect in the beryllium which deposit their energy in the shield). The three other curves show the absolute contribution depending on the photon origin (interactions in beryllium). One can notice the electron-positron annihilation simulated by MCNP with a gamma peak at 511 keV. This peak contributes to less than 10% of the total gamma heating below 1 MeV.
Similar physics and interpretations can be performed azimutaly. The main contribution is the Compton Effect coming from aluminum and photon leaks letting gamma shield borders be targeted by both core and reflector sources.
 |
Fig. 6 Total heating in the gamma shield of P1 sector (along × abscise). An increase of the energy deposition is found at the interface with the beryllium. |
 |
Fig. 7 Photonic spectrum taken at the internal and external gamma shield interface. |
 |
Fig. 8 Dominant gamma interactions depending on the incident gamma energy and the proton number of the target. |
 |
Fig. 9 Photonic spectrum taken at the internal and external gamma shield interface. |
4.3 Thermal flux distribution
Figures 10 and 11 show respectively the thermal flux distribution map (E < 0.625 eV) and an azimuthal extract for R = 38.6 cm, close to the pressure vessel. Maximum values are found in sector C2, which MOLFY samples will be held. In this area, four peaks appear and correspond to the four beryllium tables. Also, a high thermal flux is found in this location for three reasons:
at BOC, control rods are withdrawn in this reactor part, making an artificial “balance”;
during fuel reshuffling, fresh fuels are placed close to C2 sector;
thin water gap after the pressure vessel contributes to efficiently slow down fast neutrons without absorbing. Meanwhile, neutrons coming back from beryllium area will mainly be capture by the water, explaining thermal flux decrease where more water is found between tables.
 |
Fig. 10 Thermal flux distribution. Values are taken in the axial center of the core, integrated axially over 5 cm. |
 |
Fig. 11 Azimuthal flux distribution for a radius of 38.6 cm, close to pressure vessel and crossing mainly water and aluminum structures. |
5 Outlook
The previous results mentioned in this paper are supposed to be used as a dataset for mechanical studies. Then, neutronic distribution maps are interpolated over mechanical structure meshes with the use of ANSYS [11] format.
Firstly, neutron flux (fast and thermal) is integrated over lifetime to estimate a fluence map. It is used in irradiation-induced swelling law for aluminum and beryllium structures. Then, thermal power mainly produced by gamma heating is used with cooling conditions to evaluate structural temperature and dilatation. Some illustrations (Figs. 12 and 13) of swelling load (due to fluence) and total heating in P5 sector are shown for aluminum structures. Because every sector is fixed radially at both ends, swellings and heating will produce deformations and stresses, given in Figure 14. Deformations should be as low as possible in order to prevent obstruction of water canals. Moreover, stresses must stay below mechanical material limits. Iterative calculations are necessary in order to find optimum between neutronic data, thermal cooling and mechanical effect.
Further studies are foreseen between mechanic/neutronic entities, notably on the MCNP capability for reading unstructured mesh.
 |
Fig. 12 Relative swelling load in P5 triangular sector (fluence effect). |
 |
Fig. 13 Thermal power due to irradiation on P5 sector. |
 |
Fig. 14 Induced relative movement on P5 due to swelling. |
6 Conclusion
In a reactor design, it is mandatory to loop over different physics in order to reach the required performance. At the beginning, because of time calculation and non-obvious geometry, simplified reflector models are requested to define main core structures. At the end of the design, it is very important to be as close as possible to the final geometrical definition, enabling fine calculation in different fields. In this context, this paper shows the methods used in TechnicAtome to answer such problematics and to link physics fields together.
Thanks to MCNP options and computer's performance, it has been possible to precisely describe the JHR reflector model, enabling to compute input data for mechanical studies such as structural swelling. Heterogeneous reflector induces specific feature on structures. For example, a fine mesh on the gamma screen shows an increase of the heating on the interface between the outside shield and the beryllium reflector. Precise physics description is possible with MCNP and enables the user to understand and treat, if needed, local effects.
Another quantities dealt by the industrial is the flux. Local thermal flux distribution is very dependent on the surrounded environment. For instance, high fluctuations close to sector C2 can now be explained and dealt with. However, in a nuclear safety approach, this step has to be confirmed with other codes. Preliminaries works has been undertaken with TRIPOLI-4®.
Further studies are lead to determine all reactor features in terms of safety and design, taking into account physical quantities variation over a cycle for example. Moreover, design studies based on photon induced heating take into account nuclear data bias thanks to high quality experimental qualification performed by CEA.
Author contribution statement
I (Edwin Privas) have done the analysis and Dr Laurent Chabert the verification.
References
- G. Bignan et al., The Jules Horowitz Reactor, A New high Performances European MTR (Material Testing Reactor) with modern experimental capacities: Toward an International Centre of Excellence, Meeting of the International Group on Research Reactors, RRFM 2012 (Prague, Czech Republic, 2012) [Google Scholar]
- P. Console Camprini et al., Power transient analysis of fuel-loaded reflector experimental device in Jules Horowitz Reactor (JHR), Ann. Nucl. Eng. 94, 541 (2016) [CrossRef] [Google Scholar]
- G. Willermoz et al., HORUS3D: A consistent neutronics/thermohydraulics code package for the JHR modeling, in Proc. of ENC, 2002 Lille, France (2002) [Google Scholar]
- T. Goorley et al., Initial MCNP6 release overview, Nucl. Technol. 180, 298 (2012) [Google Scholar]
- L. Chabert et al., Neutronic Design of small reactor, in Proceeding of the 14th International Topical Meeting on Research Reactor and Fuel Management, RRFM 2010, Marrakech (2010) [Google Scholar]
- O. Petit et al., TRIPOLI-4 Version 8 User Guide, Technical Report, SERMA/LTSD/RT/11-5185/A 2013 [Google Scholar]
- J. Leppänen et al., The Serpent Monte Carlo code: status, development and applications in 2013, Ann. Nucl. Eng. 82, 142 (2015) [CrossRef] [Google Scholar]
- J. Allison et al., Geant4 developments and applications, IEEE Trans. Nucl. Sci. 53, 270 (2006) [Google Scholar]
- CSEWG-Collaboration, Evaluated Nuclear Data File ENDF/B-VI.8, http://www.nndc.bnl.gov/endf [Google Scholar]
- H. Grady Hughes, Information on the MCPLIB02 Photon Library, Los Alamos National Laboratory memorandum X-6:HGH-93-77, 1993 [Google Scholar]
- ANSYS® Structural Mechanics, Release 15.0, 2013 [Google Scholar]
Cite this article as: Edwin Privas, Laurent Chabert, Reflector features and physics consideration issued from the Jules Horowitz Reactor design analyses, EPJ Nuclear Sci. Technol. 4, 18 (2018)
All Tables
All Figures
 |
Fig. 1 JHR general description. Sectors name is given within orange boxes. Grey is for beryllium, blue for water, purple for aluminum, turquoise blue for zircaloy and orange for NaK. |
| In the text | |
 |
Fig. 2 Core components description view. Grey is for beryllium, blue for water, purple for aluminum, turquoise blue for zircaloy and orange for NaK. |
| In the text | |
 |
Fig. 3 Weight ponderation scheme on the left and neutron flux weight map obtained with the MCNP generator on the right, for neutron energy from 5 MeV to 20 MeV. |
| In the text | |
 |
Fig. 4 Fine mesh used for distribution map. |
| In the text | |
 |
Fig. 5 Neutron heating on the left and gamma heating on the right. The values are taken in the axial center of the core, integrated axially over 5 cm. Neutron heating in reflector is, by an average factor 5, lower than gamma heating (different color scale). |
| In the text | |
 |
Fig. 6 Total heating in the gamma shield of P1 sector (along × abscise). An increase of the energy deposition is found at the interface with the beryllium. |
| In the text | |
 |
Fig. 7 Photonic spectrum taken at the internal and external gamma shield interface. |
| In the text | |
 |
Fig. 8 Dominant gamma interactions depending on the incident gamma energy and the proton number of the target. |
| In the text | |
 |
Fig. 9 Photonic spectrum taken at the internal and external gamma shield interface. |
| In the text | |
 |
Fig. 10 Thermal flux distribution. Values are taken in the axial center of the core, integrated axially over 5 cm. |
| In the text | |
 |
Fig. 11 Azimuthal flux distribution for a radius of 38.6 cm, close to pressure vessel and crossing mainly water and aluminum structures. |
| In the text | |
 |
Fig. 12 Relative swelling load in P5 triangular sector (fluence effect). |
| In the text | |
 |
Fig. 13 Thermal power due to irradiation on P5 sector. |
| In the text | |
 |
Fig. 14 Induced relative movement on P5 due to swelling. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


